Перейти к:
Оптимизация технических решений при проектировании усиления основания по струйной технологии
https://doi.org/10.37538/2224-9494-2022-3(34)-92-102
Аннотация
Введение. Струйная цементация грунтов с каждым годом становится все более востребованной технологией в строительстве. Для дальнейшего повышения ее эффективности возникает необходимость оптимизации расхода цемента и объемов буровых работ для снижения стоимости работ по усилению основания.
Целью работы является разработка общего подхода, который может быть использован при проектировании для определения оптимальных параметров армирования массива вертикальными грунтоцементными элементами.
Материалы и методы. На основании традиционных подходов был создан и апробирован поисковый алгоритм, построенный на методе покоординатного спуска с использованием специализированного геотехнического программного обеспечения. Решалась задача определения длины и шага армирующих элементов, при котором обеспечивается наперед заданная величина осадок фундаментов, опирающихся на армированный массив. Приведен пример использования выбранного подхода к решению пространственной задачи оптимизации, проиллюстрированный с помощью программного комплекса Plaxis 3D.
Результаты. Применение разработанного подхода при решении конкретной задачи показало принципиальную возможность минимизировать объемы работ с сохранением и/или снижением величины осадки. В рассмотренном частном примере уменьшение суммарной длины грунтоцементных элементов составило 16 % в песчаных грунтах и 8,4 % в глинистых, что на практике является существенным значением.
Выводы. Показано, что в большинстве случаев прикладное решение задачи оптимизации армирования грунтоцементными элементами грунтового массива может быть найдено и реализовано при использовании алгоритма с введением упрощающих предпосылок, унификации шага и длины армоэлементов, что позволит рационально использовать стандартное геотехническое программное обеспечение и даст возможность реализации оптимизированных решений на практике.
Ключевые слова
Для цитирования:
Разводовский Д.Е., Кузина А.А. Оптимизация технических решений при проектировании усиления основания по струйной технологии. Вестник НИЦ «Строительство». 2022;34(3):92-102. https://doi.org/10.37538/2224-9494-2022-3(34)-92-102
For citation:
Razvodovsky D.E., Kuzina A.A. Optimization of technical solutions during the design of base reinforcement using jet grouting. Bulletin of Science and Research Center of Construction. 2022;34(3):92-102. (In Russ.) https://doi.org/10.37538/2224-9494-2022-3(34)-92-102
Введение
В настоящее время работы по армированию оснований, в том числе по струйной технологии, стали неотъемлемой частью устройства фундаментов. При этом на повестку из научной в сугубо практическую плоскость выходит задача оптимизации армирования основания в реальном проектировании, что в итоге дает возможность снижения стоимости строительно-монтажных работ на нулевом цикле.
Задачи оптимизации устройства строительных конструкций стоят на повестке дня уже длительный срок, но в основном в качестве чисто научной проблемы. В области механики грунтов и фундаментостроения этому вопросу посвящены работы Ю.М. Почтмана [1], А.Г. Дорфмана [2] и др. С точки зрения закрепления грунтов наиболее значимыми являются работы научной школы В.А. Ильичева (Г.А. Бобырь [3] и Ю.А. Готман [4]).
Г.А. Бобырь [3] была разработана методика определения оптимальных параметров искусственно преобразованных грунтов с использованием МКЭ в плоской постановке. Для построения поискового алгоритма использовался численный подход к поиску безусловного экстремума нулевого порядка – метод деформируемого многогранника, а для учета ограничений – метод штрафных функций. Работа Ю.А. Готман [4] посвящена оптимальному закреплению грунтов по струйной технологии для уменьшения давления на подпорные конструкции. Решение основано на применении метода проекции градиента для определения оптимального коэффициента жесткости основания в задаче конечномерного оптимального проектирования. Предметом оптимизации является коэффициент жесткости основания, а основные ограничения накладываются на горизонтальные перемещения ограждения котлована. Был составлен алгоритм поиска условного экстремума, позволяющий вычислять оптимальное распределение коэффициента жесткости по высоте ограждения, выявлены особенности взаимодействия грунтоцементного массива с грунтом при экскавации котлована, рассмотрен ряд решений, которые могут иметь не только теоретическое, но и практическое значение.
Отметим, что рассмотренные выше вопросы ставились для задач плоской деформации. Расчету конструкций по струйной технологии посвящено значительное количество работ [5][6][7] и др. Их характерная особенность состоит в том, что они основываются на решении осесимметричной задачи. В настоящее время появилась возможность произвести расчет в трехмерной постановке, используя коммерческие программные продукты.
Постановка задачи
В рамках статьи опишем возможный подход к решению практической задачи оптимизации армирования основания. Условие задачи может быть сформулировано в следующем виде: необходимо определить параметры армирования по струйной технологии грунтового основания при использовании минимального расхода материала, при котором обеспечивается наперед заданная предельная расчетная величина осадки.
Общая длина грунтоцементных элементов является функцией, подлежащей минимизации ΣLгц (L(i), H(i)) → min при обеспечении требуемой величины осадки фундамента, зависящей от инженерно-геологического строения площадки, характеристик здания и способа армирования основания. Параметрами функции, подлежащей оптимизации, являются длина и шаг i-го конструктивного решения армирования.
Основные поисковые алгоритмы теории оптимального проектирования [3][4] и др. построены на идее, заключающейся в том, что путем последовательных изменений оптимизируемых параметров можно прийти к наиболее практичному техническому решению, удовлетворяющему всем требованиям проекта. Ключевой вопрос состоит лишь в максимальном сокращении количества поисковых итераций для получения решения с требуемой точностью. Допустимые решения могут быть найдены методом перебора, но может быть проведена и более рациональная процедура оптимизации, например с использованием подхода, представленного в настоящей статье.
Первым шагом оптимизации является нулевая итерация на основании базового решения, принимаемого с постоянной по глубине и шагу в плане схемой армирования. Предварительное армирование определяется из заранее заданных геометрических размеров сечения армоэлементов и характеристик грунтоцемента в соответствии с [5]. Оно должно удовлетворять всем необходимым ограничениям: усилия и деформации в грунтоцементных элементах, выбранная схема унификации. Следует учитывать, что для решения задачи нужно принимать во внимание имеющиеся объекты-аналоги, инженерный опыт и интуицию, особенно при выборе вариантов унификации зон, где принимаются одинаковая длина и шаг элементов армирования. Это необходимо для перераспределения усилий и сглаживания их значений в конструкциях проектируемого сооружения, что, в свою очередь, положительно влияет на подбор армирования и позволяет предельно упростить задачу, что увеличивает возможность использования результатов на практике.
Дальнейший поиск решения производят методом покоординатного спуска. Наиболее простым способом определения направления спуска является выбор в качестве искомой функции одного из координатных векторов. В нашем расчетном случае искомой функцией является минимизация осадки от величины общей длины армирующих элементов, а координатными векторами – дискретная корректировка длины и шага элементов. Принятая двунаправленная схема варьирования длины позволяет одновременно корректировать как центральные, так и переметральные элементы одновременно, очередность такой корректировки может быть произвольной, но для уменьшения времени процессов оптимизации производится расчет с учетом обеспечения экономии грунтоцемента.
Управление итерационным процессом и общая последовательность расчета может быть осуществлена в ручном режиме. Сначала увеличивается длина центральных элементов, затем производится перерасчет длин крайних элементов так, чтобы общее количество грунтоцемента было ниже базового (начального) значения, и расчетная осадка не превышала предельного значения. При превышении предельного значения расчетной величины осадки увеличивается длина центральных элементов с переходом наследующий шаг и повторяются итерации. Итерационный процесс прекращается, когда значение вертикальных перемещений фундамента при корректировке длины центральных элементов при максимальной допустимой длине периметральных в данной группе итераций превысит предельное значение. В результате многомерный поиск заменяется последовательностью одномерных поисков с минимизацией функции одной переменной.
Предложенная процедура проиллюстрирована на рис. 1. Базовое решение определяет положение Uпр, величину вертикальных деформаций, которую недопустимо превышать. На рис. 1а показано выполнение первого шага оптимизации по длине армоэлементов. Точки одного цвета соответствуют одинаковой длине центральных элементов и итерационной корректировке периметральных. Как только величина осадки превысит значение Uпр, необходимо снова увеличить длину центральных элементов иповторить расчет заново. Таким образом, мы находим множество решений, подходящих для второго шага оптимизации – по шагу периметральных элементов. Далее переходим ко второму шагу оптимизации: убираем из выделенной зоны один грунтоцементный элемент, подбираем новый шаг и производим перерасчет решений. В результате возникают две возможные ситуации, проиллюстрированные на рис. 1б. Может быть два варианта расположения зеленых точек, соответствующих величине осадки после оптимизации по шагу элементов. Если допустимый диапазон осадок превышен, это означает, что решение не удовлетворяет условиям задачи, но если точка лежит в требуемом диапазоне, то мы можем провести второй шаг оптимизации повторноили остановиться, продолжить анализировать данное множество решений и выбрать удовлетворяющий условиям задачи вариант.
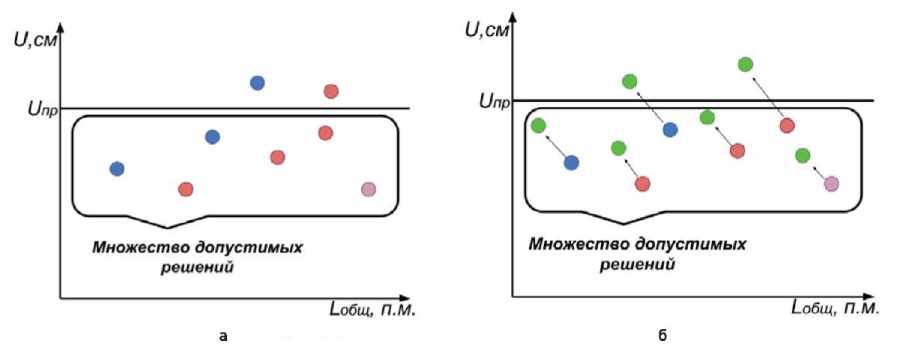
Рис. 1. Порядок проведения оптимизации:
а – оптимизация по длине армоэлемента;
б – оптимизация по шагу армоэлементов
Fig. 1. Optimization procedure:
а – optimization according to the length of the reinforcement element;
б – optimization according to the pitch of reinforcement elements
Реализация решения задачи оптимизации идет в полуавтоматическом режиме. Априори в настоящее время не существует программных средств, позволяющих найти решение задачи, при котором варьируются длины всех элементов при их общем количестве более 25 штук. При этом практически всегда возможно найти локальный минимум целевой функции, введя дополнительные ограничения, что позволяет создать и использовать предложенный ниже подход в реальном проектировании.
Алгоритм метода может быть представлен следующими этапами.
- Выбираем расчетную схему, предварительно задаем способ армирования основания: подбираем длину и шаг армоэлементов, производим их расстановку в плане. Вводим дополнительные ограничения: величину допустимой осадки, устанавливаем диапазон и шаг варьирования длины элементов, предельную прочность элемента усиления.
- Задаем исходную точку поиска U0 (L10, H20), то есть производим базовый расчет, где U0 (L10, H20) – расчетная величина осадки при базовых параметрах длины L10 и шага армоэлементов H20.
- Определяем направление поиска решения: мы можем корректировать параметры L1 и H2 как одновременно, так и дискретно для всего поля армоэлементов или для его частей. Например, для решения задачи может последовательно производиться корректировка сначала длины, а затем и шага армоэлементов.
- Производим первый шаг в направлении оптимизации осадки U1: меняем длину армоэлементов L11 = L10 + λ10e1, где λ10 – длина корректировки длины армоэлемента, а e1 – направление (координатного) спуска, или, простыми словами, направление корректировки (наращивание или подрезка армоэлемента).
Последующая корректировка длины армоэлемента осуществляется с помощью итерационного поиска, завершающегося при достижении граничных условий: превышение величины допустимой осадки, невыполнение условия прочности, геометрические ограничения, наложенные на армоэлементы и др. - После определения положения минимума по параметру L1 делают аналогичный шаг в направлении оптимизации по длине шага армоэлементов H21 = H20 + λ20e2, где λ20 – величина корректировки шага между армоэлементами, а e2 – направление. Аналогично производят итерационный поиск и заканчивают его при достижении других граничных условий: превышение величины шага значений, установленных нормами проектирования, превышение величины допустимой осадки и др.
- После проведения двух последовательных шагов одномерной оптимизации мы получаем решение, которое можно использовать при проектировании.
В указанном выше алгоритме к критериям остановки итерационного процесса были введены дополнительные ограничения на возможность варьирования длинами элементов, вводя в решение наличие групп элементов определенной длины, а также диапазон варьирования длиной элемента. На практике подобные ограничения могут вводиться для обеспечения гарантированного прорезания толщи слабых грунтов.
От общего описания алгоритма решения задачи оптимизации перейдем к порядку действий при проведении расчетов в полуавтоматическом режиме. Существующее программное обеспечение позволяет находить частные решения таких задач, вводя дополнительные ограничения даже без разработки специализированного программного обеспечения, например с использованием Plaxis 3D.
Выполнение расчетов
Расчетная схема задачи для иллюстрации предлагаемого подхода (рис. 2) включает в себя квадратную железобетонную плиту, установленную на армированном основании в толще песчаных грунтов (γ = 23 кН/м2; E = 20 МПа; с = 0 кН/м2; φ = 20°), спромежуточным слоем из щебня. Поле элементов усиления разбито на две зоны: центральные армоэлементы и периметральные (рис. 3) – с целью выравнивания эпюры изгибающих моментов в плите и уменьшения их краевых значений. Принятая схема позволяет производить корректировку длины элементов с шагом 0,25 м (рис. 4), данное значение было принято исходя из практических соображений, его величина варьируется только от требуемой точности расчета.
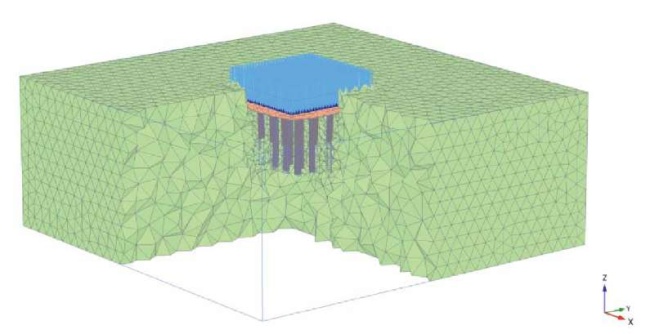
Рис. 2. Принципиальная расчетная схема. Дискретизация сетки конечных элементов
Fig. 2. Schematic design diagram. Discretization of the finite element mesh
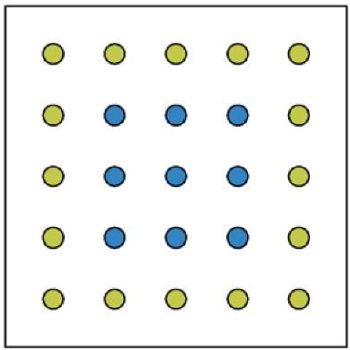
Рис. 3. Схема корректировки длин армоэлементов
Fig. 3. Length adjustment scheme of reinforcing elements
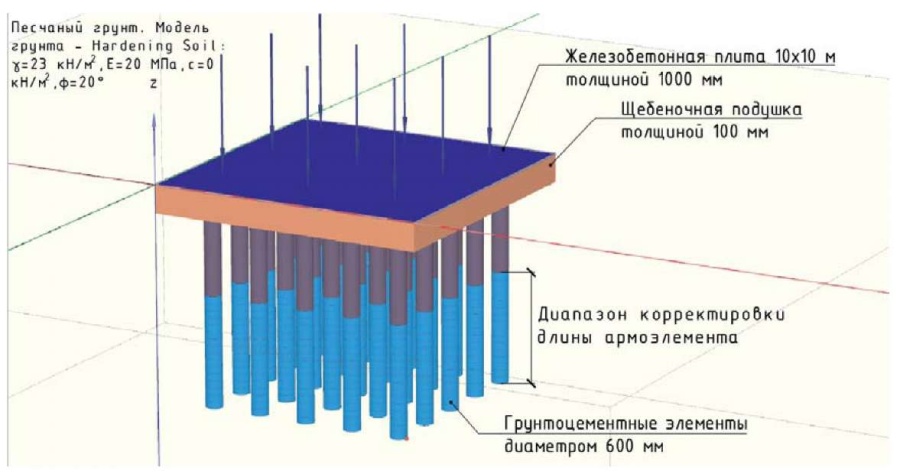
Рис. 4. Детализированная расчетная схема
Fig. 4. Detailed design diagram
Моделирование проводилось с разработкой конечно-элементной дискретизации с возможностью варьирования диапазоном длины армоэлемента в одной разбивки сетки конечных элементов. Преимуществом такого подхода является возможность избежать трудоемкой процедуры перебивки КЭ сетки, что существенно облегчает поставленную задачу.
На первом этапе был выполнен базовый расчет, т. е. нулевая итерация, осуществляемая до проведения процесса оптимизации, и уточнена схема армирования основания с постоянными по длине элементами и шагом. Согласно результатам расчета, величина вертикальных перемещений плиты на армированном основании составила UZ0, что и будет являться значением Uпр для последующей процедуры оптимизации.
Графическое отображение результатов расчета (рис. 5) иллюстрирует результат процедуры одномерной оптимизации. Получившееся множество решений упорядочено в соответствии с количеством требуемого количества грунтоцемента. Зеленым цветом выделены решения, подходящие для второго шага оптимизации, а красным – решения, не выполняющие условия обеспечения предельной осадки.
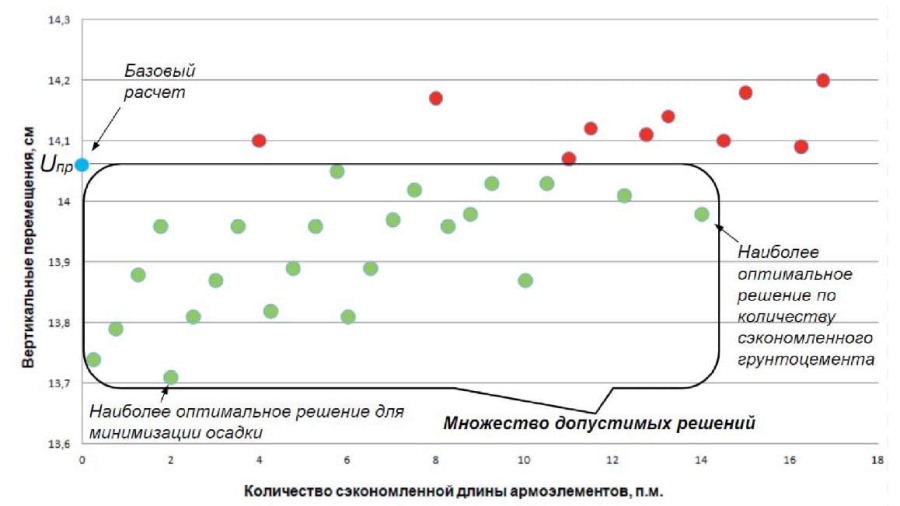
Рис. 5. Вертикальные перемещения плиты в соответствии с количеством сэкономленного грунтоцемента
Fig. 5. Vertical displacements of the plate depending on soil-cement savings
Численно продифференцировав полученное решение, можно найти наиболее экономически выгодный вариант (в количестве использованного грунтоцемента), т. е. условный экстремум, где производная стремится к нулю. Как побочный результат можно выделить решение, при котором обеспечивается минимально возможная величина осадки плиты при обеспечении уменьшения расхода грунтоцемента по сравнению с базовым вариантом.
После проведения первого этапа оптимизации по корректировке длины грунтоцементных элементов производим второй этап оптимизации – по шагу элементов, расположенных по периметру плиты.
Была проведена предварительная процедура оптимизации по шагу элементов для базового расчета в соответствии со схемами на рис. 6. Отметим, что количество вариантов для этого случая априори будет меньшим, поскольку он требует снижения количества элементов, а такое снижение конечно. Было рассмотрено три варианта расположения крайних элементов:
- 16 элементов, шаг установки – 1,8 м (базовый расчет);
- 15 элементов, шаг установки – 1,92 м;
- 14 элементов, шаг установки – 2,05 м.

Рис. 6. Схемы поля армоэлементов для оптимизации по шагу элементов для базового расчета
Fig. 6. Schemes of the reinforcement element field for the element pitch optimization in the basic calculation
Результатом дополнительного расчета являются незначительные увеличения осадки плиты – порядка 1 мм для каждого расчета, следовательно, уменьшение количества грунтоцементных элементов по периметру плиты является допустимым решением оптимизации армированного основания, но лучше использовать данное решение совместно с корректировкой длины грунтоцементных элементов.
Возвращаясь к решениям, полученным в результате процедуры оптимизации по количеству используемого грунтоцемента при корректировке длины элементов, задаем шаг для армоэлементов, расположенных по периметру плиты, в соответствии со схемами на рис. 7 и проводим процедуру оптимизации согласно п. 5 используемого алгоритма.
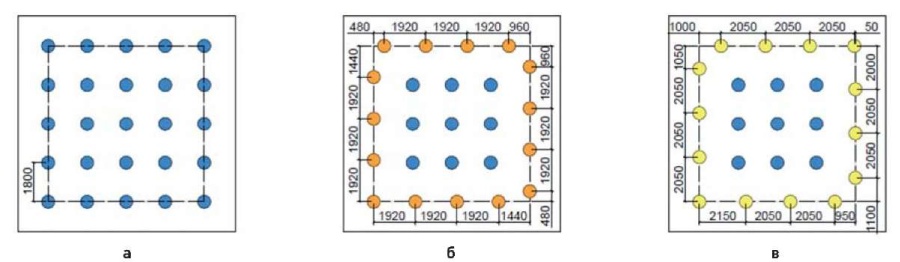
Рис. 7. Схема расположения армоэлементов:
а – базовый расчет (до оптимизации);
б – поле с количеством элементов по контуру, равным 15 шт.;
в – поле с количеством элементов по контуру плиты, равным 14 шт.
Fig. 7. Reinforcement element layout:
а – basic calculation (before optimization);
б – field with 15 elements along the contour;
в – field with 14 elements along the plate contour
Необходимо дополнительно анализировать значение расчетных вертикальных деформаций, так как алгоритм стремится найти параметры длины и шага армоэлементов, при которых значение осадки будет наиболее близко к базовому значению, и пропустить более практичное решение.
В рассматриваемом расчетном случае условно оптимальным является вариант с длиной центральных и крайних армоэлементов, равной 7 и 3,75 м соответственно, и имеющий 15 элементов, расположенных по периметру плиты. Такая компоновка зоны армирования позволяет уменьшить погонную длину применяемых грунтоцементных элементов на 4,6 % от первоначального количества.
Наиболее выгодным вариантом (приближенным к экстремуму) является вариант с длиной центральных и крайних армоэлементов, равной 7 и 3 м соответственно, и имеющий 14 элементов, расположенных по периметру плиты. Этот вариант оптимизации позволяет уменьшить погонную длину применяемых грунтоцементных элементов на 16 % от первоначального количества.
Аналогичная процедура оптимизации проводилась для фундаментной плиты, опирающейся на глинистые грунты (γ = 18 кН/м2; E = 10 МПа; с = 20 кН/м2; φ = 12°). В результате удалось показать возможность сокращения необходимого количества грунтоцемента на 8,4 %.
Выводы
- На современном этапе развития программных средств практическое решение геотехнических задач оптимизации в большинстве случаев может быть найдено лишь при введении упрощающих предпосылок при использовании математического аппарата теории оптимизации. При выборе оптимальной схемы армирования основания отдельными jet-элементами это возможно при введении унификации шага и длины элементов по зонам.
- Оптимизация может осуществляться с использованием традиционных программных средств. В статье показана возможность применения поискового вычислительного алгоритма оптимального проектирования, где предметом оптимизации является осадка и относительная разность осадок, а основные дополнительные ограничения накладываются на диапазон варьирования длин и шага элементов усиления.
- Проведенное численное моделирование с применением упрощенных алгоритмов показало принципиальную возможность минимизировать объемы работ с сохранением и/или понижением величины осадки. В рассмотренном частном примере уменьшение суммарной длины грунтоцементных элементов составило 16 % в песчаных грунтах и 8,4 % – в глинистых, что существенно для практических решений.
Список литературы
1. Почтман Ю.М., Колесниченко А.Л. Методы математической оптимизации в механике грунтов. Киев, Донецк: Вища школа; 1977.
2. Дорфман А.Г., Колесниченко А.Л., Почтман Ю.М., Шевченко М.И. Методы математической оптимизации в механике грунтов. Основания, фундаменты и механика грунтов. 1979;(2):30.
3. Бобырь Г.А. Оптимизация параметров упрочненных массивов в основаниях, сложенных структурно-неустойчивыми грунтами: дис. ... канд. техн. наук. Москва; 2002.
4. Готман Ю.А. Определение оптимальных размеров грунтоцементного массива, снижающего перемещения ограждений глубоких котлованов: дис. ... канд. техн. наук. Москва; 2011.
5. СП 291. 1325800. 2017 Конструкции грунтоцементные армированные. Правила проектирования. Москва: Стандартинформ; 2017.
6. СП 22.13330.2016 Основания зданий и сооружений. Актуализированная редакция СНиП 2.02.01-83* (с Изменениями № 1, 2, 3). Москва: Минстрой России; 2016.
7. Хог Э., Арора Я. Прикладное оптимальное проектирование. Механические системы и конструкции. Москва: Мир; 1983.
8. Singiresu S. Rao. Engineering Optimization.Theory and Practice. New Jersey: John Wiley & Sons; 2009. https://doi.org/10.1002/9780470549124
9. Тер-Мартиросян З.Г., Струнин П.В. Усиление слабых грунтов в основании фундаментных плит с использованием технологии струйной цементации грунта. Вестник МГСУ. 2010;(4-2):310–315.
10. Маковецкий О.А. Расчет и конструирование искусственного основания «структурный геотехнический массив» [диссертация]. Москва; 2021.
11. Малинин А.Г. Струйная цементация грунтов. Москва: Стройиздат; 2010.
Об авторах
Д. Е. РазводовскийРоссия
Дмитрий Евгеньевич Разводовский, канд. техн. наук, заместитель директора по научной работе
109428, г. Москва, Рязанский проспект, д. 59
А. А. Кузина
Россия
Анастасия Андреевна Кузина, инженер
109428, г. Москва, Рязанский проспект, д. 59
Рецензия
Для цитирования:
Разводовский Д.Е., Кузина А.А. Оптимизация технических решений при проектировании усиления основания по струйной технологии. Вестник НИЦ «Строительство». 2022;34(3):92-102. https://doi.org/10.37538/2224-9494-2022-3(34)-92-102
For citation:
Razvodovsky D.E., Kuzina A.A. Optimization of technical solutions during the design of base reinforcement using jet grouting. Bulletin of Science and Research Center of Construction. 2022;34(3):92-102. (In Russ.) https://doi.org/10.37538/2224-9494-2022-3(34)-92-102


























