Перейти к:
О применении жесткостей аналитического метода расчета прямых железобетонных кессонных перекрытий. Часть 2. Расчет с относительной жесткостью балок
https://doi.org/10.37538/2224-9494-2022-4(35)-62-79
Аннотация
Введение. Аналитический расчет железобетонных кессонных перекрытий предусматривает определение составляющих общей нагрузки, приходящихся на балки, в зависимости от величин пролетов и жесткости центральных балок. В случае перекрытий с прямоугольными кессонами, обладающими разной ортогональной жесткостью, данная теория приводит к результатам, значительно отличающимся от расчетов, выполненных методом конечных элементов. Кессонное перекрытие является ребристой плитой, которая характеризуется цилиндрической или относительной балочной жесткостями.
Цель данной работы – выяснение достоверности вычисляемых пролетных изгибающих моментов в балках прямых кессонных железобетонных перекрытий с использованием в формулах аналитического расчета величин пролетов и относительной жесткости балок.
Материалы и методы. Методика выполнения работы предусматривает сравнение изгибающих моментов, полученных аналитическим способом, с данными метода конечных элементов вычислительного комплекса SCAD в балках центральных зон прямых кессонных перекрытий. Рассматривается 13 перекрытий квадратных или прямоугольных в плане с различным соотношением сторон кессонов. В качестве компьютерной модели принята система перекрестных балок из стержней таврового сечения.
Результаты. Максимальные отклонения значений изгибающих моментов, полученных аналитическим методом расчета от компьютерного способа, составляют: для квадратного перекрытия с квадратными кессонами -0,6 %, для квадратного перекрытия с прямоугольными кессонами от -2,8 до +2,5 %, при соотношении пролетов Lmax/Lmin ≤ 1,5 для прямоугольного перекрытия с прямоугольными кессонами от –6,2 до +2,0 %, с квадратными кессонами от –7,3 до +4,8 %. Для прямоугольных перекрытий с любыми кессонами при соотношении пролетов Lmax/Lmin ≥ 1,75 компьютерным расчетом выявлено отклонение эпюры изгибающих моментов длинного направления от параболы.
Выводы. Применение в формулах аналитического метода расчета прямых шарнирно-опертых кессонных железобетонных перекрытий величин пролетов и относительной жесткости балок позволяет получить величины изгибающих моментов, имеющих хорошую сходимость с методом конечных элементов.
Ключевые слова
Для цитирования:
Мозголов М.В., Козлова Е.В. О применении жесткостей аналитического метода расчета прямых железобетонных кессонных перекрытий. Часть 2. Расчет с относительной жесткостью балок. Вестник НИЦ «Строительство». 2022;35(4):62-79. https://doi.org/10.37538/2224-9494-2022-4(35)-62-79
For citation:
Mozgolov M.V., Kozlova E.V. Use of analytical method for calculating stiffnesses of straight waffle slabs. Part 2. Calculation using relative stiffness of beams. Bulletin of Science and Research Center of Construction. 2022;35(4):62-79. (In Russ.) https://doi.org/10.37538/2224-9494-2022-4(35)-62-79
Введение
Данная работа является продолжением изучения аналитического метода расчета прямых кессонных железобетонных перекрытий [1]. Причиной этому стал анализ имеющихся в литературе данных аналитических и компьютерных расчетов кессонных конструкций, который показывает, что в зависимости от созданной конечно-элементной модели и геометрии перекрытия усилия в балках могут существенно отличаться [2–4][16]. Методика выполнения работы предусматривает сравнение усилий – изгибающих моментов, полученных аналитическим способом и методом конечных элементов в вычислительном комплексе SCAD в балках центральных зон прямых кессонных перекрытий с различной геометрией в плане и различным соотношением сторон кессонов. Самой простой и наиболее точной как в расчетном смысле метода конечных элементов [5][6], так и по геометрии пространственной модели для изучения напряженно-деформированного состояния ребер кессонных перекрытий при сравнении с аналитическим методом расчета, основанным на балочной аналогии, будет стержневая конечно-элементная модель со сбором нагрузки на балки по законам треугольника и трапеции. В качестве конечных элементов принят пространственный стержень таврового сечения – тип 5. Известная аналитическая теория расчета железобетонных кессонных конструкций основана на аналогии расчета плит, опертых по контуру [7–13]. На первом этапе расчета определяются составляющие общей нагрузки, приходящиеся на балки qx + qy = q, расположенные вдоль осей X и Y, зависящие только от размеров пролетов перекрытия Lx и Ly. Это свидетельствует о принятии в расчете одинаковых жесткостей отдельных центральных ортогональных балок, или условных выделенных полос, а не жесткостей перекрытия. Поэтому жесткости в формулы не входят, они сокращаются по правилам математики. В первой части работы [1] доказано, что использование жесткости отдельных центральных ортогональных балок в общем случае расчета приводит к неверным результатам. Без учета жесткостей можно рассчитывать только шарнирно-опертые по контуру перекрытия квадратные в плане с квадратными кессонами, так как в данном случае жесткости в формулах сокращаются. Кессонное перекрытие является плитой, опертой по контуру, подкрепленной снизу ребрами жесткости. Плитные конструкции характеризуются цилиндрической жесткостью, относительной балочной жесткостью или их суммой [14]. Поэтому в данной работе в качестве жесткости аналитического метода расчета железобетонных кессонных перекрытий рассматривается относительная жесткость балок по ортогональным направлениям X и Y.
Цель
Целью данной работы является выяснение достоверности получаемых усилий в балках прямых кессонных железобетонных перекрытий с использованием в формулах аналитического расчета относительной жесткости отдельных ортогональных балок, расположенных в центральных зонах перекрытия.
Материалы и методы исследования
На первом этапе известного аналитического расчета [7–13] определяются составляющие общей нагрузки, приходящиеся на балки qx + qy = q, расположенные вдоль осей X и Y, зависящие от размеров пролетов перекрытия Lx и Ly и жесткостей отдельных центральных ортогональных балок Bx и By.
𝐵𝑥 = 𝐸 × 𝐼𝑥, (1)
𝐵𝑦 = 𝐸 × 𝐼𝑦, (2)
где Е – модуль упругости материала;
Ix и Iy – моменты инерции балок вдоль осей X и Y.
 , (3)
, (3)
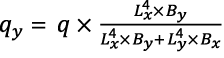 . (4)
. (4)
На втором этапе определяются усилия – изгибающие моменты и поперечные силы.
Максимальные изгибающие моменты в балках, расположенных вдоль осей X и Y, определяются по формулам:
 , (5)
, (5)
 , (6)
, (6)
где α1 и α2 – коэффициенты, зависящие от характера распределения нагрузки и вида опорных закреплений. При равномерно-распределенной нагрузке на перекрытие и шарнирно-опертом контуре α1= α2= 0,125;
a и b – шаг балок;
nx и ny – коэффициенты пропорциональности, зависящие от расположения балок в перекрытии.
В работе [14, с. 410][411] при расчете плит, усиленных симметрично относительно оси плиты ребрами жесткости, жесткость конструкции определяется как сумма, состоящая из цилиндрической жесткости плиты и относительной жесткости ребер:
 , (7)
, (7)
 , (8)
, (8)
где E и E’ – модули упругости материала плиты и ребер;
h – толщина плиты;
ν – коэффициент Пуассона;
I1 и I2 – моменты инерции ребер жесткости вдоль осей X и Y;
b1 и a1 – расстояния между ребрами.
Жесткость плиты Dy , усиленной с одной стороны системой равноотстоящих ребер, определяется по следующей формуле:
 , (9)
, (9)
где E – модуль упругости материала;
I – момент инерции отдельной тавровой балки;
a1 – шаг равноотстоящих балок.
При расчете балочных сеток жесткость по ортогональным направлениям определяется по формулам:
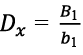 , (10)
, (10)
 , (11)
, (11)
где B1 и B2 – жесткость при изгибе каждой из балок вдоль осей X и Y;
b1 и a1 – шаг балок.
Перепишем формулы расчета железобетонных кессонных перекрытий с учетом относительных жесткостей отдельных ортогональных тавровых балок, равноотстоящих друг от друга.
 , (12)
, (12)
 . (13)
. (13)
Методика выполнения работы предусматривает сравнение усилий – изгибающих моментов, полученных аналитическим способом и методом конечных элементов в вычислительном комплексе SCAD в балках центральных зон прямых кессонных перекрытий с различной геометрией. Рассматриваются шарнирно-опертые по контуру перекрытия квадратные в плане 12,0 × 12,0 м с размерами кессонов 1,5 × 1,5 м, 2,0 × 1,5 м, 2,4 × 1,5 м, 3,0 × 1,5 м, 4,0 × 1,5 м, прямоугольные перекрытия с размерами в плане 12,0 × 15,0 м, 12,0 × 18,0 м, 12,0 × 21,0 м, 12,0 × 24,0 м с квадратными кессонами 1,5 × 1,5 м и прямоугольные перекрытия 12,0 × 15,0 м, 12,0 × 18,0 м, 12,0 × 21,0 м, 12,0 × 24,0 м с прямоугольными кессонами 1,5 × 1,875 м, 1,5 × 2,25 м, 1,5 × 2,625 м, 1,5 × 3,0 м соответственно. Все расчетные схемы имеют балки параллельного направления с одинаковым расстоянием друг от друга. Перекрытия рассчитываются на равномерно-распределенную нагрузку q = 1 Т/м².
В качестве компьютерной модели, как и в первой части работы, принята система перекрестных балок из стержней таврового сечения (конечный элемент тип 5 – пространственный стержень) с непосредственным приложением к ним погонной нагрузки, собираемой с отсеков по законам треугольника и трапеции [11][12]. Во всех схемах сечение пролетных балок принято высотой 500 мм, шириной ребра 250 мм, толщиной полки 80 мм, шириной полки равной шагу балок, бетоном класса B25.
В часторебристом перекрытии для балок одного направления балки другого направления являются для первых ребрами жесткости и в соответствии с требованиями п. 8.1.11 СП 63.13330.2018 «Бетонные и железобетонные конструкции. Основные положения» в расчете мы должны учитывать всю ширину полки.
В соответствии с требованиями п. 6.2.5 СП 430.1325800.2018 «Монолитные конструктивные системы. Правила проектирования» и п. 2.1.1.1. Методического пособия [17] для учета ползучести бетона и наличия трещин при расчете балок компьютерных моделей начальный модуль упругости бетона умножался на коэффициент 0,2 для участков с трещинами (пролетные балки) и 0,3 для участков без трещин (балки опорного контура).
Выполним аналитический расчет в соответствии с теорией, учитывающей относительную жесткость балок Dx и Dy. Жесткость балок Bx и By определена в ВК SCAD.
Квадратное перекрытие с квадратными кессонами (Lx × Ly)
Перекрытие размером в плане 12,0 × 12,0 м с кессонами 1,5 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б1,5Y (рис. 1).
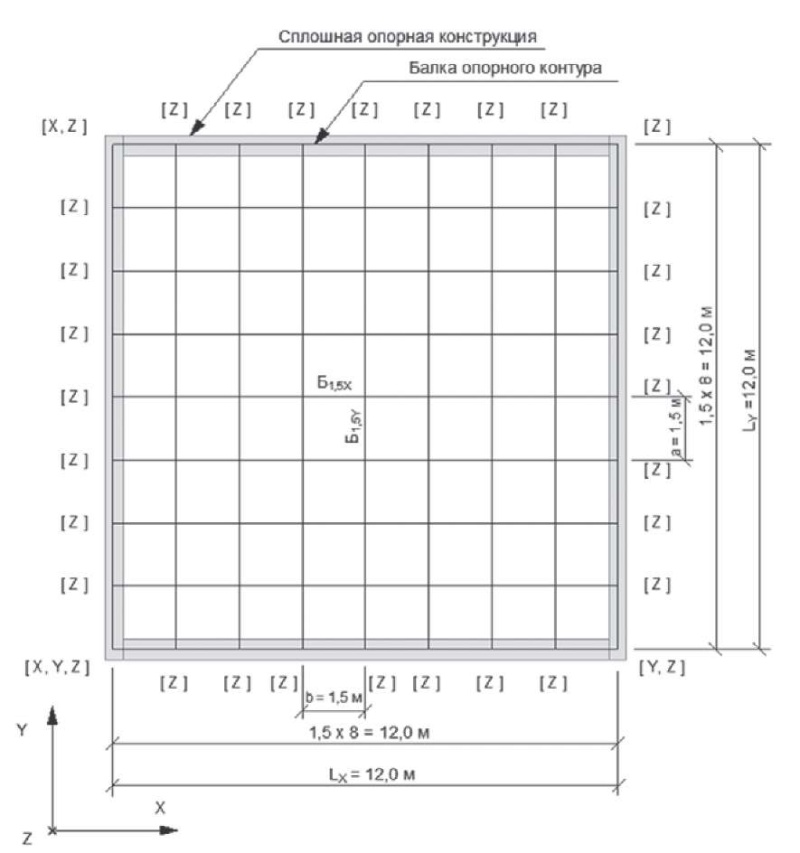
Рис. 1. Схема кессонного перекрытия размером в плане 12,0 × 12,0 м с кессонами 1,5 × 1,5 м.
Б1,5X, Б1,5Y – рассчитываемые балки. [X, Y, Z] – связи, установленные в узлах балки опорного контура
Fig. 1. Schematic of a waffle slab of 12.0 × 12.0 m in plan having 1.5 × 1.5 m coffers.
B1.5X, B1.5Y – calculated beams. [X, Y, Z] – connections established in beam nodes of supporting structure
Относительная жесткость балок:
 , (14)
, (14)
 . (15)
. (15)
Составляющие общей нагрузки, приходящиеся на балки:
 , (16)
, (16)
 . (17)
. (17)
Максимальные изгибающие моменты в середине пролета:
 , (18)
, (18)
 . (19)
. (19)
Квадратные перекрытия с прямоугольными кессонами (Lx × Ly)
Перекрытие размером в плане 12,0 × 12,0 м с кессонами 2,0 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б2,0Y .
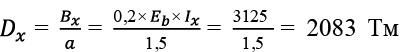 , (20)
, (20)
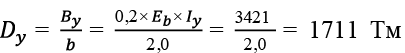 , (21)
, (21)
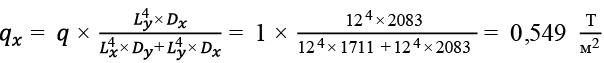 , (22)
, (22)
 , (23)
, (23)
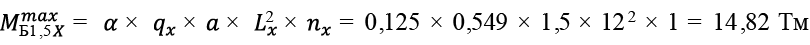 , (24)
, (24)
 . (25)
. (25)
Перекрытие размером в плане 12,0 × 12,0 м с кессонами 2,4 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б2,4Y .
 , (26)
, (26)
 , (27)
, (27)
 , (28)
, (28)
 , (29)
, (29)
 . (30)
. (30)
Коэффициент пропорциональности, учитывающий расположение балки Б2,4Y от опорного контура вдоль оси X.
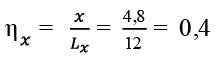 , (31)
, (31)
 , (32)
, (32)
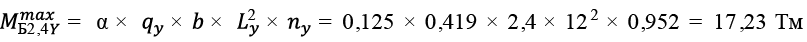 . (33)
. (33)
Перекрытие размером в плане 12,0 × 12,0 м с кессонами 3,0 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б3,0Y .
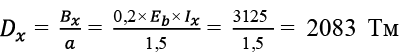 , (34)
, (34)
 , (35)
, (35)
 , (36)
, (36)
 , (37)
, (37)
 , (38)
, (38)
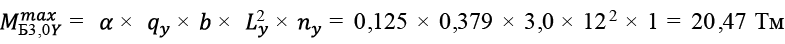 . (39)
. (39)
Перекрытие размером в плане 12,0 × 12,0 м с кессонами 4,0 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б4,0Y .
 , (40)
, (40)
 , (41)
, (41)
 , (42)
, (42)
 , (43)
, (43)
 , (44)
, (44)
 , (45)
, (45)
 , (46)
, (46)
 (47)
(47)
Прямоугольные перекрытия с квадратными кессонами (Lx × Ly)
Перекрытие размером в плане 12,0 × 15,0 м с кессонами 1,5 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б1,5Y .
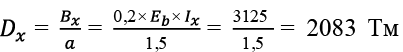 , (48)
, (48)
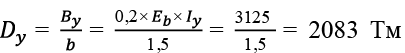 , (49)
, (49)
 , (50)
, (50)
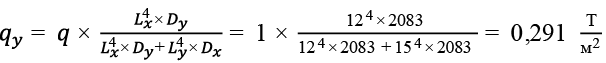 , (51)
, (51)
 , (52)
, (52)
 (53)
(53)
Перекрытие размером в плане 12,0 × 18,0 м с кессонами 1,5 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б1,5Y .
 (54)
(54)
 (55)
(55)
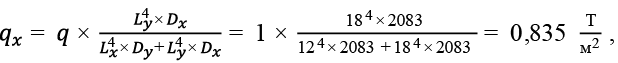 (56)
(56)
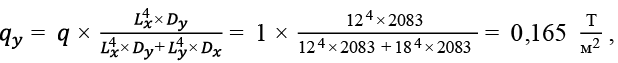 (57)
(57)
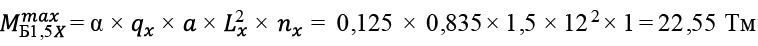 , (58)
, (58)
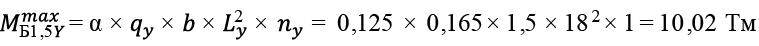 . (59)
. (59)
Перекрытие размером в плане 12,0 × 21,0 м с кессонами 1,5 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б1,5Y .
 (60)
(60)
 (61)
(61)
 (62)
(62)
 , (63)
, (63)
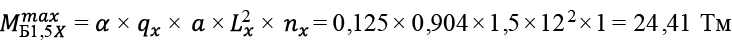 , (64)
, (64)
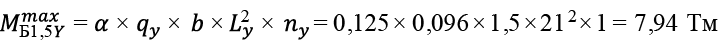 . (65)
. (65)
Перекрытие размером в плане 12,0 × 24,0 м с кессонами 1,5 × 1,5 м. Рассматриваем центральные балки Б1,5X и Б1,5Y .
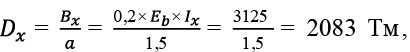 (66)
(66)
 (67)
(67)
 (68)
(68)
 (69)
(69)
 (70)
(70)
 (71)
(71)
Прямоугольные перекрытия с прямоугольными кессонами (Lx × Ly)
Перекрытие размером в плане 12,0 × 15,0 м с кессонами 1,5 × 1,875 м. Рассматриваем центральные балки Б1,875X и Б1,5Y .
 (72)
(72)
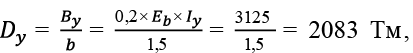 (73)
(73)
 (74)
(74)
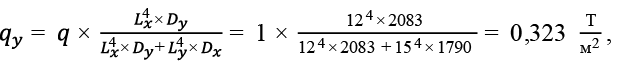 (75)
(75)
 (76)
(76)
 (77)
(77)
Перекрытие размером в плане 12,0 × 18,0 м с кессонами 1,5 × 2,25 м. Рассматриваем центральные балки Б2,25X и Б1,5Y .
 (78)
(78)
 (79)
(79)
 (80)
(80)
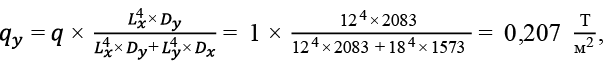 (81)
(81)
 (82)
(82)
 (83)
(83)
Перекрытие размером в плане 12,0 × 21,0 м с кессонами 1,5 × 2,625 м. Рассматриваем центральные балки Б2,625X и Б1,5Y .
 (84)
(84)
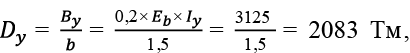 (85)
(85)
 (86)
(86)
 (87)
(87)
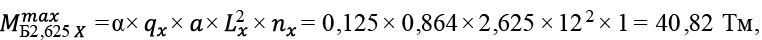 (88)
(88)
 (89)
(89)
Перекрытие размером в плане 12,0 × 24,0 м с кессонами 1,5 × 3,0 м. Рассматриваем центральные балки Б3,0X и Б1,5Y .
 (90)
(90)
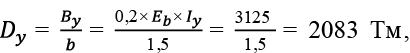 (91)
(91)
 (92)
(92)
 (93)
(93)
 (94)
(94)
 (95)
(95)
Данные аналитического расчета и компьютерных моделей кессонных перекрытий представлены в табл. 1–3.
Результаты
Таблица 1
Сравнение значений изгибающих моментов в балках центральных зон кессонного перекрытия размером в плане (Lx × Ly) 12,0 × 12,0 м с различными размерами кессонов, полученные аналитическим методом и при помощи компьютерных моделей ВКSCAD
Table 1
Comparison of bending moment in central beams of a waffle slab of (Lx × Ly) 12.0 × 12.0 m in plan having different coffer dimensions, obtained by analytical method and computer-assisted calculations using SCAD software
Балка | (1,5 × 1,5 м) Мy, Тм | (2,0 × 1,5 м) Мy, Тм | (2,4 × 1,5 м) Мy, Тм | (3,0 × 1,5 м) Мy, Тм | (4,0 × 1,5 м) Мy, Тм | |||||
Аналитический | SCAD | Аналитический | SCAD | Аналитический | SCAD | Аналитический | SCAD | Аналитический | SCAD | |
Б1,5X | 13,5 99,4 % | 13,58 100 % | 14,82 99,4 % | 14,91 100 % | 15,69 98,4 % | 15,95 100 % | 16,77 100,3 % | 16,72 100 % | 18,14 97,2 % | 18,66 100 % |
Б1,5Y | 13,5 99,4 % | 13,58 100 % | ||||||||
Б2,0Y | 16,24 99,9 % | 16,25 100 % | ||||||||
Б2,4Y | 17,23 100,5 % | 17,14 100 % | ||||||||
Б3,0Y | 20,47 101,6 % | 20,15 100 % | ||||||||
Б4,0Y | 20,52 102,5 % | 20,03 100 % | ||||||||
Таблица 2
Сравнение значений изгибающих моментов в балках центральных зон кессонного перекрытия с размерами кессонов 1,5 × 1,5 м различными пролетами (Lx × Ly), полученные аналитическим методом и при помощи компьютерных моделей ВК SCAD
Table 2
Comparison of bending moment in beams of central waffle slabs having 1.5 × 1.5 m coffer and various spans (Lx × Ly), obtained by analytical method and computer-assisted calculations using SCAD software
Балка | (12,0 × 15,0 м) Мy, Тм | (12,0 × 18,0 м) Мy, Тм | (12,0 × 21,0 м) Мy, Тм | (12,0 × 24,0 м) Мy, Тм | ||||
Аналитический | SCAD | Аналитический | SCAD | Аналитический | SCAD | Аналитический | SCAD | |
Б1,5X | 19,14 95,6 % | 20,02 100 % | 22,55 92,7 % | 24,32 100 % | 24,41 91 % | 26,83 100 % | 25,41 90,3 % | 28,15 100 % |
Б1,5Y | 12,28 101,3 % | 12,12 100 % | 10,02 104,8 % | 9,56 100 % | 7,94 113,4 % | 7,0 100 % 8,33* | 6,37 131,6 % | 4,84 100 % 7,81* |
Примечание: * – В моделях ВК SCAD перекрытий размером 12,0 × 21,0 м и 12,0 × 24,0 м максимальные изгибающие моменты в балках длинной стороны находятся не в середине пролета, эпюра изгибающих моментов не является квадратной параболой. Данный эффект отмечается в работе [15] в плите, опертой по контуру, при соотношении сторон Ly= 2 × Lx
Note: * – In the SCAD software, models of slabs of 12.0 × 21.0 m and 12.0 × 24.0 m, the maximum bending moments in the joists of the long side are off center, the plot of bending moments deflects from the parabola. This effect was observed in the work [15] in a two-way slab at an aspect ratio of Ly = 2 × Lx
Таблица 3
Сравнение значений изгибающих моментов в балках центральных зон кессонного перекрытия прямоугольного плане (Lx × Ly) с прямоугольными кессонами, полученные аналитическим методом и при помощи компьютерных моделей ВК SCAD
Table 3
Comparison of bending moment in central joists of a rectangular-plan waffle slab (Lx × Ly) having rectangular coffers, obtained by analytical method and computer-assisted calculations using SCAD software
Балка | (12,0 × 15,0 м) (1,5 × 1,875 м) Мy, Тм | (12,0 × 18,0 м) (1,5 × 2,25 м) Мy, Тм | (12,0 × 21,0 м) (1,5 × 2,625 м) Мy, Тм | (12,0 × 24,0 м) (1,5 × 3,0 м) Мy, Тм | ||||
Аналитический | SCAD | Аналитический | SCAD | Аналитический | SCAD | Аналитический | SCAD | |
Б1,875X | 22,85 96,2 % | 23,76 100 % | ||||||
Б2,25X | 32,12 93,8 % | 34,24 100 % | ||||||
Б2,625X | 40,82 92,1 % | 44,31 100 % | ||||||
Б3,0X | 49,0 91,2 % | 53,75 100 % | ||||||
Б1,5Y | 13,63 100,9 % | 13,51 100 % | 12,58 102 % | 12,34 100 % | 11,25 104,2 % | 10,8 100 % 11,09* | 10,04 108,8 % | 9,23 100 % 10,46* |
Примечание: * – В моделях ВК SCAD перекрытий размером 12,0 × 21,0 м и 12,0 × 24,0 м максимальные изгибающие моменты в балках длинной стороны находятся не в середине пролета, эпюра изгибающих моментов не является квадратной параболой. Данный эффект отмечается в работе [15] в плите, опертой по контуру, при соотношении сторон Ly= 2 × Lx
Note: * – In the SCAD software, models of slabs of 12.0 × 21.0 m and 12.0 × 24.0 m, the maximum bending moments in the joists of the long side are off center, the plot of bending moments deflects from the parabola. This effect was observed in the work [15] in a two-way slab at an aspect ratio of Ly = 2 × Lx
Кессонные перекрытия с прямыми кессонами эффективно применять при соотношении сторон Lmax /Lmin ≤ 1,5 [3][13]. В формулы определения составляющих общей нагрузки для прямоугольных перекрытий с прямоугольными кессонами входят как разные величины пролетов, так и разные жесткостные характеристики. Это может привести к большей погрешности расчета, поэтому для сравнения полученных усилий представляем расчетную модель ВК SCAD и эпюры изгибающих моментов для перекрытия размером в плане 12,0 × 18,0 м с кессонами 1,5 × 2,25 м (рис. 2, 3).
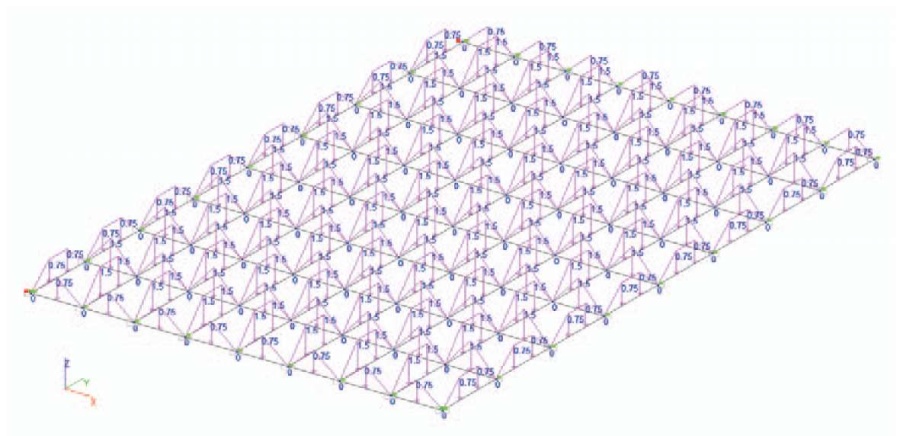
Рис. 2. Расчетная модель SCAD перекрытия размером в плане (Lx × Ly) 12,0 × 18,0 м с кессонами 1,5 × 2,25 м
Fig. 2. SCAD design model of rectangular-plan slab of (Lx × LY) 12.0 × 18.0 m in plan having coffers of 1.5 × 2.25 m
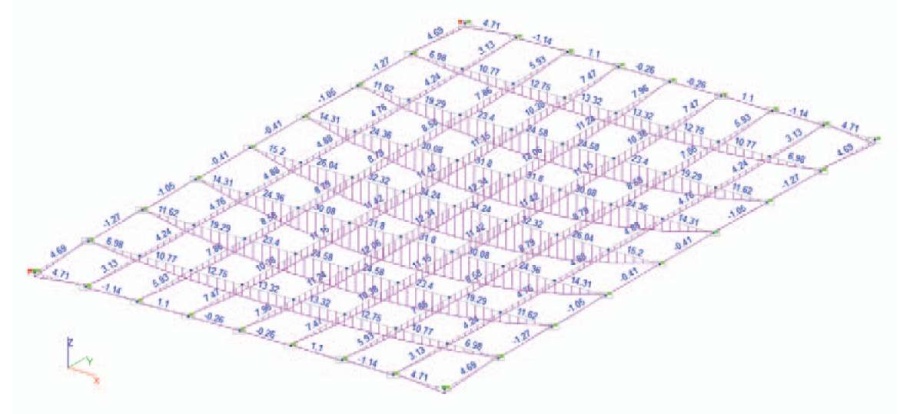
Рис. 3. Эпюры изгибающих моментов Му, Тм, в балках модели SCAD перекрытия размером в плане (Lx × Ly) 12,0 × 18,0 м с кессонами 1,5 × 2,25 м
Fig. 3. Plots of bending moments My, Tm, in joists of SCAD slab model of (Lx × LY) 12.0 × 18.0 m in plan having coffers of 1.5 × 2.25 m
Выводы
- Значения изгибающих моментов в балках перекрытия квадратного в плане с квадратными кессонами, вычисленные аналитическим способом с учетом величин пролетов, относительной жесткости балок и методом конечных элементов вычислительного комплекса SCAD, совпадают. Максимальные отклонения аналитического метода расчета от МКЭ составляют –0,6 %.
- Значения изгибающих моментов в балках перекрытия квадратного в плане с прямоугольными кессонами, вычисленные аналитическим способом с учетом величин пролетов, относительной жесткости балок и методом конечных элементов вычислительного комплекса SCAD, имеют близкие значения. Максимальные отклонения аналитического метода расчета от МКЭ составляют от –2,8 до +2,5 %.
- Значения изгибающих моментов в балках перекрытия прямоугольного в плане с квадратными кессонами и соотношением пролетов Lmax /Lmin ≤ 1,5, вычисленные аналитическим способом с учетом величин пролетов, относительной жесткости балок и методом конечных элементов вычислительного комплекса SCAD, имеют близкие значения. Максимальные отклонения аналитического метода расчета от МКЭ составляют от –7,3 до +4,8 %. Сравнивать значения изгибающих моментов для перекрытия с соотношением пролетов Lmax /Lmin ≥ 1,75 не имеет смысла, так как эпюра изгибающих моментов в большем пролете не соответствует квадратной параболе. Максимальные изгибающие моменты находятся не в середине пролета.
- Значения изгибающих моментов в балках перекрытия прямоугольного в плане с прямоугольными кессонами и соотношением пролетов Lmax /Lmin ≤ 1,5, вычисленные аналитическим способом с учетом величин пролетов, относительной жесткости балок и методом конечных элементов вычислительного комплекса SCAD, имеют близкие значения. Максимальные отклонения аналитического метода расчета от МКЭ составляют от –6,2 до +2,0 %. Сравнивать значения изгибающих моментов для перекрытия с соотношением пролетов Lmax /Lmin ≥ 1,75 не имеет смысла, так как эпюра изгибающих моментов в большем пролете не соответствует квадратной параболе. Максимальные изгибающие моменты находятся не в середине пролета.
- Отклонения по изгибающим моментам аналитического метода расчета от метода конечных элементов можно объяснить влиянием на напряженно-деформированное состояние конструкции перекрытия балки опорного контура и наличием в балках крутящих моментов, не учитываемых аналитическим способом расчета.
- В формулах аналитического метода расчета прямых шарнирно-опертых по контуру ребристых кессонных железобетонных перекрытий при определении составляющих общей нагрузки необходимо использовать величины пролетов и относительную жесткость ортогональных балок. Условием применения данной жесткости является одинаковое расстояние между параллельными балками.
- В связи с тем что стержневая конечно-элементная модель метода конечных элементов является наиболее точной, но не удобной при проектирования здания в целом (нельзя учесть собственный вес конструкций в автоматическом режиме программного комплекса по причине наложения объемов материала, отсутствие данных напряженно-деформированного состояния полки, необходимость ручного расчета погонной нагрузки), дальнейшим исследованием расчета прямых кессонных железобетонных перекрытий может быть моделирование конструкций на ЭВМ с использованием разных типов конечных элементов (плитных, оболочечных, стержневых с применением жестких вставок, объемных, их сочетаний) и сравнение полученных данных с аналитическим методом расчета, учитывающим относительную жесткость балок.
Список литературы
1. Мозголов М.В., Козлова Е.В. О применении жесткостей аналитического метода расчета прямых железобетонных кессонных перекрытий. Вестник НИЦ «Строительство». 2022;33(2):122–138. https://doi.org/10.37538/2224-9494-2022-2(33)-122-138
2. Малахова А.Н. Монолитные кессонные перекрытия зданий. Вестник МГСУ. 2013;(1):79–86.
3. Мозголов М.В., Туранова А.В. Об эффективности косых кессонных железобетонных перекрытий. Градостроительство и архитектура. 2021;11(3):20–25. https://doi.org/10.17673/Vestnik.2021.03.03
4. Шибаева В.Д. Исследование напряженно-деформированного состояния монолитных кессонных перекрытий. Молодой ученый. 2021;(16):119–123.
5. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. Москва: ДМК Пресс; 2007.
6. Мозголов М.В., Козлова Е.В. К вопросу создания верификационной модели для расчета кессонного железобетонного перекрытия в вычислительном комплексе SCAD. Вестник НИЦ «Строительство». 2022;32(1):128–140. https://doi.org/10.37538/2224-9494-2022-1(32)-128-140
7. Залигер Р. Железобетон: его расчет и проектирование. Москва–Ленинград: Изд-во ГНТИ; 1931.
8. Линович Л.Е. Расчет и конструирование частей гражданских зданий. Киев: Будiвельник; 1972.
9. Вахненко П.Ф., Хилобок В.Г., Андрейко Н.Т., Яровой М.Л. Расчет и конструирование частей жилых и общественных зданий: справочник проектировщика. Киев: Будiвельник; 1987.
10. Улицкий И.И., Ривкин С.А., Самолетов М.В., Дыховичный А.А., Френкель М.М., Кретов В.И. Железобетонные конструкции. Киев: Будiвельник; 1972.
11. Иванов-Дятлов И.Г. Железобетонные конструкции. Москва, Ленинград: Министерство коммунального хозяйства РСФСР; 1950.
12. Карпухин Н.С. Железобетонные конструкции. Москва: Государственное издательство литературы по строительству и архитектуре; 1957.
13. Мурашев В.И., Сигалов Э.Е., Байков В.Н. Железобетонные конструкции. Общий курс. Москва: Государственное издательство литературы по строительству, архитектуре и строительным материалам; 1962.
14. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. Москва: Наука; 1966.
15. Бушков В.А. Железобетонные конструкции. II часть. Москва: Стройиздат Наркомстроя; 1941.
16. Лоскутов И.С. Монолитные железобетонные кессонные перекрытия. DWG.ru [Интернет]. Режим доступа: https://dwg.ru/lib/2046 (дата доступа: 24.10.2021).
17. Плоские безбалочные железобетонные перекрытия [Интернет]. Москва; 2017. Режим доступа: https://www.faufcc.ru/upload/methodical_materials/mp60_2017.pdf (дата доступа 22.11.21).
Об авторах
М. В. МозголовРоссия
Михаил Валентинович Мозголов, канд. техн. наук, доцент кафедры «Строительное производство»
Коломенского института (филиала)
ул. Октябрьской революции, д. 408, г. Коломна, 140402
Е. В. Козлова
Россия
Елизавета Вадимовна Козлова, студент 4-го года обучения направления «Строительство» Коломенского института (филиала)
ул. Октябрьской революции, д. 408, г. Коломна, 140402
Рецензия
Для цитирования:
Мозголов М.В., Козлова Е.В. О применении жесткостей аналитического метода расчета прямых железобетонных кессонных перекрытий. Часть 2. Расчет с относительной жесткостью балок. Вестник НИЦ «Строительство». 2022;35(4):62-79. https://doi.org/10.37538/2224-9494-2022-4(35)-62-79
For citation:
Mozgolov M.V., Kozlova E.V. Use of analytical method for calculating stiffnesses of straight waffle slabs. Part 2. Calculation using relative stiffness of beams. Bulletin of Science and Research Center of Construction. 2022;35(4):62-79. (In Russ.) https://doi.org/10.37538/2224-9494-2022-4(35)-62-79


























