Некоторые соображения о построении современной теории расчета железобетонных конструкций

Введение

Касаясь назревших вопросов развития норм по проектированию и производству железобетонных конструкций [1], авторы приводят очевидный факт о том, что действующие нормы базируются в основном на результатах исследований, полученных еще в прошлом веке. Нормы проектирования обычно содержат базу данных о показателях прочностных и деформативных свойств бетона и арматуры, методов расчета конструкций и различных требований (конструктивных, по изготовлению и монтажу и т. д.).

Цель

Несовершенство базы данных достаточно полно рассмотрено в [1]. В данной статье основное внимание уделено вопросу совершенствования теории расчета бетонных и железобетонных конструкций.

Материалы и методы

В соответствии с результатами двухкомпонентной теории ползучести А.А. Гвоздева и К.З. Галустова [2] ниже рассматриваются деформационная и релаксационная задачи компонентов обратимых деформаций ползучести бетона. По определению А.А. Гвоздева, теория расчета только тогда может быть полной, если решены две задачи: деформационная и релаксационная. В настоящее время решение деформационной задачи представлено многочисленными вариантами теории ползучести, опирающимися на многочисленные предпосылки и допущения. Наиболее дискуссионным из них является принцип суперпозиции. Определение внутренних усилий в элементах конструкций осуществляется с помощью методов строительной механики, которые справедливы только для консервативных систем. Конструкции, в которых используется бетон, рассеивают энергию на необратимых деформациях, и система становится неконсервативной. Поэтому существенно важно выделение их из общих деформаций. На это указывал А.А. Гвоздев. Им разработана и впоследствии развита К.З. Галустовым двухкомпонентная теория ползучести, в которой деформации разделены не по признаку упругости и неупругости, а по признаку обратимости. По сути, в ней находятся истоки диссипативной теории ползучести.

Результаты

В 1660 году Р. Гук сформулировал закон, определяющий связь между напряжением и деформацией упругого тела. Тогда и появилось в научной среде понятие о модуле упругости Юнга. Подавляющее большинство научных работ и до настоящего времени используют это понятие в теории железобетона, назвав его модулем упругости или деформаций. Впервые на неупругие свойства бетона обратил внимание А. Консидер (публикация в 1905 г.), то есть на 245 лет позднее. Этот момент можно считать началом рождения науки о ползучести. По молодости своей, по сравнению с теорией упругости, наука о ползучести в общей теории железобетона и сейчас является инструментом для сглаживания расхождений теории и опыта. Заметим, что до настоящего времени все известные теории ползучести не вписаны в существо теории железобетона, а существуют рядом с ней, по крайней мере в нормативных документах. Это привело к тому, что старение бетона определено различными эмпирическими зависимостями для упругости и ползучести. Уравнения состояния, построенные на них, удовлетворяют опыту, но применить их к решению практических задач трудоемко, т. к. они не приводятся к дифференциальным уравнениям, разрешаемым в элементарных функциях. Поэтому стандартным методом решения релаксационных задач в линейной теории ползучести является предварительное определение ядра релаксации, сопряженного с медленно сходящимся рядом [2]. Применение преобразования Лапласа в сочетании с методом малого параметра Пуанкаре, кроме всего прочего, многодельно и труднообозримо.

В 1978 году [3] С.В. Александровский и В.В. Соломонов установили в опытах, что деформации ползучести, удельные по отношению к начальному относительному уровню напряжений η(τ) = σ(τ)/R(τ), практически не зависят от возраста бетона, т. е. инвариантны относительно начала нагружения. Этот замечательный факт долго не был замечен научной общественностью. И только к 1989 году [4] он позволил установить тесную связь между тремя свойствами бетона (прочностью, упругостью и ползучестью). Удалось показать, что у всех компонент напряженно-деформированного состояния бетона (прочности, упругости и ползучести) существует одна общая функция старения, определяемая количеством прогидратированного вяжущего. Полученный результат позволил сформулировать для теории ползучести бетона обыкновенное дифференциальное уравнение (ОДУ) первого порядка, решаемого в элементарных функциях. При этом отпала необходимость многих ограничений, используемых при построении существующих теорий ползучести. Полученное ОДУ позволяет формулировать как задачу определения деформации при заданном режиме напряжения, так и задачу определения напряжения при заданном режиме деформации в элементарных функциях. Покажем это ниже по тексту.

В действующих нормах [5][6] общая мера деформаций бетона или его податливость при одноосном простейшем нагружении представлена в виде:

(1)

где мера ползучести принимается в мультипликативной форме С.В. Александровского и МакГенри, развитой Е.Н. Щербаковым

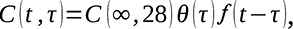(2)

где

(3)

 – функция накопления деформаций ползучести.

Функция старения по [3]

. (4)

Подставив (4) в (1), получим

.

При простом, но разном одноосном сжатии напряжением σ(τ) относительные деформации в момент t

, (5)

где

или

. (5а)

Поскольку причиной деформаций являются напряжения, а (5) оперирует их уровнями согласно [3], то свойства бетона и сами деформации инвариантны относительно времени приложения этих уровней. Тогда скорость деформации

(6)

или

. (6а)

Принципиально важно отметить, что (6) есть дифференциальное уравнение и получено оно так же, как и большинство признанных в теории ползучести средств построения уравнений состояния, например, [7]. Однако в существующих теориях они не могут решаться в элементарных функциях, и это вынуждает применять трудоемкие приближенные способы решения. Наверное, в этом заключается одна из главных причин слабого использования теории ползучести в теории железобетона. В отличие от этого (6) решаемо в элементарных функциях, и этому способствует (4), полученное [4] на основе [3]. Дифференциальное уравнение (6) позволяет построить уравнение деформаций прямым интегрированием

.

Согласно (5), , тогда

,

. (7)

Так может решаться прямая задача теории ползучести при одноосном сжатии бетонных элементов. На практике зачастую требуется решать обратную задачу: по заданным вынужденным деформациям требуется определить уровень напряжения. Это задача о релаксации, которая может быть решена с помощью решения дифференциального уравнения.

Для того чтобы получить классический вид линейного дифференциального уравнения первого порядка [8], имеющего стандартное решение, прибавим к (6) помноженное на γ уравнение (5) и получим

. (8)

Для нахождения общего решения уравнения (8) применяем, как обычно, метод вариации постоянной. Однородное уравнение

является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, имеем

.

Отсюда, потенцируя, находим

или

. (9)

Теперь найдем общее решение уравнения (8) в виде (9), где С будем считать не постоянной, а новой неизвестной функцией от τ (в этом смысл метода), т. е. в виде

. (10)

Чтобы найти функцию С(τ) и, тем самым, решение в виде (10), подставим функцию (10) в уравнение (8). Получим С´(τ) = f(τ)e^τ, а интегрируя, получим

.

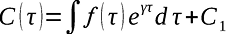Подставляя полученное в соотношение (10), получаем общее решение уравнения (8)

. (11)

Согласно (5)

и тогда

. (12)

Уравнение (11) позволяет определять уровень напряжения в интервале активных вынужденных деформаций t – t₀ .

Если интегрировать уравнение (6а), то получим желаемый результат в другом, но эквивалентном виде

(13)

или

.

Обозначим a = 1 + φ и b = –φke^–γt, подставив их в предыдущее выражение, получим

. (14)

Выводы

Получено решение деформационной и релаксационной задач для центрально сжатого бетонного волокна, представляющего элементарную часть бетонной конструкции с однородными свойствами при центральном сжатии. В природе таких конструкций не существует и, как следствие, для них не существует однородного напряженно-деформированного состояния. Доказательством тому является общепризнанный случайный эксцентриситет. Поэтому теряют корректность расчеты потери устойчивости по Эйлеру как момент достижения конструкцией смены формы равновесия (бифуркации). Не меняется форма равновесия, т. к. не существует центрального сжатия.

Критерий потери устойчивости по А.В. Гиммерлингу, заключающийся в достижении конструкцией нулевой отпорности, эквивалентен достижению предельной несущей способности и сродни предельному равновесию. При этом рассматривается конструкция в целом, т. к. предел может наступить как в результате разрушения одного, так и нескольких элементов. Что станет с остальными элементами – этот непростой вопрос относится к теории прогрессирующего разрушения.

В современной практике в обход упомянутых трудностей используется закон о прямых нормалях. На самом деле он справедлив только тогда, когда в рассматриваемых сечениях конструкции отсутствуют касательные напряжения. В этом случае плоские сечения до деформаций остаются плоскими после деформаций. Это явление имеет строгое доказательство. В связи с отсутствием касательных напряжений в поперечном сечении в силу свойства парности они отсутствуют в продольном сечении. Тогда волокна по высоте сечения следуют закону о прямых нормалях независимо от соседних сверху и снизу волокон. Но ведь это очень редкий случай. Однако такие сечения можно легко найти в любом месте конструкции. Тогда возникает возможность с единых позиций рассматривать напряженно-деформированное состояние (НДС) в случае чистого изгиба, действия поперечной силы, кручения и т. д. Но чтобы поднять этот пласт, следует уже сегодня кардинально пересмотреть сложившиеся отношения к организации научных исследований. Завтра будет поздно.