Перейти к:
Деформирование кладки из крупноформатных камней
https://doi.org/10.37538/2224-9494-2023-2(37)-107-115
EDN: RUQQUT
Аннотация
Введение. Исследуется напряженно-деформированное состояние кладки стен из крупноформатных керамических камней с вертикальными швами «паз-гребень» насухо.
Цель. Исследование картины распределения вертикальных напряжений в кладке из крупноформатных керамических камней с вертикальными швами «паз-гребень», не заполненными раствором.
Материалы и методы. Исследование выполнено на модели участка стены. Численное исследование напряженного состояния кладки фрагмента стены при сосредоточенной нагрузке выполнено для кладки с цепной перевязкой рядов. Фрагмент стены моделировался объемными конечными элементами.
Результаты. Установлено, что под сосредоточенной нагрузкой деформируемая зона имеет вид треугольника с вершиной под нагрузкой и расширяющейся по мере удаления от места приложения нагрузки. На основании проведенных исследований предложен приближенный способ определения напряжений сжатия в камнях кладки с цепной перевязкой рядов. При сосредоточенной нагрузке зона распределения сжимающих напряжений в кладке имеет вид треугольника. Установлены особенности распределения напряжений сжатия в цепной кладке стен из крупноформатных камней с вертикальными швами насухо при сосредоточенной нагрузке.
Выводы. Проведенные исследования показали, что существующие методы расчета сплошной кладки не подходят для расчета кладки с вертикальными швами в «паз-гребень» насухо, потому что последняя представляет собой дискретно-континуальную систему.
Ключевые слова
Для цитирования:
Обозов В.И., Пономарев О.И., Иванова А.Ю. Деформирование кладки из крупноформатных камней. Вестник НИЦ «Строительство». 2023;37(2):107-115. https://doi.org/10.37538/2224-9494-2023-2(37)-107-115. EDN: RUQQUT
For citation:
Obozov V.I., Ponomarev O.I., Ivanova A.Yu. Deformation of large stones masonry. Bulletin of Science and Research Center of Construction. 2023;37(2):107-115. (In Russ.) https://doi.org/10.37538/2224-9494-2023-2(37)-107-115. EDN: RUQQUT
Введение
За последние десятилетия в нашей стране и за рубежом проведено большое количество теоретических и экспериментальных исследований, касающихся оценки напряженно-деформированного состояния кладки стен зданий и сооружений из кирпича и камня, в том числе крупноформатного керамического, с учетом влияния вертикальных швов кладки [1–11], то есть при рассмотрении двухосного напряженного состояния.
Использование такого подхода при построении расчетных моделей предусматривает возможность повышения расчетных нагрузок на конструкции зданий за счет учета работы не только горизонтальных, но и вертикальных швов. Анализ проведенных научных исследований показал, что во всех работах авторы рассматривают кладку из кирпича и камня с полностью заполненными раствором вертикальными швами.
Такая кладка применялась в несущих стенах зданий исторической застройки, в основном в кирпичных зданиях. Однако вертикальный шов кладки из камня в условиях стройплощадки заполнить крайне сложно. Поэтому раствор в вертикальных швах кладки из камня с плоскими вертикальными гранями заполняется не более чем на 20–30 %. В целях исключения продуваемости такие стены возводились с последующим оштукатуриванием двух сторон, а также с облицовкой.
Учитывая большую сложность заполнения раствором вертикальных швов кладки из камня, в последние годы при кладке стен зданий из камня применяются кладочные изделия с пазогребневым соединением вертикальных швов.
Вертикальные швы в такой кладке не заполняются раствором, поэтому между камнями остается зазор в несколько миллиметров. Продуваемость такой кладки значительно меньше, чем в кладке из камней с плоскими вертикальными гранями. Стены из такой кладки также штукатурятся, облицовываются или защищаются наружной системой теплоизоляции.
На рис. 1 показана внутренняя часть стены, возведенная из различных материалов – лицевой кирпичный слой толщиной 0,5 кирпича и основной слой из крупноформатного керамического камня.
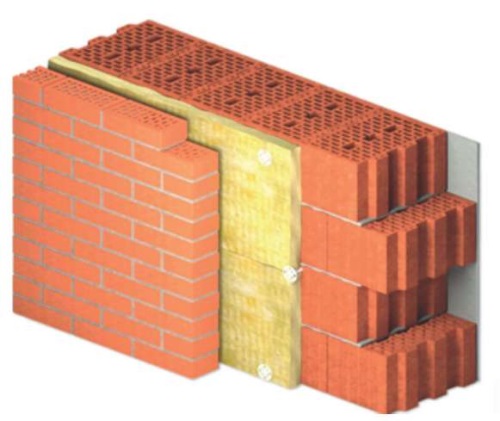
Рис. 1. Пример стены из крупноформатных камней
Fig. 1. Example of large stone masonry wall
В данном случае кладка защищена от внешних температурно-влажностных воздействий лицевым кирпичным слоем и эффективным утеплителем, толщина которого определяется теплотехническим расчетом.
Материалы и методы
Исследования с использованием конечно-элементных моделей
Исследуется напряженно-деформированное состояние кладки несущих стен из крупноформатных керамических камней с вертикальными швами «паз-гребень». Исследовать влияние вертикальных швов «паз-гребень» на напряженно-деформированное состояние кладки под нагрузкой возможно либо экспериментально, либо на компьютерных объемных моделях. Экспериментально влияние не заполненных раствором вертикальных швов (соединение «паз-гребень») возможно сопоставлением результатов испытания образцов кладки двух типов: с заполненными раствором вертикальными швами и с вертикальными швами «паз-гребень» насухо.
Здесь влияние не заполненных раствором швов на напряженно-деформированное состояние кладки из крупноформатных керамических камней исследовано на объемных конечно-элементных моделях фрагментов стен. В [11] разработано два способа построения конечно-элементных объемных моделей:
- прямой метод, когда блоки и растворные швы в модели стены задаются объемными конечными элементами;
- комбинированный метод, когда в модели стены блоки задаются объемными конечными элементами, а растворные швы – пластинчатыми конечными элементами.
Для исследования кладки стен с вертикальными швами между блоками «паз-гребень» насухо использован прямой метод моделирования кладки фрагмента стены. При этом толщина вертикального зазора блоков в кладке принята равной 1 см. В программных комплексах для расчета конечно-элементных моделей используется метод перемещений, поэтому нельзя задавать жесткость КЭ равной 0. В исследованных моделях модуль деформации условного раствора в вертикальных швах был задан равным 1. По сравнению с модулем деформации материала керамических блоков это 0. Поскольку керамические блоки имеют большое количество вертикальных пустот, учитывалось приведенное значение модуля деформации материала блоков равное 15000 кГс/см2. В горизонтальных швах кладки в моделях фрагмента стены был принят раствор марки 100.
Конечно-элементная модель фрагмента стены рассчитывалась на сосредоточенную нагрузку.
Граничные условия были приняты следующими: боковые вертикальные и верхняя горизонтальная грань стены считались свободными без наложенных связей. В нижней опорной грани на узлы конечных элементов были наложены связи, препятствующие перемещениям вдоль координатных осей Х, Y, Z. Общий вид модели приведен на рис. 2.

Рис. 2. Конечно-элементная модель фрагмента стены из крупноформатных керамических камней
Fig. 2. Finite-element model of a fragment of large stone masonry wall
Расчет такой модели на сосредоточенную нагрузку выполнен в двух вариантах: с заполненными раствором вертикальными швами между блоками, когда вертикальные швы раствором не заполнены. Анализ результатов этих расчетов показал, что характер распределения напряжений этих вариантов отличается незначительно. Количественно же, например, вертикальные сжимающие напряжения в варианте с незаполненными вертикальными швами несколько выше.
С целью получения картины распределения вертикальных напряжений в кладке только от внешней нагрузки были произведены дополнительные расчеты этих моделей с невесомыми материалами кладки. Расчеты модели фрагмента стены были произведены с незаполненными раствором вертикальными швами на сосредоточенную вертикальную нагрузку (рис. 3) и с заполненными вертикальными швами (рис. 4). На рис. 3 и 4 приведены изополя вертикальных напряжений в кладке Nz. В обоих случаях четко просматривается зона распределения вертикальных сжимающих напряжений в виде треугольника с вершиной в точке приложения сосредоточенной нагрузки. При этом наблюдается уменьшение напряжений с удалением от места приложения нагрузки и к боковым граням зоны распространения вертикальных напряжений от нагрузки.
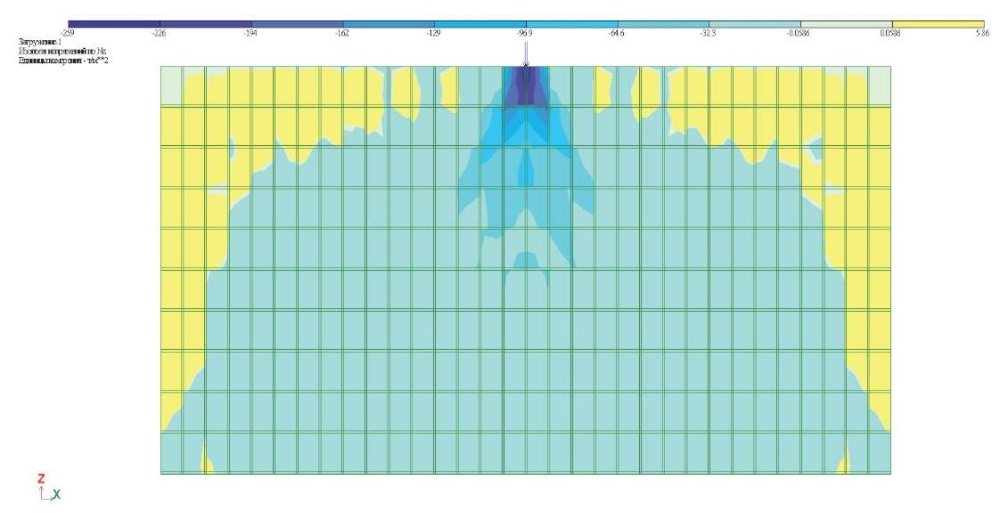
Рис. 3. Распределение вертикальных напряжений при незаполненных вертикальных швах
Fig. 3. Distribution of vertical stresses in dry vertical joints
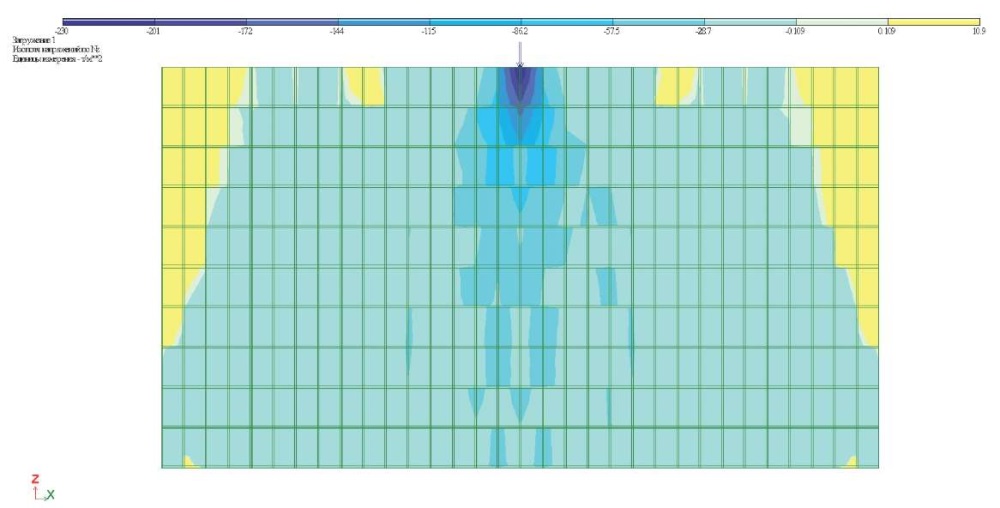
Рис. 4. Распределение вертикальных напряжений при заполненных вертикальных швах
Fig. 4. Distribution of vertical stresses in mortar vertical joints
Угол треугольной зоны распространения сжимающих напряжений в кладке определяется размером блока. Если обозначить высоту блока через h, а больший размер блока через 2l, то угол зоны распространения вертикальных сжимающих напряжений будет равен tgφ = h/l.
Приближенный способ определения напряжений сжатия в камнях кладки со стыками «паз-гребень»
Кладка стен из крупноформатных керамических камней с вертикальными швами в «паз-гребень» насухо представляет собой дискретно-континуальную систему, в которой ряды блоков являются дискретными, а континуальность кладки обеспечивают горизонтальные растворные швы.
Если пренебречь влиянием горизонтальных растворных швов, то можно расписать значения вертикальных сжимающих напряжений блоков в долях от сосредоточенной нагрузки Р в пределах треугольной зоны с углом 2φ в вершине треугольника.
Рассмотрим случай цепной кладки из блоков в один камень. Будем считать, что усилия с каждого блока передаются на два блока, расположенных под ним. Значения усилий в долях от сосредоточенной нагрузки Р в виде дроби в блоках треугольной зоны приведены на рис. 5.
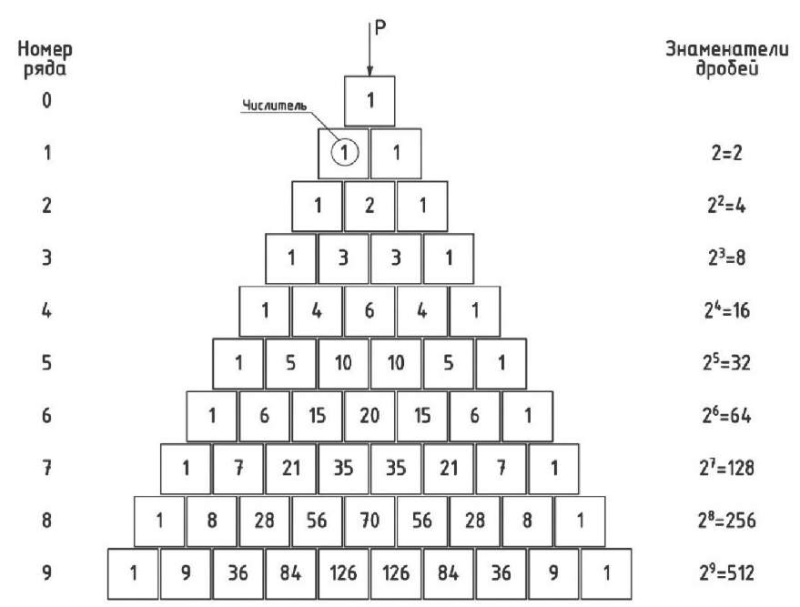
Рис. 5. Треугольник распределения вертикальных усилий в камнях кладки
Fig. 5. Vertical force distribution triangle in masonry stones
Значение усилия, приходящегося на каждый блок, записано в виде дроби. Чтобы получить напряжения, эти усилия необходимо разделить на площадь опорной грани блока. Треугольник, составленный из значений усилий в блоках, обладает некоторыми свойствами. Так, если пронумеровать ряды кладки от нуля (ряд кладки, к которому приложена сосредоточенная нагрузка) с возрастанием номера по мере удаления рядов от нагруженного, то знаменатель в дробях значений усилий представляет собой число 2 в степени, равной номеру ряда. На рис. 5 нанесены только числители дробных значений усилий.
Кроме того, у окаймляющих треугольную зону блоков во всех рядах в числителях дробей усилий стоит 1. Числители усилий в блоках, примыкающих к крайним камням треугольной зоны, равны номерам ряда, считая сверху вниз.
Анализ построенного треугольника усилий в блоках, попадающих в треугольную зону, показал, что вдоль ряда камней они переменны: наименьшие по краям и максимальные на вертикальной оси, проходящей через приложенную сосредоточенную нагрузку. Сумма числителей дробных чисел усилий в пределах ряда равна знаменателю этих дробей.
Полные значения напряжений в камнях определяются как сумма напряжений от нагрузки и напряжений от собственного веса кладки.
Результаты
Проведенные исследования с помощью объемного моделирования фрагмента кладки из керамических камней и растворных швов показали:
- распределение напряжений в кладке из керамических камней с заполненными раствором вертикальными швами и со швами «паз-гребень» насухо качественно совпадает;
- напряжения в камнях кладки со швами «паз-гребень» насухо несколько выше, чем в кладке с заполненными раствором вертикальными швами, которые способствуют большему перераспределению усилий при сосредоточенных нагрузках;
- по схеме статической работы элементов кладки из керамических камней с вертикальными швами «паз-гребень» насухо, кладка может быть отнесена к дискретно-континуальной системе, где дискретными элементами являются камни, а горизонтальные растворные швы вносят эффект континуальности;
- получен треугольник распределения усилий между камнями от сосредоточенной нагрузки на кладку, позволяющий без расчета определять напряжения в камнях кладки с вертикальными швами в «паз-гребень».
Выводы
Проведенные исследования показали, что существующие методы расчета сплошной кладки не подходят для расчета кладки с вертикальными швами в «паз-гребень» насухо.
Список литературы
1. ГОСТ 530-2012. Кирпич и камень керамические. Общие технические условия. Москва: Издательство стандартов; 2012.
2. Баранова Т.И., Ласьков Н.Н, Артюшин Д.В. Сопротивление стен каменной кладки при совместном действии вертикальных и горизонтальных сил. Москва: БСТ; 1998.
3. Баранова Т.И., Туманов А.В. Метод расчета кирпичных и армокирпичных стен на основе стержневых моделей. Промышленное и гражданское строительство. 2001;(8):29–31.
4. Брусенцов Г.И., Будрейка В.Э. Экспериментально-теоретические исследования фрагментов каменной кладки при плоском напряженном состоянии. В: Исследования и методы расчета строительных конструкций. Сб. науч. тр. Москва: ЦНИИСК им. В.А. Кучеренко; 1985, c. 94–101.
5. Гениев Г.А., Воронов А.Н. О критериях прочности ортотропного материала типа каменной кладки при плоском напряженном состоянии. В: Исследования и методы расчета строительных конструкций. Москва: ЦНИИСК им. В.А. Кучеренко; 1985, с. 23–29.
6. Гениев Г.А., Курбатов А.С., Самедов Ф.А. Вопросы прочности и пластичности анизотропных материалов. Москва: Интербрук; 1993.
7. Донченко О.М., Дегтев И.А. К развитию теории трещиностойкости и сопротивления при сжатии. Известия вузов. Строительство. 2000;(10):16–20.
8. Камейко В.А., Ломова Л.М. Исследования кладки из пустотелых керамических блоков. В: Теоретические и экспериментальные исследования каменных конструкций. Сборник трудов ЦНИИСК им. В.А. Кучеренко; Москва: Стройиздат; 1982, с. 37–50.
9. Пангаев В.В. Разрушение сжатой каменной кладки. Изв. Вузов. Строительство. 2000;(12):7–12.
10. Поляков С.В., Чигрин С.И. производство и применение индустриальных керамических панелей. Москва: Стройиздат; 1990.
11. Обозов В.И. Методы построения объемных компьютерных моделей заполнения наружных стен каркасных зданий кладкой из крупных блоков. Строительная механика и расчет сооружений. 2018;(2):50–55.
Об авторах
В. И. ОбозовРоссия
Владимир Иванович Обозов, д-р техн. наук, профессор, заведующий сектором лаборатории кирпичных, блочных и панельных зданий (№ 7)
2-я Институтская ул., д. 6, к. 1, г. Москва, 109428
тел.: +7 (499) 174-77-91
О. И. Пономарев
Россия
Олег Иванович Пономарев, канд. техн. наук, заведующий лабораторией кирпичных, блочных и панельных зданий (№ 7)
2-я Институтская ул., д. 6, к. 1, г. Москва, 109428
тел.: +7 (499) 170-10-59
А. Ю. Иванова
Россия
Александра Юрьевна Иванова, инженер лаборатории кирпичных, блочных и панельных зданий (№ 7)
2-я Институтская ул., д. 6, к. 1, г. Москва, 109428
тел.: +7 (499) 170-10-88
Рецензия
Для цитирования:
Обозов В.И., Пономарев О.И., Иванова А.Ю. Деформирование кладки из крупноформатных камней. Вестник НИЦ «Строительство». 2023;37(2):107-115. https://doi.org/10.37538/2224-9494-2023-2(37)-107-115. EDN: RUQQUT
For citation:
Obozov V.I., Ponomarev O.I., Ivanova A.Yu. Deformation of large stones masonry. Bulletin of Science and Research Center of Construction. 2023;37(2):107-115. (In Russ.) https://doi.org/10.37538/2224-9494-2023-2(37)-107-115. EDN: RUQQUT


























