Перейти к:
Интегральные уравнения второго рода в задачах расчета нелинейных систем с конечным числом степеней свободы при произвольных динамических воздействиях и характере физических зависимостей
https://doi.org/10.37538/2224-9494-2023-3(38)-155-167
EDN: YGYKIE
Аннотация
Введение. Разработка методов расчета нелинейных систем является актуальной областью исследования в связи с тем, что линейная теория не всегда позволяет достоверно описать свойства динамических систем, а для целого ряда случаев линейное приближение дает лишь очень грубое представление о рассматриваемых процессах.
Цель. При расчете линейных систем и записи разрешающих уравнений для нелинейных систем используются передаточные и импульсные переходные функции линейных «порождающих» систем дифференциальных уравнений. Подобный подход по сравнению с традиционным методом «нормальных форм» позволяет значительно упростить алгоритм расчета, исключив из него несколько этапов и представить решение в виде разложения по формам собственных колебаний линейных систем непосредственно относительно обобщенных координат.
Материалы и методы. В статье приведен разработанный метод и алгоритм расчета нелинейных систем с конечным числом степеней свободы при произвольных динамических воздействиях и характере физической нелинейности. В качестве разрешающих уравнений рассматриваются нелинейные интегральные уравнения второго рода, к которым сводятся системы нелинейных дифференциальных уравнений колебаний. Решение строится шагами по времени, величина которого в том числе определяет точность решения и характер численного алгоритма.
Результаты. Основные расчетные зависимости представлены в статье в обобщенном виде и удобны для численного моделирования. Приводятся решения для нелинейной системы с одной степенью свободы при кубической зависимости «реакция–перемещение» и системы с одной и двумя степенями свободы с демпфером вязкого трения. В обоих случаях построенное решение содержит все особенности нелинейных систем. В частности, скачок (переход) с верхней возрастающей ветви на нижнюю, устойчивую, и связанное с этим возбуждение свободных колебаний.
Выводы. Как показали результаты расчетов, возникновение в колебательных системах нелинейных эффектов весьма положительно сказывается на поведении динамических систем, в частности, в резонансных режимах.
Ключевые слова
Для цитирования:
Чернов Ю.Т. Интегральные уравнения второго рода в задачах расчета нелинейных систем с конечным числом степеней свободы при произвольных динамических воздействиях и характере физических зависимостей. Вестник НИЦ «Строительство». 2023;38(3):155-167. https://doi.org/10.37538/2224-9494-2023-3(38)-155-167. EDN: YGYKIE
For citation:
Chernov Yu.T. Integral equations of the second kind in dynamic analysis of nonlinear systems with a finite number of degrees of freedom under arbitrary dynamic loading and material dependencies. Bulletin of Science and Research Center of Construction. 2023;38(3):155-167. (In Russ.) https://doi.org/10.37538/2224-9494-2023-3(38)-155-167. EDN: YGYKIE
Введение
Методы исследования нелинейных колебаний систем, связанные с преобразованием нелинейных уравнений движения систем с конечным числом степеней свободы к нелинейным интегральным уравнениям второго рода, достаточно широко распространены в научно-технической литературе [1–3]. В основном речь идет о построении амплитудно-частотных характеристик (АЧХ) и их анализе.
Между тем, воспользовавшись импульсными переходными функциями (ИПФ) исходных линейных «порождающих» уравнений, нелинейные дифференциальные уравнения могут быть записаны в виде систем нелинейных интегральных уравнений второго рода, которые, по существу, и определяют полное решение исходной системы в виде суммы двух интегралов типа свертки. Один из возможных алгоритмов вычисления подобных интегралов дан, в частности, в статье [4].
При построении решений системы линейных «порождающих» уравнений колебаний использовались фундаментальные зависимости для линейных систем общего вида, приведенные в [5], и несколько более детально для систем с конечным числом степеней свободы в [3].
Общая схема и алгоритм расчета нелинейных систем с конечным числом степеней свободы проиллюстрированы на примере расчета системы с двумя степенями свободы (рис. 1).
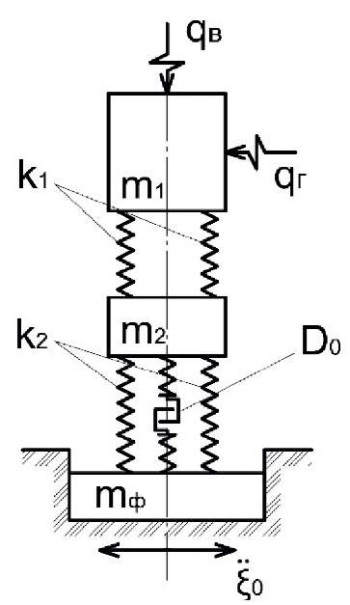
Рис. 1. Расчетная схема системы с двумя степенями свободы:
ki – жесткости связей; D0 – демпфер вязкого трения
Fig. 1. Computational scheme of a system with two degrees of freedom:
ki – bracing stiffness; D0 – viscous damper
Сходимость, устойчивость и точность решений нелинейных систем, построенных используя, в частности, принятый в статье алгоритм, оценивались по результатам расчета двух нелинейных систем с одной степенью свободы.
Стоит отметить, что принятая расчетная схема достаточно широко используется при расчетах различных типов виброзащитных систем: виброизоляции, динамических гасителей колебаний и т. п. – с линейными и нелинейными характеристиками. Подобный алгоритм позволил записать решения линейных уравнений практически в замкнутом виде [2] и в качестве второго примера – решение уравнений плоских горизонтально-вращательных колебаний массивных тел (фундаментов), в том числе заглубленных в грунт [1] (рис. 2).
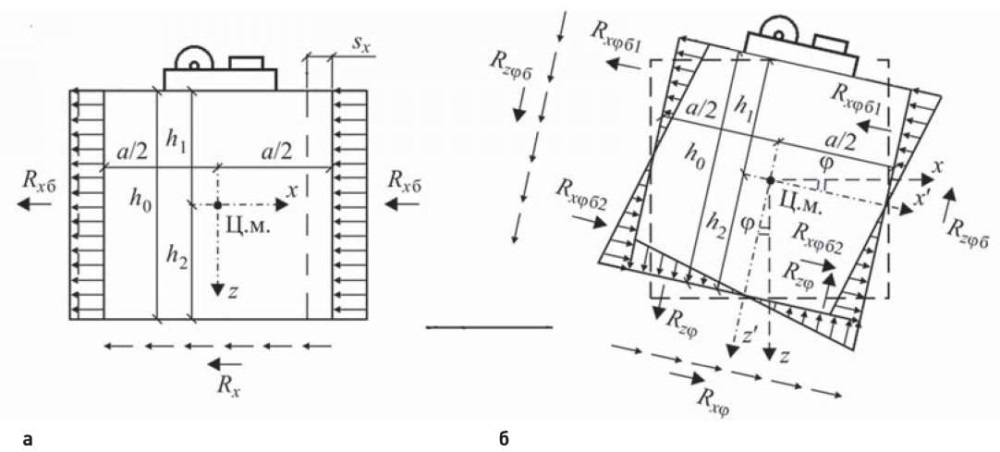
Рис. 2. Реакции в системе «фундамент-грунт» при горизонтальных (а)
и вращательных (б) колебаниях
Fig. 2. Reactions in the “foundation-soil” system under horizontal (a)
and rotational (б) oscillations
Материалы и методы
Процесс построения полного алгоритма расчета нелинейных систем с конечным числом степеней свободы можно разделить на несколько этапов.
На начальном этапе дифференциальные уравнения колебаний систем при нелинейной зависимости «жесткость–перемещение» следует представить в виде (1), записав нелинейные составляющие в правой части:
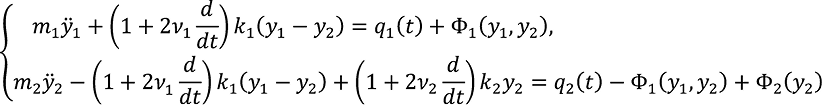 ; (1)
; (1)
где для дальнейшего сокращения записей обозначено:
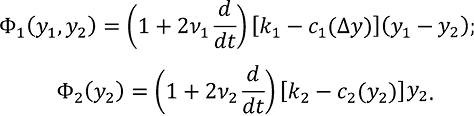 (2)
(2)
k1, k2 – жесткости упругих связей;
v1, v2 – коэффициент затухания в упругих связях;
Δy = y1 − y2.
Передаточные (ПФ) и импульсные переходные (ИПФ) функции этой системы определяют вид интегральных уравнений, которые, по существу, и являются решением системы нелинейных дифференциальных уравнений. Значение этих функций вычисляют из расчета линейной («порождающей») системы уравнений при:
qi(t) = Qieiωt – силовых;
qi(t) = – 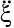 0 Meiωt – кинематических воздействиях.(3)
0 Meiωt – кинематических воздействиях.(3)
где Qi – амплитудные значения усилий;
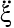 0 – закон смещения основания;
0 – закон смещения основания;
ω – частота вынужденных колебаний.
В матричном виде эту систему следует записать так:
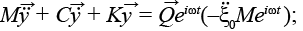 (4)
(4)
где
M = 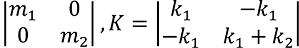 (5)
(5)
– матрицы масс и жесткости.
Используя известные зависимости [2][5], решения подобных систем могут быть представлены в виде разложения по формам собственных колебаний при том, что каждая составляющая полного решения определяется из решения систем уравнений – по структуре систем с одной степенью свободы, диссипативные силы в которых можно учесть, добавив в каждое из них дополнительные слагаемые пропорциональные скорости колебаний.
В работе, в частности, используется модифицированная модель Фойгта с основным параметром γ – коэффициентом неупругого сопротивления. Такая модель принята во многих нормативных документах [6][7], где приводятся также значения этого параметра для различных материалов и сред.
Подобная схема построения алгоритмов расчета более детально дана на примере расчета системы (1).
Следующий этап расчета – вычисление ПФ и ИПФ системы линейных уравнений (4).
Следуя общей схеме вычисления передаточных функций линейной системы [2], подставим в (4):
y→ = Y→eiωt = Q→H→eiωt – при силовом и
y→к = Y→кeiωt = – 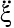 0 MH→eiωt – при кинематическом воздействии,
0 MH→eiωt – при кинематическом воздействии,
где H→– передаточная функция, и, после сокращения на eiωt, запишем систему уравнений относительно элементов вектора Y→:
[(1 + iω2v1)k1 – m1ω2]Y1 – (1 + iω2v1)k1Y2 = Q1;
− (1 + iω2v1)k1Y1 + [(1 + iω2v1)k1 + (1 + iω2v2)k2 – m2ω2]Y2 = Q2.
Из решения которой следует:
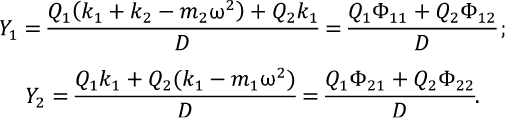 (7)
(7)
где Φij – приближенная (без учета диссипативных сил) амплитуда перемещений i-й массы при действии единичной силы 1 × eiωt на j-ю массу;
D – определитель системы (4), который для сокращения выкладок удобно после некоторых преобразований записать в виде:
 (8)
(8)
где
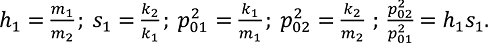 (9)
(9)
Полагая в (8) ω = p и приравняв определитель к нулю, вычислим корни частотного уравнения (значения собственных частот) по формуле:
 (10)
(10)
где φ1 = h1 + h1s1 + 1.
Следуя общей схеме построения ПФ [3][5], определитель системы (4) и его производную по ω2 запишем в виде:
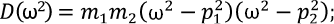 (11)
(11)
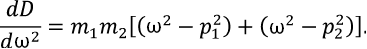 (12)
(12)
Общий алгоритм вычисления передаточных функций можно показать на примере системы (4). Для этого формулу для ПФ, записанную в виде
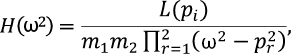 (a)
(a)
где L(pi) – некоторая функция частоты.
Следует преобразовать и представить как сумму отдельных составляющих:
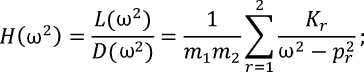 (б)
(б)
где pr – корни уравнения (8) (частоты собственных колебаний), т. е., по существу, в виде разложения по формам собственных колебаний «порождающей» системы, в которой коэффициенты Kr, следуя известной схеме [2], следует определять по формуле:
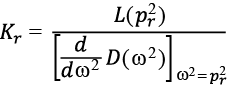 (в)
(в)
Из (б) и (в) следуют общие зависимости для передаточных функций системы (4) также в виде разложения по формам собственных колебаний
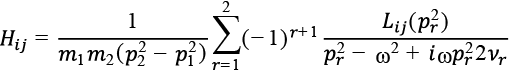 , (13)
, (13)
где
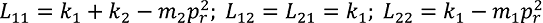 . (14)
. (14)
Последнее слагаемое в знаменателе в (13) позволяет учитывать диссипативные силы, используя наиболее подходящие для конкретных задач модели. Ранее уже было сказано, что в работе далее используется модифицированная гипотеза Фойгта при 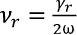 .
.
Передаточные и импульсные переходные функции для общих случаев линейных систем определены в [2].
Для систем с конечным числом степеней свободы алгоритм расчета ИПФ можно несколько упростить, если учесть, что ПФ подобных систем определяются в виде суммы решений систем уравнений по форме систем с одной степенью свободы. В частности, для
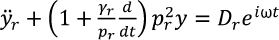 ,
,
при r = 1...n, (15)
где Dr – некоторая функция частоты pr.
ИПФ уравнения (15) удобно записать, воспользовавшись одним из решений для свободных колебаний 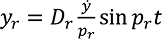 и теоремой сохранения количества движения S = my·, в окончательном виде так
и теоремой сохранения количества движения S = my·, в окончательном виде так
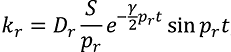 . (16)
. (16)
Из (13) и (16) следуют такие общие зависимости для ИПФ системы (4)
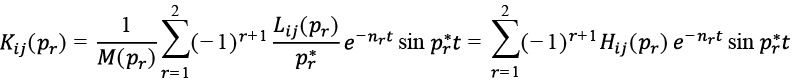 , (17)
, (17)
где
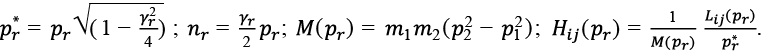 (18)
(18)
Определив ИПФ из решения системы линейных дифференциальных уравнений (4), решения нелинейной системы (1) можно записать в виде нелинейных интегральных уравнений второго рода. В частности, для несколько упрощенного варианта – при c1(Δy) = K1; c2(y2) ≠ K2, общее решение системы (1) будет определяться интегралами:
y1(t) = y01 (t) + W01(t)
где
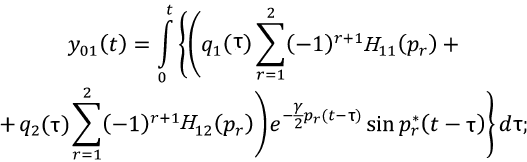 (19)
(19)
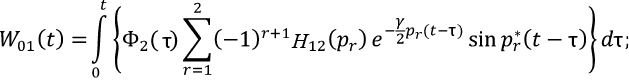 (20)
(20)
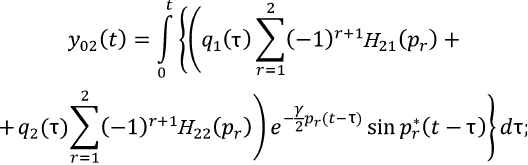 (21)
(21)
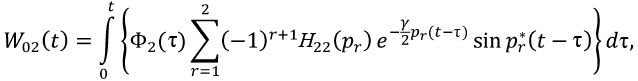 (22)
(22)
где y0i и W0i – соответственно решение линейной системы (4) и составляющие решений от «фиктивной» нагрузки. Φ2(τ) – по формуле (2).
При вычислении интегралов представляется оптимальным шаговый метод по времени с уточнением (итерацией) нелинейных зависимостей на каждом этапе. Если воспользоваться представлением подынтегральной функции
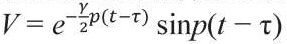
и соответственно ИПФ в виде сумм слагаемых, каждое из которых – произведения функций от t и τ, алгоритм расчета подобных систем можно записать в более компактном виде.
В частности, перемещения от фиктивной нагрузки в системе с одной степенью свободы
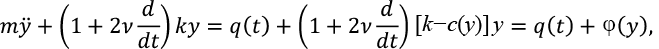 (23)
(23)
могут вычисляться по формулам [3]:
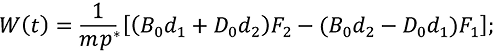 (24)
(24)
где
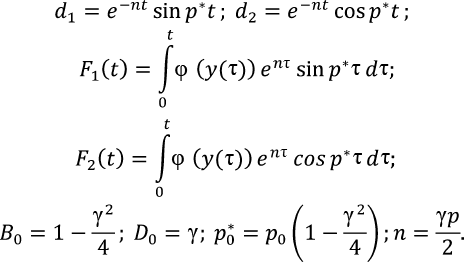 (25)
(25)
Алгоритмы построения решений (перемещений) системы нелинейных дифференциальных уравнений (1), записанных в виде сумм двух интегралов типа свертки (19)–(22), можно проиллюстрировать на примере уравнения (19). Воспользовавшись зависимостями (24), (25), составляющие решения по первой форме собственных колебаний системы линейных «порождающих» уравнений следует записать в виде
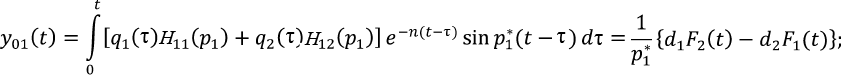 (г)
(г)
где
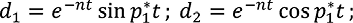 (д)
(д)
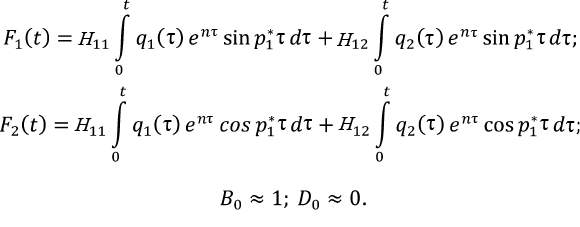 (е)
(е)
При вычислении перемещений по второй форме в (г) и (е) p1* следует заменить на p2* и поменять знак перед общим решением (г).
Точность построенных по формулам (24), (25) решений подобных систем оценивалась на примере уравнения (23) [8] при кубической зависимости «жесткость–перемещение» на нагрузки, возбуждаемые при работе виброактивного оборудования с вращающимися частями (насосы, вентиляторы и т. п.) при всех режимах – рабочем,
пуска
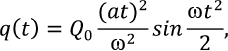
и остановки (26)
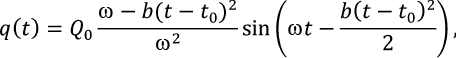
где постоянные a и b определяют время пуска и остановки.
В принятом алгоритме расчета при вычислении интегралов и, следовательно, полного решения системы (1) в качестве основного параметра, определяющего, главным образом, точность решений, был принят интервал по времени 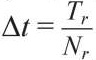 , где Tr – период колебаний, Nr – число разбиений. При
, где Tr – период колебаний, Nr – число разбиений. При 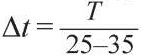 погрешность решений по отношению к решениям при Δt, существенно меньше принятого, не превышала одного процента.
погрешность решений по отношению к решениям при Δt, существенно меньше принятого, не превышала одного процента.
При достаточно малых значениях Δt возможно не уточнять величину нелинейной составляющей (не выполнять итерации), а при вычислении интегралов F1, F2 на каждом этапе принимать их средние значения.
Результаты
Подобный алгоритм был использован и при расчете системы с одной и двумя степенями свободы (рис. 2), дополнительная связь в которых включает демпфер вязкого трения [2]. Зависимости, построенные по результатам расчетов обеих систем, приведены на рис. 3–5.
В обоих случаях построенные решения учитывают все особенности, характерные для нелинейных систем, – срыв перемещений (при резонансе происходит переход с верхней возрастающей ветви на нижнюю – устойчивую) и связанное с этим возбуждение свободных колебаний.
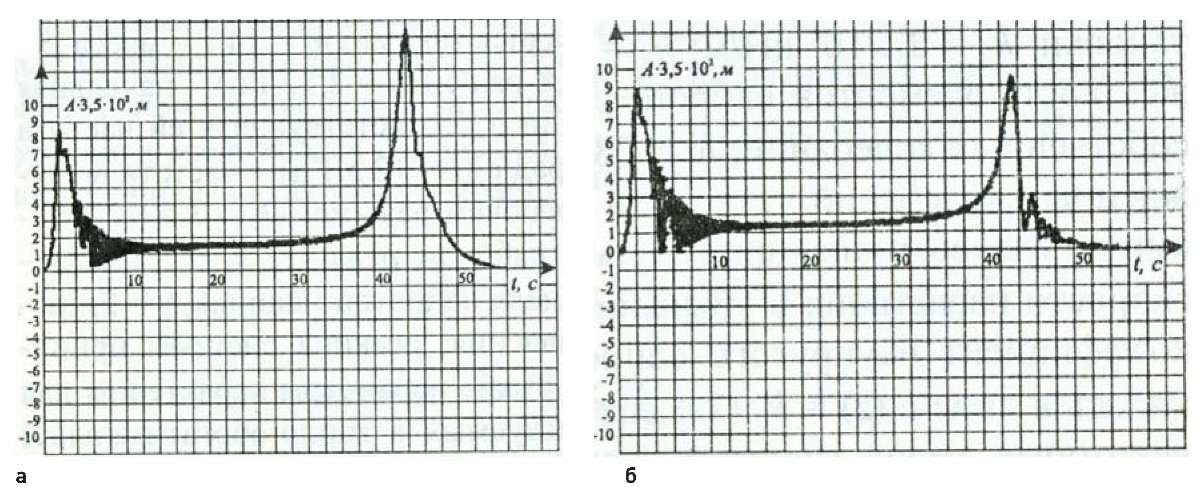
Рис. 3. Перемещения y = A × 103(м):
а – линейная система; б – система с кубической характеристикой
Fig. 3. Displacements y = A × 103(m):
a – linear system; б – cubic system
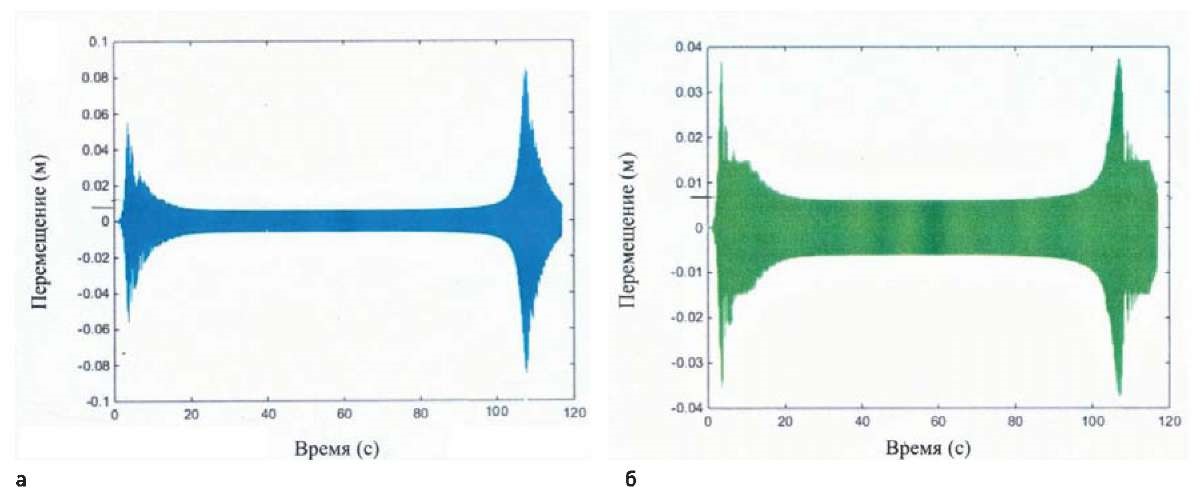
Рис. 4. Перемещения, (м), в системе с одной степенью свободы:
а – линейная система; б – с демпфером вязкого трения
Fig. 4. Displacements, (m), in a system with one degree of freedom:
a – linear system; b – with a viscous damper
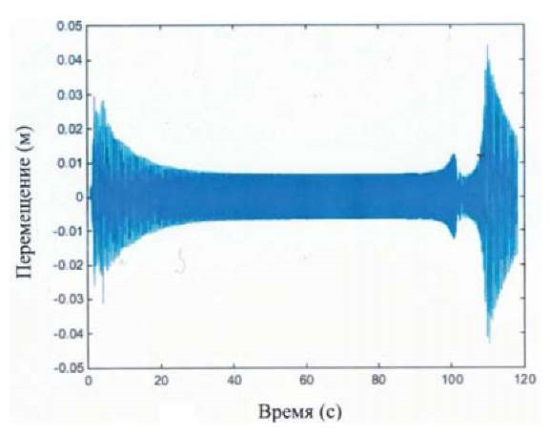
Рис. 5. Перемещения массы m2 в системе с двумя степенями свободы
Fig. 5. Mass displacements m2 in a system with two degrees of freedom
Выводы:
- применение методов, основанных на передаточных и переходных функциях при расчетах динамических систем в линейной постановке, позволяет построить достаточно компактные алгоритмы динамического расчета систем с конечным числом степеней свободы при произвольных, в частности периодических, воздействиях, в том числе в зонах резонанса;
- подобный подход позволяет существенно сократить этапы расчета по сравнению с традиционным методом «нормальных форм», а решения записать непосредственно относительно обобщенных, а не главных координат также в виде разложения по собственным формам;
- позволяет упростить запись разрешающих интегральных уравнений, в том числе для нелинейных систем;
- общий метод и алгоритмы расчета проиллюстрированы в работе на примере системы с двумя степенями свободы, которая вместе с тем является основной расчетной схемой для многих систем виброзащиты (виброизоляции) с динамическими гасителями колебаний, выключающимися связями и т. п. как в линейных, так и в нелинейных системах при произвольных силовых или кинематических воздействиях;
- разрешающими уравнениями при решении задач динамического расчета нелинейных систем с конечным числом степеней свободы являются нелинейные интегральные уравнения второго рода, к которым сводятся дифференциальные уравнения;
- основными зависимостями, определяющими алгоритм расчета, являются импульсные переходные функции линейных «порождающих» уравнений, представленные в виде разложения по формам собственных колебаний непосредственно относительно обобщенных координат;
- как следует из вида интегральных уравнений, решение исходной системы заключается, по существу, в вычислении двух интегралов типа свертки – от основной и «фиктивной» нагрузок;
- определяющим при вычислении интегралов шагами по времени является интервал Δt, при значениях которого
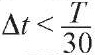 , построенные решения (также в виде разложения по формам собственных колебаний порождающей системы) могут определяться как «практически точные», т. е. с заданной заранее погрешностью;
, построенные решения (также в виде разложения по формам собственных колебаний порождающей системы) могут определяться как «практически точные», т. е. с заданной заранее погрешностью; - сходимость и точность построенных решений оценивалась на примерах расчета двух нелинейных систем: с одной степенью свободы при кубической зависимости «перемещение – реакция» и систем с одной и двумя степенями свободы (рис. 1) с выключающейся связью с демпфером вязкого трения;
- построенные решения содержат все особенности, характерные для нелинейных систем, – срыв (скачок) перемещений при прохождении через резонанс и, что существенно, связанное с этим возбуждение свободных колебаний;
- представляется, что подобный алгоритм расчета может достаточно эффективно применяться при исследовании нелинейных систем с различными расчетными схемами, в том числе со многими степенями свободы.
Список литературы
1. <i>Волкова М.В., Чернов Ю.Т., Кбейли Д.</i> Расчет массивых фундаментов, заглубленных в грунт, под виброизолированное и невиброизолированное оборудование. Известия высших учебных заведений. Строительство. 2020;(7):5–12.
2. <i>Солодовников В.В.</i> Статистическая динамика линейных систем автоматического управления. Москва: Физматгиз; 1960.
3. <i>Чернов Ю.Т.</i> Вибрации строительных конструкций. Аналитические методы расчета. Основы проектирования и нормирования вибраций строительных конструкций, подвергающихся эксплуатационным динамическим воздействиям. 2-е изд., испр. и доп. Москва: Изд-во АСВ, 2011.
4. <i>Чернов Ю.Т., Новожилов А.И.</i> Передаточные и импульсные переходные функции в задачах динамического расчета массивных фундаментов и систем виброизоляции. Сейсмостойкое строительство. Безопасность сооружений. 2006;(1):55–59.
5. <i>Розенвассер Е.Н.</i> Периодически нестационарные системы управления. Москва: Наука; 1973.
6. СП 26.13330.2012. Фундаменты машин с динамическими нагрузками. Актуализированная редакция СНиП 2.02.05-87. Москва: ФАУ «ФЦС»; 2012.
7. СП 413.1325800.2018. Здания и сооружения, подверженные динамическим воздействиям. Правила проектирования (с Изменением № 1). Москва: Стандартинформ; 2019.
8. <i>Чернов Ю.Т.</i> О выборе порождающих систем при исследовании нелинейных колебаний. Динамика строительных конструкций. Сб. научных трудов ЦНИИСК им. В.А. Кучеренко. Москва; 1985, с. 22–23.
9. <i>Боголюбов Н.Н., Митропольский Ю.А.</i> Асимптотические методы в теории нелинейных колебаний. 2-е изд. Москва: Физматгиз; 1981.
10. <i>Вульфсон И.И., Коловский М.З.</i> Нелинейные задачи динамики машин. Москва: Машиностроение; 1968.
11. <i>Ивович В.А., Онищенко В.Я.</i> Защита от вибрации в машиностроении. Москва: Машиностроение; 1990.
12. <i>Коловский М.З.</i> Нелинейная теория виброзащитных систем. Москва: Наука; 1966.
13. <i>Петров И.А., Осипова М.В.</i> О двух методах расчета нелинейных систем с одной степенью свободы. Интернет-вестник ВолгГАСУ. 2012;(3). Режим доступа: http://vestnik.vgasu.r u/attachments/PetrovOsipova-2012_3(23).pdf
14. <i>Чернов Ю.Т., Романенко А.Б.</i> К расчету нелинейных систем виброизоляции. Сейсмостойкое строительство. Безопасность сооружений. 2002;(4):34–38.
15. <i>Чернов Ю.Т., Зебилила М.</i> К расчету систем виброизоляции с демпферами вязкого трения. Сейсмостойкое строительство. Безопасность сооружений. 2018;(2):34–38.
16. <i>Diala U.H., Ezeh G.N.</i> Nonlinear demping for vibration isolation and control using semi active methods. SAVAP International. 2012;3(3):141–152.
17. <i>Khan W., Akhtar S., Hussain A.</i> Non-Linear time history analysis of tall structure for seismic load using damper. International Journal of Scientific and Research Publications. 2014;4(4):1–5.
Об авторе
Ю. Т. ЧерновРоссия
Юрий Тихонович Чернов, д-р техн. наук, профессор
e-mail: chernovyu.t.@yandex.ru
Рецензия
Для цитирования:
Чернов Ю.Т. Интегральные уравнения второго рода в задачах расчета нелинейных систем с конечным числом степеней свободы при произвольных динамических воздействиях и характере физических зависимостей. Вестник НИЦ «Строительство». 2023;38(3):155-167. https://doi.org/10.37538/2224-9494-2023-3(38)-155-167. EDN: YGYKIE
For citation:
Chernov Yu.T. Integral equations of the second kind in dynamic analysis of nonlinear systems with a finite number of degrees of freedom under arbitrary dynamic loading and material dependencies. Bulletin of Science and Research Center of Construction. 2023;38(3):155-167. (In Russ.) https://doi.org/10.37538/2224-9494-2023-3(38)-155-167. EDN: YGYKIE


























