Перейти к:
Свободные колебания балок переменного сечения при учете сил вращения и сил трения
https://doi.org/10.37538/2224-9494-2024-1(40)-7-20
EDN: ASUWBY
Аннотация
Введение. В настоящее время в строительстве широко используются балки в качестве несущих конструкций мостов, эстакад, покрытий, перекрытий, лестниц, площадок под оборудование и т. д. Для полного использования несущей способности конструкции и уменьшения расхода материала применяют балки переменного сечения по длине. При эксплуатации такие элементы конструкции подвергаются различным видам колебаний. Возникает необходимость рассмотрения вопросов колебательного движения.
Цель настоящей статьи состоит в применении численных методов при исследовании влияния инерционных сил вращения и при наличии сил вязкого трения на свободные колебания балок переменного сечения, которые приводят к определенным трудностям. Эта область исследования, несомненно, представляет большой интерес, так как расчеты прямо связаны с определением частот и форм собственных колебаний конструкций.
Материалы и методы. Свободные колебания описываются однородным дифференциальным уравнением в частных производных гиперболического типа. Используются методы разделения переменных, конечных разностей. Вводятся дискретная область в виде множества узлов равномерной сетки и однородная система алгебраических уравнений. Используется система уравнений в матрично-векторной форме.
Результаты. Определяются спектры собственных частот, коэффициенты затухания и собственные формы колебаний балки. Показано, что матрица коэффициентов является ленточной и пятидиагональной. Элементы матрицы являются функциями характеристического показателя. Коэффициент затухания и частота свободных колебаний определяются из системы двух нелинейных уравнений. Решение системы уравнений находится с помощью метода покоординатного спуска. Рассмотрен пример расчета балки из сварного двутавра. Вычислены пять элементов спектров коэффициентов затухания и собственных частот.
Выводы. Использование современных вычислительных комплексов MATLAB позволяет сочетать численные и графические способы. В решенных примерах удачно применены достоинства этих способов для определения собственных значений матриц и собственных функций, продемонстрирована надежность и высокая точность полученных результатов, позволяющая простым и универсальным способом определять характеристики свободных колебаний балок переменного сечения.
Ключевые слова
Для цитирования:
Барагунова Л.А., Шогенова М.М., Шогенов О.М., Яфаунов Э.А. Свободные колебания балок переменного сечения при учете сил вращения и сил трения. Вестник НИЦ «Строительство». 2024;40(1):7-20. https://doi.org/10.37538/2224-9494-2024-1(40)-7-20. EDN: ASUWBY
For citation:
Baragunova L.A., Shogenova M.M., Shogenov O.M., Yafaunov E.A. Free vibrations of variablesection beams taking rotational and frictional forces into account. Bulletin of Science and Research Center of Construction. 2024;40(1):7-20. (In Russ.) https://doi.org/10.37538/2224-9494-2024-1(40)-7-20. EDN: ASUWBY
Введение
Во многих случаях изучение колебаний балок существенно усложняется по разным причинам: материал балки неоднородный, поперечное сечение переменное вдоль оси, балка несет неравномерно распределенную массу и т. д. [1–3]. В таких задачах применение аналитических методов, например при определении собственных значений, амплитудно-частотных характеристик, встречает серьезные затруднения. Выход из них состоит в использовании численных методов, область применения которых все время расширяется и охватывает новые задачи [4–6].
Свободные колебания
Свободные колебания балки при наличии вязкого трения и с учетом инерции вращения описываются однородным дифференциальным уравнением в частных производных гиперболического типа [7–9], которое для балки переменного сечения из однородного материала примет вид1
(Bu″)″ – Pu″ – rü″ + mü + εmu̇ = 0,
(x, t) ∈ Q ≡ [ (x, t): x ∈ L ≡ (0, l), t > 0 ], (1)
где
B(x) = EJ(х), r(x) = ρJ(х), m(x) = ρF(х),
P – осевая растягивающая сила;
E, ρ – модуль упругости и плотность материала;
F, J – площадь и осевой момент инерции поперечного сечения балки;
ε – коэффициент удельного линейно-вязкого трения.
Точки соответствуют дифференцированию по времени t, штрихи – по пространственной координате x.
В уравнении (1) в порядке следования слагаемых учтены силы упругости, осевая сила, силы инерции вращения, инерционная сила линейных перемещений, силы линейно-вязкого трения [10–12].
Зададимся дальнейшей целью определить спектры собственных частот, коэффициентов затухания и собственных форм колебаний балки. Возьмем наиболее типичный случай шарнирно опертой однопролетной балки, для которой граничные условия представляются в виде
u(0,t) = u″(0,t) = u(1,t) = u″(1,t). (2)
Решение задачи (1), (2) отыскивается с помощью метода разделения переменных как произведение
u(x,t) = X(x)eλt. (3)
Здесь характеристический показатель
λ = – μ + jω, (4)
где j – мнимая единица;
μ и ω – подлежащие определению коэффициент затухания и частота свободных колебаний.
Подстановка (3) в (1), (2) дает
(BX″) – PX″ – rλ2X″ +(mλ2 + εmλ)X, (5)
X(0) = X″(0) = X(1) = X″(1) = 0. (6)
Введем обозначения
g(x) = P + rλ2, s(x) = mλ2 + εmλ
и перепишем уравнение (5)
(BX″)″ – gX″ + sX = 0. (7)
Далее воспользуемся методом конечных разностей. С этой целью вместо области L + Г
(Г – граничные точки) введем дискретную область lh в виде множества узлов равномерной сетки с шагом h
lh ≡ [ xi: xi = (i – 1)h, i = 1, 2, …, n, N; N = n + 1], h = l/n,
где N – количество узлов сетки.
Значения функций и производных в уравнении (7) заменим приближенными или точными (если возможно)
X(xi) ≈ yi,
X″(xi) ≈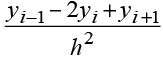 ,
,
g(xi) = gi, s(xi) = si
и получим на первом этапе равенство
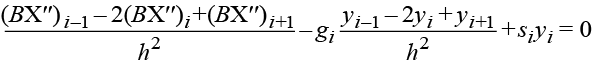 . (8)
. (8)
Повторное применение процедуры замены второй производной конечноразностными соотношениями и приведение подобных членов дает однородную систему алгебраических уравнений
ai yi–2 – bi yi–1 + ci yi – di yi+1+ ei yi+2 = 0, i = 4, 5, …, n – 2, (9)
где
ai = Bi–1, bi = 2Bi–1 + 2Bi + gih2,
ci = Bi–1 + 4Bi + Bi+1 + 2gih2 + sih4,
di = 2Bi + 2Bi+1 + gih2, ei = Bi+1.
Аналогичные замены проведем в граничных условиях (6), воспользуемся уравнением (9) для точек i = 2, 3, n – 1, n и получим четыре уравнения
q2 y2 – d2 y3 + e2 y4 = 0,
– b3 y2 + c3 y3 – d3 y4 + e3 y5 = 0,
an–1 yn–3 – bn–1 yn–2 + cn–1 yn–1 – dn–1 yn = 0,
an yn–2 – bn yn–1 + pn yn = 0.
Здесь обозначено
q2 = c2 – a2,
pn = cn – en.
Появляющиеся при этом значения функции во внесеточных узлах y0, yn+2 выражаются через значения функции в узлах сетки. Так, например, использование граничного условия на левом конце
X″(0) = 0
при i = 1 приводит к соотношению
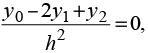
из которого при y1 = 0 легко получается, что
y0 = – y2.
Аналогично граничные условия на правом конце дают
yn+2 = – yn.
Исключим с помощью данных соотношений y0 и yn+2 из числа компонентов вектора y, а также равные нулю y1 и yN и получим вектор yT = {y2, y3, …, yn–1, yn}, компонентами которого являются отклонения балки. Тогда систему уравнений можно переписать в матрично-векторной форме
G(λ) y = 0, (10)
где G(λ) – квадратная матрица порядка n – 1. Можно легко показать, что матрица коэффициентов является ленточной и пятидиагональной вида
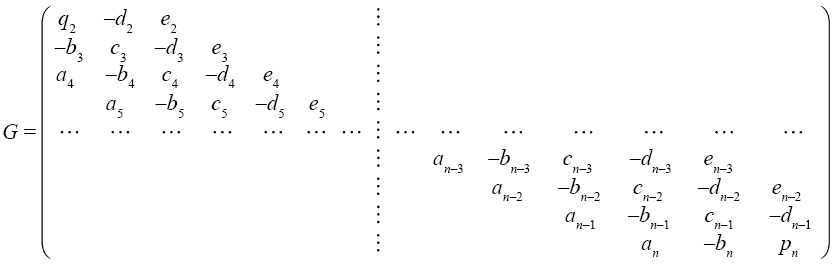
Здесь нулевые элементы не выписаны.
Элементы матрицы G являются функциями характеристического показателя λ и через него – коэффициента затухания μ и частоты колебаний ω в соответствии с (4).
Условие существования нетривиального решения системы уравнений (10) дает частотное уравнение
det G(λ) = 0, (11)
из которого определяются собственные значения, т. е. спектр {λ1, λ2, …}.
Левая часть уравнения (11) является полиномом порядка 2(n – 1), само же уравнение тогда оказывается алгебраическим вида f(λ) = 0. При больших значениях n его написание в развернутой форме, хотя и возможно, представляет громоздкую процедуру. Кроме того, получить его аналитические решения удается лишь в простейших случаях. Выход из таких затруднений состоит в применении численных методов и ЭВМ. При этом будем ориентироваться на алгоритмические языки и программные системы, позволяющие непосредственно пользоваться функциями комплексной переменной и проводить алгебраические и другие действия над ними (например, MathCad, C++, MATLAB [13–15] и т. д.).
Уравнение (11) с учетом того, что его левая часть представляет комплексную функцию, можно переписать в виде
f1(μ, ω) + j f2(μ, ω) = 0.
Отсюда следует, что коэффициент затухания μ и частота свободных колебаний ω должны определяться из системы двух нелинейных уравнений
f1(μ, ω) = 0, f2(μ, ω) = 0. (12)
Лишь при небольших значениях n, не представляющих интереса из-за недостаточной точности, решения задачи выписываются в явном виде. При больших значениях n можно обойтись без явного развертывания определителя матрицы G и получения формул для корней алгебраического уравнения (11). Рассмотрим подробнее.
Приравнивание к нулю действительной и мнимой частей определителя дает систему уравнений (12), корни которой могут быть найдены лишь численными методами. Использование современных вычислительных компьютерных программных систем типа MATLAB при этом позволяет весьма удачно сочетать достоинства как численных, так и графических способов.
Решение системы уравнений найдем с помощью метода покоординатного спуска [16–18]. С этой целью образуем вспомогательную неотрицательную функцию
Φ(μ, ω) = | det (μ, ω) | = [f 12(μ, ω) + f 22(μ, ω)]1/2,
обращающуюся в нуль лишь в том случае, если
f1(μ, ω) = f2(μ, ω) = 0.
Таким образом, решение исходной системы (12) будет одновременно точкой нулевого минимума скалярной функции векторного аргумента Ф(μ, ω), так что теперь необходимо решать более простую задачу
Ф(z) = 0, z = {μ, ω} ∈ R2 ∩ (μ > 0, ω > 0).
Здесь вектор z соответствует искомым величинам, Ф(z) представляет мультимодальную функцию, имеющую множество локальных минимумов.
Суть применяемого метода состоит в построении последовательности точек (приближений к решению) zk, k = 0, 1, ..., сходящейся к точке локального минимума z*. При этом в процессе вычислений необходимо добиваться, чтобы значения вспомогательной функции были монотонно убывающими и ограниченными снизу
Ф(z0) ≥ Ф(z1) ≥.... ≥ Ф(zk) ≥.... ≥ Ф(z*). (13)
Для реализации такой цели вначале с помощью численных экспериментов намечается начальная точка последовательности z0. Затем определяются последующие приближения zk с помощью соотношений
zk+1 = zk + Δk,
где Δk – вектор приращений координат, обеспечивающий выполнение условий (13).
Условием прекращения вычислительной процедуры, а значит, и признаком достижения корня с необходимой точностью служит выполнение неравенства
Ф(zk+1) < δ, (14)
причем δ – априорно задаваемое малое положительное число (точность вычислений).
Многократное повторение такой процедуры вычислений дает спектры коэффициентов затухания и собственных частот
{(μ1, ω1), (μ2, ω2),…}.
При реализации предлагаемой численной схемы наибольшая сложность состоит в правильном выборе приращений координат Δ = {Δμ, Δω} на каждом шаге по величине и по знаку. В этом месте обычные подходы к составлению компьютерных программ вычислений требуют высокого программистского искусства, а сами программы получаются сложными и громоздкими. Трудности существенно упрощаются, если используемая система программирования позволяет оперативно визуализировать результаты вычислений. Поясним сказанное на примере данной задачи при пользовании программной системой MATLAB. Один из аргументов функции Φ(μ, ω), например μ, фиксируется, вычисляются ординаты функции Φ(ω | μ), на экран компьютера выводится ее график (рис. 1а), вычисления приостанавливаются. По кривой, являющейся сечением поверхности Φ(μ, ω), отчетливо видны условные минимумы функции Φ(ω | μ). Теперь фиксируем аргумент ω на значении, соответствующем условному минимуму и строим новый график Φ(μ | ω) (рис. 1б) и т. д. Такая процедура продолжается до выполнения условия (14).
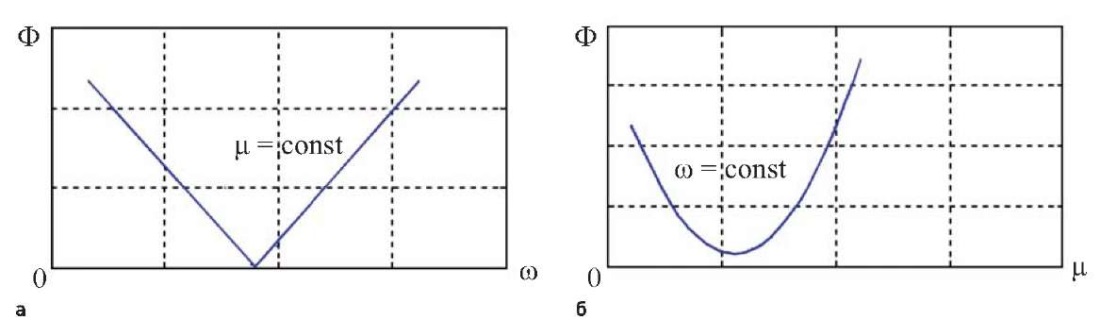
Рис. 1. Графики, полученные программной системой MATLAB
Fig. 1. Graphs obtained by the MATLAB toolbox
Пример 1. В качестве тестовой проверки рассмотрим балку постоянного сечения из двутавра № 14 с численными данными
l = 4 м, n = 400, ρ = 7800 кг/м3, E = 200 ГПа,
F = 17,4 см2, J = 572 см4, ε = 0,01 с-1, P = 0.
По процедуре, описанной выше, определены пять элементов спектра собственных частот. Их значения представлены в табл. 1.
Таблица 1
Элементы спектра собственных частот
Таble 1
Elements of the spectrum of eigenfrequencies
|
k |
1 |
2 |
3 |
7 |
10 |
|
μk, с-1 |
0,00499 |
0,00496 |
0,00491 |
0,00455 |
0,00416 |
|
ωk, с-1 |
178,91 |
713,46 |
1597,23 |
8367,43 |
16321,99 |
В табл. 2 показаны значения пяти элементов спектра собственных частот для балки с такими же численными данными при Р = –0,25Рэ (Рэ – критическая эйлерова сила).
Таблица 2
Элементы спектра собственных частот при Р = –0,25Рэ
Таble 2
Elements of the spectrum of eigenfrequencies at Р = –0.25Рэ
|
k |
1 |
2 |
3 |
7 |
10 |
|
μk, с-1 |
0,00499 |
0,00496 |
0,00491 |
0,00455 |
0,00416 |
|
ωk, с-1 |
154,94 |
690,80 |
1574,88 |
8346,05 |
16301,57 |
Примечательно, что для получения результатов требуется небольшое количество шагов в методе покоординатного спуска (4–5 для каждого k).
Тот же спектр (при Р = 0), полученный точными аналитическими методами, приведен в табл. 3.
Таблица 3
Элементы спектра собственных частот при Р = 0
Таble 3
Elements of the spectrum of eigenfrequencies at Р = 0
|
k |
1 |
2 |
3 |
7 |
10 |
|
μk, с-1 |
0,00499 |
0,00496 |
0,00491 |
0,00455 |
0,00416 |
|
ωk, с-1 |
178,91 |
713,47 |
1597,3 |
8369,44 |
16329,7 |
Ниже в табл. 4 показана разница между собственными частотами колебаний балки, полученными точными аналитическими методами и методом конечных разностей.
Таблица 4
Разница между собственными частотами колебаний балки
Таble 4
Difference between eigenfrequencies of beam vibrations
|
k |
1 |
2 |
3 |
7 |
10 |
|
Разница, % |
0 |
0,001 |
0,004 |
0,024 |
0,047 |
Видно, что разница небольшая, не имеющая практической значимости.
Результаты данного примера убедительно показывают, что метод конечных разностей дает надежные результаты, позволяющие универсальным и простым способом определять динамические характеристики свободных колебаний балок переменного сечения [19–20].
Спектр собственных форм может быть установлен с помощью системы уравнений (10). Ввиду того, что определитель матрицы G равен нулю, собственные формы могут быть найдены лишь с точностью до сомножителя. Тогда в (10) можно принять, например, что y2 = 1, и остальные неизвестные найти из системы уравнений, из которой исключена последняя строка (см. на стр. 16).
Заметим, что правая часть системы уравнений образована из элементов первого столбца матрицы G.
Пример 2. По данным примера 1 вычислим ординаты трех первых собственных форм φk(х) = yk(x).
Результаты счета в виде графиков показаны на рис. 2. Номера кривых при этом совпадают с номерами собственных частот; проведена нормировка форм, удовлетворяющая условию
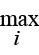 | yi | = 1.
| yi | = 1.
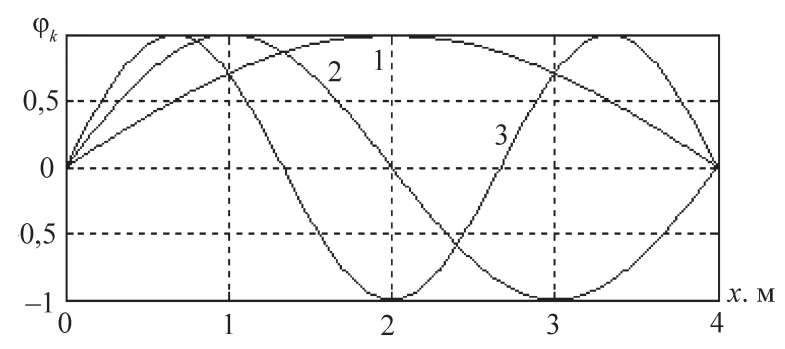
Рис. 2. Ординаты первых собственных форм φk(х) = yk(x)
Fig. 2. Ordinates of the first eigenforms φk(x) = yk(x)
Данные кривые почти неразличимо совпадают с собственными формами, найденными с помощью точных аналитических методов.
Пример 3. Рассмотрена балка из сварного двутавра длиной 4 м, состоящая из трех участков, поперечное сечение которых изменяется по длине (рис. 3), с численными данными
ρ = 7800 кг/м3, E = 200 ГПа, n = 500, ε = 0,01 c-1, l1 = l3 = 1 м, F1 = F3 = 61,9 см2,
J1 = J3 = 13 380 см4, l2 = 2 м, F2 = 84,7 см2, J2 = 27 696 см4.

Рис. 3. Схема балки
Fig. 3. Beam diagram
По процедуре, описанной выше, определены пять элементов спектров коэффициентов затухания и собственных частот. Их значения представлены в табл. 5.
Таблица 5
Элементы спектров коэффициентов затухания и собственных частот
Table 5
Elements of spectra of damping coefficients and eigenfrequencies
|
k |
1 |
2 |
3 |
4 |
5 |
|
μk, с-1 |
0,00494 |
0,00474 |
0,00440 |
0,00396 |
0,00354 |
|
ωk, с-1 |
526,02 |
1913,70 |
4209,43 |
7332,23 |
10761,67 |
В табл. 6 представлены те же пять элементов спектров коэффициентов затухания и собственных частот для классической модели.
Таблица 6
Элементы спектров коэффициентов затухания и собственных частот
для классической модели
Table 6
Elements of spectra of damping coefficients and eigenfrequencies
for a classical model
|
k |
1 |
2 |
3 |
4 |
5 |
|
μk, с-1 |
0,005 |
0,005 |
0,005 |
0,005 |
0,005 |
|
ωk, с-1 |
530,69 |
1971,84 |
4494,04 |
8247,98 |
12782,02 |
В табл. 7 показана разница между собственными частотами балки по двум моделям.
Таблица 7
Разница между собственными частотами балки по двум моделям
Table 7
Difference between eigenfrequencies of the beam according to two models
|
k |
1 |
2 |
3 |
7 |
10 |
|
Разница, % |
0,88 |
2,95 |
6,33 |
11,10 |
15,81 |
Как и следовало ожидать, собственные частоты балки, модель которой учитывает инерционные силы вращения, меньше элементов спектра классической балки. Без учета вращения элементов балки делают систему жестче реальной балки, что приводит к завышенным частотам свободных колебаний. Разница становится существенной для колебаний по обертонам.
Заключение
- Метод конечных разностей дает надежные результаты, позволяющие универсальным и простым способом определять динамические характеристики свободных колебаний балок переменного сечения.
- Задача о колебаниях балки переменного сечения, представленная в статье, решена эффективно с помощью численного метода конечных разностей.
- Основное обыкновенное дифференциальное уравнение колебаний балки и уравнения граничных условий решаются легко, с помощью численного метода конечных разностей.
- Решение основных аналитических уравнений приводит к однородной алгебраической системе уравнений в матрично-векторной форме, что существенно облегчает достижение конечных целей.
1. В данной модели колебаний деформации сдвига не учитываются.
Список литературы
1. Ильин В.П., Карпов В.В., Масленников А.М. Численные методы решения задач строительной механики. Москва: Изд-во АСВ, СПб.: СПбГАСУ; 2005.
2. Караманский Т.Д. Численные методы строительной механики. Москва: Стройиздат; 1981.
3. Самарский А.А., Гулин А.В. Численные методы. Москва: Наука; 1989.
4. Формалев В.Ф., Ревизников Д.Л. Численные методы. Изд. 2-е. Москва: Физматлит; 2006.
5. Бидерман В.Л. Прикладная теория механических колебаний. Москва: Высшая школа; 1979.
6. Масленников А.М. Динамика и устойчивость сооружений. Москва: Юрайт; 2016.
7. Kulterbayev Kh.P., Shogenova M.M., Baragunova L.A. On the Influence of the Characteristic Frequency and Broadband of Seismic Effects on the Vertical Rod Oscillations. IOP Conference Series: Materials Science and Engineering. 2020;753(4):042040. https://doi.org/10.1088/1757-899x/753/4/042040
8. Барагунов Т.М. Об устойчивости многопролетных стержней на гибких опорах. В: Восьмые Окуневские чтения: материалы докладов международной конференции, 25–28 июня 2013 г., г. Санкт-Петербург, Россия. СПб.: Балтийский гос. технический ун-т; 2013, с. 72–74.
9. Культербаев Х.П., Барагунова Л.А. О реализации проблемы собственных значений сжато-растянутого стержня на компьютере. В: Компьютерные технологии в строительстве: материалы Всероссийской научно-технической конференции. Махачкала: Алеф (ИП Овчинников); 2013, с. 90–94.
10. Культербаев Х.П., Барагунова Л.А. О плотности собственных значений в задаче об устойчивости многопролетного стержня. В: Строительство: Проблемы и перспективы. Сборник статей по материалам международной научно-практической конференции. Махачкала: Дагестанский государственный институт народного хозяйства; 2013, с. 133–135.
11. Культербаев Х.П., Чеченов Т.Ю., Барагунов Т.М. Вынужденные колебания континуально-дискретной многопролетной балки при учете инерционных сил вращения. Вестник ВолгГАСУ. Серия: Строительство и архитектура. 2012;26:48–55.
12. Чеченов Т.Ю. Кинематически возбуждаемые колебания модифицированной балки Тимошенко. В: Надежность и долговечность строительных материалов, конструкций и оснований фундаментов. Материалы IV Международной научно-технической конференции (12–14 мая 2005 г.). Ч. II. Волгоград; 2005, с. 36–41.
13. Kulterb ayev Kh.P., Baragunova L.A., Lafisheva M.M. Determining Frequencies of Free Longitudinal Vibrations of Rods by Analitical and Numerical Metods. In: Alikhanov A., Lyakhov P., Samoylenko I. Current Problems in Applied Mathematics and Computer Science and Systems. APAMCS 2022. Lecture Notes in Networks and Systems, vol. 702. Springer Nature Switzerland; 2023, pp. 131–136. https://doi.org/10.1007/978-3-031-34127-4_13
14. Культербаев Х.П., Барагунова Л.А. Определение собственных значений и собственных функций в задаче о колебаниях балки переменного сечения. В: Строительство и архитектура: теория и практика сейсмической безопасности. Сборник научных статей по итогам деятельности международной научно-практической конференции, посвященной памяти д.т.н., профессора Абакарова А.Д. (14–16 марта 2023 г., г. Махачкала). Махачкала; 2023, с. 131–142.
15. Культербаев Х.П., Лафишева М.М., Цеева Ф.М. Вынужденные гармонические и случайные продольные колебания вертикального стержня. В: Строительство и архитектура: теория и практика сейсмической безопасности. Сборник научных статей по итогам деятельности международной научно-практической конференции, посвященной памяти д.т.н., профессора Абакарова А.Д. (14–16 марта 2023 г., г. Махачкала). Махачкала; 2023, с. 170–177.
16. Казиев А.М., Казиев И.А. Колебания балки с сосредоточенными массами на упругих опорах. В: Наука, техника и технология XXI века (НТТ-2013). Материалы V Международной научно-технической конференции (Нальчик, 2013 г.). Нальчик: Кабардино-Балкарский государственный университет; 2013.
17. Казиев А.М. Свободные колебания растянутой балки с сосредоточенными массами. В: Перспектива-2004. Материалы Всероссийская научная конференция студентов, аспирантов и молодых ученых. Т. III. Нальчик; 2004. с. 251–255.
18. Культербаев Х.П., Джанкулаев А.Я. Введение в MATLAB. Нальчик: КБГУ; 2006.
19. Барагунова Л.А., Кертбиев А.А. Расчет балок методом конечных разностей. В: Фундаментальные и прикладные научные исследования: актуальные вопросы современной науки, достижения и инновации. Сборник научных статей по материалам IX Международной научно-практической конференции (8 ноября 2022 г., г. Уфа). Уфа: Изд. НИЦ Вестник науки; 2022, с. 378–385.
20. Kulterbaev Kh. P., Vodakhova L.A., Baragunova L.A., Shogenova M.M., Tsipinova A.Kh. Free oscillations of a beam with installation (1st part). IOP Conference Series: Materials Science and Engineering. 2021;1083(1):012043. https://doi.org/10.1088/1757-899x/1083/1/012043
Об авторах
Л. А. БарагуноваРоссия
Лялюся Адальбиевна Барагунова, старший преподаватель кафедры строительных конструкций и механики
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
тел.: +7 (928) 075-62-99
М. М. Шогенова
Россия
Марьяна Мухарбиевна Шогенова, канд. ф.-м. наук, доцент, доцент кафедры строительных конструкций и механики
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
тел.: +7 (928) 710-50-45
О. М. Шогенов
Россия
Олег Мухамедович Шогенов, канд. техн. наук, доцент, доцент кафедры строительных конструкций и механики
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
тел.: +7 (928) 705-59-16
Э. А. Яфаунов
Россия
Эльдар Асланович Яфаунов, студент направления подготовки «Строительство»
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
тел.: +7 (938) 078-06-20
Рецензия
Для цитирования:
Барагунова Л.А., Шогенова М.М., Шогенов О.М., Яфаунов Э.А. Свободные колебания балок переменного сечения при учете сил вращения и сил трения. Вестник НИЦ «Строительство». 2024;40(1):7-20. https://doi.org/10.37538/2224-9494-2024-1(40)-7-20. EDN: ASUWBY
For citation:
Baragunova L.A., Shogenova M.M., Shogenov O.M., Yafaunov E.A. Free vibrations of variablesection beams taking rotational and frictional forces into account. Bulletin of Science and Research Center of Construction. 2024;40(1):7-20. (In Russ.) https://doi.org/10.37538/2224-9494-2024-1(40)-7-20. EDN: ASUWBY


























