Перейти к:
Численное моделирование динамической задачи обобщенной системы с распределенными параметрами
https://doi.org/10.37538/2224-9494-2024-1(40)-35-48
EDN: CYHKDR
Аннотация
Введение. В статье излагаются вопросы математического моделирования динамической задачи в виде обобщенной системы с одной степенью свободы. Қ таким системам относятся высотные сооружения башенного типа. Обеспечение сейсмостойкости уникальных объектов башенного типа является актуальной проблемой.
Целью работы является определения напряженно-деформированного состояния исследуемого объекта от внешнего воздействия в виде заданной акселерограммы землетрясения.
Материалы и методы. Использованы методы строительной механики, динамики сооружений, а также методы численного моделирования. На основе уравнения Лагранжа получено уравнение движения обобщенной системы с распределенными параметрами. Методика исследований включала построение математических моделей рассматриваемых систем, их численный анализ, сопоставление полученных результатов с имеющимися данными.
Результаты. Разработана математическая модель, позволяющая проводить исследования напряженно-деформированного состояния сооружения при различных внешних воздействиях, в том числе сейсмических. Дифференциальное уравнение обобщенной системы решается непосредственно с использованием метода последовательных аппроксимаций и с использованием интеграла Дюамеля на каждом шаге по времени. На основе разработанного алгоритма составлена компьютерная программа на языке FORTRAN и получены кинематические и статические данные исследуемого объекта. На примере сооружения башенного типа исследованы свободные колебания от действия мгновенного импульса и получены результаты от заданной акселерограммы землетрясения.
Выводы. Из полученных результатов следует, что период свободных колебаний объекта совпадает с результатами численного моделирования. Результаты, полученные численным дифференцированием, практически совпадают с результатами численного интегрирования при различных воздействиях. Достоверность результатов подтверждается сравнением результатов, полученных двумя методами. Разработанные компьютерные программы могут быть использованы для проведения мониторинга уникальных объектов башенного типа.
Ключевые слова
Для цитирования:
Низомов Д.Н., Сангинов А.М., Саломзода М.М. Численное моделирование динамической задачи обобщенной системы с распределенными параметрами. Вестник НИЦ «Строительство». 2024;40(1):35-48. https://doi.org/10.37538/2224-9494-2024-1(40)-35-48. EDN: CYHKDR
For citation:
Nizomov D.N., Sanginov A.M., Salomzoda M.M. Numerical simulation of the dynamic problem of a generalized system with distributed parameters. Bulletin of Science and Research Center of Construction. 2024;40(1):35-48. (In Russ.) https://doi.org/10.37538/2224-9494-2024-1(40)-35-48. EDN: CYHKDR
Рассмотрим динамическую модель сооружения, которая представляет собой систему с распределенной массой m(x) и сосредоточенными массами mj, установленными в некоторых точках (рис. 1). Данное сооружение башенного типа, в котором основными характеристиками являются изгибная жесткость EI(x) и погонная масса m(x), представляет систему с бесконечным числом степеней свободы. Если предположить, что перемещения сооружения ограничены только одной формой колебаний, то такая модель с обобщенной координатой w(t) может быть использована для расчета на сейсмические воздействия в виде заданной акселерограммы землетрясения. Таким образом, предполагается, что движение сооружения, как обобщенная система с одной степенью свободы, происходит только по одной форме в виде безразмерной функции φ(x) с амплитудой колебаний w(t). Следовательно, при такой форме движения перемещение и соответствующие производные по времени выражаются так:
 (1)
(1)
При заданном перемещении основания в виде функции w0(t), общие перемещение, скорость и квадрат скорости записываются таким образом:
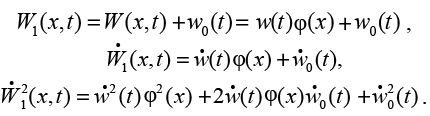 (2)
(2)
Для определения потенциальной энергии исследуемого объекта, который испытывает изгиб и продольное сжатие, необходимо иметь вторую производную от функции W(x,t) по x:
W″(x,t) = w(t) × φ″(x),
а также вертикальную составляющую верхней точки сооружения (рис. 1):
Δ = ∫l0 dΔ.
С учетом малости перемещения dΔ [1] можно написать:
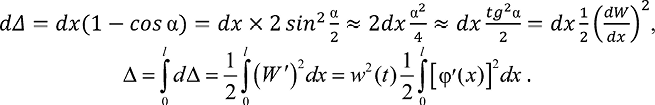 (2а)
(2а)
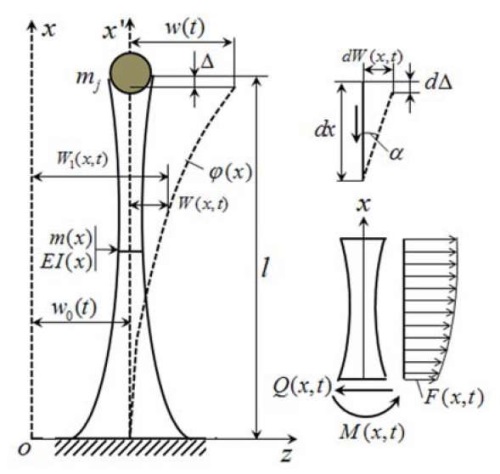
Рис. 1. Обобщенная система с распределенной массой
Fig. 1. Generalized system with distributed mass
Уравнение движения. Для вывода уравнений движения обобщенной системы воспользуемся уравнением Лагранжа второго рода, соответствующего вариационному принципу Гамильтона [2–4]:
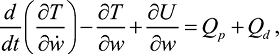 (3)
(3)
где T – кинетическая энергия;
U – потенциальная энергия деформации изгиба;
Qp – обобщенная сила (сила трения или внешняя возмущающая сила, зависящая от времени);
Qd – обобщенная сила сопротивления.
Кинетическая и потенциальная энергии модели, представленной на рис. 1, с учетом (1), (2) и (2а) записываются в виде:
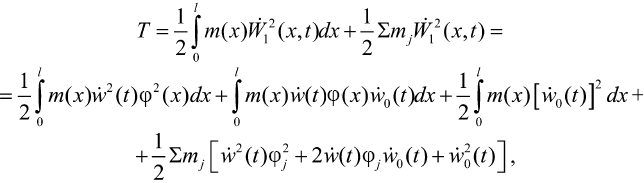
 (4)
(4)
где N(x) – нормальная сила от собственного веса сооружения, которая может изменяться по линейному закону.
Суммарная потенциальная энергия от изгибающего момента и сжимающей силы будет равняться
 (5)
(5)
Здесь предполагается, что опорная часть сооружения во время землетрясения приобретает только горизонтальное перемещение.
Производные от кинетической и потенциальной энергии с учетом (4) и (5) приобретают вид
 (6)
(6)
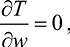 (7)
(7)
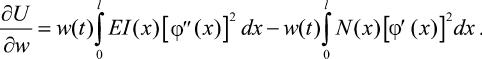 (8)
(8)
Обобщенная сила сопротивления определяется по формуле
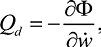
где Ф – диссипативная функция Рэлея [5][6], которая для системы с распределенными параметрами затухания представляется в виде
 (9)
(9)
Внося (6)–(9) в (3), получаем уравнение
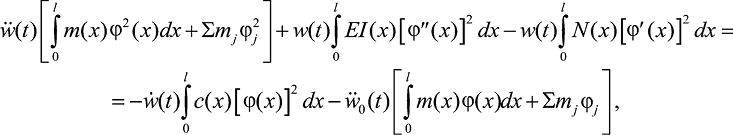
которое представляется в виде
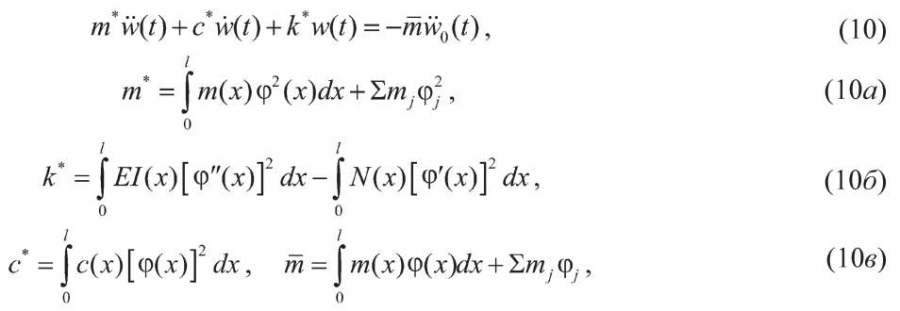
где m*, k*, c* – обобщенные масса, жесткость и затухания;
m – коэффициент сейсмического возмущения, который характеризует уровень возможных колебаний сооружения по форме φ(x) [7].
Поделив обе части (10) на обобщенную массу m*, получим
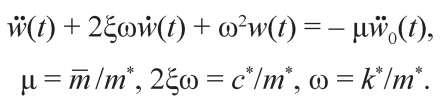 (11)
(11)
Дифференциальное уравнение (11) описывает динамическое состояние обобщенной системы с одной степенью свободы от сейсмического воздействия в виде заданной акселерограммы. Здесь предполагается, что функции φ(x), c(x), m(x), EI(x), N(x) будут заданы в зависимости от геометрических и физико-механических свойств исследуемого объекта. Коэффициент μ в (10) характеризует различие между одномассовыми системами с сосредоточенной и обобщенной массами.
Обобщенные характеристики. Рассмотрим сооружение башенного типа переменного сечения по высоте. Предполагается, что сооружение круглого сечения в плане состоит из двух центральных колец постоянного сечения, идущих от основания до верхней части объекта и наружных колец, число которых в зависимости от высоты уменьшается. При этом безразмерная функция формы φ(x), распределенная масса m(x), момент инерции I(x) и нормальная сила N(x) в исследуемом объекте изменяются по следующим законам:
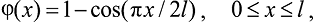 (12)
(12)
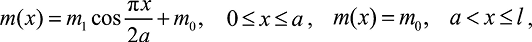 (13)
(13)
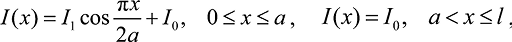 (14)
(14)
где m1, I1 – масса и момент инерции опорной части без учета центральной части;
m0, I0 – масса и момент инерции центральной части сооружения;
a – длина нижней части сооружения с переменным сечением.
Тогда из (10а) с учетом (12), (13) получим интегральное выражение обобщенной массы:
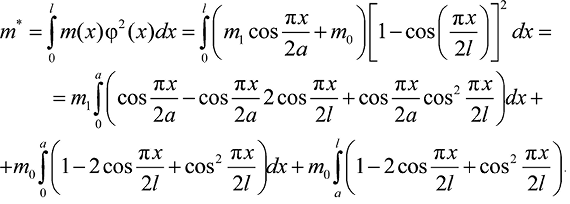 (15)
(15)
Из (10б) с учетом (14) и производных от функции формы
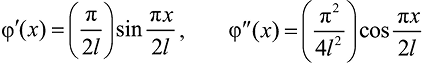
получим интегральное выражение обобщенной жесткости изгибающего момента
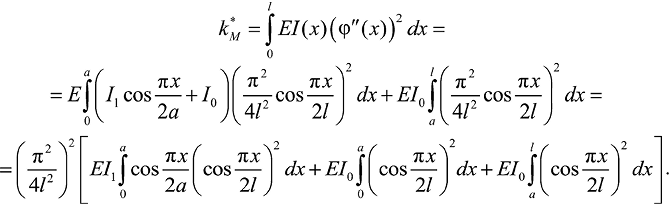 (16)
(16)
Если предположить, что нормальная сжимающая сила
N(x) = N = γ Aсрl, Aср(A1 + A0)/2,
где γ, A1, A0 – объемный вес, площади сечений элементов на внешних кольцах и в центральной части объекта, получаем
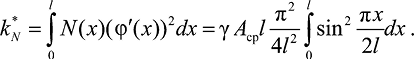 (17)
(17)
Обобщенная масса в правой части (10) выражается следующим образом
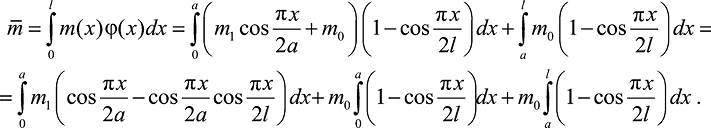 (18)
(18)
Если принять, что a = l/3, то непосредственным интегрированием [8] из (15)– (18) получим
m* = 0,06406 × m1l + 0,2268 × m0l,
k*M = π3(0,4167EI1 + 0,7854EI0)/8l3,
m = 0,005475m1l + 0,3634m0l,
k*N = 0,6168 (А1 + А0)γ,
2ξω = c*/m*, ξ = c*/m*2ω) = 0,05 (19)
Полученные обобщенные параметры системы (19), при заданных значениях m0, m1, I0, I1, A0, A1, позволяют перейти к решению дифференциального уравнения (11). Из решения уравнения (11) определяется w(t), а затем с использованием (1) вычисляются перемещения, скорость и ускорения в произвольных точках по оси x, соответствующие моменту времени t. Далее вычисляются внутренние усилия в сечениях исследуемого объекта.
При заданной правой части (11) в виде реальной или синтезированной акселерограммы решение осуществляется либо интегралом Дюамеля с последующим численным интегрированием, либо непосредственным численным дифференцированием. Ниже рассматривается реализация обоих методов на примере системы с распределенными параметрами.
Численное дифференцирование. С целью численного решения дифференциального уравнения (11) применим метод последовательных аппроксимаций [9][10], где скорость и ускорения, соответствующие моменту времени tn, представляются в виде
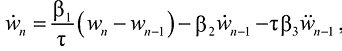 (20)
(20)
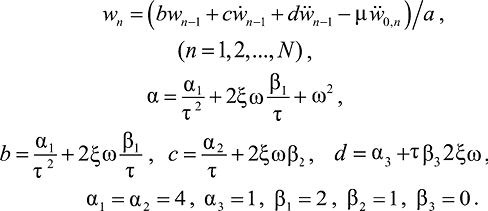 (21)
(21)
где αi, βi – числовые коэффициенты [11];
τ = tn – tn–1 – шаг по времени.
Записав уравнение (11) в момент времени tn и внося (20) и (21) в (11), после некоторых преобразований получим рекуррентную формулу для определения wn
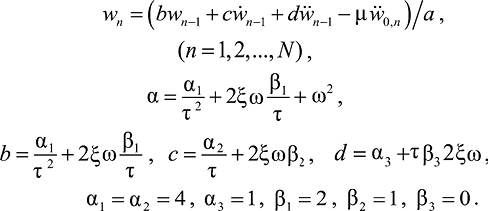 (22)
(22)
Затем с использованием (1) определяются перемещения, скорость и ускорения в произвольной точке координатной оси x, по длине сооружения, соответствующие моменту времени tn дискретной оси t
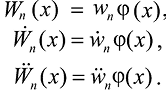 (23)
(23)
Затем вычисляются значения сил инерции и сил упругости:
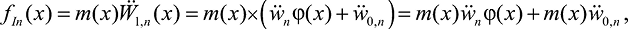 (24)
(24)
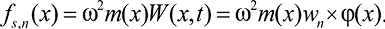 (25)
(25)
Поперечная сила и изгибающий момент в точке, расположенной на высоте h от основания сооружения, выражаются следующим образом:
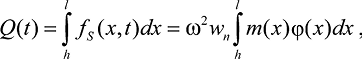 (26)
(26)
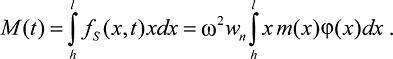 (27)
(27)
Если функции m(x) и φ(x) заданы, то интегралы (26) и (27) вычисляются непосредственным интегрированием.
Численное моделирование с применением интеграла Дюамеля. Решение уравнения (11) можно также представить интегралом Дюамеля [7]:
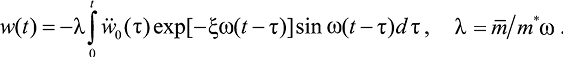 (28)
(28)
Этот интеграл с учетом
sinω(t – τ) sinωt cosωt – cosωτ sinωτ
представляется в виде
w(t) = – λ[a(ω)sinωt – b(ω)cosωt],
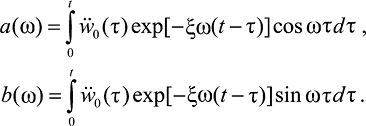 (29)
(29)
Интегралы a(ω) и b(ω) в (28) вычисляются методом Симпсона [12]. При этом шаг интегрирования выбирается в зависимости от шага оцифровки заданной акселерограммы ẅ0(t). Затем вычисляются перемещения, скорость и ускорения в произвольной точке сооружения:
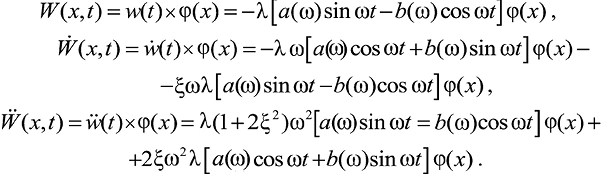 (30)
(30)
Далее определяются распределенная сила упругости, сдвигающая сила и изгибающий момент в основании сооружения:
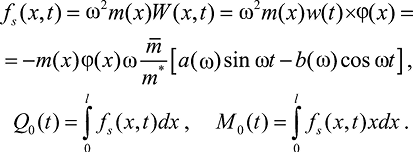
На основе изложенных выше алгоритмов численного моделирования были разработаны компьютерные программы и получены результаты от заданного воздействия в виде акселерограммы землетрясения.
Пример. В качестве примера рассматривается сооружение башенного типа (рис. 2), которое состоит из ряда колонн, расположенных во внешних кольцах, а также из двух центральных колец сплошного сечения, соединенных между собой диафрагмами жесткости (рис. 2б). При этом количество внешних колец постепенно уменьшается и на высоте x ≥ h1 остаются только центральные кольца.
Суммарные площади сечений, распределенные массы и моменты инерции несущих элементов центральных (A0, m0, I0) и пяти внешних колец (A1, m1, I1) равняются:
А0 = 27,09 м2, m0 = А0γ/g = 5,522 тс2/м2,
А1 = 47,38 м2, m1 = А1γ/g = 9,659 тс2/м2,
I0 = 229,4 м4, I1 = 9692,8 м4.(а)
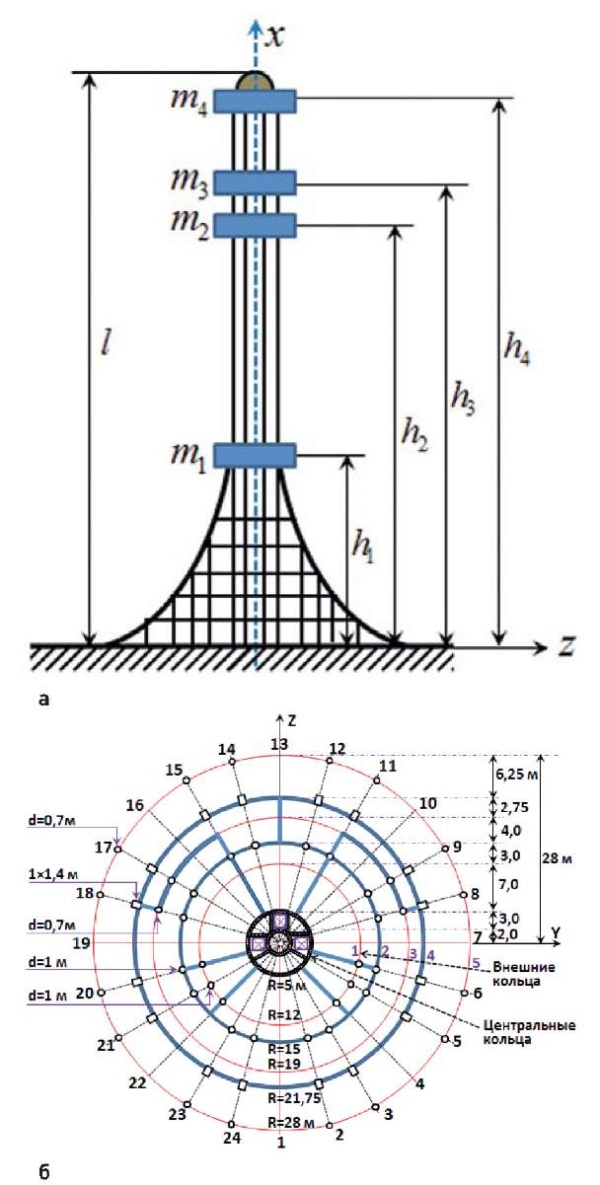
Рис. 2. Геометрия исследуемого сооружения
Fig. 2. Geometry of the investigated structure
Обобщенные массы, входящие в левую и правую части дифференциального уравнения (10) при высоте сооружения l = 120 м, получаются соответственно равными:
m* = 0,06406 × m1l + 0,2268 × m0l = 224,5 тс2/м,
m = 0,005475 m1l + 0,3634 m0l = 247,2 тс2/м, (б)
μ = m/m* = 1,101.
Обобщенные коэффициенты жесткости, соответствующие изгибу и сжатию сооружения при l = 120 м, Е = 2 × 106 т/м, γ = 2 т/м3, получаются равными:
k*M = π3(0,4167EI1 + 0,7854EI0) = 18926,8 т/м,
k*N = 0,6168(A0 + А1)γ = 91,85 т/м,(в)
k* = k*M – k*N = 18834,95 т/м.
Следовательно, частота и период свободных колебаний сооружения
ω = 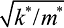 = 9,18 рад/с,
= 9,18 рад/с,
T = 2π/ω = 0,68 с.(г)
На основе разработанной программы на языке FORTRAN получены результаты как методом численного дифференцирования, так и методом численного интегрирования. Вначале, на основе (20)–(23), были исследованы свободные колебания сооружения. На рис. 3 показаны графики изменения перемещения wA и wL, полученные от действия мгновенного импульса при τ = 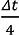 = 0,005 с и ξ = 0,05.
= 0,005 с и ξ = 0,05.
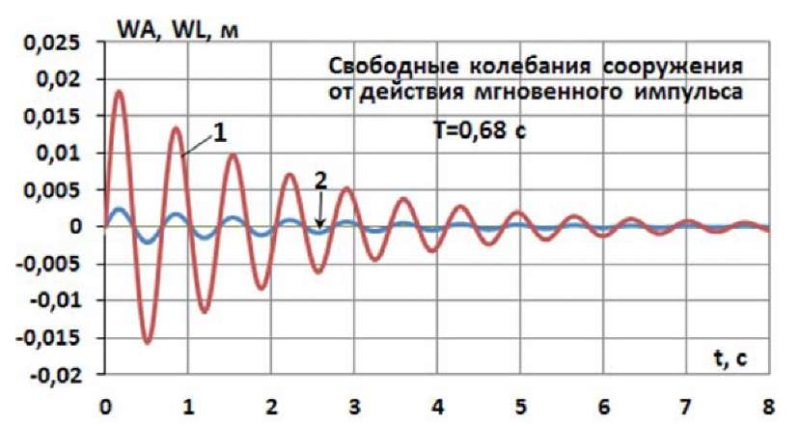
Рис. 3. Графики свободных колебаний
Fig. 3. Graphs of free vibrations
Из этих графиков следует, что период колебаний, полученный численным решением, совпадает с результатом (г).
На втором этапе на основе метода последовательных аппроксимаций исследуются колебания сооружения от действия землетрясения, представленного в виде заданной акселерограммы El Centro. На рис. 4 сравнивается ускорение, полученное для верхней точки сооружения, с графиком ускорения самого землетрясения. Видно, что относительное ускорение сооружения более чем в два раза превышает ускорение его основания.
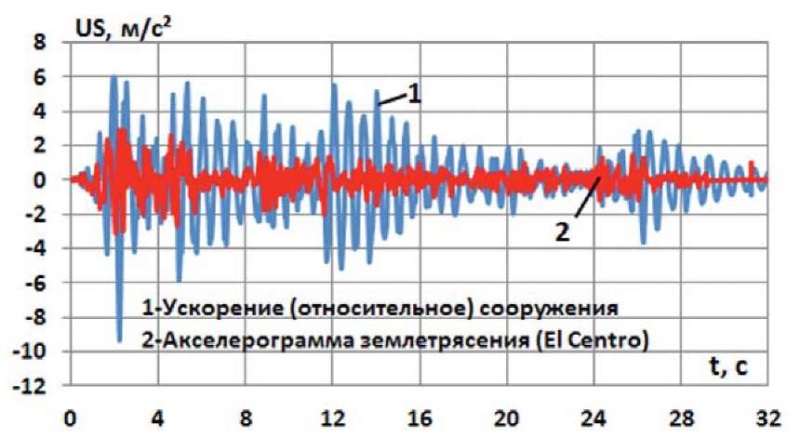
Рис. 4. Относительное ускорение верхней точки сооружения
(численное дифференцирование)
Fig. 4. Relative acceleration of the top point of the structure
(numerical differentiation)
Получены также результаты с применением алгоритма (28)–(30) и численного решения интеграла Дюамеля при τ = 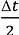 = 0,01 с
= 0,01 с
и ξ = 0,05. На рис. 5 для сопоставления приводятся аналогичные рис. 4 графики, полученные численным интегрированием. Можно заметить, что пиковые ускорения второго метода (рис. 5) несколько меньше, чем в первом методе (рис. 4), хотя характер изменения по времени практически совпадает. По-видимому, это объясняется тем, что шаг по времени в первом методе в два раза меньше, чем во втором.

Рис. 5. Относительное ускорение верхней точки сооружения
(численное интегрирование)
Fig. 5. Relative acceleration of the top point of the structure
(numerical integration)
На рис. 6 приведены графики перемещения верхней точки сооружения, полученные по первому (рис. 6а) и второму методам (рис. 6б). Сравнение показывает их практическое совпадение.
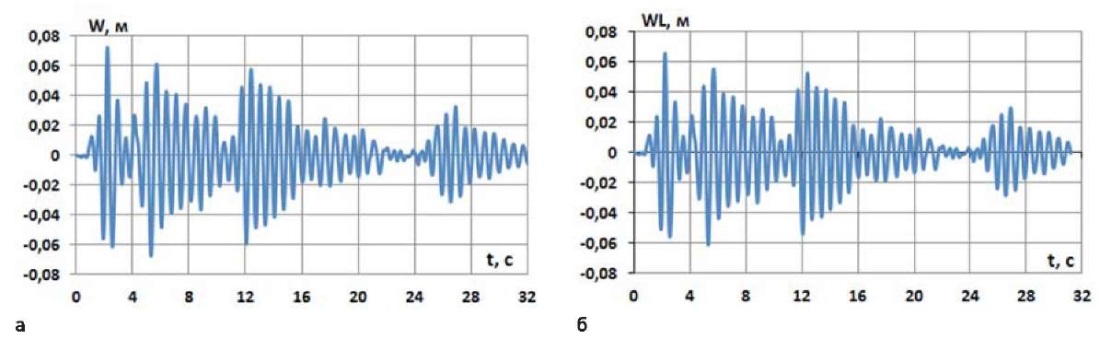
Рис. 6. Сравнение результатов по перемещениям, полученным двумя методами
Fig. 6. Comparison of displacement results obtained by the two methods
Вывод
Разработаны алгоритмы и компьютерные программы, которые позволяют исследовать динамические процессы, связанные с напряженно-деформированным состоянием сооружения, которое представляется в виде обобщенной системы, при различных воздействиях. Достоверность результатов подтверждается сравнением результатов, полученных двумя методами. Разработанные компьютерные программы могут быть использованы для проведения мониторинга уникальных объектов башенного типа.
Список литературы
1. Клейн Г.К., Рекач В.Г., Розенблат Г.И. Руководство к практическим занятиям по курсу строительной механики. Москва: Высшая школа; 1972.
2. Артоболевский И.И., Боголюбов А.Н., Болотин В.В., Волоховский В. Ю., Жинжер Н.И., Мишенков Г.В. Вибрации в технике. Справочник. Т. 1. Колебания линейных систем. Москва: Машиностроение; 1978.
3. Бидерман В.Л. Прикладная теория механических колебаний. Москва: Высшая школа; 1972.
4. Никитин Н.Н. Курс теоретической механики. Москва: Высшая школа; 1990.
5. Светлицкий В.А., Стасенко И.В. Сборник задач по теории колебаний. Москва: Высшая школа; 1973.
6. Яблонский А.А., Норейко С.С. Курс теории колебаний. Москва: Высшая школа; 1975.
7. Клаф Р., Пензиен Дж. Динамика сооружений. Москва: Стройиздат; 1979.
8. Двайт Г.Б. Таблицы интегралов и другие математические формулы. Москва: Наука; 1973.
9. Низомов Д.Н. Численные методы решения динамических задач строительной механики. Изв. АН Респ. Тадж. Отделение физико-математических, химических, геологических и технических наук. 1993;(1):62–72.
10. Низомо в Д.Н. Методы прямого интегрирования дифференциальных уравнений движения дискрет ных систем. В: Строительство и архитектура: сб. науч. тр. Таджикского технического университета. Душанбе: ТТУ; 1992. Вып. 2, с. 39–46.
11. Низомов Д.Н. Метод граничных уравнений в решении статических и динамических з адач строительной механики. Москва: Изд-во АСВ; 2000.
12. Низомов Д.Н., Каландарбеков И.К. Метод сосредоточенных деформаций. Душанбе: Дониш; 2015.
13. Дарков А.В., Шапиро Г.С. Сопротивление материалов. Москва: Высшая школа; 1969.
Об авторах
Д. Н. НизомовТаджикистан
Джахонгир Низомович Низомов, д-р техн. наук, профессор, член-корреспондент НАНТ, заведующий лабораторией сейсмостойкости зданий и сооружений
ул. Айни, д. 267, г. Душанбе, 734063, Республика Таджикистан
А. М. Сангинов
Таджикистан
Абдусамад Мирвафоевич Сангинов, канд. техн. наук, ведущий научный сотрудник лаборатории сейсмостойкости зданий и сооружений
ул. Айни, д. 267, г. Душанбе, 734063, Республика Таджикистан
М. М. Саломзода
Таджикистан
Муродбек Мухтор Саломзода, директор
ул. Хусейнзаде, д. 36а, г. Душанбе, 734025, Республика Таджикистан
Рецензия
Для цитирования:
Низомов Д.Н., Сангинов А.М., Саломзода М.М. Численное моделирование динамической задачи обобщенной системы с распределенными параметрами. Вестник НИЦ «Строительство». 2024;40(1):35-48. https://doi.org/10.37538/2224-9494-2024-1(40)-35-48. EDN: CYHKDR
For citation:
Nizomov D.N., Sanginov A.M., Salomzoda M.M. Numerical simulation of the dynamic problem of a generalized system with distributed parameters. Bulletin of Science and Research Center of Construction. 2024;40(1):35-48. (In Russ.) https://doi.org/10.37538/2224-9494-2024-1(40)-35-48. EDN: CYHKDR


























