Перейти к:
Свободные и вынужденные колебания балок под действием распределенной нагрузки
https://doi.org/10.37538/2224-9494-2024-2(41)-7-17
EDN: BRFAUI
Аннотация
Введение. Многолетний опыт проектирования и эксплуатации сооружений показывает, что для обеспечения их надежности недостаточно проведения только расчетов на прочность. Кроме обеспечения прочности и жесткости сооружений к ним часто предъявляются требования по учету влияния колебаний. Данные типы расчетов являются сложными, так как должно быть учтено большое количество самых различных факторов. В настоящее время сооружения все больше усложняются, и большое внимание уделяется расчетам на сейсмические воздействия на здания, что весьма актуально для районов строительства, где сейсмичность повышена. В инженерных сооружениях возникает повышенная напряженность, которая обусловливается этими и другими причинами. Свободные и вынужденные колебания различных упругих конструкций представляют несомненный возрастающий интерес и имеют обширную библиографию.
Цель настоящей статьи состоит в постановке полной математической задачи для двух наиболее распространенных способов закрепления концов балки, в определении спектров собственных частот и форм колебаний.
Материалы и методы. Рассматривается балка переменного сечения из однородного материала под действием поперечной распределенной нагрузки, которая совершает изгибные колебания. Свободные и вынужденные колебания описываются дифференциальными уравнениями. Сначала решается однородное уравнение, затем – неоднородное. Применен принцип Даламбера. Использован метод разделения переменных. Выполнены тестовые проверки.
Результаты. Получено дифференциальное уравнение в частных производных четвертого порядка с постоянными коэффициентами. Определены спектры собственных частот и форм колебаний. Высокая точность полученных результатов позволяет более коротким путем с наименьшим объемом вычислений определять характеристики свободных и вынужденных колебаний балок. Обнаружен интересный факт зависимости амплитуды и формы вынужденных колебаний стержней от близости частоты возмущений к собственным значениям и сдвига фаз компонентов векторного процесса возмущений.
Выводы. Выдвинуты гипотезы о существовании зависимости между коэффициентами затухания и линейно-вязкого трения материала, а также о постоянстве коэффициента затухания для всех собственных значений.
Ключевые слова
Для цитирования:
Барагунова Л.А., Шогенова М.М., Шогенов О.М., Жирикова И.А. Свободные и вынужденные колебания балок под действием распределенной нагрузки. Вестник НИЦ «Строительство». 2024;41(2):7-17. https://doi.org/10.37538/2224-9494-2024-2(41)-7-17. EDN: BRFAUI
For citation:
Baragunova L.A., Shogenova M.M., Shogenov O.M., Zhirikova I.A. Free and forced vibrations of beams under distributed load. Bulletin of Science and Research Center of Construction. 2024;41(2):7-17. (In Russ.) https://doi.org/10.37538/2224-9494-2024-2(41)-7-17. EDN: BRFAUI
Постановка краевой задачи
Однородный стержень (рис. 1) длины l с погонной массой m, с осевым моментом инерции поперечного сечения J, из материала с модулем упругости E под действием поперечной распределенной нагрузки q (x, t) совершает изгибные колебания, описываемые функцией u (x, t).
Изучению вынужденных колебаний, как правило, предшествует решение задачи о свободных колебаниях [1][2]. Математически это означает, что сначала решается однородное уравнение, затем – неоднородное. При свободных колебаниях поперечная нагрузка и другие возмущения отсутствуют, т. е. f (x, t) ≡ 0. Рассмотрим стержень переменного сечения из однородного материала, опирающийся по концам шарнирно (рис. 2). Такая задача имеет важное прикладное значение, так как она является базовой для всех других видов колебаний (вынужденных, кинематически возбуждаемых, параметрических и т. д.) [3–5].
Для вывода уравнения колебаний выделим элемент стержня длиной dx (рис. 3) и покажем все силы, приложенные к нему: M – изгибающий момент, Q – поперечная сила, dJ – даламберова сила инерции, dR – сила вязкого трения (демпфирования). Последние направлены вниз, являются следствием движения со скоростью и ускорением, направленными вверх, вычисляются по формулам
dI = müdx, dR = ηmudx.(1)
Здесь m = ρS;
ρ – плотность материала;
S – площадь поперечного сечения балки;
η – коэффициент демпфирования, точки над функциями означают дифференцирование по времени t.
По теории изгибных колебаний балок считается, что выделенный элемент стержня на рис. 3 принимается горизонтальным, а силы, приложенные к нему, – вертикальными.
Применяя принцип Даламбера, получим уравнение движения в виде равенства нулю суммы проекций всех сил на вертикальную ось
∑i Yi = 0, Q – Q – Q′dx + qdx – dI – dR = 0.(2)
Штрихи в индексах соответствуют дифференцированию по x. Из курса сопротивления материалов известно, что
Q = M′, M = EJu″.(3)
В уравнении (2) сократим Q, учтем (1), (3) и получим
– M″dx + qdx – müdx – ηmudx = 0.
Далее простейшие преобразования дают уравнение
(EJu″)″ + mü + ηmu = q(x, t),(4)
четвертого по переменной x, второго порядка по переменной t с переменными коэффициентами. При рассмотрении колебаний балки постоянного сечения из однородного материала уравнение (4) упрощается и приобретает вид уравнения в частных производных четвертого порядка, того же порядка, но с постоянными коэффициентами
EJuIV + mü + ηmu = q(x, t), uIV + γü + εu = f(x, t), x ∈ (0, l), t > – ∞.(5)
γ = m/EJ, f(x, t) = q(x, t)/EJ.
Здесь и далее IV в верхнем индексе обозначает четвертую производную по х. Уравнение (4) является основным уравнением колебаний балки. К нему необходимо присоединить дополнительные краевые условия: начальные, граничные.
Далее будут рассматриваться установившиеся колебания балки при гармонических возмущениях, которым будут соответствовать периодические решения. Поэтому начальные условия не потребуются, а граничные условия будут зависеть от способов опирания концов стержня и действующих здесь возмущений.
Уравнения (4), (5) являются дифференциальными уравнениями четвертого порядка по переменной x. Поэтому необходимо присоединить четыре граничных условия: по два на каждом конце балки.
Нетрудно заметить, что возмущения подразделяются на кинематические и динамические. Кинематическими являются возмущения в виде перемещений: линейных, угловых. Динамические возмущения представляются распределенными нагрузками, сосредоточенными силами и парами сил с моментами.
Пример постановки полной математической задачи покажем на двух наиболее распространенных способах закрепления концов балки.
1) Шарнирно-опертая балка (рис. 4). Возмущениями, действующими на такую балку, являются распределенная нагрузка q(x, t), вертикальные перемещения левого конца, моментная нагрузка, приложенная к шарниру левого конца, вертикальные перемещения правого конца, моментная нагрузка, приложенная к шарнирно-подвижному правому концу. Основное уравнение и граничные условия в совокупности образуют задачу
uIV + aü + εu• = f1(x, t), f1(x, t) = – q(x, t)/EJ x ∈ (0, l), t > – ∞.(6)
u(0, t) = f2(t), EJu″(0, t) = f3(t), u′(0, t) = f3(t),
u(l, t) = f4(t), EJu″(l, t) = f5(t).(7)
Знак минус в уравнении f1 учитывает противоположность между принятым в данной задаче направлением распределенной нагрузки и ее положительным направлением.
2) Балка, «заделанная» на левом конце и шарнирно опертая на правом конце (рис. 4).
Возмущения, действующие на такую балку, будут такими же, как и в предыдущем примере, за исключением f3(t). Здесь f3(t) – угловые перемещения левого конца балки. Основное уравнение колебания балки (6) остается без изменения, но граничные условия для этой балки уже другие
u(0, t) = f2(t), u′(0, t) = f3(t), u(l, t) = f4(t), EJu″(l, t) = f5(t).(8)
Заметим, что возмущения для обоих способов закрепления балки являются вектор-функцией с пятью компонентами.
f (x, t) = {f1 (t), f2 (t), f3 (t), f4 (t), f5 (t)}.(9)
Задача далее будет состоять в том, чтобы по заданной функции f (x, t) отыскать решение u (x, t).
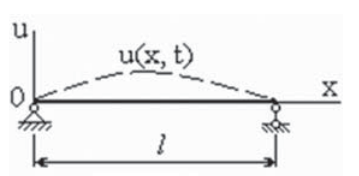
Рис. 1. Расчетная схема
Fig. 1. Design diagram
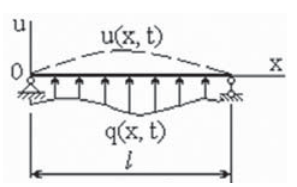
Рис. 2. Стержень под распределенной нагрузкой
Fig. 2. Beam under distributed load
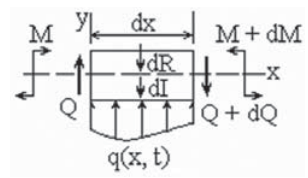
Рис. 3. Элемент стержня длиной dx
Fig. 3. Beam element with length dx
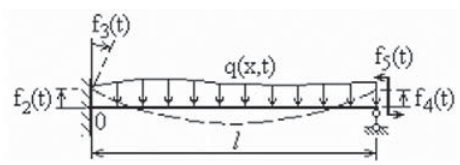
Рис. 4. Балка, «заделанная» на левом конце и опертая на правом конце
Fig. 4. Beam restrained on the left and supported on the right
Дифференциальное уравнение с постоянными коэффициентами
Свободные колебания рассмотрим для способов закрепления балки, показанных на рис. 3 и 4, в той же очередности.
1) Шарнирно-опертая балка.
Для свободных колебаний задача (6), (7) принимает вид
uIV + γü + εu = 0, x ∈ (0, l), t > – ∞.(10)
u(0, t) = 0, u″(0, t) = 0, u(l, t) = 0, u″(l, t) = 0.(11)
Эти условия означают, что в процессе колебаний концы балки не перемещаются в вертикальном направлении, и, как следствие шарнирного опирания, изгибающие моменты в концевых сечениях являются нулевыми.
Далее задача состоит в определении спектров собственных частот и форм.
С целью применения метода разделения переменных запишем
u(x, t) = X(x)T(t).(12)
Подставим (12) в (10) и получим
X IVT + γXT + εXT = 0,
разделим на произведение Х и Т и запишем результат
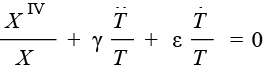 .(13)
.(13)
первое слагаемое зависит от х, а остальные два – от t. Поэтому уравнение (13) может быть верным лишь при выполнении условия
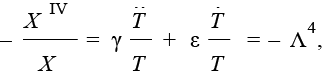 (14)
(14)
где Λ – некоторое число. Полученный результат содержит два уравнения. Рассмотрим второе равенство
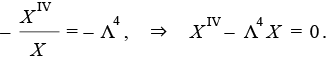 (15)
(15)
Подставляя (12) в (13), (14), находим граничные условия
X(0) = 0, X″(0) = 0, X(l) = 0, X″(l) = 0. (16)
Надо найти такое значение Λ, чтобы задача (15), (16) имела ненулевое решение. Это – задача Штурма – Лиувилля. Уравнение (15) имеет общее решение
X(x) = C1sinΛx + C2cosx + C3shΛx + C4chΛx.(17)
дважды дифференцируя, получим
X″(x) = Λ2 (– C1sinΛx – C2cosΛx + C3shΛx + C4chΛx). (18)
Первые два условия в (16) дают
C2 + C4 = 0, – C2 + C4 = 0 ⇒ C2 = C4 = 0.
Тогда (17), (18) упрощаются
X(x) = C1sinΛx + C3shΛx, X″(x) = Λ2 ( – C1sinΛx + C3shΛx).
С их учетом последние два условия в (16) принимают вид
C1sinΛl + C3shΛl = 0, – C1sinΛl + C3shΛl = 0.(19)
Приравниваем определитель системы уравнений к нулю, чтобы получить нетривиальное решение задачи, и приходим к трансцендентному уравнению
2sinΛl shΛl = 0.(20)
Если shΛl = 0, то Λl = 0 ⇒ X(x) = 0.
Это решение тривиальное, и оно соответствует равновесному состоянию при отсутствии колебаний. Интерес представляют нетривиальные решения, соответствующие колебаниям. Поэтому приравниваем к нулю другой сомножитель в левой части (20)
 .(21)
.(21)
Из (20)
shΛl ≠ 0, sinΛl = 0 ⇒ C3 = 0.
Окончательно для формы колебаний имеем
X(x) = C1sinΛkx, k = 1, 2, …
Без постоянного сомножителя эти функции представляют собой спектр собственных функций колебаний
φk(x) = sinΛkx, k = 1, 2, …(22)
Обратимся к первому из уравнений (14) и запишем его в виде
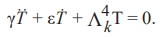 .(23)
.(23)
Его характеристическое уравнение
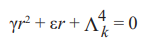 (24)
(24)
имеет корни
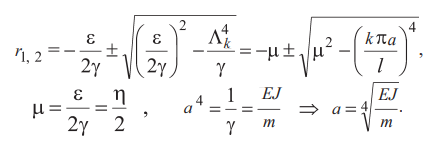
Обычно μ2 < Λ4. Поэтому можно записать
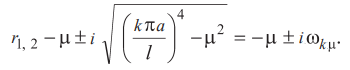
Здесь обозначено
ωkμ= k = 1, 2, …(25)
Решения уравнения (23) имеют вид
Tk(t) = e–μt (Akcosωkμt + Bksinωkμt), k = 1, 2, …(26)
В силу (26) формулы (25) определяют спектры собственных частот. Первая – при наличии сил трения, вторая – при их отсутствии.
Спектры собственных частот и форм могут быть найдены и другим, более легким способом [6–8]. С этой целью учтем затухающий характер свободных колебаний балки и запишем решение задачи (10), (11) в виде
u(x, t) = X(x) ert.(27)
Здесь
r = – μ + iω, μ > 0, ω > 0, (28)
r – характеристический показатель;
μ и ω – подлежащие определению коэффициент затухания и частота свободных колебаний.
Подстановка (27) в (10), (11) дает
X IV + (γr2 + εr)X = 0, X(0) = 0, X(l) = 0. (29)
Введем обозначение
d4 = – γr 2 – εr (30)
и перепишем задачу (29) в виде
X IV – d 4X = 0, X(0) = 0, X″(0) = 0, X(l) = 0, X″(l) = 0.(31)
Задачи (15), (16) и (31) совпадают с точностью до обозначения коэффициентов Λ и d. Следовательно, по аналогии с (24) можно записать
d = dk = , k ∈ N. γr 2 + εr + d 4 = 0.
Полученное уравнение совпадает с характеристическим уравнением (27), значит, мы пришли к тому же решению, но более коротким путем.
2) Балка, «заделанная» на левом конце и свободно опертая на правом.
Для такой балки при f(t) ≡ 0 задача принимает вид
uIV + γü + εu• = 0, x ∈ (0, l), t > – ∞,(32)
u(0, t) = 0, u′(0, t) = 0, u(l, t) = 0, u″(l, t) = 0, t > – ∞. (33)
Повторение предыдущих выкладок приводит к новой системе уравнений относительно произвольных постоянных, из которой следует
C2 = C4 = 0, C1sinΛl + C3 shΛl = 0, C1cosΛl + C3 chΛl = 0.
Условие существования нетривиального решения этой системы дает уравнение частот
tgΛl = thΛl.
Это уравнение трансцендентное, решение можно получить только в приближенной форме. Следующая формула дает ненулевые корни этого уравнения с довольно большой точностью
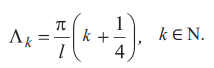
При k = 1 погрешность составляет около 0,5 %, с увеличением k погрешность очень быстро стремится к нулю.
После повторения процедуры предыдущего примера получаем
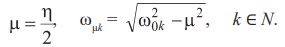 (34)
(34)
Здесь
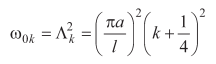
ω0k – частоты свободных колебаний при отсутствии трения, ωμk – то же при наличии трения.
Собственные функции колебаний, соответствующие каждой частоте, имеют вид
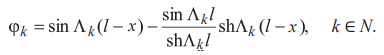 . (35)
. (35)
Пример 1. Стальная балка изготовлена из двутавра № 14 длиной l = 6 м. Численные характеристики принятой балки: удельная плотность стали ρ = 7800 кг/м 3, модуль упругости E = 200 ГПа, площадь поперечного сечения S = 17,4 см 2, момент инерции сечения J = 572 см4, η = 1 с–1.
Определим первые три элемента спектров собственных значений и функций для рассмотренных двух случаев закрепления концов балки.
Погонная масса и коэффициент уравнения колебаний
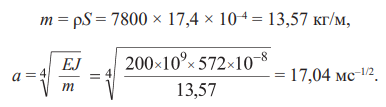
Вычисления по формулам (25) и (34) дают спектры собственных значений: для шарнирно-опертой балки (значения в скобках при отсутствии трения)
ωkμ (ωk0) = {79,59 (79,60), 318,38 (318,38), 716,36 (716,36), …} c–1,
для балки с защемленным левым и шарнирно-опертым правым концом
ωkμ (ωk0) = {124,35 (124,36), 402,95 (402,95), 840,73 (840,73), …} c–1.
Элементы спектра собственных функций определяются по формулам (22) и (35).
Вычисления и графики, выполненные на компьютере, представлены кривыми на рис. 5 и 6. Номера кривых соответствуют коэффициентам k в формулах (9) и (10).
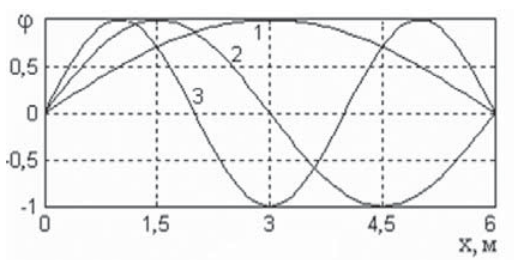
Рис. 5. Собственные функции колебаний
Fig. 5. Eigenfunctions of vibrations
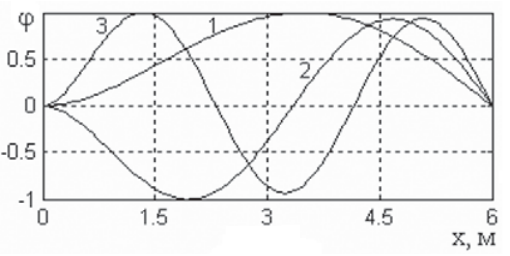
Рис. 6. Спектр собственных функций
Fig. 6. Spectrum of eigenfunctions
Список литературы
1. <i>Бабаков И.М.</i> Теория колебаний. Москва: Наука, глав. ред. физ.-мат. лит.; 1968.
2. <i>Бидерман В.Л.</i> Прикладная теория механических колебаний. Москва: Высшая школа; 1979.
3. <i>Масленников А.М.</i> Динамика и устойчивость сооружений. Москва: Издательство Юрайт; 2016.
4. <i>Амосов А.А., Синицын С.Б.</i> Основы теории сейсмостойкости сооружений. Москва: Издательство АСВ; 2001.
5. <i>Амосов А.А., Синицын С.Б.</i> Основы теории сейсмостойкости сооружений. Москва: Издательство АСВ; 2010.
6. <i>Формалев В.Ф., Ревизников Д.Л.</i> Численные методы. Изд. 2-е. Москва: Физматлит; 2006.
7. <i>Золотов А.Б., Акимов П.А., Сидоров В.Н.</i> Математические методы в строительной механике (с основами теории обобщенных функций). Москва: Издательство АСВ; 2008.
8. <i>Kulterbayev Kh.P., Shogenova M.M., Baragunova L.A.</i> On the Influence of the Characteristic Frequency and Broadband of Seismic Effects on the Vertical Rod Oscillations. IOP Conference Series: Materials Science and Engineering. 2020;753(3):042040. https://doi.org/10.1088/1757-899x/753/4/042040
9. <i>Культербаев Х.П., Чеченов Т.Ю., Барагунов Т.М.</i> Вынужденные колебания континуально-дискретной многопролетной балки при учете инерционных сил вращения. Вестник ВолгГАСУ. Серия: Строительство и архитектура. 2012;(26):48–55.
10. <i>Культербаев Х.П.</i> Основы теории колебаний. Основы теории, задачи для домашних заданий, примеры решений. Нальчик: Кабардино-Балкарский государственный университет им. Х.М. Бербекова; 2003.
Об авторах
Л. А. БарагуноваРоссия
Лялюся Адальбиевна Барагунова, старший преподаватель кафедры строительных конструкций и механики
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
e-mail: baragunoval@mail.ru
тел.: +7 (928) 075-62-99
М. М. Шогенова
Россия
Марьяна Мухарбиевна Шогенова, канд. ф.-м. наук, доцент, доцент кафедры строительных конструкций и механики
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
e-mail: shogenova_mar@mail.ru
тел.: +7 (928) 710-50-45
О. М. Шогенов
Россия
Олег Мухамедович Шогенов, канд. техн. наук, доцент, доцент кафедры строительных конструкций и механики
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
e-mail: shogenova_mar@mail.ru
тел.: +7 (928) 705-59-16
И. А. Жирикова
Россия
Инна Аликовна Жирикова, старший преподаватель кафедры строительного производства
ул. Чернышевского, д. 173, г. Нальчик, 360004, Российская Федерация
e-mail: innazh94@mail.ru
тел.: +7 (988) 720-22-16
Рецензия
Для цитирования:
Барагунова Л.А., Шогенова М.М., Шогенов О.М., Жирикова И.А. Свободные и вынужденные колебания балок под действием распределенной нагрузки. Вестник НИЦ «Строительство». 2024;41(2):7-17. https://doi.org/10.37538/2224-9494-2024-2(41)-7-17. EDN: BRFAUI
For citation:
Baragunova L.A., Shogenova M.M., Shogenov O.M., Zhirikova I.A. Free and forced vibrations of beams under distributed load. Bulletin of Science and Research Center of Construction. 2024;41(2):7-17. (In Russ.) https://doi.org/10.37538/2224-9494-2024-2(41)-7-17. EDN: BRFAUI


























