Перейти к:
Совершенствование расчетов соединений анизотропных конструкционных материалов
https://doi.org/10.37538/2224-9494-2024-2(41)-69-78
EDN: HUYCFE
Аннотация
Введение. Современные методы проектирования и расчета строительных конструкций часто ограничиваются упругой стадией работы материалов. Для анализа напряженно-деформированного состояния соединений необходимо учитывать свойства материала, а также его работу под нагрузкой, включая как упругие, так и нелинейные стадии. Значительный интерес представляют анизотропные материалы, такие как древесина. Теоретическое и практическое исследование работы деревянных образцов представлено в данной работе.
Целью данной работы является выполнение натурных испытаний и численное моделирование для анализа напряженно-деформированного состояния и совершенствования расчетов анизотропных конструкционных материалов.
Материалы и методы. Выполнены натурные испытания деревянных образцов из сосны второго сорта на сжатие вдоль волокон с фиксацией вертикальных напряжений сжатия и деформаций. Испытания выполнены на гидравлическом прессе с максимальной нагрузкой 50 т. Для фиксации деформаций и напряжений использовалось тензометрическое оборудование. На основе данных натурных испытаний выполнено численное моделирование образцов в программных комплексах ЛИРА-САПР и ANSYS.
Результаты. Согласно результатам натурных испытаний, упругая стадия работы древесины при сжатии находится в диапазоне до 90 кН, после чего наблюдается переход к пластической деформации. Выполнено численное моделирование образцов в программных комплексах ЛИРА-САПР и ANSYS, которое показало сходимость результатов. Однако программный комплекс ANSYS позволяет более детально моделировать и рассчитывать соединения и конструкции. Сравнение распределений вертикальных напряжений сжатия σy, полученных в результате натурных испытаний и численного моделирования в программном комплексе ANSYS, показало сходимость результатов (невязка не превышает 5 %). Это подтверждает эффективность использования данного программного комплекса для моделирования соединений анизотропных материалов.
Выводы. Результаты натурных испытаний и численного моделирования показали эффективность применения программного комплекса ANSYS для расчета сложных соединений анизотропных конструкционных материалов. Сходимость результатов достигнута для упругой стадии. Для моделирования пластической стадии необходимы дополнительные исследования.
Для цитирования:
Колесников Н.В., Арискин М.В., Мартышкин Д.О., Меркушов А.В. Совершенствование расчетов соединений анизотропных конструкционных материалов. Вестник НИЦ «Строительство». 2024;41(2):69-78. https://doi.org/10.37538/2224-9494-2024-2(41)-69-78. EDN: HUYCFE
For citation:
Kolesnikov N.V., Ariskin M.V., Martyshkin D.O., Merkushov A.V. Improved calculations of joints in anisotropic structural materials. Bulletin of Science and Research Center of Construction. 2024;41(2):69-78. (In Russ.) https://doi.org/10.37538/2224-9494-2024-2(41)-69-78. EDN: HUYCFE
Введение
Благодаря развитию научно-технического прогресса, усовершенствованию мощности и производительности электронно-вычислительных машин (ЭВМ), а также развитию и доступности расчетных программных комплексов стало доступно моделирование сложных соединений анизотропных конструкционных материалов. Наиболее распространенным является создание объемных конечно-элементных моделей конструкций и соединений в программных комплексах (ПК) ЛИРА-САПР и ANSYS [1–3].
Для анализа напряженно-деформированного состояния (НДС) соединения при нагружении необходимо рассматривать упругие и нелинейные стадии работы материала. В современной практике строительства расчет соединений и конструкций производится в упругой стадии без учета пластических деформаций.
Далее на основе натурных испытаний и численного моделирования рассмотрим стадии работы материала.
Экспериментальная часть
Для определения данных стадий необходимо провести натурные испытания образцов. Для этого были изготовлены деревянные бруски с размерами 50 × 50 × 200 (h) мм из сосны второго сорта.
Испытания производились на гидравлическом прессе П-500 (рис. 1а). Нагружение образцов производилось непрерывно со скоростью 2 кН/мин. Для равномерного распределения нагрузки на торец образца устанавливалась дополнительная оснастка (рис. 1а). Для определения нормальных напряжений сжатия на поверхность образцов наклеены тензорезисторы, подключенные к комплекту для тензометрии (рис. 1б). Испытания проводились до полного разрушения образцов (рис. 1в).
Специфика оборудования предполагает собой нагружение образца до величины 5 кН, после чего нагружение производится непрерывно, с изначально заданной скоростью. Фиксация напряжения производилась после приложения нагрузки в 5 кН, что необходимо учитывать при построении графиков нормальных напряжений, полученных при численном моделировании.
Графики относительных деформаций образцов представлены на рис. 2, согласно которому упругая стадия работы материала находится в диапазоне до 90 кН, в связи с чем напряжения сжатия образцов рассматриваем в упругой стадии.
Далее рассмотрим методику создания объемных конечно-элементных моделей в программных комплексах ANSYS и ЛИРА-САПР.
В ПК ANSYS образец замоделирован как объемное тело (solid), которому были заданы свойства древесины, учитывающие ортотропию материала. Нижняя грань образца зафиксирована через граничные условия опоры типа fixed support (жесткое защемление) (рис. 3а). У верхней грани образца замоделирована стальная пластина, на которую приложена вертикальная нагрузка, по аналогии с натурными испытаниями. Контакт между поверхностями древесины и стали определен как bonded (моделирование жесткого клеевого соединения). Следует отметить, что всплесками напряжения в углах образца можно пренебречь (рис. 3а), так как в реальном образце напряжения возникают равномерно по всему объему тела.
В ПК ЛИРА-САПР брусок замоделирован объемными конечными элементами КЭ 36, которому присвоены характеристики древесины, учитывающие ортотропию материала в местной системе координат. В узлах нижней грани образца заданы связи, ограничивающие перемещения вдоль оси z, и связи по трем углам, дополнительно огранивающие перемещения по осям x, y и xy (рис. 3б). Нагрузка приложена к узлам верхней грани через систему условных единиц, учитывающих грузовую площадь каждого узла, для исключения деформации верхних углов образца.
Для достижения сходимости результатов натурных испытаний и численного моделирования образцов были введены корректирующие коэффициенты, учитывающие реальный модуль упругости материала, также для сопоставления результатов был определен коэффициент чувствительности тензорезисторов.
Для оценки результатов испытаний и моделирования было проведено определение фактического модуля упругости древесины на основе испытаний на четырехточечный изгиб брусков размерами 30 × 30 × 200 мм (рис. 4). Проведенные испытания образцов показали значения определяемых характеристик, близкие к значениям, приведенным в СП 64.13330.2017 [4]. На этом основании при моделировании и расчете принимались табличные значения расчетных характеристик древесины сосны второго сорта.
Далее представлены результаты расчета в ПК ANSYS и ЛИРА-САПР: перемещения и напряжения сжатия (рис. 5–7).
По результатам численного моделирования образцов (рис. 5–7) установлена сходимость полученных данных (погрешность не превышает 5 %) при нагружении образцов сосредоточенной нагрузкой 25–30 кН. Для дальнейшего изучения соединений конструкций и материалов мы будем использовать программный комплекс ANSYS. Этот комплекс имеет обширную базу данных, которая позволяет выполнять моделирование различных клеевых соединений, учитывать трение материала, возможность ступенчатого и длительного нагружения.
На основе результатов натурных испытаний и компьютерного моделирования образцов построены графики распределения вертикальных напряжений сжатия σy (рис. 7). Как отмечено ранее, специфика оборудования предполагает собой нагружение образца до величины 5 кН, что отображено на рис. 7.
Согласно рис. 7, установлена сходимость результатов натурных испытаний и компьютерного моделирования (погрешность не превышает 5 %), что подтверждает правильность создания объемной конечно-элементной модели образцов.
Для моделирования пластической работы материала и соединения необходимы дополнительные исследования, введение дополнительных коэффициентов, задание дополнительных контактных связей, то есть моделирование образцов с применением теории разрушения. На данной стадии моделирования соединения конструкций рассматриваются в упругой стадии работы материала.

Рис. 1. Испытание деревянных образцов на сжатие: а – образец в прессе П-500; б – общий вид образца;
в – общий вид разрушения образца
Fig. 1. Compression tests of wooden samples: а – sample in the P-500 press; b – general view of the sample;
с – general view of the sample destruction
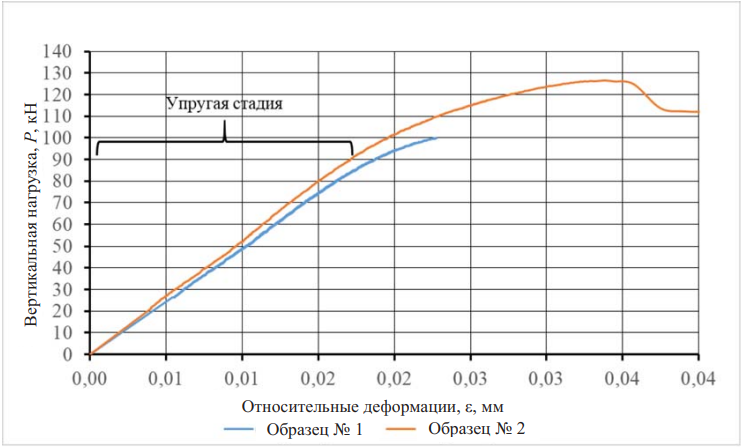
Рис. 2. Относительные деформации образца
Fig. 2. Sample strain
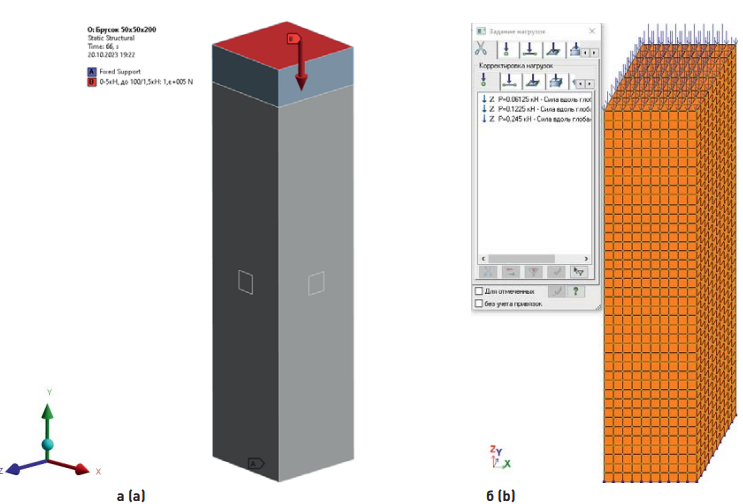
Рис. 3. Объемная конечно-элементная модель образца в ПК ANSYS (а) и ЛИРА-САПР (б)
Fig. 3. Volumetric finite element model of the sample in the ANSYS SP (а) and LIRA-SAPR SP (b)

Рис. 4. Испытание деревянных образцов на четырехточечный изгиб
Fig. 4. Four point bend testing of wooden samples
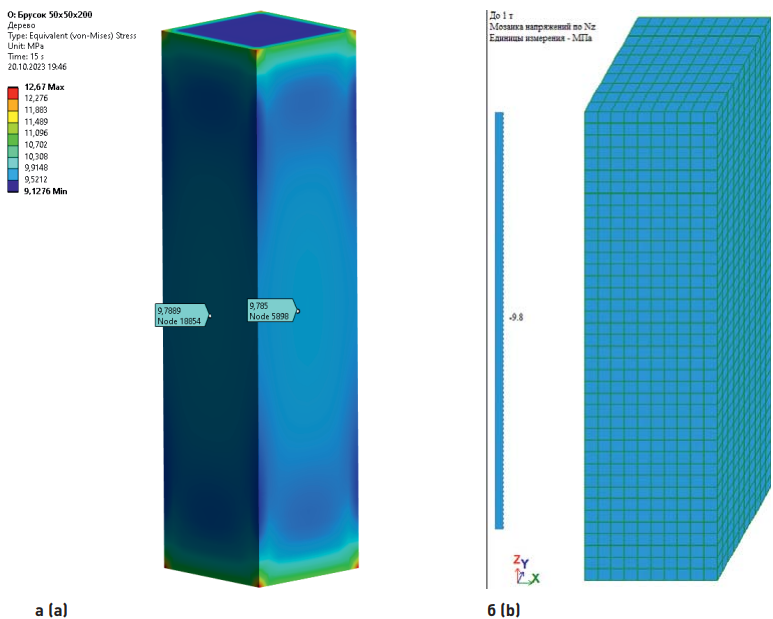
Рис. 5. Вертикальные напряжения сжатия при нагрузке 25 кН в ПК ANSYS (а) и ЛИРА-САПР (б)
Fig. 5. Vertical compression stresses at a load of 25 kN in the ANSYS SP (а) and LIRA-SAPR SP (b)
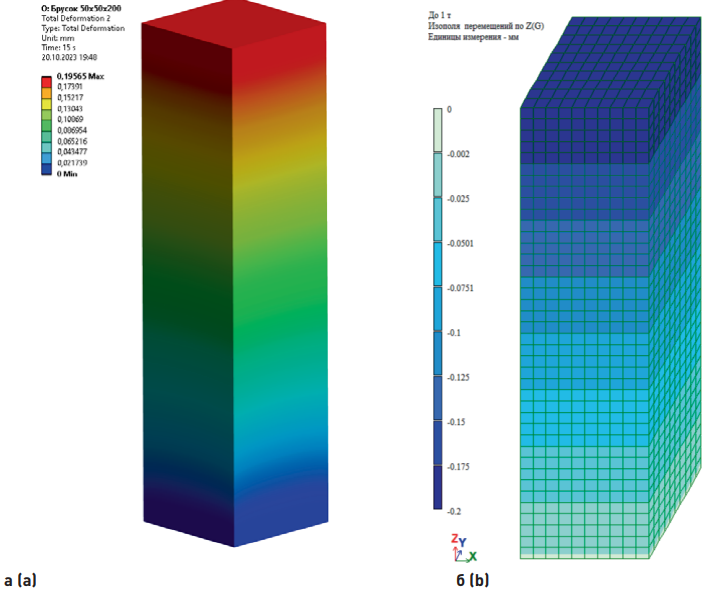
Рис. 6. Вертикальные перемещения при нагрузке 25кН в ПК ANSYS (а) и ЛИРА-САПР (б)
Fig. 6. Vertical movements at a load of 25kN in the ANSYS SP (a) and LIRA-SAPR SP (б)
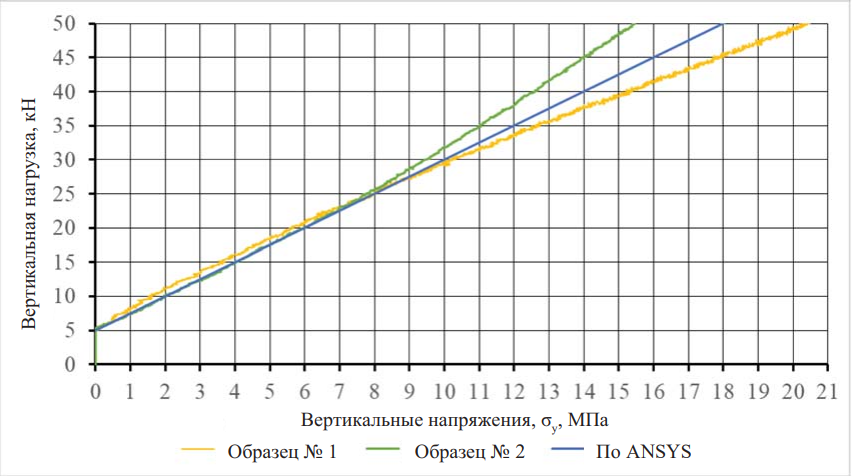
Рис. 7. Графики распределения вертикальных напряжений сжатия σy
Fig. 7. Plots of the vertical compression stress distribution σy
Заключение
Результаты исследования подтвердили эффективность применения программного комплекса ANSYS для моделирования сложных соединений анизотропных конструкционных материалов. Это подтверждается сходимостью данных, полученных в ходе натурных испытаний деревянных брусков из сосны второго сорта, и данных, полученных в ходе компьютерного моделирования.
Важно отметить, что эта сходимость была достигнута для упругой стадии работы материала, моделирование пластической стадии требует дальнейших исследований.
Моделирование соединений анизотропных конструкционных материалов с учетом их особенностей не только позволяет сократить расходы на создание и тестирование образцов, но и открывает возможности для оптимизации процесса проектирования. На этапе моделирования можно корректировать геометрию элементов, свойства материалов, режим испытания, выявлять и устранять недочеты конструкции, что в конечном итоге приводит к более эффективному использованию ресурсов.
Список литературы
1. <i>Данилов В.М., Ерофеев А.В., Горохов Т.И.</i> Возможности программного комплекса ANSYS для решения научно-практических задач в строительстве. В: Молодые ученые – развитию национальной технологической инициативы (Поиск 2021). С б. материалов Национальной (с международным участием) молодежной науч.-техн. конф. Иваново: ИВГПУ; 2021, с. 182–185.
2. <i>Мартыненко Т.М., Пронкевич С.А., Мартыненко И.М., Максимович В.А.</i> Анализ прочности узловых соединений при различных исполнениях конструкции на основе моделирования в среде ANSYS. В: Механика исследования и инновации. Междунар. сб. науч. ст. Вып. 15. Гомель; 2022, с. 147–151.
3. <i>Козлов Д.В., Муйземнек А.Ю., Гуськов М.С.</i> Варианты упрощения модели расчета композиционного материала в программном комплексе ANSYS. В: Информационные технологии в науке и образовании. Проблемы и перспективы. Сб. ст. по материалам VIII Всероссийской межвузовской науч.-практ. конф. Пенза: ПГУ; 2021, с. 362–363.
4. СП 64.13330.2017. Деревянные конструкции. Актуализированная редакция СНиП II-25-80 [интернет]. Режим доступа: https://docs.cntd.ru/document/456082589.
5. <i>Шемякин Е.И., Тутурин С.В., Короткина М.Р.</i> Разрушение древесины при сжатии. Вестник МГУЛ – Лесной Вестник. 2005;(3):56–70.
6. <i>Морозов Е.М., Муйземнек А.Ю., Шадский А.С.</i> ANSYS в руках инженера: Механика разрушения. 2-е изд. Москва: ЛЕНАНД; 2010.
Об авторах
Н. В. КолесниковРоссия
Никита Викторович Колесников, аспирант кафедры строительных конструкций
ул. Германа Титова, д. 28, г. Пенза, 440028, Российская Федерация
e-mail: ko1esnikov.1998@list.ru
М. В. Арискин
Россия
Максим Васильевич Арискин, канд. техн. наук, доцент кафедры строительных конструкций
ул. Германа Титова, д. 28, г. Пенза, 440028, Российская Федерация
e-mail: m.v.ariskin@mail.ru
Д. О. Мартышкин
Россия
Даниил Олегович Мартышкин, аспирант кафедры строительных конструкций
ул. Германа Титова, д. 28, г. Пенза, 440028, Российская Федерация
e-mail: historical95@mail.ru
А. В. Меркушов
Россия
Антон Викторович Меркушов, аспирант кафедры строительных конструкций
ул. Германа Титова, д. 28, г. Пенза, 440028, Российская Федерация
e-mail: merkushov.av@mail.ru
Рецензия
Для цитирования:
Колесников Н.В., Арискин М.В., Мартышкин Д.О., Меркушов А.В. Совершенствование расчетов соединений анизотропных конструкционных материалов. Вестник НИЦ «Строительство». 2024;41(2):69-78. https://doi.org/10.37538/2224-9494-2024-2(41)-69-78. EDN: HUYCFE
For citation:
Kolesnikov N.V., Ariskin M.V., Martyshkin D.O., Merkushov A.V. Improved calculations of joints in anisotropic structural materials. Bulletin of Science and Research Center of Construction. 2024;41(2):69-78. (In Russ.) https://doi.org/10.37538/2224-9494-2024-2(41)-69-78. EDN: HUYCFE


























