Перейти к:
Расчет глубины сезонного промерзания грунтов инженерными и численными методами
https://doi.org/10.37538/2224-9494-2024-3(42)-56-82
EDN: RSJSVQ
Аннотация
Введение. Суровые климатические условия Российской Федерации предопределяют сезонное промерзание грунта и развитие криогенных процессов, негативно влияющих на фундаменты и заглубленные сооружения. Величина сил морозного пучения существенно зависит от глубины промерзания грунта, что делает оценку глубины промерзания грунта весьма актуальной.
Цель. Расчет и оценка глубины сезонного промерзания грунтов инженерными и численными методами.
Материалы и методы. Выполнялись расчеты глубины промерзания грунта по двум площадкам, сложенным супесями и суглинками. Инженерные расчеты выполнялись по четырем методикам, изложенным в следующих нормативных документах: «Рекомендации по теплотехническим расчетам и прокладке трубопроводов в районах с глубоким сезонным промерзанием грунтов», «Справочник по строительству на вечномерзлых грунтах», «Рекомендации по учету и предупреждению деформаций и сил морозного пучения грунтов», «Рекомендации по прогнозу теплового состояния мерзлых грунтов», а численные – в программных комплексах Frost 3D и Борей 3D. Экспериментальные площадки расположены в Тымовском районе Сахалинской области, где прокладывался трубопровод Сахалин‑2.
Результаты. Результаты исследований показали, что инженерные методики дают завышенные результаты при использовании в оценке искомой глубины промерзания грунта большого спектра климатических и грунтовых параметров: температура воздуха, высота и плотность снежного покрова, скорость ветра, коэффициенты конвективного теплообмена, суммарная солнечная радиация, альбедо поверхности, максимальная упругость водяных паров и др. В то же время использование формулы Стефана с ограниченным набором входных параметров дает близкие по значениям результаты. Численные методы показали близкие результаты между собой, но на 32–47 % больше, чем результаты инженерных расчетов при оголенной поверхности грунта.
Выводы. Предлагается проведение научных исследований динамики изменения глубины промерзания грунта в полевых условиях и сопоставление с результатами инженерных и численных расчетов для совершенствования данных методик.
Ключевые слова
Для цитирования:
Алексеев А.Г. Расчет глубины сезонного промерзания грунтов инженерными и численными методами. Вестник НИЦ «Строительство». 2024;42(3):56-82. https://doi.org/10.37538/2224-9494-2024-3(42)-56-82. EDN: RSJSVQ
For citation:
Alekseev A.G. Calculation of seasonal soil freezing depth by engineering and numerical methods. Bulletin of Science and Research Center of Construction. 2024;42(3):56-82. (In Russ.) https://doi.org/10.37538/2224-9494-2024-3(42)-56-82. EDN: RSJSVQ
Территория Российской Федерации содержит различные климатические и геологические зоны, характеризующиеся различными свойствами, но, несмотря на это, практически вся подвержена сезонному промерзанию грунта. Промерзание грунта вызывает развитие морозного пучения влажных песчаных и глинистых грунтов, приводя к деформированию поверхности грунта и сооружений, расположенных в промерзающем грунте. Прогнозирование глубины и скорости промерзания грунта в условиях изменения климата и неоднородности грунтов является важной научно-практической задачей [1–12].
Имеющиеся на сегодня инженерные методы нашли отражение в нормативной документации как федерального [13][14], так и отраслевого уровня [15–18], кроме того, разработаны и успешно применяются несколько российских программных комплексов, в меньшей степени – зарубежных [1]. На глубину промерзания влияют факторы климатического направления (температура воздуха, высота и плотность снежного покрова, скорость ветра, коэффициенты конвективного теплообмена, суммарная солнечная радиация, альбедо поверхности, максимальная упругость водяных паров и др.), а также геологические параметры (тип грунта в разрезе, физические и теплофизические свойства грунта). Определение данных параметров вызывает трудности, что в конечном счете влияет на результат. Поэтому выбор эффективного метода оценки величины глубины промерзания, опирающийся на базовый, легко определяемый набор входных параметров, является актуальным вопросом.
Анализ эффективности определения сезонного промерзания грунтов выполнялся на основе расчетов по четырем инженерным методикам и в двух программных комплексах. Расчеты велись для Тымовского района Сахалинской области, где прокладывался трубопровод Сахалин-2. Выполнялись расчеты для оголенной поверхности и поверхности грунта, находящейся под слоем снега, для двух типов грунта: супеси текучей (ПК1181 и 1190) и суглинка мягкопластичного (ПК1185 и 1202+50).
Инженерный расчет глубины промерзания грунта под слоем снега велся по четырем источникам: «Рекомендации по теплотехническим расчетам и прокладке трубопроводов в районах с глубоким сезонным промерзанием грунтов» [15]; «Справочник по строительству на вечномерзлых грунтах» [16]; «Рекомендации по учету и предупреждению деформаций и сил морозного пучения грунтов» [17]; «Рекомендации по прогнозу теплового состояния мерзлых грунтов» [18], а также в двух программных комплексах – Frost 3D и Борей 3D.
1. Расчет глубины сезонного промерзания грунтов по «Рекомендациям по теплотехническим расчетам и прокладке трубопроводов в районах с глубоким сезонным промерзанием грунтов» [15]
1.1. Расчеты для пикетов ПК1181 и 1190
1.1.1. Исходные данные
В связи с тем, что метеорологические данные наблюдений за период не менее 10 лет для данного района – Тымовского (Сахалинская область) отсутствуют, данные о температуре воздуха приняты по близлежащему району острова Сахалин – г. Кировское. Высота снежного покрова принята различной, для сравнительного анализа: hc = 0; 0,14; 1,12 и 1,58 м.
На данных пикетах ПК1181 и 1190 с поверхности залегают супеси текучие, имеющие следующие физические характеристики: W = 0,339; Wl = 0,286; Wp = 0,232; Ip = 5,4; IL > 1; ρ = 1,66 г/см³; ρd = 1,20 г/см³; ρs = 2,69 г/см³; e = 1,24; Sr = 0,81.
Расчетные значения коэффициентов тепловодности и объемной теплоемкости мерзлого и талого грунтов λf, Cf и λth, Cth принимались по [13] в зависимости от плотности минерального скелета грунта ρd и суммарной влажности грунта Wtot.
Суммарная влажность грунта Wtot для участков, где предусматривается вертикальная планировка местности согласно [15] п. 2.2.13 для суглинков и супесей, принималась равной Wtot ≈ Wр.
Тогда для супеси при Wtot = Wр = 0,232 и ρd = 1,20 г/см³ коэффициенты тепловодности и объемной теплоемкости равны:
для мерзлого грунта: λf = 1,80 Вт/м °C = 1,54 ккал/мч °C; Cf = 2100 кДж/м³ °C = 500 ккал/м³ °C;
для талого грунта: λth = 1,71 Вт/м °C = 1,48 ккал/мч °C; Cth= 2945 кДж/м³ °C = 701 ккал/м³ °C.
Величина удельной теплоты замерзания воды (таяния льда) в единице объема грунта определяется в соответствии с [13] по формуле:
Zv = Z0 (Wtot – Ww)ρd, (1)
где Z0 = 3,35 × 10 4 Дж/н (80 ккал/кг) – скрытая теплота плавления льда (замерзания воды);
ρd – плотность сухого грунта (скелета грунта), кг/м³;
Ww – весовое содержание незамерзшей воды при данной температуре грунта, д. е. Приближенно Ww для незасоленного грунта можно принять равным:
Ww = KнWp, (2)
где Wp – влажность на границе пластичности (раскатывания), д. е.;
Kн – коэффициент, принимаемый по [13] в зависимости от числа пластичности грунта Ip и температуры грунта Т, °C.
Температуру грунта можно определить следующим образом:
Т = 0,4 Тсз, (3)
где Тсз – среднезимняя температура воздуха (для г. Кировское по СНиП 23-01-99 «Строительная климатология» [19] Тсз = –13,9 °C).
Тогда Т = 0,4 Тсз = 0,4 × (–13,9) = –5,56 °C, по [13] Кн = 0,28.
Ww = КнWp = 0,28 × 0,232 = 0,065.
Величина удельной теплоты замерзания воды (таяния льда) в единице объема грунта составила:
Zv = Z0 (Wtot – Ww)ρd = 3,35 × 10 4(0,232–0,065) × 12 000 = 6,7 × 10 7 Дж/м³.
1.1.2. Методика расчета
Глубина сезонного промерзания грунта, Нм, определяется по формуле:
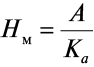 , (4)
, (4)
где Ка – параметр, вычисляемый из выражения:
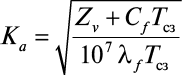 , (5)
, (5)
А – коэффициент, определяемый [15] в зависимости от приведенной температуры θ при значении τ, равной максимальной продолжительности зимнего периода;
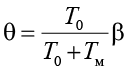 . (6)
. (6)
Учитывая, что для рассматриваемых условий величина τ = 6 месяцев, то в соответствии с графиком [15] значения величины параметра А изменяются от 1,6 до 3,2, а величина приведенной температуры θ – в пределах от 0 до 0,2. Таким образом по данным Рекомендациям [1] возможно рассчитать глубину промерзания грунта в пределах приведенных значений А и θ. Это обстоятельство будет учтено в дальнейших расчетах.
Тм – минимальная среднемесячная температура воздуха за срок наблюдений 10 лет (принимается со знаком плюс) СНиП 23-01-99 [19].
β – поправочный коэффициент за влияние снежного покрова, определяемый по формуле:
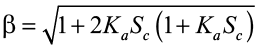 , (7)
, (7)
Т0 – среднегодовая температура грунта по среднемноголетним значениям метеоданных, определяется по формуле:
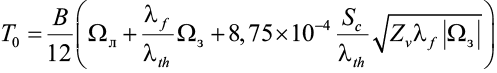 , (8)
, (8)
где В – коэффициент, учитывающий поверхностные условия. Для территорий застройки В = 1; для участков с естественным растительным покровом В = 0,9.
Sc – толщина слоя грунта в м, термическое сопротивление которого равно термическому сопротивлению снежного покрова:
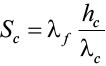 , (9)
, (9)
hc – средняя за зиму толщина снежного покрова в м;
λс – коэффициент теплопроводности снежного покрова согласно [15] принимается равным: при среднезимней толщине снежного покрова до 0,2 м – 0,25 Вт/мК; при среднезимней толщине снежного покрова до 0,4 м – 0,35 Вт/мК.
λf – коэффициент теплопроводности грунта в мерзлом состоянии, ккал/м×ч×град, определяется по [13];
Для данных условий Sc будет равна:
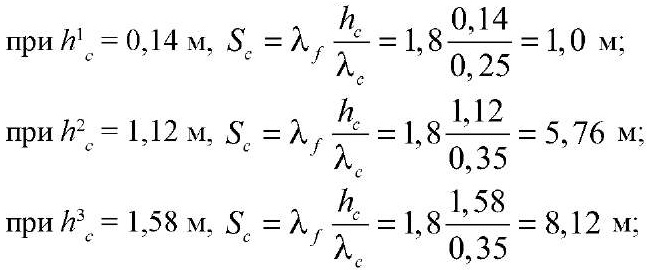
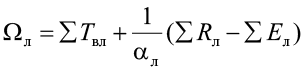 , (10)
, (10)
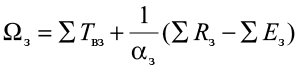 , (11)
, (11)
∑ Tвл и ∑ Твз – суммы среднемесячных температур воздуха соответственно за летний и зимний периоды, °С;
∑ Rл и ∑ Rз – суммы среднемесячных значений радиационного баланса соответственно за летний и зимний периоды, Вт/м²;
∑ Eл и ∑ Eз – суммы среднемесячных значений затрат тепла на испарение соответственно за летний и зимний периоды, Вт/м²;
αл и αз – коэффициенты конвективного теплообмена для летнего и зимнего периодов, Вт/м²К, определяются по формуле:
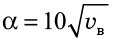 , (12)
, (12)
где υв – средняя скорость ветра, м/сек.
Для летнего периода со средней скоростью ветра, принятой по СНиП II-А. 6-72 «Строительная климатология и геофизика» [20, табл. 7], и равной 3,5 м/сек, αл составит:
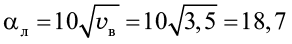 ;
;
для зимнего периода со средней скоростью ветра, равной 5,7 м/сек, αз составит:
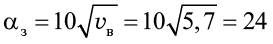 .
.
Среднемесячные значения радиационного баланса и затрат тепла на испарение вычисляются по формулам:
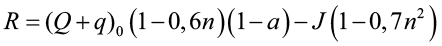 , (13)
, (13)
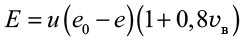 , (14)
, (14)
где
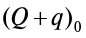 – суммарная солнечная радиация на уровне моря, Вт/м², определялась по [15, табл. 7];
– суммарная солнечная радиация на уровне моря, Вт/м², определялась по [15, табл. 7];
J – эффективное излучение при безоблачном небе, Вт/м², определяется по [15, табл. 5];
а – альбедо поверхности в долях единицы, определяется по [15, табл. 5];
n – наблюдаемая облачность в долях единицы, принимается по метеоданным для района застройки, в расчетах условно принята равной 0,5;
е0 – максимальная упругость водяных паров, гПа, определяется по [15, табл. 6] в зависимости от средней температуры воздуха;
е – наблюдённая абсолютная влажность воздуха, гПа, определяется по [20, табл. 4];
и – коэффициент интенсивности испарения, для территории застройки и = 1.
1.1.3. Результаты расчета
В соответствии с формулой (4) определяем значение параметра Ка по формуле (5):
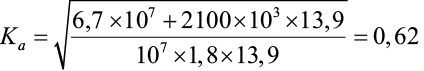 .
.
Для определения параметра А рассчитываем приведенную температуру θ по формуле (6). Для этого рассчитываем величины β по формуле (7) и Т0 по формуле (8).
При отсутствии снежного покрова – β0 = 1.
Среднемесячные значения радиационного баланса и затрат тепла на испарение вычисляются по формулам (13) и (14) для каждого месяца года:
За январь:
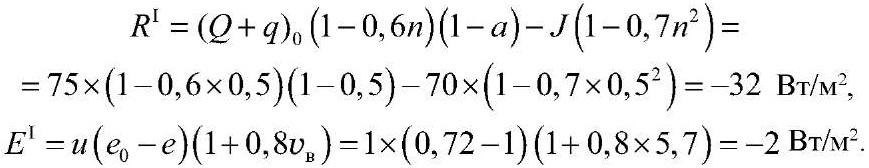
За февраль:
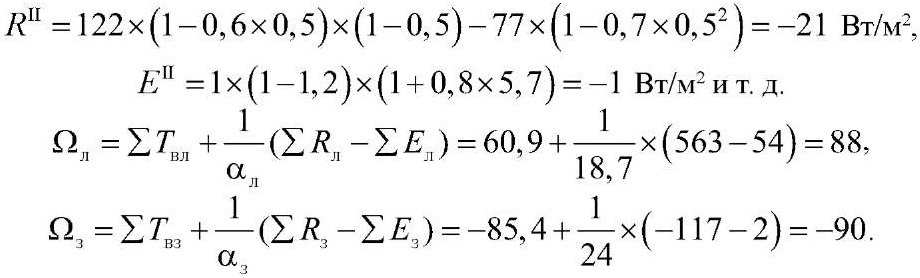
При отсутствии снежного покрова (S0c = 0) Т00 составит:
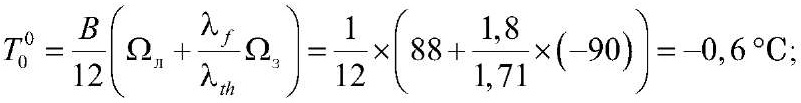
при толщине снежного покрова h1c = 0,14 м – S1c = 1,0 м
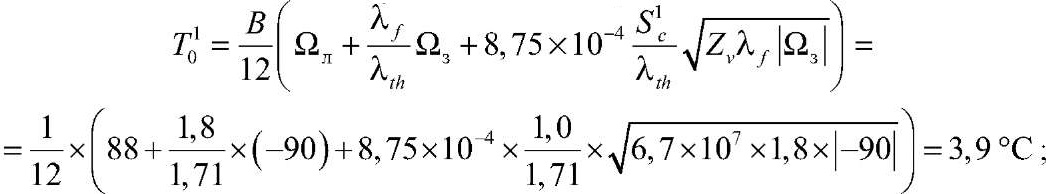
при h2c = 1,12 м – S2c = 5,76 м
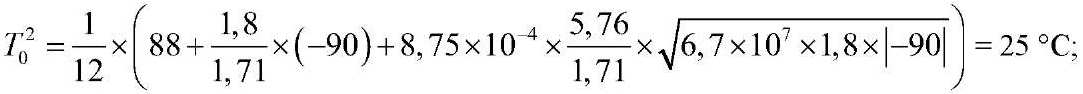
при h3c = 1,58 м – S2c = 8,12 м
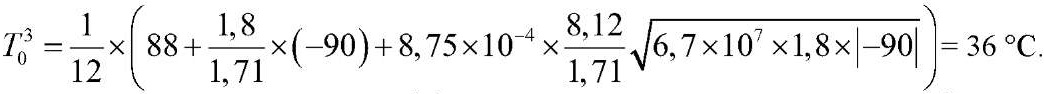
Определение поправочного коэффициента влияния снежного покрова – β
При отсутствии снежного покрова β0 = 1.
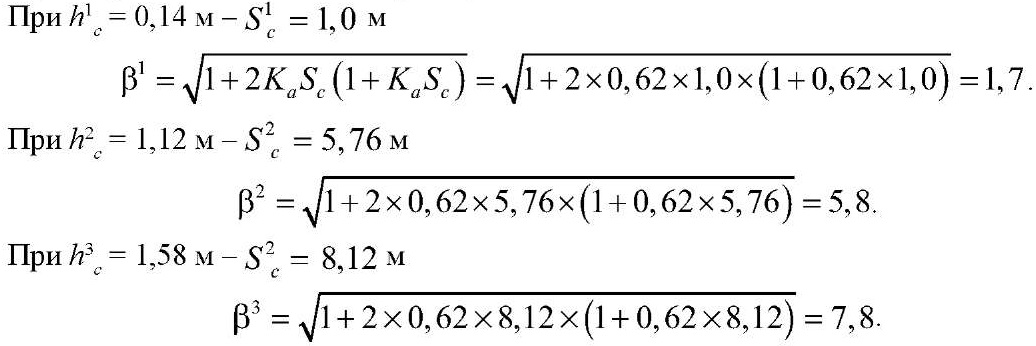
Определение приведенной температуры θ
При отсутствии снежного покрова

Определение коэффициента А по рис. 6 [15] в зависимости от приведенных температур θ при значении τ = 6 мес.
А0 = 3,1; А1 = 1,6;
А2 и А3 – значения выходят за область графика, определение параметра А согласно [15] невозможно.
Глубина сезонного промерзания грунта, Нм, составит:
при отсутствии снежного покрова
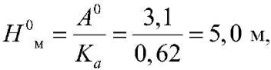
при толщине снежного покрова h1c = 0,14 м
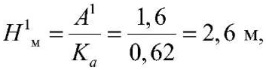
при толщине снежного покрова h2c = 1,12 м и h3c = 1,58 м по [15] глубину промерзания грунта определить невозможно.
1.2. Расчет глубины сезонного промерзания грунтов на пикетах ПК1185 и 1202+50
1.2.1. Исходные данные
На данном пикете ПК1185 и 1202+50 с поверхности и до глубины залегают суглинки мягкопластичные, имеющие следующие физические характеристики: W = 0,274; Wl = 0,333; Wp = 0,212; Ip = 12,1; Il = 0,51; ρ = 1,85 г/см³; ρd = 1,42 г/см³; ρs = 2,68 г/см³; e = 0,874; Sr = 0,91.
Суммарная влажность суглинка составит Wtot = Wр = 0,212.
Тогда при Wtot = 0,212 и ρd = 1,42 г/см³ коэффициенты тепловодности и объемной теплоемкости равны:
для мерзлого грунта: λf = 1,30 Вт/м °С = 1,11 ккал/мч °С; Cf = 1930 кДж/м³ °С = 460 ккал/м³ °С;
для талого грунта: λth= 1,15 Вт/м °С = 1,00 ккал/мч °С; Cth = 2550 кДж/м³ °С = 607 ккал/м³ °С.
Температуру грунта можно определить следующим образом:
Т = 0,4Тсз = 0,4 × (–13,9) = –5,56 °С, по [13] Кн для суглинков равен 0,44
Ww = КнWp = 0,44 × 0,212 = 0,093.
Величина удельной теплоты замерзания воды (таяния льда) в единице объема грунта составит:
Zv = Z0(Wtot – Ww)ρd = 3,35 × 10 4 × (0,212 – 0,093) × 14 200 = 5,7 × 10 7 Дж/м³.
Для данных условий Sc будет равно:
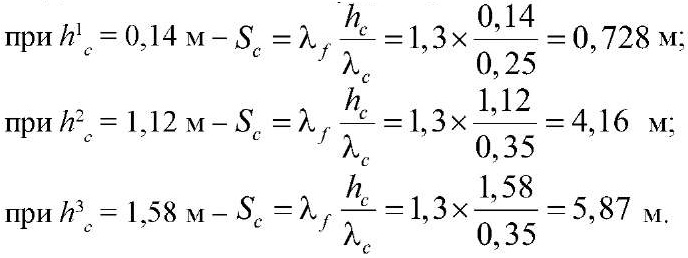
Среднемесячные значения радиационного баланса, затрат тепла на испарение и коэффициенты конвективного теплообмена зависят только от климатических условий площадки строительства и не зависят от свойств грунта, поэтому рассчитанные значения этих величин для пикетов ПК1181 и 1190 характерны и для ПК1185 и 1202+50.
Расчет температуры грунта на поверхности с учетом снежного покрова
Для условий застройки снежный покров не учитывается.
При отсутствии снежного покрова (S0c = 0) Т00 составит:
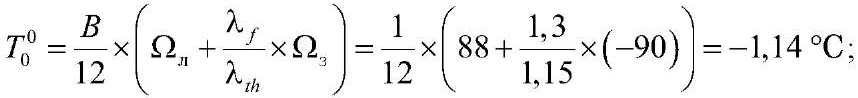
при толщине снежного покрова h1c = 0,14 м – S1c = 0,73 м
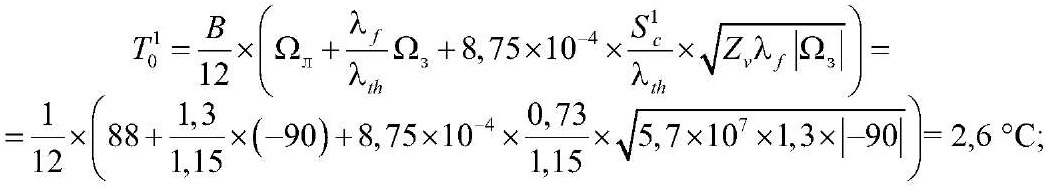
при толщине снежного покрова h2c = 1,12 м – S2c = 4,16 м
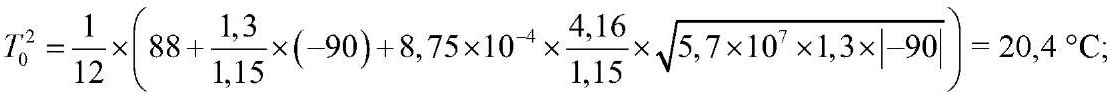
при толщине снежного покрова h3c = 1,58 м – S3c = 5,87 м
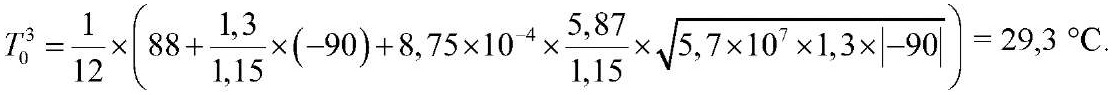
Определяем параметр Ка по формуле (5):
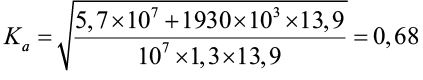 ;
;
Определение поправочного коэффициента влияния снежного покрова – β
При отсутствии снежного покрова β0 = 1.
При толщине снежного покрова h1c = 0,14 м – S1c = 0,73 м
 ;
;
при толщине снежного покрова h2c = 1,12 м – S2c = 4,16 м
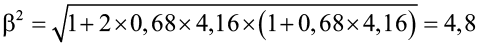 ;
;
при толщине снежного покрова h3c = 1,58 м – S3c = 5,87 м
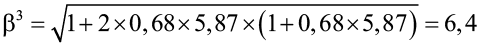 .
.
Определение приведенной температуры θ
При отсутствии снежного покрова
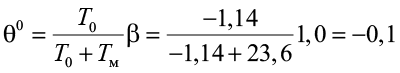 ;
;
при толщине снежного покрова h1c = 0,14 м
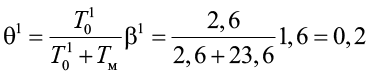 ;
;
при толщине снежного покрова h2c = 1,12 м
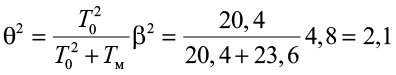 ;
;
при толщине снежного покрова h3c = 1,58 м
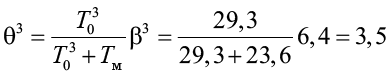 .
.
Определение коэффициента А по рис. 6 [15] в зависимости от приведенных температур θ при значении τ = 6 мес.
А0 = 3,3; А1 = 1,6;
А2 и А3 – значения выходят за область графика, определение параметра А согласно [15] невозможно.
Глубина сезонного промерзания грунта, Нм, составит:
при отсутствии снежного покрова
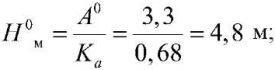
при толщине снежного покрова h1c = 0,14 м
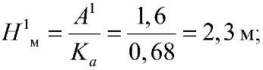
при толщине снежного покрова h2c = 1,12 м и h3c = 1,58 м по [15] глубину промерзания грунта определить невозможно.
2. Расчет глубины сезонного промерзания грунтов по «Справочнику по строительству на вечномерзлых грунтах» [16]
2.1. Расчет глубины сезонного промерзания грунтов на пикетах ПК1181 и 1190
Нормативная глубина сезонного промерзания грунта, dfn, м, в соответствии с [16] определяется по формуле:
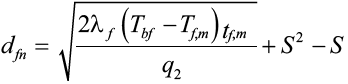 , (15)
, (15)
где
q2 = Lν – 0,5Cf(Tf,m – Tbf), (16)
здесь Lν – теплота замерзания грунта, Дж/м³ (ккал/м³), определяемая по [13] при температуре грунта T = 0,5(Tf,m – Tbf), °С, см. формулу (1);
Tf,m, tf,m – соответственно средняя по многолетним данным температура воздуха за период отрицательных температур (равна –13,9 °С) и продолжительность этого периода (4392 ч), принимаемые по [19];
Tbf – температура начала замерзания грунта, °С, определяемая по [13], для супеси равна 0,1 °С;
S – толщина слоя грунта, термическое сопротивление которого равно термическому сопротивлению снега, определяется по формуле (9);
wtot – суммарная влажность грунта, принимается равной естественной влажности грунта, равной 0,34;
λс – коэффициент теплопроводности снежного покрова, принимается равным 0,25 ккал/мч °С.
q2 = z0(wtot – ww)ñd – 0,5Cf(Tf,m – Tbf) = 80 000 × (0,34 – 0,065) × 1,2 – 0,5 × 500 × (13,9 – 0,1) = 29 850 ккал/м³.
Глубина сезонного промерзания грунта, dfn, составит:
при отсутствии снежного покрова:
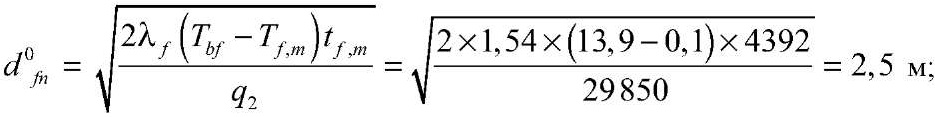
при толщине снежного покрова h1c = 0,14 м
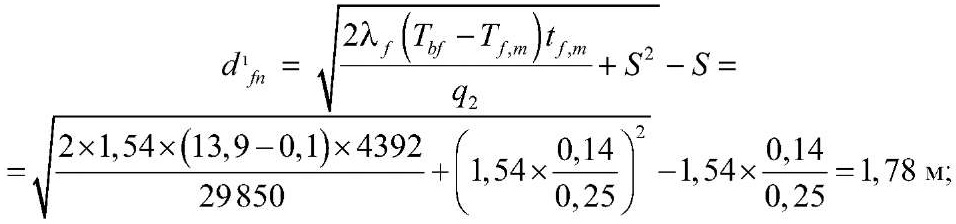
при h2c = 1,12 м
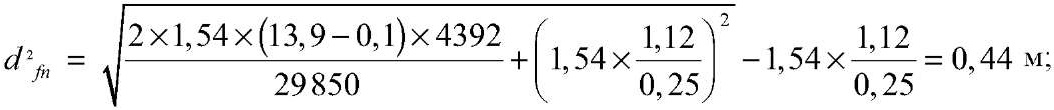
при h3c = 1,58 м
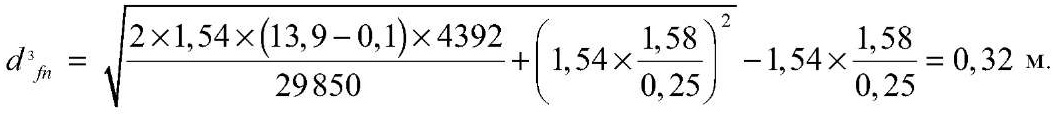
2.2. Расчет глубины сезонного промерзания грунтов на пикетах ПК1185 и 1202+50
При значении q2, равном
q2 = z0(wtot – ww)ñd – 0,5Cf(Tf,m – Tbf) = 80 000 × (0,274 – 0,093) × 1,42 – 0,5 × 460 × (13,9 – 0,1) = 23 735,6 ккал/м³,
глубина сезонного промерзания грунта, df,n, составит:
при отсутствии снежного покрова
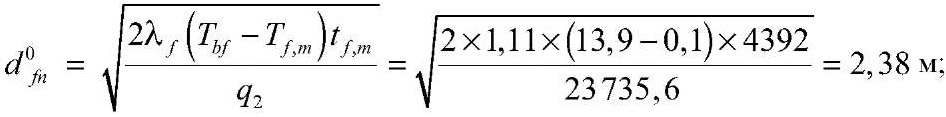
при h1c = 0,14 м
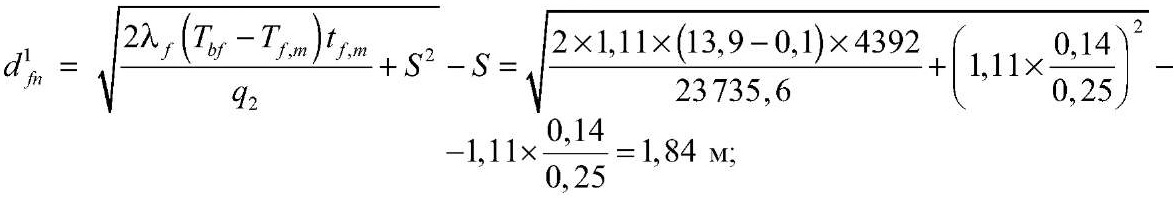
при h2c = 1,12 м
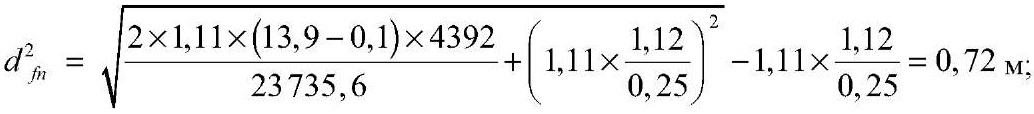
при h3c = 1,58 м
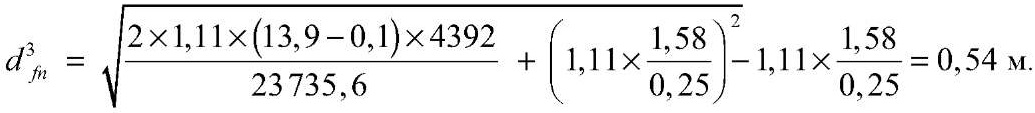
3. Расчет глубины сезонного промерзания грунтов по «Рекомендациям по учету и предупреждению деформаций и сил морозного пучения грунтов» [17]
3.1. Расчет глубины сезонного промерзания грунтов на пикетах ПК1181 и 1190
Значение нормативной глубины сезонного промерзания грунта определяем расчетным путем по [14]:
 , (17)
, (17)
где d0 – величина, равная для супесей 0,28 м;
Мt – безразмерный коэффициент, численно равный сумме абсолютных значений среднемесячных отрицательных температур за зиму в данном районе, принимаемых по [19].
Данные о температуре воздуха приняты по близлежащему району – п. Кировское.
Среднемесячные отрицательные температуры воздуха (Тм, °С) в зимний период по многолетним данным представлены в табл. 1.
Таблица 1
Температуры приземного воздуха для п. Кировское
Table 1
Surface air temperatures for the Kirovskoye settlement
|
Температура приземного воздуха, °С |
||||||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
Средняя |
|
-23,6 |
-19,7 |
-12 |
-1,7 |
5,6 |
11,7 |
15,6 |
15,5 |
10,4 |
2,1 |
-9,1 |
-19,3 |
-2,04 |
Расчетная среднемесячная температура воздуха при продолжительности зимнего периода τ = 183 будет равна Т0 ≈ –13,9 °С.
Нормативная глубина сезонного промерзания глинистого грунта по [14] равна:
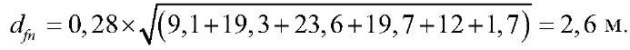
Расчетная глубина сезонного промерзания грунта, df , м, равна:
df = kh × dfn , (18)
где kh – коэффициент, учитывающий влияние теплового режима сооружения, принимаемый равным 1,0 по [14].
Определение глубины промерзания грунта под слоем снега
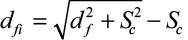 , (19)
, (19)
где sc – толщина эквивалентного слоя грунта, находится по формуле:
 , (20)
, (20)
λf – теплопроводность мерзлого грунта, равна 1,80 Вт/м °С;
αc – коэффициент теплоотдачи свободной поверхности, равен 23 Вт/м °С;
δс – толщина снега, м;
λс – теплопроводность снега, составляет 0,25 Вт/м °С.
Глубина сезонного промерзания грунта, dfn, составит:
при толщине снежного покрова h1c = 0,14 м
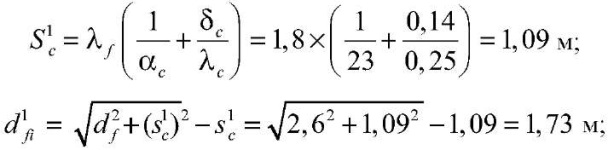
при h2c = 1,12 м
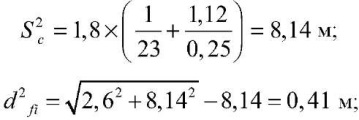
при h3c = 1,58 м
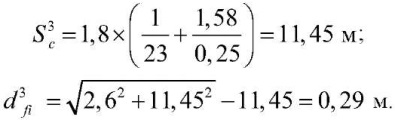
3.2. Расчет глубины сезонного промерзания грунтов на пикетах ПК1185 и 1202+50
Нормативная глубина сезонного промерзания глинистого грунта по [14] равна:

Глубина сезонного промерзания грунта, dfn, составит:
при h1c = 0,14 м
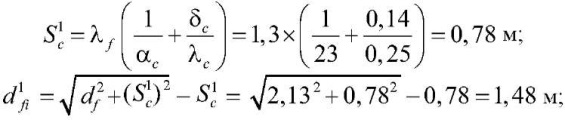
при h2c = 1,12 м
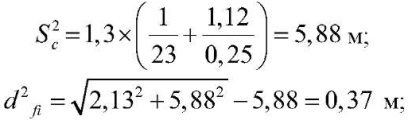
при h3c = 1,58 м
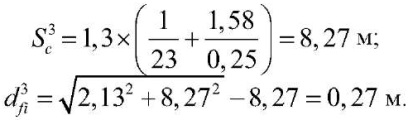
4. Расчет глубины сезонного промерзания грунтов по «Рекомендациям по прогнозу теплового состояния мерзлых грунтов» [18]
4.1. Расчет глубины сезонного промерзания грунтов на пикетах ПК1181 и 1190
Нормативная глубина сезонного промерзания грунта, dfn, м, определяется в соответствии с [18] по формуле:
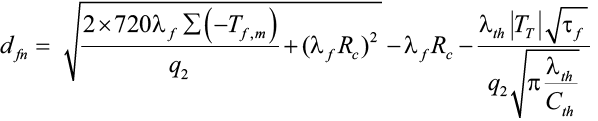 , (21)
, (21)
где q2, Tbf , λf, λc – те же обозначения, что и в расчете 2;
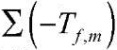 – сумма среднемесячных температур за период промерзания, принимается по [19] и составляет -85,4;
– сумма среднемесячных температур за период промерзания, принимается по [19] и составляет -85,4;
λth – коэффициент тепловодности талого грунта, для супеси λth = 1,71 Вт/мК = 1,48 ккал/мч °С;
Cth – объемная теплоемкость талого грунта, для супеси Cth = 2945 кДж/м³К = 701 ккал/м³ °С;
τf – продолжительность периода промерзания, для данных климатических условий принимается по [19] и составляет 4392 ч;
Rs – термическое сопротивление снега при промерзании, принимается по [18, рис. 8] в зависимости от толщины снежного покрова;
ТТ – среднеинтегральное значение температуры в талой зоне при промерзании, определяется по [18] в зависимости от температуры грунта tгр, определяемой по [18, рис. 2] в зависимости от термического сопротивления теплоизоляции и сумм температур за летний 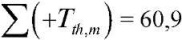 и зимний
и зимний 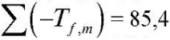 периода.
периода.
При толщине снежного покрова h1c = 0,14 м и термическом сопротивлении теплоизоляции R1s = 0,4 при λth = λf температура грунта по [18, рис. 2] tгр = –2 °С. Понижение среднегодовой температуры грунта для соотношения λf /λth = 1,04 в соответствии с [18, рис. 3] будет равно –0,4 °С. Таким образом, истинное значение среднегодовой температуры грунта будет равно: tгр= –2 + (–0,4) = –2,4 °С. ТТ по [18] равен Т1Т = 5,4 °С.
При толщине снежного покрова h2c = 1,12 м и термическом сопротивлении теплоизоляции R2s = 2,1 при λth= λf температура грунта по [18, рис. 2] tгр = –2,5 °С. Понижение среднегодовой температуры грунта для соотношения λf /λth = 1,04 в соответствии с [18, рис. 3] будет равно –0,4 °С. Таким образом, истинное значение среднегодовой температуры грунта будет равно: tгр = –2,5 + ( –0,4) = –2,9 °С, Т2Т = 7 °С.
При толщине снежного покрова h3c = 1,58 м и термическом сопротивлении теплоизоляции R3s = 3,5 при λth = λf температура грунта по [18, рис. 2] tгр = 1 °С. Понижение среднегодовой температуры грунта для соотношения λf /λth = 1,04 в соответствии с [18, рис. 3] будет равно –0,4 °С. Таким образом, истинное значение среднегодовой температуры грунта будет равно: tгр = 0,4 + (–0,4) = 0 °С, Т2Т = 1 °С.
Глубина сезонного промерзания грунта, dfn, составит:
при отсутствии снежного покрова;
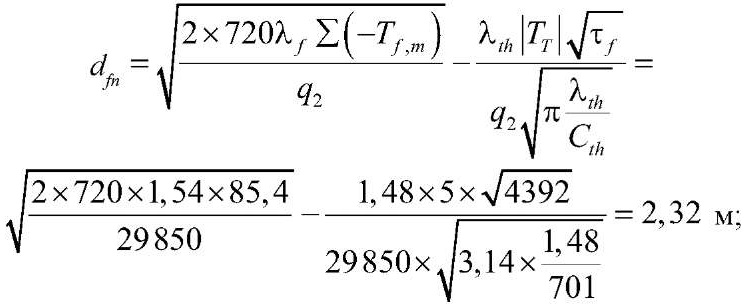
при h1c = 0,14 м
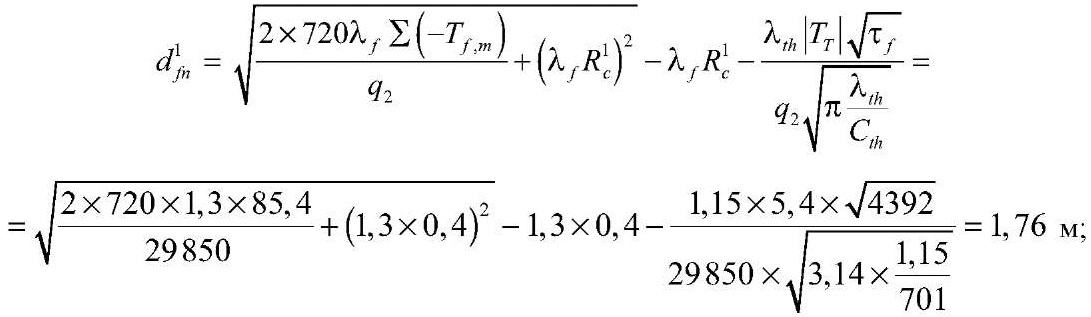
при h2c = 1,12 м
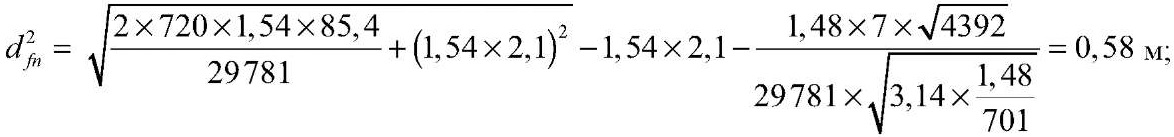
при h3c = 1,58 м
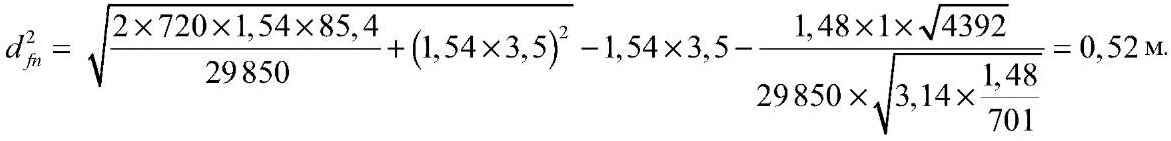
4.2. Расчет глубины сезонного промерзания грунтов на пикетах ПК1185 и 1202+50
Глубина сезонного промерзания грунта, dfn, составит:
при отсутствии снежного покрова
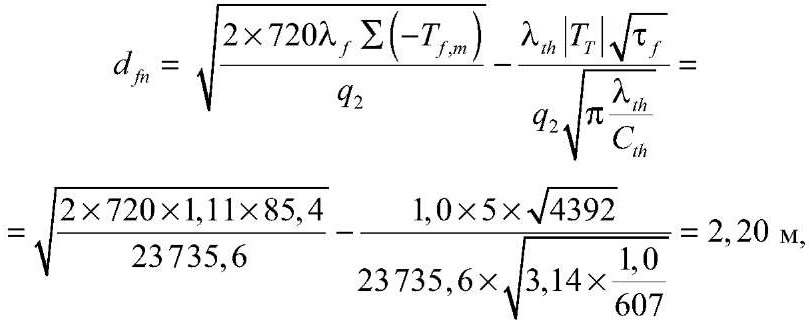
при h1c = 0,14 м
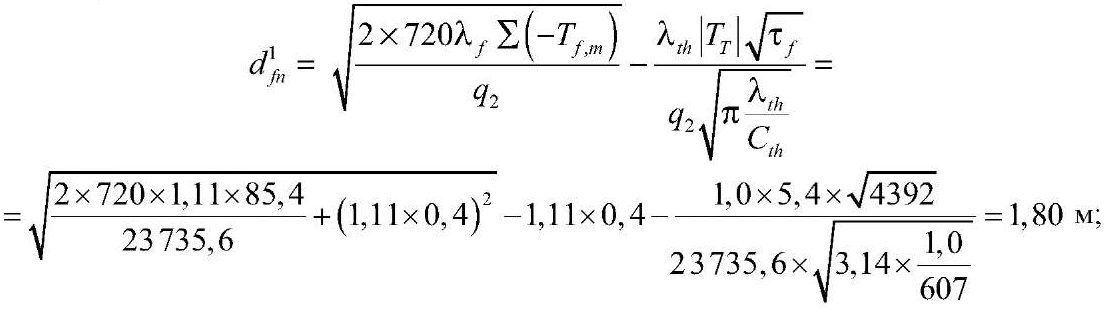
при h2c = 1,12 м
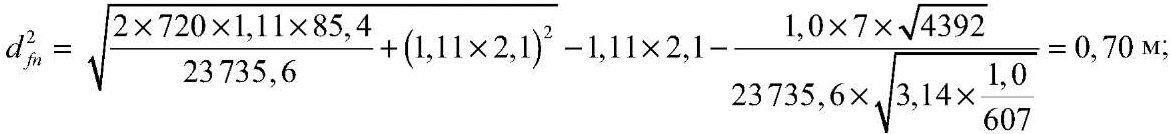
при h3c = 1,58 м
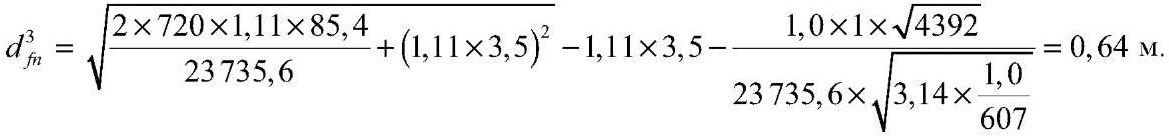
Результаты расчетов по четырем инженерным методикам сведены в табл. 2.
Таблица 2
Максимальная глубина промерзания, определенная инженерными методами
Table 2
Maximum freezingt depth determined by engineering methods
|
Тип грунта |
Высота снежного покрова, м |
Глубина промерзания, м |
|||
|
ИМ1 |
ИМ2 |
ИМ3 |
ИМ4 |
||
|
Супесь ПК1181 и 1190 |
0 |
5,0 |
2,50 |
2,60 |
2,32 |
|
0,14 |
2,6 |
1,78 |
1,73 |
1,76 |
|
|
1,12 |
– |
0,44 |
0,41 |
0,58 |
|
|
1,58 |
– |
0,32 |
0,29 |
0,52 |
|
|
Суглинок ПК1185 и 1202+50 |
0 |
4,8 |
2,38 |
2,13 |
2,20 |
|
0,14 |
2,3 |
1,84 |
1,48 |
1,80 |
|
|
1,12 |
– |
0,72 |
0,37 |
0,70 |
|
|
1,58 |
– |
0,54 |
0,27 |
0,64 |
|
5. Расчет глубины сезонного промерзания грунтов в программных комплексах Борей 3D и Frost 3D
Теплотехнические расчеты выполнялись в программных комплексах Борей 3D и Frost 3D, предназначенных для расчета динамики изменений температурного поля грунтов оснований зданий и сооружений с учетом теплового влияния инженерных сооружений. Программные комплексы реализуют математический аппарат моделирования распространения температурных полей в среде с фазовыми переходами и соответствуют требованиям [13].
Процесс распространения тепла в грунте с фазовыми переходами в спектре отрицательных температур описывается дифференциальным уравнением, записанным в энтальпийной форме:
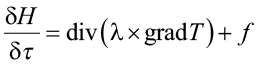 , (22)
, (22)
где
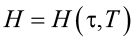 – энтальпия (теплосодержание), отнесенная к единице объема грунта;
– энтальпия (теплосодержание), отнесенная к единице объема грунта;
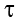 – время;
– время;
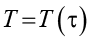 – температура грунта;
– температура грунта;
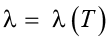 – коэффициент теплопроводности грунта;
– коэффициент теплопроводности грунта;
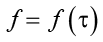 – мощность внутренних источников тепла.
– мощность внутренних источников тепла.
Энтальпия является функцией температуры от времени и координат. С учетом теплоты фазовых переходов в грунте энтальпия описывается уравнением (2):
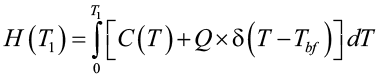 , (23)
, (23)
где C = C = (T)– теплоемкость грунта;
Q – теплота фазового перехода;
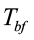 – температура фазового перехода;
– температура фазового перехода;
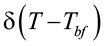 – дельта-функция.
– дельта-функция.
В программах реализованы два конечно-разностных метода для решения исходного дифференциального уравнения:
– метод явной двухслойной разностной схемы;
– метод с динамическим разбиением области на подобласти с явной и неявной вычислительной схемой. В качестве неявной вычислительной схемы применен метод простой итерации. Для улучшения сходимости неявного метода применяется метод регуляризации и динамический подбор шага по времени.
Исходные данные для выполнения расчетов
В качестве исходных данных использовались следующие параметры:
– климатические условия для задания верхнего граничного условия (ГУ) модели (среднемесячная температура воздуха, скорость ветра, высота и теплопроводность снежного покрова);
– физические и теплофизические характеристики грунтов (влажность, плотность, температура фазового перехода, теплоемкость и теплопроводность в талом и мерзлом состояниях);
– начальное температурное распределение в грунтовом массиве.
На верхнем климатическом ГУ приняты значения среднемесячных температур приземного воздуха, соответствующие данным [19]. Среднемесячные значения температур воздуха приняты по ближайшей метеорологической станции, расположенной в п. Кировское, и приведены в табл. 1.
Среднемесячные значения скорости ветра и высоты снежного покрова приняты в соответствии с архивными данными и приведены в табл. 3.
Значения необходимых в качестве исходных данных физических и теплофизических свойств грунтов приведены в табл. 4 и 5.
Таблица 3
Скорость ветра и высота снежного покрова
Table 3
Wind speed and snow cover height
|
Наименование параметра |
Среднее значение по месяцам (годовое) |
||||||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
Год |
|
|
Скорость ветра, м/с |
2,9 |
2,8 |
3,0 |
2,9 |
2,7 |
2,4 |
2,2 |
2,4 |
2,9 |
3,4 |
3,3 |
3,2 |
2,8 |
Таблица 4
Физические и теплофизические свойства грунтов
Table 4
Physical and thermophysical properties of soils
|
Наименование грунта |
Wtot, % |
ρd, г/см³ |
Tbf, °C |
λth, Вт/(м °С) |
λf, Вт/(м °С) |
Cth, |
Cf, |
|
Супесь |
0,22 |
1,51 |
-1,16 |
1,31 |
1,47 |
2,78 |
2,10 |
|
Суглинок |
0,28 |
1,37 |
-0,43 |
1,41 |
1,57 |
2,93 |
2,15 |
Таблица 5
Зависимость влажности за счет незамерзшей воды от температуры
Table 5
Dependence of moisture content due to unfrozen water on temperature
|
Влажности за счет незамерзшей воды, Ww, д. е. |
|||||||||||
|
Температура |
-0,1 |
-0,4 |
-0,6 |
-1,1 |
-2,1 |
-3,1 |
-4,1 |
-6,1 |
-8,1 |
-10,1 |
-15,1 |
|
Супесь |
0,16 |
0,13 |
0,12 |
0,10 |
0,08 |
0,08 |
0,07 |
0,07 |
0,07 |
0,06 |
0,06 |
|
Суглинок |
0,17 |
0,15 |
0,14 |
0,13 |
0,11 |
0,10 |
0,10 |
0,09 |
0,09 |
0,09 |
0,08 |
Создание модели и приведение ее в стационарный режим
В качестве расчетной области принят трехмерный грунтовый массив глубиной 50 м, с размерами в плане 1,0 × 1,0 м. Шаг сетки принят адаптивным от 0,1 × 0,1 × 0,1 м до 1,0 × 1,0 × 3,0 м.
Прогнозные расчеты выполнялись на период 50 лет до 2071 года. Интервал выдачи результатов – 1 месяц. Изменяемым параметром в расчетах принята температура приземного воздуха, задаваемая в соответствии с трендом. Остальные параметры климатических условий, а также граничные условия приняты постоянными на весь период расчета.
В табл. 6 приведены ГУ модели.
Таблица 6
Граничные условия модели
Table 6
Boundary conditions of the model
|
Локация распространения ГУ |
Характеристика ГУ |
Месяц |
|||||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
||
|
При отсутствии снега |
Температура, °С |
-23,6 |
-19,7 |
-12 |
-1,7 |
5,6 |
11,7 |
15,6 |
15,5 |
10,4 |
2,1 |
-9,1 |
-19,3 |
|
Коэффициент теплообмена, Вт/м²×К |
18,4 |
17,9 |
18,7 |
18,2 |
17,6 |
16,0 |
15,3 |
16,3 |
18,1 |
20,2 |
19,9 |
19,4 |
|
|
При средней высоте снега 0,14 м |
Температура, °С |
-23,6 |
-19,7 |
-12 |
-1,7 |
5,6 |
11,7 |
15,6 |
15,5 |
10,4 |
2,1 |
-9,1 |
-19,3 |
|
Коэффициент теплообмена, Вт/м²×К |
0,99 |
0,98 |
1,10 |
2,25 |
12,9 |
16,0 |
15,3 |
16,3 |
17,3 |
12,5 |
2,65 |
1,20 |
|
|
При средней высоте снега 0,23 м |
Температура, °С |
-23,6 |
-19,7 |
-12 |
-1,7 |
5,6 |
11,7 |
15,6 |
15,5 |
10,4 |
2,1 |
-9,1 |
-19,3 |
|
Коэффициент теплообмена, Вт/м²×К |
0,62 |
0,61 |
0,69 |
1,45 |
10,8 |
16,0 |
15,3 |
16,3 |
18,1 |
9,89 |
1,70 |
0,75 |
|
|
При средней высоте снега 1,12 м |
Температура, °С |
-23,6 |
-19,7 |
-12 |
-1,7 |
5,6 |
11,7 |
15,6 |
15,5 |
10,4 |
2,1 |
-9,1 |
-19,3 |
|
Коэффициент теплообмена, Вт/м²×К |
0,13 |
0,13 |
0,15 |
0,32 |
4,53 |
16,0 |
15,3 |
16,3 |
13,2 |
3,41 |
0,38 |
0,16 |
|
|
При средней высоте снега 1,58 м |
Температура, °С |
-23,6 |
-19,7 |
-12 |
-1,7 |
5,6 |
11,7 |
15,6 |
15,5 |
10,4 |
2,1 |
-9,1 |
-19,3 |
|
Коэффициент теплообмена, Вт/м²×К |
0,09 |
0,09 |
0,10 |
0,23 |
3,47 |
16,0 |
15,3 |
16,3 |
11,8 |
2,54 |
0,27 |
0,11 |
|
|
Боковые и нижняя грани расчетной области |
Тепловой поток, |
0,0 |
|||||||||||
Перед началом теплотехнических расчетов модель приводилась в естественное температурное состояние, когда без влияния изменения высоты снежного покрова ГУ климата обеспечивают неизменяемость температурного состояния модели во времени.
По результатам приведения модели в стационарный режим по климатическим данным [19] и данным архивов получены начальные графики распределения температур по глубине на начало летнего периода для супеси и суглинка, которые приведены на рис. 1 и 2 соответственно.
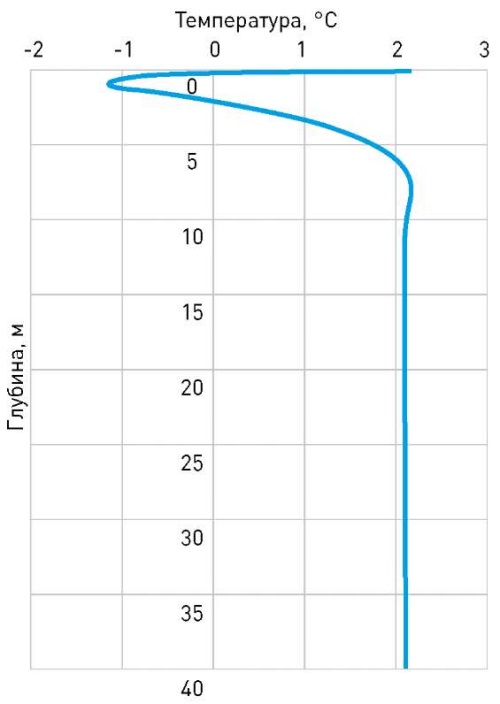
Рис. 1. График распределения температур по глубине для супеси
Fig. 1. Temperature distribution by depth for sandy loam
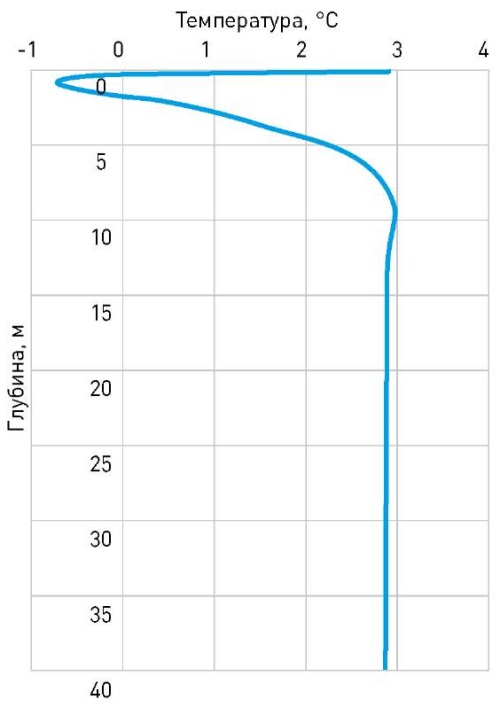
Рис. 2. График распределения температур по глубине для суглинка
Fig. 2. Temperature distribution by depth for loam
Результаты расчетов
Значения максимальной глубины промерзания при расчетах с различной высотой снежного покрова и в различных программных комплексах представлены в сводной табл. 7.
Таблица 7
Максимальная глубина промерзания, определенная численными методами
Table 7
Maximum freezing depth determined by numerical methods
|
Тип грунта |
Высота снежного покрова, м |
Глубина промерзания, м |
|
|
Борей 3D |
Frost 3D |
||
|
Супесь ПК1181 и 1190 |
0 |
3,29 |
3,41 |
|
0,14 |
2,09 |
2,28 |
|
|
0,23 |
1,56 |
1,54 |
|
|
1,12 |
– |
0,04 |
|
|
1,58 |
– |
– |
|
|
Суглинок ПК1185 и 1202+50 |
0 |
3,30 |
3,31 |
|
0,14 |
2,35 |
2,49 |
|
|
0,23 |
1,91 |
1,88 |
|
|
1,12 |
0,34 |
0,39 |
|
|
1,58 |
– |
0,06 |
|
Анализ результатов проведенных расчетов показал отличие искомых величин, полученных по различным источникам друг от друга, кроме того, выявлены недостатки и трудности, с которыми может столкнуться проектировщик при расчете глубин промерзания грунтов. Расчет глубины промерзания грунта с учетом снежного покрова по «Рекомендациям по теплотехническим расчетам и прокладке трубопроводов в районах с глубоким сезонным промерзанием грунтов» [15] основан на методике, разработанной Г.В. Порхаевым. Расчет по этим рекомендациям с определением всех составляющих теплового баланса поверхности грунта – метеорологических, радиационных, тепловых и физических свойств снега и грунта в талом и мерзлом состояниях – представляет значительные сложности и может быть выполнен лишь с той или иной степенью приближения, что осложняет применение рекомендаций на практике, особенно если учесть, что для достоверности получаемых результатов необходимо пользоваться средними многолетними данными. Кроме того, проведенные расчеты по этим рекомендациям (табл. 2, рис. 3, 4) показали, что полученная величина глубины промерзания несколько завышена и определить глубину промерзания грунта при толщине снежного покрова большего 0,15 м (для данных условий) не представляется возможным из-за невозможности определения параметра А по графику для больших слоев снега.
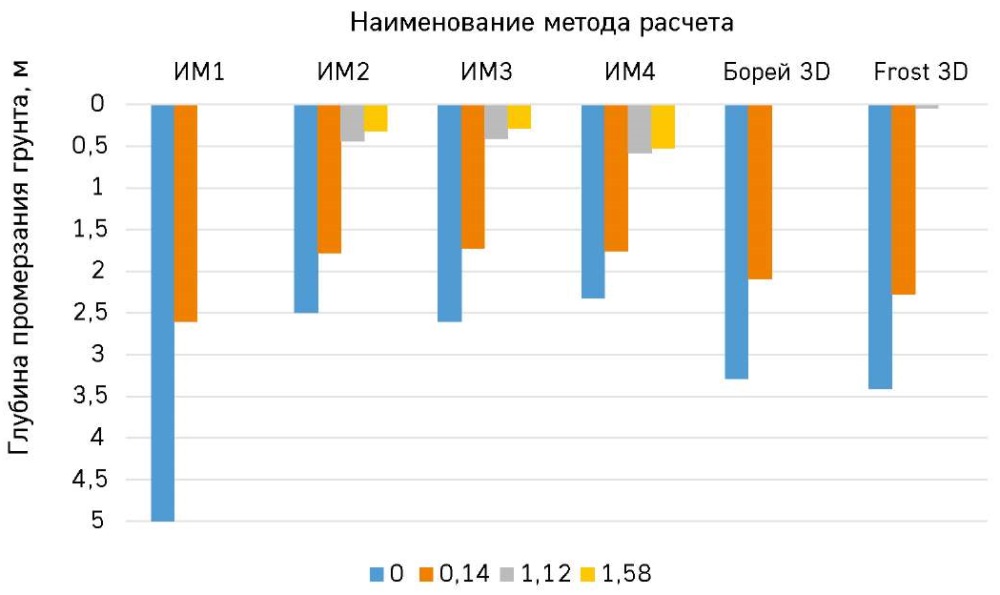
Рис. 3. Расчетные значения глубины промерзания для ПК1181 и 1190, определенные инженерными (ИМ1–ИМ4) и численными (Борей 3D и Frost 3D) методами
Fig. 3. Calculated values of freezing depth for PK 1181 and PK 1190 determined by engineering methods (EM1–EM4) and numerical methods (Borey 3D and Frost 3D)
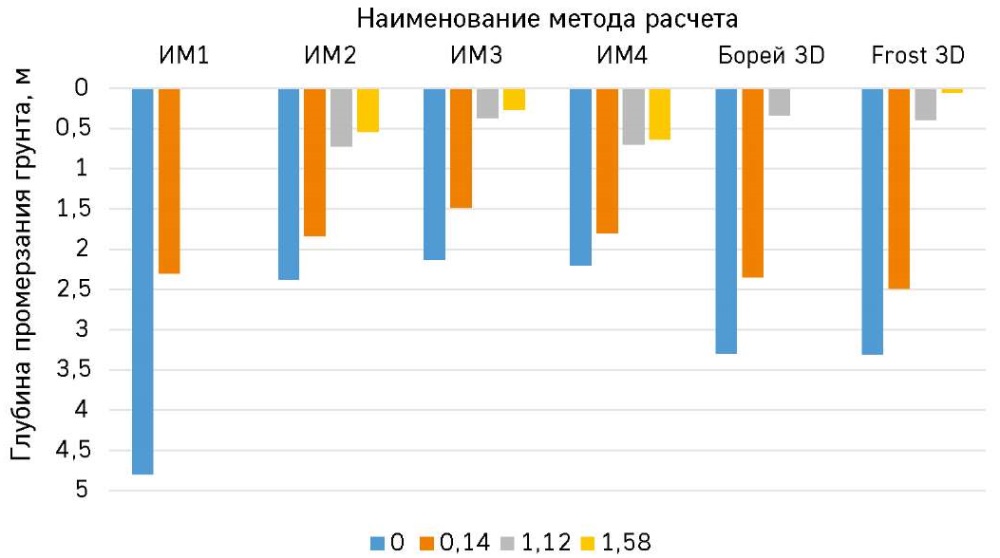
Рис. 4. Расчетные значения глубины промерзания песка, определенные инженерными (ИМ1–ИМ4) и численными (Борей 3D и Frost 3D) методами
Fig. 4. Calculated values of sand freezing depth determined by engineering methods (EM1–EM4) and numerical methods (Borey 3D and Frost 3D)
В основу расчетов глубины промерзания грунта в [16][18] заложена формула Стефана. Различие в методиках заключается в том, что в [18] учитывается влияние талого грунта на глубины промерзания, несколько снижая ее, при этом существенно усложняется расчет, поэтому для упрощения расчетов и некоторого запаса предпочтительнее пользоваться расчетом по [16], кроме того, в [13] используется та же методика, но только без учета теплоизоляции (снежного покрова).
Расчет по методике, изложенной в [17], позволяет приближенно оценить глубину промерзания грунта под слоем снега и может использоваться для ориентировочных расчетов. В основе расчета лежит определение глубины промерзания грунта по [14].
Полученные величины глубин сезонного промерзания грунтов с учетом снежного покрова, рассчитанные по разным методикам, сведены в табл. 2 и представлены на рис. 3 и 4.
Численные расчеты имеют схожие между собой результаты. Наибольшее отличие (4 %) в величине глубины промерзания соответствует оголенной поверхности и заснеженной поверхности мощностью 0,14 м (6–9 %). При значительной высоте снежного покрова 1,12 и 1,58 м также отмечены отличия в величине расчетной глубины промерзания грунта. Программный комплекс Frost 3D определяет глубину промерзания супеси со снегом h = 1,12 м и суглинка с h = 1,58 м, программный комплекс Борей 3D не определяет промерзание грунта при данных условиях.
Инженерные методы ИМ2–ИМ4 дают схожие результаты для оголенной поверхности и снежного покрова высотой 0,14 м, отличаясь друг от друга на 20 %. Большие отличия (в 44 %) характерны для заснеженных площадок (1,12–1,58 м). При этом инженерные расчеты показывают существенно меньшие значения глубины промерзания по сравнению с численными расчетами (32–47 %).
Численные методы базируются на нормативных документах [13] или ИМ3 для данного исследования.
Численные расчеты определили существенно большую глубину промерзания грунта. С одной стороны, это реализует дополнительный запас, с другой – приводит к перерасходу материала (большая длина свай, наличие излишней противопучинистой обмазки и др.).
Для повышения эффективности определения глубины сезонного промерзания грунтов следует выполнить разработку нового метода и модификацию теплотехнических програмных комплексов с выполнением полевых экспериментальных исследований.
Выводы
Выполнены сравнительные расчеты инженерными и численными методами по определению глубины сезонного промерзания грунта на примере двух площадок, расположенных в Сахалинской области.
Расчет глубины промерзания грунта с определением всех составляющих теплового баланса поверхности грунта – метеорологических, радиационных, тепловых и физических свойств снега и грунта в талом и мерзлом состояниях – представляет значительные сложности и может быть выполнен лишь с той или иной степенью приближения, что осложняет применение данной методологии на практике, особенно если учесть, что для достоверности получаемых результатов необходимо пользоваться средними многолетними данными.
Наиболее достоверные результаты расчетов, вошедшие в нормативные документы [13], получены по методикам, в которые заложена формула Стефана с учетом снежного покрова.
Численные расчеты для условий оголенной поверхности дают завышенные значения до 47 % по сравнению с инженерными нормативными расчетами.
Дальнейшее совершенствование как инженерных, так и численных методик расчета сезонной глубины промерзания грунта позволит обеспечить надежность фундаментов и сократить затраты на их устройство. Разработку следует вести с использованием результатов натурных замеров на нескольких типовых площадках.
Список литературы
1. <i>Alekseev A., Gribovskii G., Vinogradova S.</i> Analytical solution of the semi-infinite problem of soil freezing with numerical solutions in various simulation software. IOP Conference Series: Materials Science and Engineering. 2018;365:042059. https://doi.org/10.1088/1757-899x/365/4/042059
2. <i>Кудрявцев С.А.</i> Геотехническое моделирование процесса промерзания и оттаивания сезонно промерзающих морозоопасных грунтов юга Дальнего Востока. В: Современные технологии – железнодорожному транспорту и промышленности. Труды 44-й Всерос. науч.-практ. конф. ученых транспортных вузов, инженерных работников и представителей Академии науки. Том 1. Хабаровск; 2006, с. 40–45.
3. <i>Ким Х.Ч.</i> Совершенствование методов расчета глубины сезонного промерзания пучинистых грунтов земляного полотна железнодорожного пути [диссертация]. Новосибирск; 2013.
4. <i>Ермилов М.В., Болотина Ю.О., Якушев А.А.</i> Факторы неравномерности сезонного промерзания грунтов. В: Строительство – формирование среды жизнедеятельности: сб. материалов XIX Междунар. межвузовской науч.-практ. конф. студентов, магистрантов, аспирантов и молодых ученых. Москва: Национальный исследовательский Московский государственный строительный университет; 2016, с. 1033–1037.
5. <i>Калашников А.В., Деменков О.В.</i> Постановка задачи к расчету глубин сезонного промерзания-оттаивания обводненных грунтов. В: Проблемы освоения нефтегазовых месторождений приарктических территорий России. Материалы Всерос. науч.-практ. конф. Вып. 3. Архангельск: Северный (Арктический) федеральный университет им. М.В. Ломоносова; 2020, с. 32–37.
6. <i>Ершов Э.Д., Нефедьева Ю.А., Мотенко Р.Г., Пармузин С.Ю.</i> Прогноз изменения глубины сезонного оттаивания и промерзания грунтов под влиянием нефтяного загрязнения. Вестник Московского университета. Сер. 4: геология. 2007;(6):7–50.
7. <i>Заболотник С.И., Заболотник П.С.</i> Температура, сезонное протаивание и промерзание грунтов под зданиями якутской ТЭЦ и на прилегающей к ним территории. Наука и образование. 2009;(4):70–75.
8. <i>Каркашадзе Г.Г., Бельченко Е.Л.</i> Определение глубины сезонного промерзания грунтов при наличии многослойного утепления на поверхности. Горный информационно-аналитический бюллетень. 1999;(1):24–26.
9. <i>Li J.</i> Macro-micro characteristics of geopolymer-stabilized saline soil in seasonal frozen soil region. Transoilcold 2023. Материалы 6-го Междунар. симпозиума по строительному инжинирингу грунтовых сооружений на транспорте в холодных регионах. Москва: Дашков и К; 2023, с. 193.
10. <i>Тукбаев Н.Э.</i> Численное моделирование сезонного теплообмена в верхних слоях грунта без промерзания. B: Радиоэлектроника, электротехника и энергетика: тезисы докладов 28-й Междунар. науч.-техн. конф. студентов и аспирантов. Москва; 2022, с. 525.
11. <i>Гудун М.А.</i> Методика расчета сезонного промерзания деятельного слоя грунта. Динамика систем, механизмов и машин. 2014;(2):75–79.
12. <i>Иванов К.С., Галлямов Д.Р., Дашинимаев З.Б.</i> Исследование промерзания грунта с применением теплоизоляции из гранулированной пеностеклокерамики. Вестник Забайкальского государственного университета. 2019;25(7):34–44. https://doi.org/10.21209/2227-9245-2019-25-7-34-44
13. СП 25.13330.2020. Основания и фундаменты на вечномерзлых грунтах [интернет]. Москва; 2020. Режим доступа: https://www.minstroyrf.gov.ru/docs/117292/
14. СП 22.13330.2016. Основания зданий и сооружений. Актуализированная редакция СНиП 2.02.01-83* [интернет]. Москва; 2016. Режим доступа: https://www.minstroyrf.gov.ru/docs/14627/
15. Рекомендации по теплотехническим расчетам и прокладке трубопроводов в районах с глубоким сезонным промерзанием грунтов. Москва: НИИОСП; 1975.
16. Справочник по строительству на вечномерзлых грунтах. Ленинград: Стройиздат; 1977.
17. Рекомендации по учету и предупреждению деформаций и сил морозного пучения грунтов. Москва: Стройиздат; 1986.
18. Рекомендации по прогнозу теплового состояния мерзлых грунтов. Москва: Стройиздат; 1989.
19. СНиП 23-01-99. Строительная климатология [интернет]. Москва; 2006. Режим доступа: https://files.stroyinf.ru/Data2/1/4294849/4294849698.pdf
20. СНиП II-А. 6-72. Строительная климатология и геофизика [интернет]. Москва; 1973. Режим доступа: https://files.stroyinf.ru/Index2/1/4293828/4293828389.htm
Об авторе
А. Г. АлексеевРоссия
Андрей Григорьевич Алексеев, д-р техн. наук, руководитель центра геокриологических и геотехнических условий; доцент кафедры механики грунтов и геотехники
Рязанский проспект, д. 59, г. Москва, 109428, Российская Федерация; Ярославское шоссе, д. 26, г. Москва, 129337, Российская Федерация
e-mail: adr-alekseev@yandex.ru
Рецензия
Для цитирования:
Алексеев А.Г. Расчет глубины сезонного промерзания грунтов инженерными и численными методами. Вестник НИЦ «Строительство». 2024;42(3):56-82. https://doi.org/10.37538/2224-9494-2024-3(42)-56-82. EDN: RSJSVQ
For citation:
Alekseev A.G. Calculation of seasonal soil freezing depth by engineering and numerical methods. Bulletin of Science and Research Center of Construction. 2024;42(3):56-82. (In Russ.) https://doi.org/10.37538/2224-9494-2024-3(42)-56-82. EDN: RSJSVQ


























