Перейти к:
В развитие нормативного расчета на устойчивость изгибаемых элементов двутаврового постоянного и переменного сечений по СП 16.13330.2017
https://doi.org/10.37538/2224-9494-2025-1(44)-20-39
EDN: EAPXTJ
Аннотация
Введение. В настоящий момент нормы по стальным конструкциям (СП 16.13330.2017) содержат достаточно ограниченный материал в части расчета на устойчивость изгибаемых элементов. По-прежнему отсутствует какая-либо информация по расчету стержней переменного сечения на продольный и поперечный изгибы, как и на устойчивость таких элементов. Аналитические методы решения задач устойчивости продолжают оставаться востребованными и могут предложить более чем удобные решения в дополнение к численному анализу.
Цель. Развитие методики расчета на устойчивость изгибаемых элементов двутаврового постоянного и переменного сечений для улучшения раздела свода правил по стальным конструкциям в части устойчивости свода.
Материалы и методы. Разработка коэффициентов учета переменности поперечного сечения балки по длине, влияние градиента изгибающего момента аналитическим методом Бубнова – Галеркина. Альтернативная репрезентация изгибно-крутильной характеристики балки с учетом влияния места приложения нагрузки по высоте. Сравнение полученных аналитических решений в программных комплексах ЛИРА-САПР и ABAQUS.
Результаты. Проделанная аналитическая работа предлагает набор дополнительных коэффициентов и формул в поддержку развития методики расчета на устойчивость изгибаемых элементов. Решения находятся в согласии с философией СП 16.13330.2017. Результаты численного анализа подтверждают полученные аналитические решения.
Выводы. Текущее теоретическое исследование показало возможность улучшения существующего метода расчета балок на общую устойчивость. В статье выдвигается предложение о простой идее перегруппировки коэффициента устойчивости при изгибе и о превращении его в детерминированный для многих случаев (включая балки с переменной высотой стенки).
Ключевые слова
Для цитирования:
Ильюшенков А.О. В развитие нормативного расчета на устойчивость изгибаемых элементов двутаврового постоянного и переменного сечений по СП 16.13330.2017. Вестник НИЦ «Строительство». 2025;44(1):20-39. https://doi.org/10.37538/2224-9494-2025-1(44)-20-39. EDN: EAPXTJ
For citation:
Ilyushenkov A.O. On the SP 16.13330.2017 standard stability calculation of I-type bending elements with constant and variable cross-sections. Bulletin of Science and Research Center of Construction. 2025;44(1):20-39. (In Russ.) https://doi.org/10.37538/2224-9494-2025-1(44)-20-39. EDN: EAPXTJ
Подготовительная часть
Перед тем как приступить к непосредственному решению обозначенных задач, следует объяснить общие положения расчета. Для решения задачи об изгибаемом стержне, теряющем устойчивость по изгибно-крутильной форме, принимается система двух дифференциальных уравнений [1]. Уравнения определяют условие равновесия при действии закручивающих моментов при отсутствии сжимающей силы:
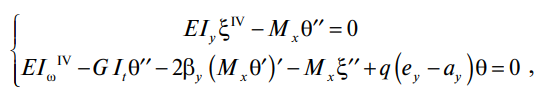 (1)
(1)
где Ely – наименьшая жесткость балки;
Elω – секториальная жесткость (жесткость при депланации);
GIt – жесткость при кручении;
βy – свойство асимметричности сечения;
ay – координата центра изгиба (по оси у);
q – интенсивность нагрузки, параллельной оси у;
θ – угол закручивания;
ξ – поперечное смещение;
ey – расстояние по высоте балки, на которой нагрузка прикладывается. Расстояние отсчитывается от центра изгиба и для симметричных профилей. Обычно ey = –0,5h, если нагрузка прикладывается к верхнему поясу, ey = +0,5h , если нагрузка прикладывается к нижнему поясу;
Mx – изгибающий момент или его функция по длине стержня.
В упругой стадии два дифференциальных уравнения устойчивости свободно опертой балки со свободной депланацией концевых сечений при действии нагрузки в плоскости симметрии могут быть приведены к одному. Во втором уравнении из системы двух можно исключить функцию ξ′′, если из первого уравнения выразить:
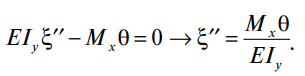 (2)
(2)
Первое уравнение системы из двух (1) может быть понижено в степени на два, исходя из граничных условий. При x = 0 и x = l вторая производная угла закручивания θ = θ′′ = 0. В соотвествии с этим получим диффренциальное уравнение изгибно-крутильной формы потери устойчивости шарнирно-опертой балки, загруженной поперечными силами Q, q и Mx.
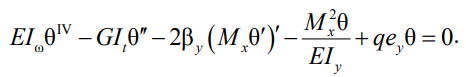 (3)
(3)
При этом для профиля, имеющего симметрию относительно оси y–y поперечного сечения, принимается ay = 0.
Дополнительно разберем производную произведения в третьем члене дифференциального уравнения (3). Согласно математическому правилу, производная произведения (uv)' = u'v + uv' , поэтому:
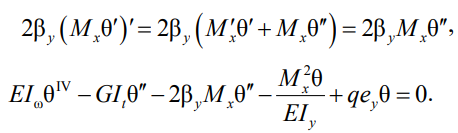 (4)
(4)
Под интенсивностью нагрузки нужно понимать не просто некоторую распределенную нагрузку q вдоль длины балки, но и возможные поперечные силы Qxk, действующие в точках с абсциссой xk. Поэтому, используя интеграл Римана – Стилтьеса, мы получим сумму интеграла для распределенной нагрузки qx и предел суммы поперечных сил Qxk. Так как интеграл Римана – Стилтьеса для функции f(x) по dx есть предел суммы функции f(x) на дельта разность Δx = x – xk, то:
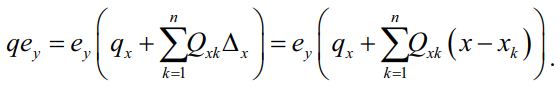
С другой стороны, из решения дифференциальных уравнений мы знаем, что вторая производная изгибающего момента , поэтому окончательно записываем:
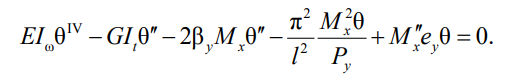 (5)
(5)
Если асимметрия в уравнении (5) отсутствует, тогда βy = 0:
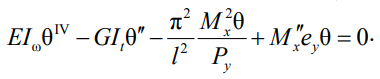 (6)
(6)
Коэффициент влияния градиента момента Cb
Изгибающий момент по концам стержня в большинстве случаев отличается от чистого изгиба. Являясь наиболее негативным, он, конечно же, предсказывает минимальное значение критического момента Mcr, которое можно считать безопасным, но и консервативным в то же самое время. В решаемых на практике задачах всегда поднимались и будут подниматься вопросы, связанные не только с экономией материалов, но и с точностью применяемых решений. На сегодняшний день существует достаточное количество численных формулировок и основанных на этом приближенных решений [2]. Однако точной аналитической формулировки до сих пор не представлено. Недостаточно иметь формулу, в которой не установлена четкая причинно-следственная связь, поэтому требуется привести такое честное аналитическое решение.
Данная проблема может быть решена при помощи аналитического аппарата метода Бубнова – Галеркина. Метод не только хорошо знаком отечественному инженеру, но и широко принят в решении большого числа задач устойчивости СП 16.13330.2017 [3]. Поэтому можно считать, что все дальнейшие действия не приведут к нарушению целостности философии документов [3][4].
Впервые в 1955 году Сальвадори [5] предложил простую модификацию уравнения Тимошенко [6] для учета эффекта градиента момента путем умножения его на некоторый коэффициент Cb:
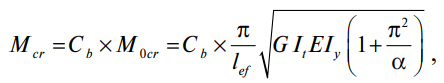 (7)
(7)
где M0cr – критический изгибающий момент при чистом изгибе;
Cb – коэффициент градиента изгибающего момента для всех случаев, кроме чистого изгиба.
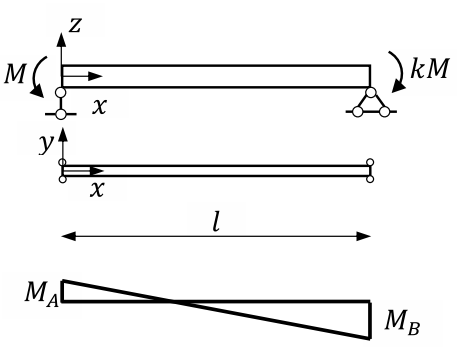
Рис. 1. Шарнирно-опертая балка, подверженная действию разных концевых изгибающих моментов
Fig. 1. A simply supported beam under various end bending moments
Для дальнейшей работы потребуется определить функцию изменения изгибающего момента по длине балки, показанной на рис. 1. При линейном изменении изгибающего момента следует использовать следующую зависимость:
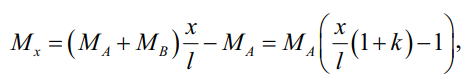 (8)
(8)
где 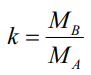 – отношение изгибающих моментов на концах стержня, которое изменяется в границах –1 ≤ k ≤ 1, k = –1 соответствует чистому изгибу.
– отношение изгибающих моментов на концах стержня, которое изменяется в границах –1 ≤ k ≤ 1, k = –1 соответствует чистому изгибу.
При решении задачи устойчивости методом Бубнова – Галеркина в общем случае принимается некоторый степенной ряд, отождествляемый с формой потери устойчивости:
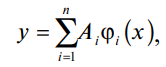 (9)
(9)
где Ai – неизвестные постоянные коэффициенты;
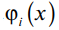 – функция, удовлетворяющая граничным условиям задачи.
– функция, удовлетворяющая граничным условиям задачи.
Для рассматриваемого случая (рис. 1), когда концы балки могут свободно закручиваться, для задания формы потери устойчивости предлагается традиционная синусоидальная зависимость для угла закручивания θ c n-количеством волн:
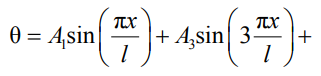
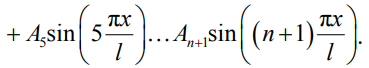 (10)
(10)
Числа n необязательно брать нечетными. Однако для последующих математических операций при удержании второго члена выгодно использовать нечетную функцию. Это позволит сократить количество слагаемых при неизвестных коэффициентах A1 и A3 и упростить раскрытие определителя матрицы.
Если θ(x) – точное решение задачи, то уравнение (6) будет равно нулю. Следовательно, функция в левой части этого уравнения будет ортогональной к любой функции, в том числе и к функциям (10) [7].
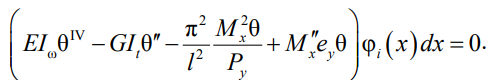 (11)
(11)
Сейчас и в дальнейшем ограничим ряд двумя первыми членами. И так как дифференциальное уравнение содержит производные второго и четвертого порядков (10), то:
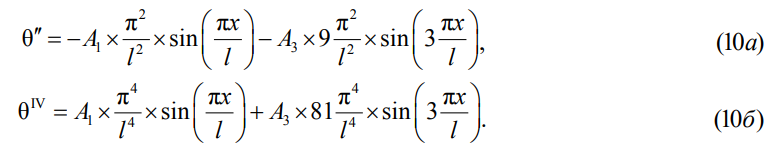
При этом вторая производная момента для (8) 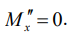
Сделаем попытку решить уравнение (11), используя только первый член ряда. Это приведет к возможности вычислять интегралы без необходимости составления определителя, так как рассматривается только одно алгебраическое уравнение. При этом неизвестный коэффициент A1 при подстановке функций (10а, б) в уравнение (11) сократится.
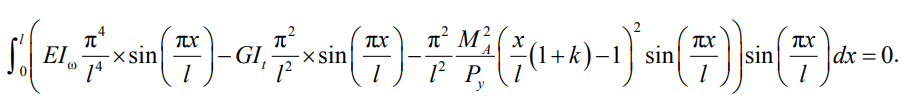 (12)
(12)
Вначале решаем часть уравнения, которая не связана с изгибающим моментом Mx. Для постоянного сечения интегралы секториальной и крутильной жесткостей решаются таблично с понижением степени:
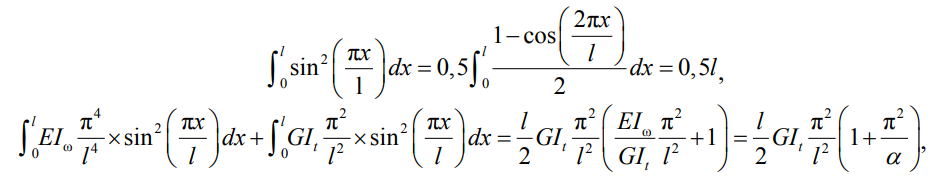 (13)
(13)
где a – нормативный обозначаемый коэффициент изгибно-крутильной характеристики балки.
Интеграл дифференциального уравнения (11), содержащий изгибающий момент Mx, решается значительно сложнее. Кроме понижения степени следует выполнить подстановку 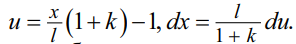 Затем произведения функций интегрируем по частям. В конечном итоге будет получена квадратичная функция. Для упрощения интегралы решаются, например, при помощи MATHCAD. Для удобства выделим отдельно и обозначим через произвольный коэффициент:
Затем произведения функций интегрируем по частям. В конечном итоге будет получена квадратичная функция. Для упрощения интегралы решаются, например, при помощи MATHCAD. Для удобства выделим отдельно и обозначим через произвольный коэффициент:
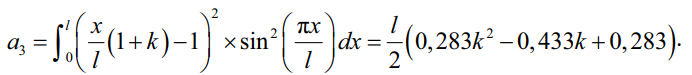 (14)
(14)
Тогда решение интеграла, содержащего функцию изменения изгибающего момента Mx по длине стержня:
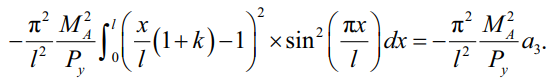 (15)
(15)
Собираем решения (13) и (15) воедино и выражаем изгибающий момент MA. При этом учтем, что в критической границе изгиба балки Mcr = MA, поэтому:
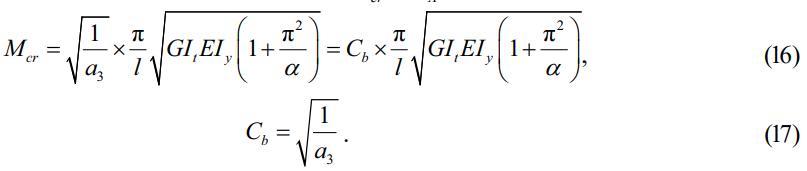
Проанализируем полученную функцию Cb(k). Для этого построим график (рис. 2) «k – Cb(k)» в границе –1 ≤ k ≤ 1. Максимальное значение Cb = 2,92 достигается при k = 0,75. Коэффициент Cb всегда больше единицы. Критический момент будет увеличиваться, а значит и устойчивость стержня будет повышена. Пунктиром на графике показана возможная аппроксимация уравнения (17).
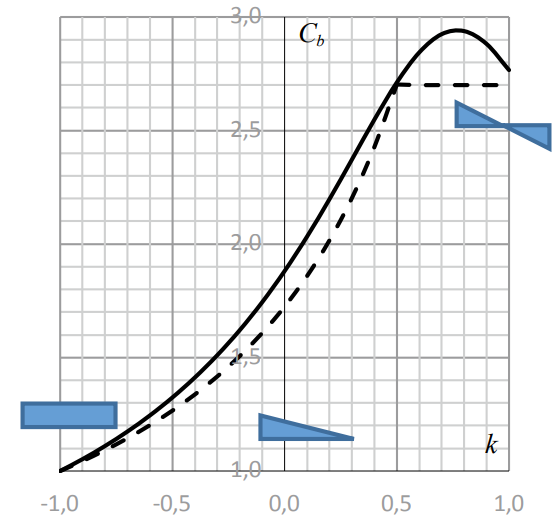
Рис. 2. График зависимости «k – Cb(k)» коэффициента градиента изгибающего момента Cb
Fig. 2. Dependence k – Cb(k) for the bending moment gradient coefficient Cb
Точная формулировка коэффициента изменения изгибающего момента по длине балки:
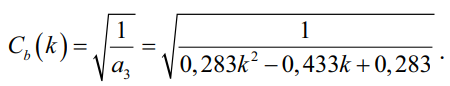 (18а)
(18а)
Приближенная формулировка образует нижнюю границу точного решения с выделением плато при k ≥ 0,5:
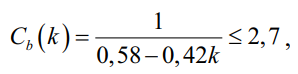 (18б)
(18б)
при 0,5 ≤ k ≤ 1, Cb = 2,7.
Тогда упругий коэффициент продольного изгиба балки φ1, согласно СП 16.13330.2017 [3], для любого сочетания изгибающих моментов, приложенных на концах балки:
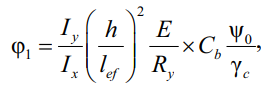 (19)
(19)
где 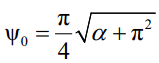 – функция от α при чистом изгибе;
– функция от α при чистом изгибе;
Cb – коэффициент изменения изгибающего момента по длине;
γc = 1,15 – коэффициент условий работы, учитывающий влияние геометрических несовершенств и принимаемый согласно [4, п. 7.2.2].
Произведем проверку полученного аналитического решения для градиента момента Cb по (18а). Для этого исследуем балку из двутавра 40Б1 длиной 5 м по ГОСТ Р 57837-2017 [8] в программном комплексе ЛИРА-САПР.
Расчетные характеристики балки: EIy = 2,06 × 1446,9 = 2980,6 кНм 2, EIω = 110,4 кНм 4. Нормы [3] рекомендуют принимать коэффициент при моменте инерции сечения при свободном кручении для двутаврового сечения с двумя осями симметрии k1 = 1,29.
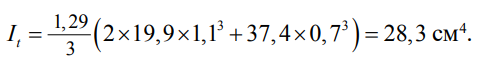
Модуль сдвига
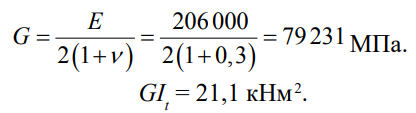
Критический изгибающий момент при чистом изгибе:
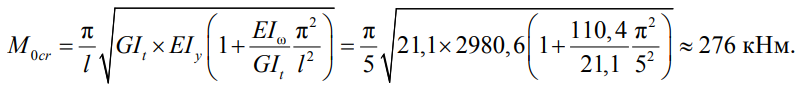
Далее путем умножения на коэффициент Cb получим диапазон значений критического момента Mcr по условию (16).
Значения коэффициента Cb, полученные численным способом, были вычислены следующим образом. Для каждого из случаев k от –1 до 1, с шагом 0,25 был определен коэффициент запаса устойчивости, по которому было найдено критическое значение изгибающего момента Mcr. Коэффициент виляния момента определялся из уравнения:
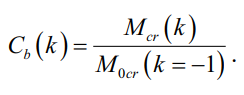
При расчете в ЛИРА-САПР следует обращать внимание на выбор конечного элемента стержня и признак схемы. Если проверка стержня на устойчивость выполняется с признаком схемы 5, то секториальная жесткость EIω не будет учтена. А формула, по которой вычисляется критический момент, соответствует уравнению:
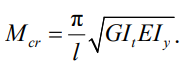
Для учета EIω расчеты следует производить с признаком схемы 6. Конечный элемент стержня с КЭ10 (по умолчанию) следует изменить на КЭ7. КЭ7 позволяет учитывать бимомент и создан для проверки в том числе и тонкостенных конструкций. Только в этом случае коэффициент запаса будет посчитан в полной степени.
Для сравнения результаты численного анализа и аналитического расчета сведем в табл. 1. Аналитическое решение, полученное при помощи метода Бубнова – Галеркина с одним членом ряда 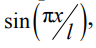 , совпадает с численным расчетом полностью.
, совпадает с численным расчетом полностью.
Учет переменности поперечного сечения балки по длине
Учет переменности по своему решению похож на вычисления, сделанные для коэффициента Cb. Будем считать, что ширина балки остается постоянной. Меняется только высота стенки.
Вначале потребуется определить функции изменения жесткости депланации и жесткости при кручении. В силу симметрии двутавра Iω = 0,25 Iy h2 можно предложить аналогичный Iy квадратичный закон изменения жесткости по длине и для секториальной жесткости Iω:
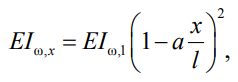 (20)
(20)
где 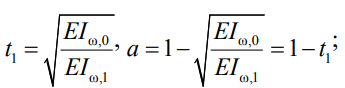 ;
;
EIω,1 – максимальная секториальная жесткость;
EIω,0 – минимальная секториальная жесткость.
Изменение EIy по длине стержня остается практически постоянным для двутавров с постоянной шириной полок, поэтому в целях экономии времени безопасно принимать постоянное значение. Используя это правильно EIy,0 = EIy,1, можно определить другое свойство t1:
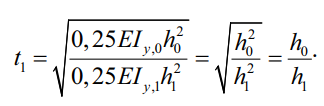 (21)
(21)
То есть функция изменения секториальной жесткости профиля (20) зависит только от высоты профиля на опорах. Для сварных двутавров h – tf – это расстояние между поясами. Для прокатных двутавров h – это полная высота профиля.
Решение интеграла секториальной жесткости в уравнении (11):
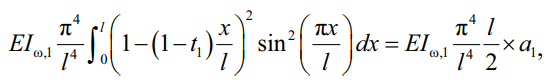 (22)
(22)
где 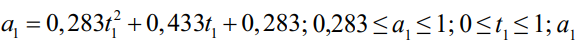 – коэффициент учета переменности при секториальной жесткости. Функцию можно аппроксимировать и привести к линейному алгебраическому уравнению. Однако потребуется ограничить границы t1 до практических.
– коэффициент учета переменности при секториальной жесткости. Функцию можно аппроксимировать и привести к линейному алгебраическому уравнению. Однако потребуется ограничить границы t1 до практических.
Как и для секториальной жесткости, составим закон изменения крутильной жесткости по длине. Ввиду того, что крутильная жесткость формируется из набора пластинок, закон изменения жесткости может представлять собой простую линейную зависимость следующего вида:
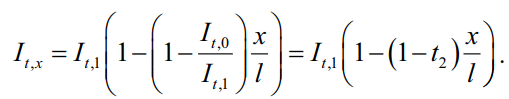 (23)
(23)
Решение интеграла жесткости при закручивании (11):
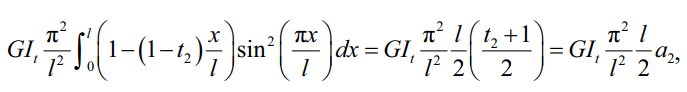 (24)
(24)
где 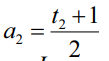 – коэффициент учета переменности при жесткости кручения;
– коэффициент учета переменности при жесткости кручения;
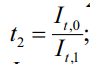
It,0 – минимальная крутильная жесткость;
It,1 – максимальная крутильная жесткость.
Если переменность заключена только в коэффициентах a1 и a2, удерживается только первый член ряда в методе Бубнова – Галеркина, тогда (22) и (24) интегрального решения дифференциального уравнения (11) складываются в характеристику балки переменного сечения:
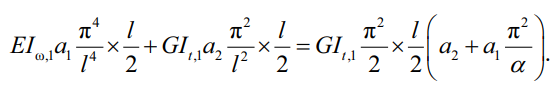 (25)
(25)
По мере приближения переменного сечения к постоянному (от конического к призматическому) оба коэффициента будут стремиться к единице a1, a2 → 1. И при постоянном сечении изгибно-крутильная жесткость вернется к своему изначальному выражению (13). А так как часть дифференциального уравнения (11), включающая в себя изгибающий момент Mx, уже рассмотрена, можно собрать уравнение критического момента для стержня переменной жесткости воедино:
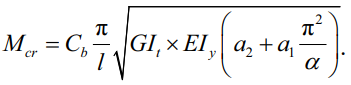 (26)
(26)
Таким образом, из (26) заключаем, что переменность шарнирно-опертой балки с учетом депланации и действующих изгибающих моментов на концах стержня определяется двумя редукционными коэффициентами a1 и a2.
В качестве примера исследуем двутавровый сварной профиль, показанный на рис. 3, со следующими принятыми геометрическими размерами: tf = 20 мм, bf = 200 мм, hw,1 = 900 мм,
hw,0 = 400 мм, tw = 8 мм. Пролет балки составляет l = 6000 мм.
Таблица 1
Сравнительная таблица значений критического момента Mcr шарнирно-опертой балки 40Б1, l = 5 м
Table 1
Comparison of critical moment Mcr values for a 40B1 simply supported beam, 40B1, l = 5 m
k | Cb | Mcr, кНм | ||
ЛИРА-САПР | (18а) | Cb × M0cr (16) | ЛИРА-САПР | |
–1 | 1,00 | 1,00 | 276 | 284 |
–0,75 | 1,14 | 1,14 | 315 | 324 |
–0,5 | 1,32 | 1,32 | 365 | 375 |
–0,25 | 1,56 | 1,56 | 432 | 442 |
0 | 1,86 | 1,88 | 519 | 527 |
0,25 | 2,23 | 2,28 | 629 | 632 |
0,5 | 2,62 | 2,70 | 745 | 744 |
0,75 | 2,88 | 2,92 | 805 | 818 |
1 | 2,75 | 2,74 | 757 | 782 |
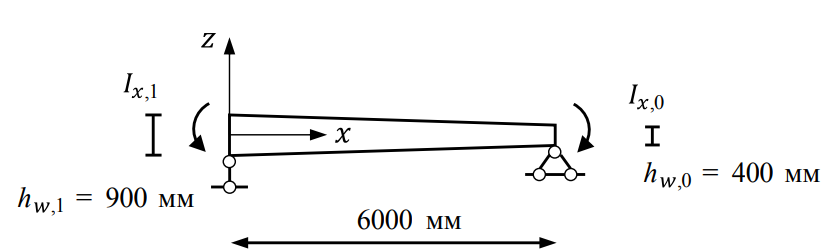
Рис. 3. Исследуемая балка переменного сечения
Fig. 3. Studied variable cross-section beam
Подсчитываем необходимые характеристики сечений двутавра на опорах.
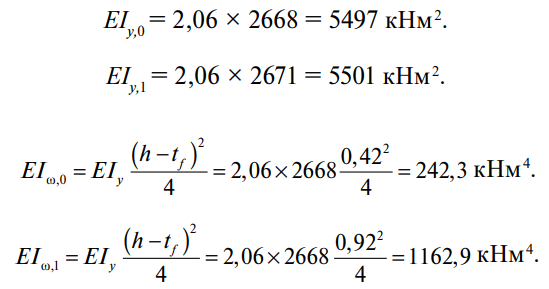
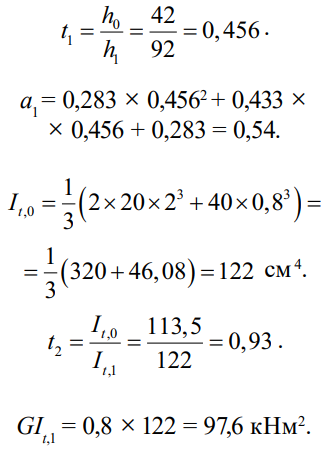
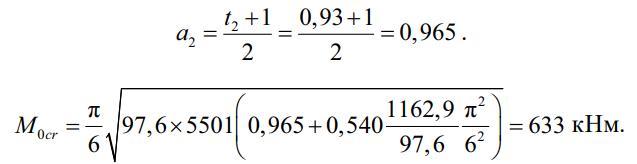
Для такой же балки, но постоянного сечения при высоте стенки hw,1 = 900 мм, M0cr = 784 кНм. Уменьшение критического момента из-за переменности составляет 20 %.
Для проверки формулы (26) создадим конечно-элементную модель балки в программном комплексе ABAQUS. Материал балки бесконечно упругий. Модуль упругости E = 206 000 МПа. Коэффициент Пуассона v = 0,03.Тип конечного элемента оболочки – S4R, Quad-Dominated Structured. Размер конечного элемента принят 25 мм. Тип расчета: Linear Perturbation – Buckle. На рис. 4 показана конечно-элементная модель балки и форма потери устойчивости при чистом изгибе. Пробные расчеты показали, что размер конечного элемента в 25 мм показывает идентичные результаты критического момента Mcr, как и при частой сетке в 10 мм. Кинематика балки приведена на рис. 5. На опорах нижний пояс балки имеет закрепление по Z. Верхний пояс закреплен от смещения поперек по оси Y. Дополнительно задана связь одного конечного элемента по X. Для исключения искажения торцов балки и появления более высоких мод местной формы потери устойчивости на опорах были смоделированы ребра жесткости толщиной 10 мм. Для чистого изгиба по концам в точках приложены пары сил со значениями –0,5 слева и 0,5 справа. Остаточные напряжения не прикладывались. Геометрическое несовершенство не вводилось.
В целях апробации уравнения (26) момент на левом конце балки варьировался. По результатам численного расчета составлена сравнительная табл. 2.

Рис. 4. Конечно-элементная модель и потеря устойчивости балки переменного сечения в ABAQUS
Fig. 4. ABAQUS finite element model and buckling of a variable cross-section beam

Рис. 5. Кинематика балки
Fig. 5. Beam kinematics
Таблица 2
Сравнительная таблица результатов аналитического и численного расчетов балки переменного сечения
Table 2
Comparison of analytical and numerical solution results for a variable cross-section beam
k | Cb | (26) Cb M0cr, кНм | ABAQUS Mcr , кНм |
–1 | 1 | 633 | 562 |
–0,5 | 1,32 | 835 | 710 |
0 | 1,86 | 1177 | 1020 |
Несмотря на удовлетворительные результаты расчетов, приведем дополнительное решение с удержанием двух членов ряда в короткой форме записи. При удержании второго члена при решении задачи методом Бубнова – Галеркина приходим к системе из двух алгебраических уравнений с неизвестными постоянными A1 и A3:
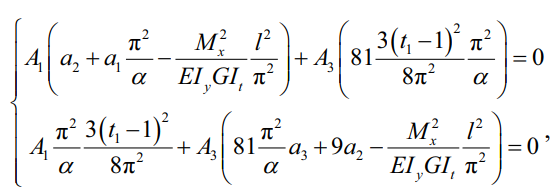 (27)
(27)
где 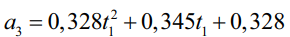 – новая дополнительная функция.
– новая дополнительная функция.
При неизвестных в системе уравнений (27) составляем определитель 2 × 2:
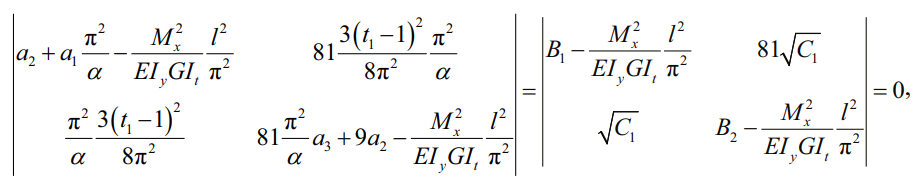
вводим сокращенные обозначения:
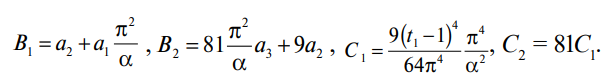
Раскрываем определитель путем перемножения левой и правой диагоналей по следующему правилу:
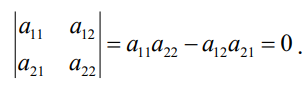
Опуская математические операции, получим полное квадратное уравнение, наименьший корень которого:
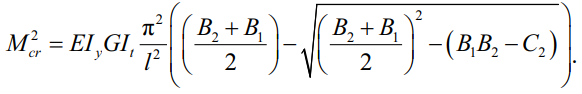 (28)
(28)
Очевидно, что при удержании двух и более членов ряда коэффициент Cb неизбежно оказывается связан с коэффициентом α. При этом, как это было показано в работах Чувикина [9] и Броуде [10], уточнения коэффициента Cb для шарнирно-опертых балок не происходит. В целях проверки и сравнения (26) и (28) дополнительно были посчитаны еще три балки. Отличия в коэффициентах a1 и a2 составляют сотые доли. Поэтому можно считать, что расчеты с удержанием только первого члена оказываются достаточно точными. Также следует уточнить, что бо́льшую точность возможно получить, если учесть точную форму прогиба стержня с переменной высотой стенки. Расхождение результатов критического момента между формулой (26) и расчета в ABAQUS объясняется принятием в качестве базисной функции тригонометрического ряда синуса. С ростом переменности линия прогиба становится явно асимметрична относительно середины пролета и максимальное значение смещается в сторону наименьшего поперечного сечения. Поэтому данный способ следует считать приближенным. Применимость формулы (26) должна ограничиваться умеренным углом наклона поясов β = 3–4°. При большем угле наклона поясов необходимо искать другую базисную функцию, способную отражать асимметричность.
Альтернативная репрезентация ψ в формуле коэффициента продольного изгиба φ1
Решим нормативную задачу для равномерно распределенной нагрузки, приложенной к верхней (сжатой) полке шарнирно-опертой балки. Используем следующие подстановки:
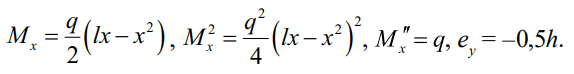
Решения интегралов, не связанные с внешними воздействиями, остаются прежними по (13). Выполним подстановку Mx, Mx2 и в уравнение (5), удерживая только первый член ряда (10):
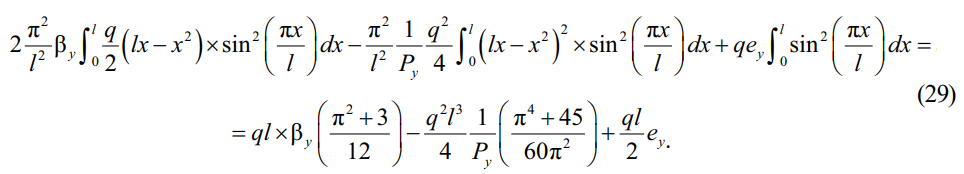
Суммируем решения интегралов, соединяя воедино (13) и (29):
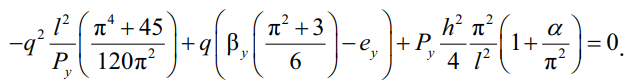 (30)
(30)
Складывая полученные части после интегрирования, приходим к полному квадратному уравнению, где за неизвестное принимаем равномерно распределенную нагрузку q. Так как критический момент всегда должен быть больше нуля Mcr > 0, то для последующего изучения упругой формы потери устойчивости балки под действием q следует оставить только положительный корень:
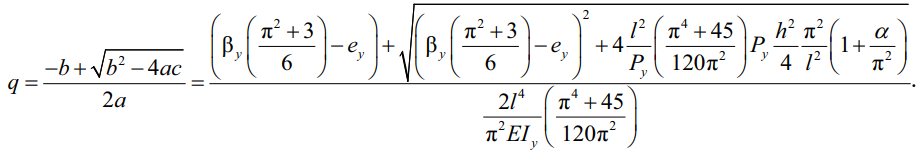 (31)
(31)
Коэффициент при q обозначим, как и в нормах, через B. Коэффициент B – это коэффициент, учитывающий место приложения внешней поперечной нагрузки q или Q по высоте поперечного сечения h и асимметрию поперечного сечения βy. Учитывая, что реалистично нагрузки прикладываются либо к верхнему, либо к нижнему поясу, а промежуточные значения остаются достаточно редкими, будем считать, что ey = ±0,5h. Поэтому для рассматриваемого случая:
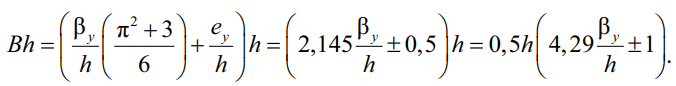 (32)
(32)
Или в сокращенной форме:
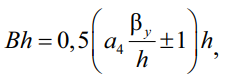 (33)
(33)
где a4 – коэффициент вида поперечной нагрузки;
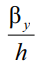 – асимметричное свойство поперечного сечения.
– асимметричное свойство поперечного сечения.
Если асимметрия или ее влияние отсутствует либо игнорируется, тогда коэффициент B упрощается до:
Bh = ± eyh = ± 0,5h. (34)
В подкоренном выражении 4ac упрощается до выражения:
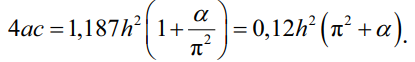 (35)
(35)
Данная часть уравнения обозначается через коэффициент C и в общем случае всегда записывается как:
Ch2 = a5h2D, (36)
где a5 – коэффициент, зависящий от вида поперечной нагрузки;
D = π2 +α – константа для любых случаев, крутильная характеристика поперечного сечения.
Знаменатель корня квадратного уравнения 2a может быть также приведен к компактному виду:
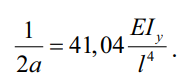 (37)
(37)
Учитывая введенные сокращенные обозначения (33), (35) и (36), перепишем (31):
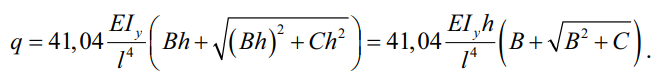 (38)
(38)
Теперь выражение следует привести к максимальному значению изгибающего момента, то есть к его критическому значению. Для равномерно распределенной нагрузки при шарнирном закреплении балки на концах:
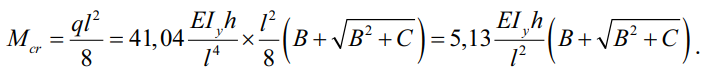 (39)
(39)
Критические напряжения для двутавровой симметричной балки [10]:
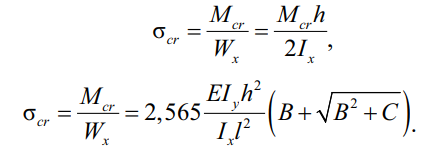 (40)
(40)
Число 2,565 является другим коэффициентом поперечной нагрузки A = 2,565. Тогда окончательно в общей и нормативной формах записи уравнение критического момента потери устойчивости балки при изгибе с кручением:
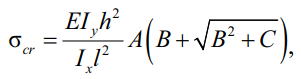 (41)
(41)
а коэффициент изгиба с кручением балки в упругой области напряжений:
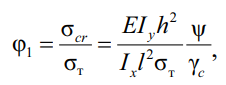
где 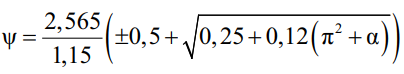 – изгибно-крутильная характеристика балки.
– изгибно-крутильная характеристика балки.
Теперь создадим альтернативную формулировку коэффициента ψ. Идея репрезентативности ψ заключена в том, чтобы получить общее и интуитивно понятное уравнение, которое будет применительно к любому другому случаю. Как известно, коэффициент ψ ранее был записан в табличной форме [10]. В сегодняшних нормах этот коэффициент был аппроксимирован и приведен в виде полиномиальной зависимости, которая, по правде сказать, достаточно плохо представляется инженеру, потому как теряется причинно-следственная связь вычисления α, но ситуацию можно исправить. Вся проблема заключена лишь в том, что формулы в [3, табл. Ж.1] были составлены как функции ψ(α). В то время как они должны были быть составлены от 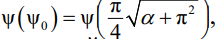 то есть от чистого изгиба. Не секрет, что такая зависимость будет иметь линейное представление в форме алгебраического уравнения общего вида:
то есть от чистого изгиба. Не секрет, что такая зависимость будет иметь линейное представление в форме алгебраического уравнения общего вида:
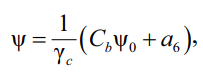 (42)
(42)
где ψ0 – функция от чистого изгиба;
Cb – коэффициент влияния момента или внешней нагрузки в общем случае;
a6 – коэффициент, учитывающий место приложения поперечной нагрузки по высоте сечения.
Альтернативная репрезентация способна предоставить больше гибкости в расчетах, как и упростить табл. Ж.1, приведенную в своде правил по стальным конструкциям [3].
При приложении равномерно распределенной нагрузки к верхнему (сжатому) поясу с учетом коэффициента условий работы γc = 1,15:
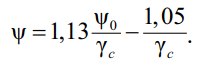 (43)
(43)
При приложении нагрузки к нижнему поясу (растянутому):
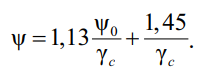 (44)
(44)
Соответственно, если нагрузка прикладывается к оси или центру тяжести поперечного сечения (совпадающего для симметричного двутавра с центром изгиба), тогда следует очевидное:
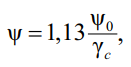 (45)
(45)
где Cb = 1,13.
В виде неполного квадратного уравнения можно установить влияние приложения нагрузки по высоте сечения по трем точкам. При ey = – 0,5, a6 = –1,05. При ey = 0, a6 = 0. При ey = +0,5, a6 = +1,45. Тогда алгебраическое уравнение, построенное от центра тяжести поперечного сечения:
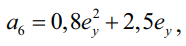 (46)
(46)
где ey – ордината приложения нагрузки по высоте сечения в границах –0,5 < ey < 0,5.
Такое неполное уравнение всегда имеет пологий вид на графике (рис. 6), поэтому в целях упрощения уравнение может быть подвергнуто линеаризации.
Для проверки правильности приведенных формул составлена сравнительная табл. 3, где указаны числовые значения ψ в зависимости от параметра α.
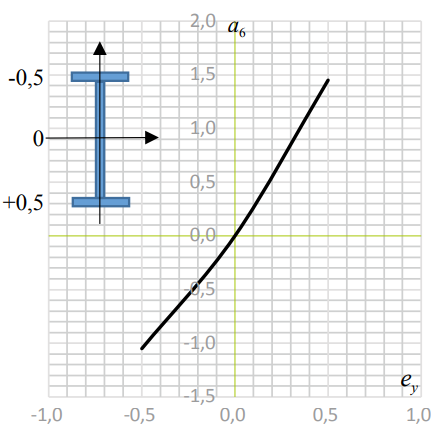
Рис. 6. График зависимости «a6 – ey»
Fig. 6. Dependence a6 – ey
Таблица 3
Сравнительная таблица коэффициента ψ
Table 3
Comparative table of ψ coefficient values
α | Сжатый пояс | Растянутый пояс | Сжатый пояс | Растянутый пояс |
[1, табл. Ж.1] | (43) | (44) | ||
0,1 | 1,61 | 3,81 | 1,52 | 3,70 |
0,4 | 1,63 | 3,83 | 1,56 | 3,73 |
1 | 1,68 | 3,88 | 1,63 | 3,80 |
4 | 1,92 | 4,12 | 1,96 | 4,13 |
8 | 2,24 | 4,44 | 2,35 | 4,52 |
16 | 2,88 | 5,08 | 3,01 | 5,18 |
24 | 3,52 | 5,72 | 3,58 | 5,75 |
32 | 4,16 | 6,36 | 4,08 | 6,25 |
40 | 4,80 | 7,00 | 4,53 | 6,71 |
48 | 5,01 | 7,21 | 4,95 | 7,13 |
64 | 5,60 | 7,80 | 5,72 | 7,89 |
80 | 6,18 | 8,38 | 6,40 | 8,57 |
96 | 6,74 | 8,94 | 7,02 | 9,20 |
128 | 7,83 | 10,03 | 8,14 | 10,32 |
160 | 8,86 | 11,06 | 9,14 | 11,31 |
240 | 11,19 | 13,39 | 11,28 | 13,45 |
320 | 13,19 | 15,39 | 13,10 | 15,27 |
400 | 14,83 | 17,03 | 14,70 | 16,88 |
Оставляя дальнейшую математическую работу за рамками статьи, для сосредоточенной силы при шарнирном опирании балки: Cb = 1,35, a6 = +3,76ey. Коэффициент приложения нагрузки a6 возможно упростить и подвести к одному обобщенному выражению для всех случаев. К примеру, нормы США [2] предлагают упрощенный подход, согласно которому учет места приложения поперечной нагрузки определяется путем модификации коэффициента влияния момента Cb:
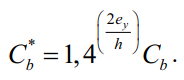 (47)
(47)
Формула (47) является достаточно приближенным решением, в особенности для равномерно распределенной нагрузки. Однако такая унификация позволяет получить гибкое и универсальное уравнение применительно к широкому набору случаев приложения поперечных нагрузок к балке.
Заключение
Проделанная теоретическая работа позволяет оценить потенциал и возможности по развитию раздела устойчивости изгибаемых элементов, как минимум, двутаврового сечения. Как это было продемонстрировано, аналитические методы решения задач в современной системе проектирования стальных конструкций ни в коем случае нельзя списывать со счетов. Документам [3][4] есть куда расти. Существует вполне четкая уверенность в возможности развития разделов устойчивости, решении вопросов колонн переменного сечения, изгибно-крутильной формы потери устойчивости и эффективных или расчетных длин.
Список литературы
1. <i>Власов В.З.</i> Тонкостенные упругие стержни. Москва: Физматлит; 1959.
2. ANSI/AISC 360-22. Specification for Structural Steel Buildings [internet]. American Institute of Steel Construction; 2022. Available at: https://www.aisc.org/globalassets/product-files-not-searched/publications/standards/a360-22w.pdf.
3. СП 16.13330.2017. Стальные конструкции. Актуализированная редакция СНиП II-23-81*. Москва: Минстрой России; 2017.
4. СП 294.1325800.2017. Конструкции стальные. Правила проектирования. Москва: Минстрой России; 2017.
5. <i>Salvadori M.G.</i> Lateral buckling of I-beams. Transactions of the American Society of Civil Engineers. 1955;120(1). https://doi.org/10.1061/taceat.00072286.
6. <i>Тимошенко С.П.</i> Устойчивость упругих систем. Москва: Гостехиздат; 1946.
7. <i>Масленников А.М.</i> Динамика и устойчивость сооружений. Москва: Юрайт; 2017.
8. ГОСТ Р 57837-2017. Двутавры стальные горячекатаные с параллельными гранями полок. Технические условия. Москва: Стандартинформ; 2019.
9. <i>Чувикин Г.М.</i> Об устойчивости за пределом упругости внецентренно сжатых тонкостенных стержней открытого профиля. В: Исследования по стальным конструкциям. Москва: Госстройиздат; 1962.
10. <i>Броуде Б.М.</i> Предельные состояния стальных балок. Москва: Стройиздат; 1953.
Об авторе
А. О. ИльюшенковРоссия
Александр Олегович Ильюшенков, инженер промышленного и гражданского строительства
ул. Уссурийский бульвар, д. 2, г. Хабаровск, 680000, Российская Федерация
e-mail: revivaltree@gmail.com
Рецензия
Для цитирования:
Ильюшенков А.О. В развитие нормативного расчета на устойчивость изгибаемых элементов двутаврового постоянного и переменного сечений по СП 16.13330.2017. Вестник НИЦ «Строительство». 2025;44(1):20-39. https://doi.org/10.37538/2224-9494-2025-1(44)-20-39. EDN: EAPXTJ
For citation:
Ilyushenkov A.O. On the SP 16.13330.2017 standard stability calculation of I-type bending elements with constant and variable cross-sections. Bulletin of Science and Research Center of Construction. 2025;44(1):20-39. (In Russ.) https://doi.org/10.37538/2224-9494-2025-1(44)-20-39. EDN: EAPXTJ


























