Перейти к:
Способ повышения прочности и долговечности тонкостенных элементов металлических конструкций
https://doi.org/10.37538/2224-9494-2025-1(44)-75-83
EDN: LXCJHG
Аннотация
Введение. Обилие подходов численного моделирования, инженерных решений, включая использование технических программных комплексов, не дало возможности найти рациональный универсальный метод повышения такого значимого параметра, как износоустойчивость строительных конструкций, что делает актуальными исследования в данной области.
Цель. Проведение испытаний конструктивных элементов с заданными параметрами для оценки возможных вариантов применения искусственно созданных материалов (упругие, низкомодульные) с целью демпфирования конструкций, включая их компоненты на примере металлических мостовых балок.
Материалы и методы. В ходе исследования применялись численные методы оценки на основе параметрического анализа консольной балки и балки мостового крана (решение дифференциальных уравнений второго порядка). Частотный анализ балки проводился путем компьютерного моделирования в программной среде SolidWorks. Проводилось сравнение полученных значений показателей логарифмического понижения прочности металлических мостовых конструкций с общепринятыми справочными величинами в определенных диапазонах. В качестве исходных данных в численных расчетах фигурировали такие показатели, как грузоподъемность мостового крана – 20 тонн, пролет – 19,5 метров. Исходные размеры поперечного сечения стальной мостовой балки были выбраны на основе предложенной методики В.Е. Дусье, Ю.В. Наварского, В.П. Жегульского: H = 1,1 м; b = 0,6 м; S = 9 мм.
Результаты. Численное и компьютерное моделирование продемонстрировало возможность увеличения срока службы элементов конструкций технического оборудования, демпфируемых изоляционным материалом. Была определена необходимость тестирования усталостных характеристик наполнителя, его адгезии к металлу. Поиск рационального решения возможен при условии детального изучения схемы размещения изоляционного материала внутри конструкции.
Выводы. С точки зрения задач оптимизации необходимо проводить оценку стоимости проекта. В то же время представленные результаты показали, что такой способ демпфирования имеет хорошие перспективы с точки зрения повышения прочности и долговечности элементов металлических конструкции.
Ключевые слова
Для цитирования:
Серых А.А. Способ повышения прочности и долговечности тонкостенных элементов металлических конструкций. Вестник НИЦ «Строительство». 2025;44(1):75-83. https://doi.org/10.37538/2224-9494-2025-1(44)-75-83. EDN: LXCJHG
For citation:
Serykh A.A. Method for increasing the strength and durability of thin-walled elements in metal structures. Bulletin of Science and Research Center of Construction. 2025;44(1):75-83. (In Russ.) https://doi.org/10.37538/2224-9494-2025-1(44)-75-83. EDN: LXCJHG
Проблема увеличения долговечности конструкций (элементов, изделий) остается актуальной для многих отраслей, несмотря на наличие множества различных подходов. Тонкостенные конструктивные элементы подвержены изменениям, что приводит к формированию усталостных трещин на поверхности [1]. Такие преобразования влекут за собой барьеры при реализации на практике, однако за счет уменьшения колебаний конструктивных элементов и изделия в целом увеличивается параметр долговечности, например с помощью различных виброгасителей [2]. В строительной отрасли, авиастроении повышение долговечности конструктивных элементов реализуется за счет использования трехслойных плит и оболочек [3].
Коробчатые балки и стержни с тонкими стенками из замкнутых профилей находят широкое применение в конструкциях технических средств для горнодобывающей промышленности и транспортной сферы (оборудование, машины). Эксплуатация технических средств проходит в режиме воздействия обширного диапазона высоких рутинных и пиковых внезапных динамических нагрузок.
Увеличение долговечности технических средств, в том числе формирование комфортной рабочей среды обслуживающего персонала, напрямую зависит от снижения активности возникающих нагрузок. Реализация защитных функций сотрудников от негативного воздействия (шум, вибрации) достигается путем применения легковесных теплоизоляционных материалов (ППТ), препятствующих разрушению, ржавлению (коррозия). Приоритетной функцией наполнителя является поглощение энергии вибрации, в том числе снижение динамики внешних нагрузок (амплитуда, количество).
Целью статьи является поиск рациональных решений применения искусственно созданных материалов (упругие, низкомодульные) с целью демпфирования конструкций, включая их компоненты на примере металлических мостовых балок. Для реализации прочностного анализа и вычислительного эксперимента был использован программный комплекс SolidWorks.
В целях исследования проводились испытания балок из стали со следующими характеристиками: длина l = 600 мм, ширина коробчатого сечения b = 25 мм, высота H = 70 мм, толщина стенки S = 1,5 мм.
Определение таких параметров, как износоустойчивость и прочность компонентов несущих конструкций технического оборудования, напрямую связано с определением ключевого аспекта – с оценкой напряжений при изгибе. В работе будет допущено предположение о наличии только свободных колебаний балок, которые подвергаются изгибу. Поиск рациональных решений предполагает последовательность следующих шагов:
– определение числа циклов свободной вибрации с существенным затуханием;
– параметрический анализ консольной балки;
– параметрический анализ балки мостового крана.
Оценочные расчеты позволяют рассматривать колебания балки как материальную точку с уменьшенной массой mp на пружине эквивалентной жесткости cе. Однородные дифференциальные уравнения второго порядка позволяют описать свободные колебания материальной точки [4]. Если пренебречь силами сопротивления, то можно искать решения следующего уравнения:
x’’ + p2 × x = 0 (1)
где p 2 = cе/mp – квадрат угловой частоты;
cе – жесткость стальной балки;
mp – пониженная жесткость балки без наполнителя.
Для точки T = 1/ω свободные гармонические колебания будут иметь частоту ω = ρ/2π.
Если на систему оказывают влияние силы низкого сопротивления, соразмерные скорости перемещения первой степени R = αx, то для изделий из конструктивных элементов будет действовать уравнение:
x’’ + 2n × x’ + p12 × x = 0, (2)
где n = α/2mpr;
α – коэффициент сопротивления, уменьшенная масса балки с изоляционным материалом;
mpr – уменьшенная масса балки с изоляционным материалом;
p12= cеr/mpr – квадрат угловой частоты для балки с изоляционным материалом;
cеr – эквивалентная жесткость балки с изоляционным материалом.
Тогда свободные затухающие колебания будут характеризоваться частотой ω1 = p1/2π, условный период T1 = 2π/p1, в свою очередь угловая частота будет определяться следующим образом: 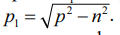
Эмпирическая информация тождественна входным параметрам для оценки констант на основе дифференциальных уравнений. Следующие равенства x = x0, x’0 = 0 справедливы при t = 0.
Получаем выражение для затухающих колебаний балки с постепенно уменьшающейся амплитудой в течение n ˂ p1. Огибающие кривой процесса определяются функциями:
x = ± x0 × e-nt. (3)
Оценить амплитуду вибрации позволяет простое выражение x/x0 ≥ 0,1, независящее от величины исходного смещения x0. Выражения (3) и (4) дают возможность рассчитать необходимое время t:
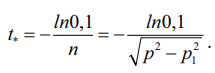 (4)
(4)
Предполагаемое количество весомых циклов N рассчитывается по формуле, в том числе для известных частот p и p1:
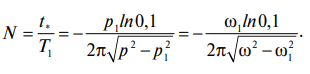 (5)
(5)
Инновационные интеллектуальные системы дают возможность оценить собственные частоты ω, ω1 для компонентов с тонкими стенками различной конфигурации.
Подбор ширины стенки S и высоты слоя термоизоляционного материала h для металлической балки осуществляем на основе энергетического анализа, обозначая их переменными параметрами.
Используя программную среду SolidWorks, проводим частотный анализ консольной балки в исходном состоянии и с пенопластовым наполнителем [5]. Для проведения частотного анализа были построены твердотельная модель коробчатой балки и сборочная модель, заполненная пенопластом.
Предположим, что ω – это собственная частота балки без наполнителя, а ω1 – частота балки с наполнителем, и проведем оценку демпфирующего эффекта, который оказывают пенопласты, на основе выражения (6).
Определяем наименьшие частоты колебаний балок в исходном состоянии или с пенопластовым наполнителем для интервала S ∈ [ 0,2; 1,5] мм.
На рис. 1 отражена зависимость количества циклов вибрации от толщины стенки балки с наполнителем. При этом число весомых колебаний связано с толщиной стенки конкретным сегментом балки.
Справочные издания содержат информацию о логарифмическом снижении прочности металлических мостовых конструкций в диапазоне δ = 0,05–0,12. При заданном уровне значимости 0,1 число свободных колебаний ограничено диапазоном 19–49 циклов. Результаты численных экспериментов демонстрируют тождественность числа колебаний интервалу 11–33 цикла. Этот показатель ниже величины числа колебаний на 30 % по сравнению с коробчатой балкой. Полученные данные обозначим термином «весомые». Проведенные расчеты о предполагаемом числе циклов для балки, наполненной изоляционным материалом, требуют валидационной проверки.
В качестве исходных данных в численных расчетах фигурировали такие показатели, как грузоподъемность мостового крана – 20 тонн, пролет – 19,5 метров. Исходные размеры поперечного сечения стальной мостовой балки были выбраны на основе предложенной методики [6]: H = 1,1 м; b = 0,6 м; S = 9 мм.
Форма изгибных колебаний для балки зависит от ее крепления при определенных выбранных условиях.
Логарифмическое уменьшение амплитуды колебаний δ связано с коэффициентом демпфирования n, который определяется из выражения (3) как δ = T1n. Его значения определены в справочниках. В табл. 1 и 2 приведены значения декремента, рассчитанные для балок моста с различной высотой слоя наполнителя H.
Таблица 1
Логарифмическое уменьшение свободных затухающих колебаний δ в горизонтальной плоскости
Table 1
Logarithmic decrement δ of free damped oscillations in the horizontal plane
Толщина стенки, s, мм | Высота слоя шпатлевки, мм | ||||
220 | 440 | 660 | 880 | 1100 | |
4 | 0,158 | 0,176 | 0,190 | 0,207 | 0,231 |
5 | 0,134 | 0,152 | 0,168 | 0,182 | 0,207 |
6 | 0,116 | 0,134 | 0,151 | 0,168 | 0,189 |
7 | 0,091 | 0,109 | 0,128 | 0,145 | 0,174 |
8 | 0,070 | 0,094 | 0,115 | 0,129 | 0,160 |
9 | 0,053 | 0,081 | 0,100 | 0,113 | 0,146 |
10 | 0,049 | 0,074 | 0,094 | 0,109 | 0,137 |
Таблица 2
Логарифмический декремент свободных затухающих колебаний δ в вертикальной плоскости
Table 2
Logarithmic decrement δ of free damped oscillations in the vertical plane
Толщина стенки, s, мм | Высота слоя шпатлевки, мм | ||||
220 | 440 | 660 | 880 | 1100 | |
4 | 0,124 | 0,173 | 0,203 | 0,233 | 0,251 |
5 | 0,099 | 0,145 | 0,173 | 0,197 | 0,222 |
6 | 0,089 | 0,125 | 0,152 | 0,177 | 0,194 |
7 | 0,081 | 0,127 | 0,149 | 0,169 | 0,184 |
8 | 0,076 | 0,111 | 0,137 | 0,153 | 0,171 |
9 | 0,067 | 0,100 | 0,122 | 0,143 | 0,158 |
10 | 0,065 | 0,098 | 0,118 | 0,133 | 0,152 |
На рис. 2 показаны графики изменения коэффициента сжатия в зависимости от выбранных параметров. Демпфирующая способность компонентов технического оборудования повышается с уменьшением толщины стенки и увеличением высоты слоя изоляционного материала.
Соответственно снижается число весомых циклов. На рис. 3 демонстрируется взаимосвязь числа циклов, толщины стенки балки и высоты демпфирующего слоя в определенных диапазонах.
Для прошедшей испытания в лабораторных условиях балки (рис. 1) и балки моста (рис. 3) сделан прогноз получения значительного демпфирующего эффекта от использования в качестве наполнителей легких низкомодульных пенопластов. Результаты исследований показали снижение количества колебаний в обеих плоскостях (горизонтальная, вертикальная) при повышении значения высоты слоя изолирующего материала. Заданная толщина стенки составляла 9 мм.
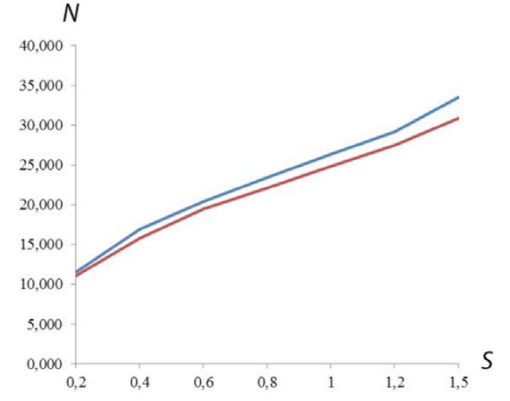
Рис. 1. Графическая интерпретация соотношения количества циклов вибрации N от толщины стенки металлической балки S: синяя линия (верхняя) – горизонтальная плоскость; красная (нижняя) – вертикальная плоскость
Fig. 1. Number of vibration cycles N taken relative to the wall thickness of a metal beam S: blue line (upper) – horizontal plane; red (lower) – vertical plane
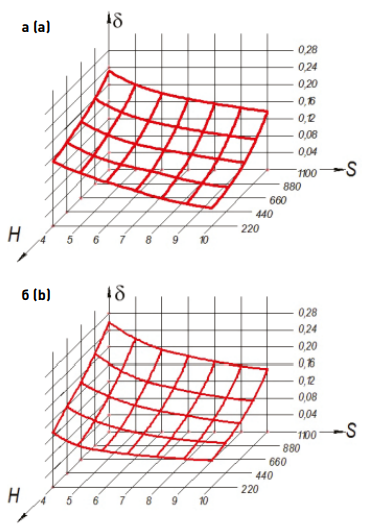
Рис. 2. График изменения коэффициента сжатия в зависимости от толщины стенки и высоты слоя изоляционного материала: а – горизонтальная плоскость; б – вертикальная плоскость
Fig. 2. Change in the compression coefficient depending on the wall thickness and the height of the insulating layer: a – horizontal plane; b – vertical plane
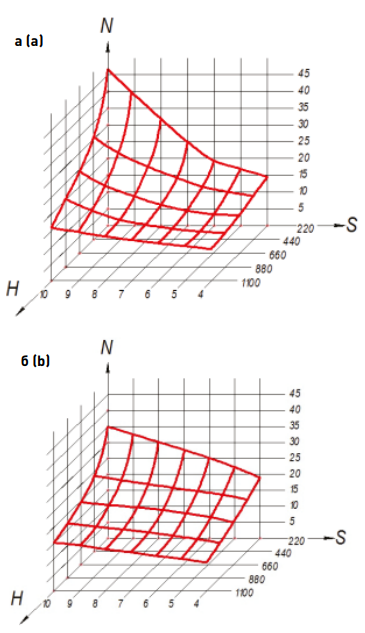
Рис. 3. График зависимости весомых колебаний балки от заданных исходных параметров: а – горизонтальная плоскость; б – вертикальная плоскость
Fig. 3. Dependence of loaded beam vibrations on given initial parameters: a – horizontal plane;
b – vertical plane
Подбор значения поперечного сечения балки не зависит от характеристик изоляционного материала, а базируется на условиях прочности и таком показателе, как жесткость конструкционного элемента. Но, с другой стороны, дает возможность варьировать значением толщины стенки в сторону уменьшения.
Прогнозируемое сокращение числа значительных циклов для металлических конструкций, демпфируемых с помощью низкомодульных пенопластов, может быть использовано как фундамент для детальной проработки эффективного метода повышения долговечности конструкций.
Сегодня это актуально для строительной техники, эксплуатирующейся в разных отраслях в режимах повышенных динамических нагрузок широкого спектра. Исследование конструкций на примере балок из стали под воздействием постоянно колеблющихся импульсных нагрузок позволило бы глубже выразить теоретическое обоснование.
Вычислительные эксперименты выявили лишь принципиальную возможность продления срока службы деталей машин, демпфируемых наполнителем. Необходимо непосредственно в экспериментах проверять усталостные свойства наполнителя, его адгезию к металлу. Рациональное решение может быть найдено при дополнительном изучении схемы размещения наполнителя внутри конструкции.
С точки зрения задач оптимизации необходимо проводить оценку стоимости проекта. В то же время представленные результаты показали, что такой способ демпфирования имеет хорошие перспективы с точки зрения повышения прочности и долговечности элементов металлических конструкций.
Список литературы
1. <i>Щипачев А.М., Мухин В.С.</i> Модель влияния поверхностного пластического деформирования на усталостную долговечность. Известия высших учебных заведений. Авиационная техника. 2002;(1):76–77.
2. <i>Либерман Я.Л., Летнев К.Ю.</i> Автоматическое устранение колебаний груза на гибкой подвеске при подъеме и опускании. Екатеринбург: УрФУ; 2012.
3. <i> Болотин В.В., Новичков Ю.Н.</i> Механика многослойных конструкций. Москва: Машиностроение; 1980.
4. <i>Смирнов В.И.</i> Курс высшей математики. Т. 2. Москва: Наука; 1974.
5. <i>Алямовский А.А., Собачкин А.А., Одинцов Е.В., Харитонович А.И., Пономарев Н.Б.</i> SolidWorks. Компьютерное моделирование в инженерной практике. Санкт-Петербург: БХВ-Петербург; 2005.
6. <i>Дусье В.Е., Наварский Ю.В., Жегульский В.П.</i> Расчет и проектирование металлических конструкций мостового крана. Екатеринбург: УГТУ-УПИ; 2007.
Об авторе
А. А. СерыхРоссия
Алексей Александрович Серых, директор по строительству
ул. Гайдара, д. 14, г. Хабаровск, 680000, Российская Федерация
e-mail: Kaliberdajob@mail.ru
Рецензия
Для цитирования:
Серых А.А. Способ повышения прочности и долговечности тонкостенных элементов металлических конструкций. Вестник НИЦ «Строительство». 2025;44(1):75-83. https://doi.org/10.37538/2224-9494-2025-1(44)-75-83. EDN: LXCJHG
For citation:
Serykh A.A. Method for increasing the strength and durability of thin-walled elements in metal structures. Bulletin of Science and Research Center of Construction. 2025;44(1):75-83. (In Russ.) https://doi.org/10.37538/2224-9494-2025-1(44)-75-83. EDN: LXCJHG


























