Перейти к:
Развитие метода эффективной расчетной длины в расчетах одноэтажных рам
https://doi.org/10.37538/2224-9494-2025-2(45)-45-67
EDN: PIRRYM
Аннотация
Введение. Настоящие нормы по стальным конструкциям (СП 16.13330.2017) предлагают два метода решения задачи устойчивости рамных конструкций – единые нелинейные системы и метод эффективных расчетных длин. Первый метод не востребован, поэтому метод расчетных длин остается единственным для расчетов. В текущем своде правил содержится ограниченное количество расчетных схем для определения коэффициента расчетной длины, не дающее в полной мере ответы на текущие инженерные запросы, что приводит к трудностям в поиске быстрого ответа и заставляет использовать численный анализ, который хоть и дает достаточно надежные результаты, но требует большего времени на вычисления. В статье предлагается возможный путь развития метода расчетных длин, демонстрируются конкретные примеры решения задач, что поможет не только решить приличное количество типичных случаев одноэтажных зданий, но и предоставить необходимую теорию для решения многоэтажных случаев.
Цель. Развитие метода эффективной расчетной длины.
Материалы и методы. Разработка уравнений коэффициента расчетной длины путем модификации метода сдвига, сравнение полученных аналитических решений в программном комплексе ЛИРА-САПР.
Результаты. Проделанная аналитическая работа предлагает набор уравнений в поддержку развития метода эффективных расчетных длин. Предлагаемые решения дополняют документ СП 16.13330.2017. Результаты численного анализа подтверждают полученные аналитические решения.
Выводы. Возможность расширения свода правил по стальным конструкциям – СП 16.13330.2017.
Ключевые слова
Для цитирования:
Ильюшенков А.О. Развитие метода эффективной расчетной длины в расчетах одноэтажных рам. Вестник НИЦ «Строительство». 2025;45(2):45-67. https://doi.org/10.37538/2224-9494-2025-2(45)-45-67. EDN: PIRRYM
For citation:
Ilyushenkov A.O. Development of the effective length method for single-story frame analysis. Bulletin of Science and Research Center of Construction. 2025;45(2):45-67. (In Russ.) https://doi.org/10.37538/2224-9494-2025-2(45)-45-67. EDN: PIRRYM
Предпосылки
Любому отечественному инженеру известно, что такое эффективная расчетная длина. Прошло более века с того времени, когда профессор Ф. С. Ясинский предложил данное понятие. Согласно его мысли, мы всегда можем найти некоторый эквивалентный по устойчивости шарнирно-закрепленный стержень Эйлера физически реальному стержню с заданным набором опорных связей. Для наглядности интерпретации мысли достаточно посмотреть на рис. 1, на котором показана П-образная рама с заделкой в фундаментах в момент упругой потери устойчивости поперек. Эффективная расчетная длина hef – это расстояние между двумя точками перегиба изогнутой оси стержня.
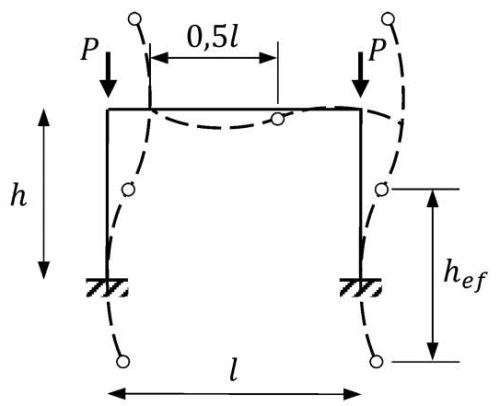
Рис. 1. Геометрическая интерпретация эффективной расчетной длины на примере однопролетной рамы
Fig. 1. Geometric interpretation of effective length using a single-span frame as an example
Согласно [1, п. 4.7.1], эффективные длины следует устанавливать в случаях, когда выполнить расчет конструкций как единых систем по деформированной схеме с учетом пластических деформаций стали не представляется возможным. Допускается принимать приближенные расчетные схемы, которые должны отображать действительные условия нагружения колонн и закрепления их концов; при этом следует учитывать неравномерность распределения вертикальной нагрузки между колоннами, различие жесткостей колонн [1, п. 4.7.6].
Но нормативный подход в основном предлагает нам рассматривать расчетные схемы равнонагруженными, что говорит о возможности расчета при условии потери устойчивости всех колонн одновременно. Первой теряет устойчивость более нагруженная колонна, другие же колонны делают это вынуждено. При этом, конечно же, мы принимаем во внимание и требование по предельной гибкости [2].
Похоже, что раздел единых нелинейных систем [3] в инженерной практике сегодня не используется. Вместе с этим за рубежом [4] растет интерес к прямому анализу (direct analysis). Расчеты по этому методу выполняются по деформированной схеме с включением геометрических и физических несовершенств и μ = 1. Однако такая методика пока что недоступна для отечественного инженера, поэтому метод эффективных длин остается единственным актуальным в нормах способом расчета конструкций на устойчивость. Вместе с тем в стальных конструкциях существует немало задач, решение которых не найти в аналитическом виде. Это мотивирует к тому, чтобы изыскать возможность улучшить метод эффективных длин, дабы разрешить наиболее частые, остро значимые проблемы в определении расчетных длин и представить инженеру более гибкую аналитическую методику расчета.
Для верификации использованы программные комплексы ЛИРА-САПР и ABAQUS. Так как, согласно п. 4.2.5 [2], допускается выполнять проверку устойчивости стержневых конструкций (в том числе пространственных) с использованием сертифицированных вычислительных комплексов как идеализированных систем в предположении упругих деформаций стали.
В связи с объемностью теории в статье рассматриваются только одноэтажные рамы.
Нормативный подход в решении задачи о коэффициенте расчетной длины
Коэффициент расчетной длины определяется из решения приближенного дифференциального уравнения изогнутой оси стержня (1б), полученного путем упрощения точного уравнения (1а):
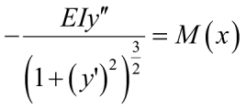 . (1а)
. (1а)
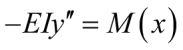 . (1б)
. (1б)
Если рассмотреть деформированное состояние стержня (рис. 2а) под воздействием внешних сил и составить уравнение равновесия изгибающего момента в точке на расстоянии x (рис. 2б):
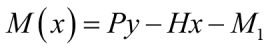 , (2)
, (2)
а затем подставить (2) в (1б), получим неоднородное дифференциальное уравнение (ДУ) сжато-изогнутой оси стержня:
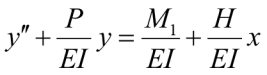 . (3)
. (3)
Решая такое ДУ, приходим к известному трансцендентному уравнению для сжато-изогнутого стержня с тремя упругими опорами (рис. 2в):
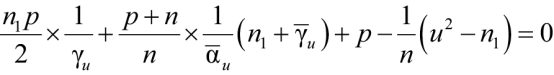 , (4)
, (4)
где
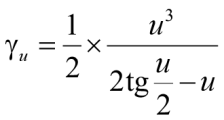 ;
;
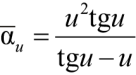 ;
;
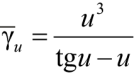 – тригонометрические функции, обладающие общим свойством быть разложенными в ряд в форме неполных квадратичных функций вида
– тригонометрические функции, обладающие общим свойством быть разложенными в ряд в форме неполных квадратичных функций вида
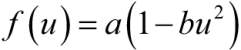 ;
;
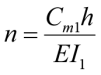 ;
; 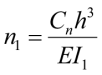 ;
; 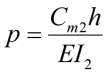 – безразмерные нормативные параметры жесткости угловой и линейной опор (связей);
– безразмерные нормативные параметры жесткости угловой и линейной опор (связей);
Cm – коэффициент жесткости упругого защемления, равный значению реактивного момента, возникающего в опорном сечении при повороте его на угол, равный 1;
Cn – коэффициент жесткости упругой опоры, равный значению реактивной силы, возникающей в опорном сечении при смещении его на 1;
u – критический параметр устойчивости.
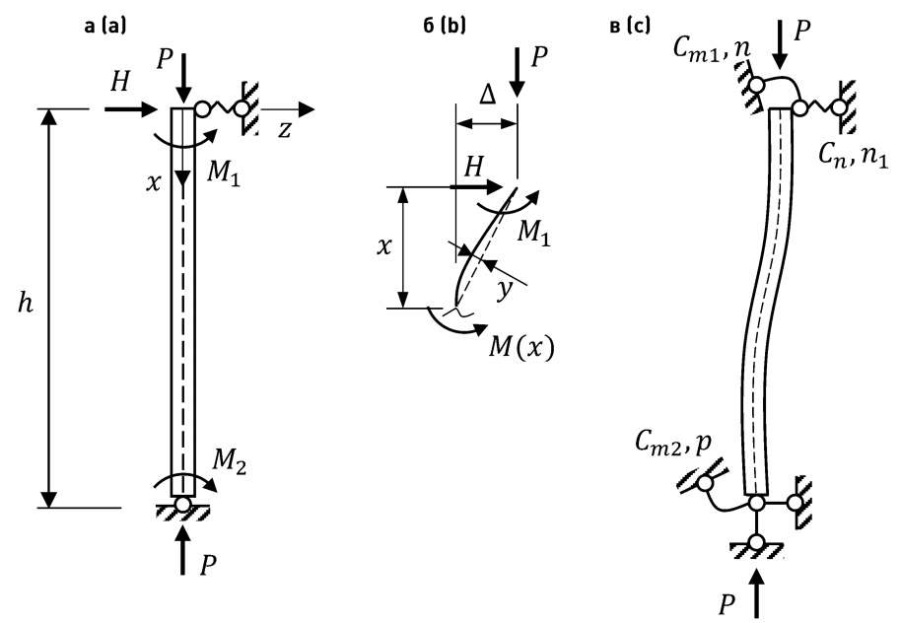
Рис. 2. Шарнирно-закрепленная колонна, подверженная действию сжимающей и моментной нагрузкам
Fig. 2. Pinned column subjected to compressive and moment loads
Критический параметр u можно выразить либо через коэффициент расчетной длины:
 , (5а)
, (5а)
либо через степень нагружения стержня:
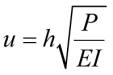 . (5б)
. (5б)
Угловые опоры можно связать при помощи коэффициента ψ:
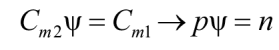 . (6)
. (6)
В самом общем случае рассматривается стержень с тремя упругими опорами, но, исключая из уравнения (4) безразмерные параметры жесткости n, n1, p, приходят к набору частных случаев коэффициентов расчетных длин μ, которые для удобства сведены в таблицы [2, табл. 31] и [3, табл. 24].
Геометрически нелинейный расчет
В геометрически нелинейной постановке задачи уравнения равновесия следует записывать в деформированном состоянии, например (2). Поэтому ДУ (3) позволяет взаимоувязать деформации изгиба и сжатия (деформации сдвига и кручения в расчет не принимаются). Хотя уравнение (3) и линеаризовано, его можно применять до границы умеренно больших перемещений и углов поворота сечений y' = φ < 10°.
Для наглядной демонстрации применимости (3) построена кривая зависимости «φ – u» угла поворота от критического параметра (5б) для сжато-изогнутого консольного стержня (рис. 3). Угол поворота φ подсчитывается по известной формуле (7), полученной из решения ДУ (3) методом прямого интегрирования:
 . (7)
. (7)
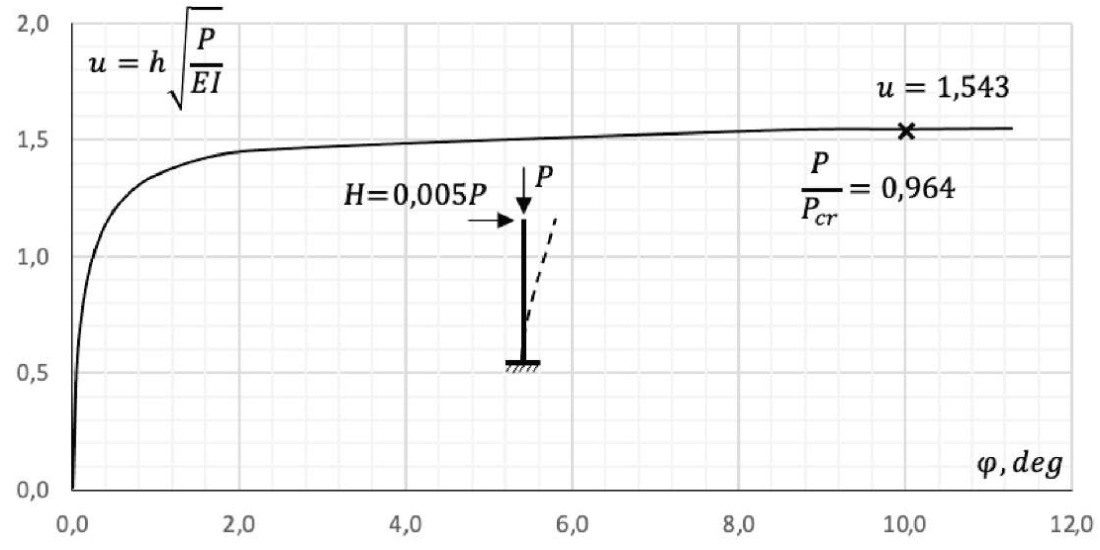
Рис. 3. График зависимости «φ – u» угла поворота от критического параметра устойчивости
Fig. 3. Relationship between rotation angle φ and critical stability parameter u
При уровне нагружения идеально упругого стержня на 96 % результат, полученный через ДУ (3), ничем не отличается от расчета, выполненного в ABAQUS в геометрически нелинейной постановке в предположении бесконечно упругой работы.
То есть мы можем заключить, что квадраты углов поворота элементов φ² = (y')² в точном ДУ (1а) являются величинами того же порядка малости, что и компоненты деформаций. Отсюда и возникает допустимость принятия знаменателя ДУ
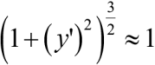
и приведения его к (1б) для стержней, изгибаемых в области умерено больших значений.
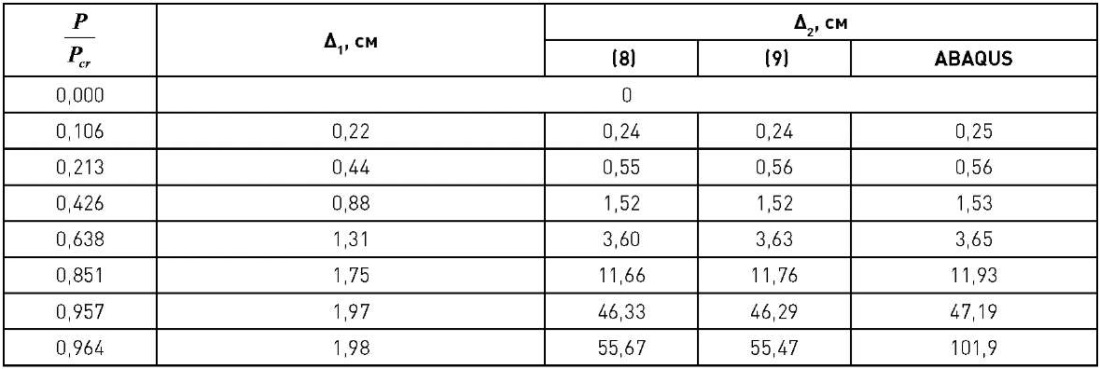
Для сравнения перемещений по результатам расчета поперечного смещения оголовка идеально упругого консольного стержня в процессе нагружения составлена сравнительная табл. 1. Перемещения первого порядка Δ1 без учета влияния функции второго порядка 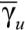 по (8) согласуются только при нагружении стержня до 10 %, то есть в области малых перемещений (или «перемещения в малом»). Перемещения второго порядка Δ2, вычисленные по формулам (8) и (9) через приближенное ДУ (3), полностью согласуются с численным расчетом в ABAQUS вплоть до ~90 %. Далее приближенное уравнение отстает, и с ростом сжимающей силы все больше и больше занижает перемещения. При этом, как известно, при максимуме, то есть u = 0,5π, перемещения в (8) и (9) становятся бесконечными. Соответственно, в области больших перемещений следует применять только точное дифференциальное уравнение изогнутой оси (1а), позволяющее определить конечные «перемещения в большом» и закритическое поведение стержня.
по (8) согласуются только при нагружении стержня до 10 %, то есть в области малых перемещений (или «перемещения в малом»). Перемещения второго порядка Δ2, вычисленные по формулам (8) и (9) через приближенное ДУ (3), полностью согласуются с численным расчетом в ABAQUS вплоть до ~90 %. Далее приближенное уравнение отстает, и с ростом сжимающей силы все больше и больше занижает перемещения. При этом, как известно, при максимуме, то есть u = 0,5π, перемещения в (8) и (9) становятся бесконечными. Соответственно, в области больших перемещений следует применять только точное дифференциальное уравнение изогнутой оси (1а), позволяющее определить конечные «перемещения в большом» и закритическое поведение стержня.
Таблица 1
Сравнительная таблица перемещений первого и второго порядков
Table 1
Comparative analysis of first- and second-order displacements
В реализации учета геометрически нелинейных эффектов важен также порядок приложения нагрузок. Принцип суперпозиции здесь не работает: A + B ≠ B + A.
При рассмотрении задачи через ДУ вида (3) перемещения второго порядка Δ2 увязаны с перемещениями первого порядка Δ1 при помощи специальных тригонометрических функций из уравнения (4). Например для рассматриваемого консольного стержня (рис. 3), уравнение перемещение Δ2 верха имеет вид:
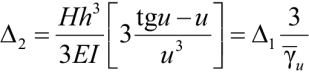 , (8)
, (8)
где Δ1 – перемещения первого порядка только от действия горизонтальной силы H;
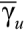 – нелинейная функция второго порядка, увязывающая сжимающую силу и перемещения.
– нелинейная функция второго порядка, увязывающая сжимающую силу и перемещения.
Аппроксимация тригонометрической функции 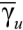 в (8) в границах 0 ≤ u ≤ 0,5 π:
в (8) в границах 0 ≤ u ≤ 0,5 π:
 . (9)
. (9)
Если критический параметр u заменить (5б), то получим обобщенное выражение, связывающее перемещения первого и второго порядков через коэффициент расчетной длины μ:
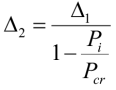 , (10)
, (10)
где Pi – осевая сжимающая сила, действующая в рассматриваемом i-м стержне;
Pcr – упругая критическая сила i-го стержня, которая может быть приведена к силе Эйлера шарнирно-закрепленного стержня через коэффициент расчетной длины Pe = μ²Pcr.
Другой способ рассмотрения геометрически нелинейной задачи – прямое суммирование перемещений первого порядка и перемещений, возникающих при расчете по деформированной схеме. А именно: отклонение стержня от вертикальности (P – Δ эффект); отклонение стержня от прямолинейности (P – δ эффект). P – Δ эффект определяет глобальное отклонение системы, а P – δ эффект распространяется на отдельно выбранный стержень, находящийся под действием сжимающей силы Pi.
Суммарные перемещения второго порядка:
Δ2 = ΔH + ΔP – Δ + ΔP – δ. (11)
Горизонтальная сила H (рис. 4) является действительной и создает действительную работу внешних сил, так как она совершается на перемещениях, вызванных этой же силой. Сила H позволяет создать отклоненную, но не конечную форму деформаций. И перемещения ΔH = Δ1 только от H меньше Δ2. Вертикальная сила P совершает возможную работу на перемещениях по их направлению и вызвана силой H. При этом силы, совершающие возможную работу, должны предварительно достичь своего окончательного значения. Это объясняет принцип P – Δ анализа и расчетов по деформированной схеме.
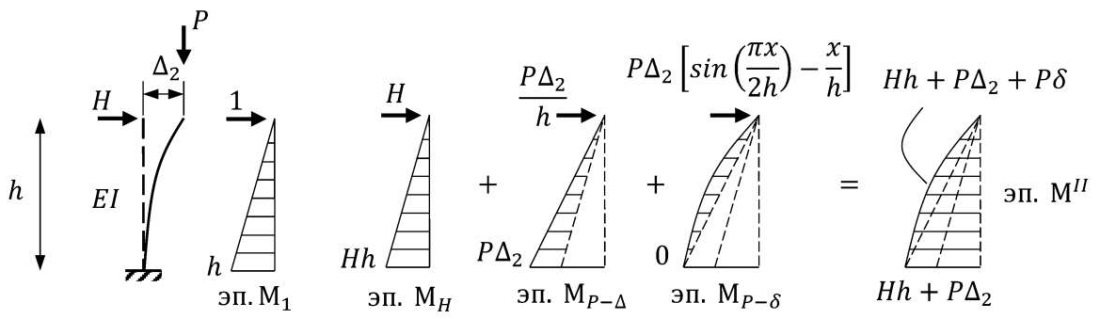
Рис. 4. Эпюры изгибающих моментов по деформированной схеме
Fig. 4. Bending moment diagrams along the deformed shape
Перемещения ΔP – Δ и ΔP – δ можно вычислить, например, методом сил. Для этого достаточно построить единичную эпюру M1 и поочередно перемножить с эпюрами MP – Δ и MP – δ, как это показано на рис. 4. Опуская математические детали решения, приведем сразу полное уравнение перемещений Δ2 для консольного стержня:
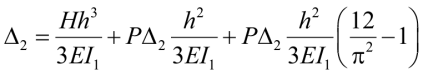 . (12)
. (12)
Из равенства (12) выражаем перемещение второго порядка:
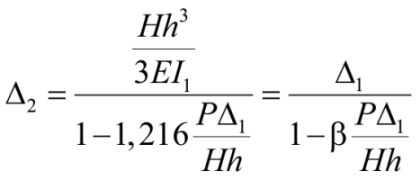 . (13)
. (13)
Уравнение (13) по виду повторяет (10). Числовой коэффициент β варьируется в разных случаях закреплений стержня по концам. Он определяет сжато-изогнутое состояние стержня или P – δ эффект. Очевидное следует из построенной эпюры MP – δ на рис. 4.
Также следует учитывать, что перемещения могут определяться для цепочки или ряда связанных друг с другом стержней в одном уровне, когда речь идет о поперечном смещении (сдвиге) целого этажа или покрытия, а не только изолированного стержня. Поэтому в общем случае в уравнении (13) силу P следует заменить на сумму сил ΣP:
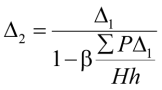 . (14)
. (14)
Метод сдвига
В 1977 году ЛеМессурье в работе [5] предложил практический метод расчета строительных конструкций на устойчивость по деформированной схеме, известный сегодня как метод жесткости или сдвига (ориг. Story stiffness approach) [4]. Приравнивая формулы (10) и (14), полученные из геометрически нелинейного анализа, мы приходим к обобщенному уравнению коэффициента расчетной длины методом сдвига:
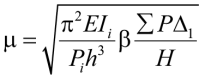 . (15)
. (15)
Данный метод может считаться эффективным в расчетах на устойчивость многопролетных одно- и многоэтажных рам. Он удобен в использовании при непосредственном участии вычислительных комплексов, когда перемещения или сдвиг выбранного этажа Δ1 вычисляются численным способом, а ΣP, Pi и H выбираются из соответствующей комбинации усилий. Вместе с этим метод по-своему непрост в интерпретации. Коэффициент β весьма труден для точной калькуляции даже для самых простых конструктивных схем. И у данного метода по сути никогда не было аналитического аппарата, позволяющего вычислить коэффициент расчетной длины без применения вычислительных комплексов.
Модификация уравнения
Однако существует вполне четкая видимость в улучшении интерпретации метода сдвига. Работа над модификацией уравнения (15) может представить дополнительные возможности, позволит серьезным образом расширить технику расчетов коэффициента расчетной длины согласно [2][3], при этом не нарушая его целостности.
По названию метода можно заметить, что в уравнении (15) присутствует коэффициент жесткости упругой опоры Cn, определяющий смещение или сдвиг выбранного этажа. Для одноэтажной рамы это обычно смещение поперек в уровне покрытия:
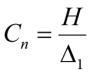 . (16)
. (16)
Поперечная жесткость, которую способна создать рама, может быть вычислена от единичной силы H = 1. При этом любое единичное перемещение для любой рамы может быть определено через следующее обобщенное уравнение:
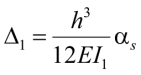 , (17)
, (17)
где αs – это обобщенный коэффициент жесткости рамы, который зависит от n и p;
EI1 – изгибная жесткость колонны, относительно которой выражается перемещение Δ1.
Подставляем (17) в (15):
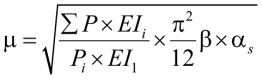 . (18)
. (18)
Сейчас отчетливо видно, что коэффициент расчетной длины (18) может быть разбит на три понятных множителя.
Первый множитель обозначим через μef:
 , (19)
, (19)
где ΣP – суммарная действующая сила в уровне выбранного этажа;
Pi и EIi – сжимающая сила и изгибная жесткость i-й колонны, для которой вычисляется коэффициент расчетной длины;
EI1 – изгибная жесткость колонны, относительно которой было определено смещение этажа.
Коэффициент μef выполняет часть условий [1, п. 4.7.6]. Он учитывает различия жесткостей колонн, действительные условия нагружения колонн и неравномерность распределения вертикальной нагрузки между колоннами.
Если считается, что колонны нагружены одинаковой сжимающей силой по своду правил [2], то следует очевидный вывод:
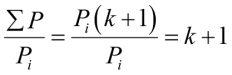 , (20)
, (20)
где k – количество пролетов, при k = 1, μef = 1, при k = 2, μef = 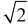 и т. д.
и т. д.
Второй множитель обозначим через η:
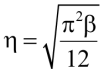 . (21)
. (21)
Коэффициент η учитывает закрепления концов колонны и влияние P – δ согласно [1, п. 4.7.6]. Для простоты понимания коэффициент η можно истолковать как коэффициент, зависящий от формы потери устойчивости колонны. Форма потери устойчивости в свою очередь зависит от вида закреплений стержня на концах. Поэтому для консольного стержня максимальный случай βmax = 1,216, при котором η = 1. Для рамного стержня это не так. Любой стержень многоэтажной рамы обычно имеет две упругие опоры защемления, поэтому форма потери устойчивости таких колонн чаще выражается в виде двух антисимметричных полуволн. В свою очередь колонны первого этажа сопряжены либо шарнирно, либо имеют заделку в фундаментах, но все равно имеют одну упругую опору защемления. Подход с βmax и η = 1 часто применяется для упрощения решения одноэтажных рам. В связи с этим коэффициент расчетной длины немногим будет завышен. Н. В. Корноухов [6] в свое время распознавал коэффициент β как некоторый поправочный коэффициент, устанавливающий взаимосвязь между углами касательной, хорды и поворотов колонны для повышения точности расчетов. И для стержня многоэтажной рамы с одинаковой жесткостью примыкающих ригелей пришел к абсолютно такому же выражению, как и ЛеМессурье. Н. В. Корноухов останавливается на среднем значении коэффициента βavg = 1,1, указывая, что даже грубые формулы при значении β = 1,1 дают достаточную точность. С этим утверждением нельзя не согласиться. Детальная работа над коэффициентом β и его аналитические формулировки были рассмотрены в работе [7]. Здесь же ограничимся только выводами и формулами для расчетов.
Для всех рамных систем, включая одноэтажные рамы с шарнирным прикреплением колонн к фундаментам (включая рамы переменного сечения), рекомендуется следующая линейная зависимость:
β = 1 + 0,1n ≤ 1,216. (22)
Для одноэтажных рам в запас возможно принимать βmax = 1,216 и η = 1. Для регулярных одно- и многоэтажных многопролетных рам, рассчитываемых в упругой области, безопасно принимать усредненное значение βavg = 1,1 и ηavg = 0,95. Данные значения подтверждаются результатами исследований и расчетами на устойчивость. Исключение составляет рама с заделкой баз колонн в фундаментах. Рекомендуется принимать осредненное значение ηavg = 0,97. Применять формулу (22) для это случая не рекомендуется, так как необъективно создается занижение расчетной длины колонны.
Используя введенные сокращенные обозначения (19) и (21), коэффициент расчетной длины может быть представлен в новом виде:
μ = μef × η × 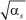 . (23)
. (23)
Коэффициент αs может быть получен методами строительной механики. Он достаточно хорошо известен в расчетах, в том числе и на сейсмическое воздействие, и представляет собой обыкновенную функцию αs(n,p).
Согласно общепринятому подходу, многоэтажные рамы делят на простые равноустойчивые этажи-ячейки (рис. 5) [6]. В выделяемой ячейке колонны имеют одинаковую изгибную жесткость EI1, а примыкающие к ним сверху и снизу ригели имеют разные изгибные жесткости EI2 и EI3. При этом жесткость ригелей между этажами обычно делится пополам.
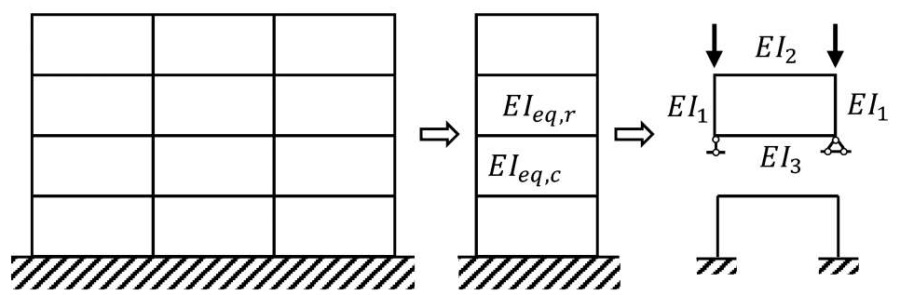
Рис. 5. Принцип деления многоэтажной рамы на простые равноустойчивые ячейки
Fig. 5. Principle of dividing a multi-story frame into simple equally stable cells
В самом общем случае сдвиг контурной рамы от единичной горизонтально приложенной силы:
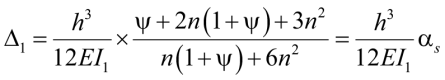 , (24)
, (24)
где
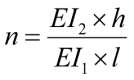 ;
;
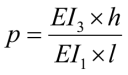 ;
;
n = pψ – безразмерные погонные жесткости контурной рамы по [2];
EI2, EI3 – изгибные жесткости ригелей, примыкающие сверху и снизу соответственно.
Другие (частные) случаи получаются путем изменения параметров n, p и ψ.
Например, если жесткости ригелей равны p = n или ψ = 1, тогда:
 . (25)
. (25)
Аналогичным образом составляются и другие коэффициенты αs. Можно использовать готовые формулы с эпюрами моментов для последующего нахождения поперечного смещения рамы, например по книге Д. В. Бычкова [8]. Для удобства составлена табл. 2 коэффициентов жесткости рамы αs и коэффициентов расчетных длин μ для элементарных случаев по формулам (23) и (24) при η = 1.
По величине αs можно также установить тип смещения рамы поперек. При более высоких значениях n и p коэффициент αs будет стремиться к минимальному значению. Такую раму следует относить к конструкции, работающей преимущественно по сдвиговому механизму (недеформируемый ригель). При более низких значениях n и p коэффициент αs приближается к максимуму, а рассматриваемая рама относится к изгибаемому типу (ригель имеет крайне низкую изгибную жесткость либо шарнирное примыкание n < 0,1). Колонны многоэтажных каркасов в таких случаях работают преимущественно как свободные консольные стержни. В более общих и практически реализуемых случаях коэффициент αs оказывается между двумя крайними значениями как функция отношения погонных жесткостей балки и колонны αs = f(n, p). Работа каркаса происходит по изгибно-сдвиговому механизму и может меняться от этажа к этажу.
Таблица 2
Таблица коэффициентов αs и μ для элементарных рам
Table 2
Table of 2 αs and μ factors for elementary frames
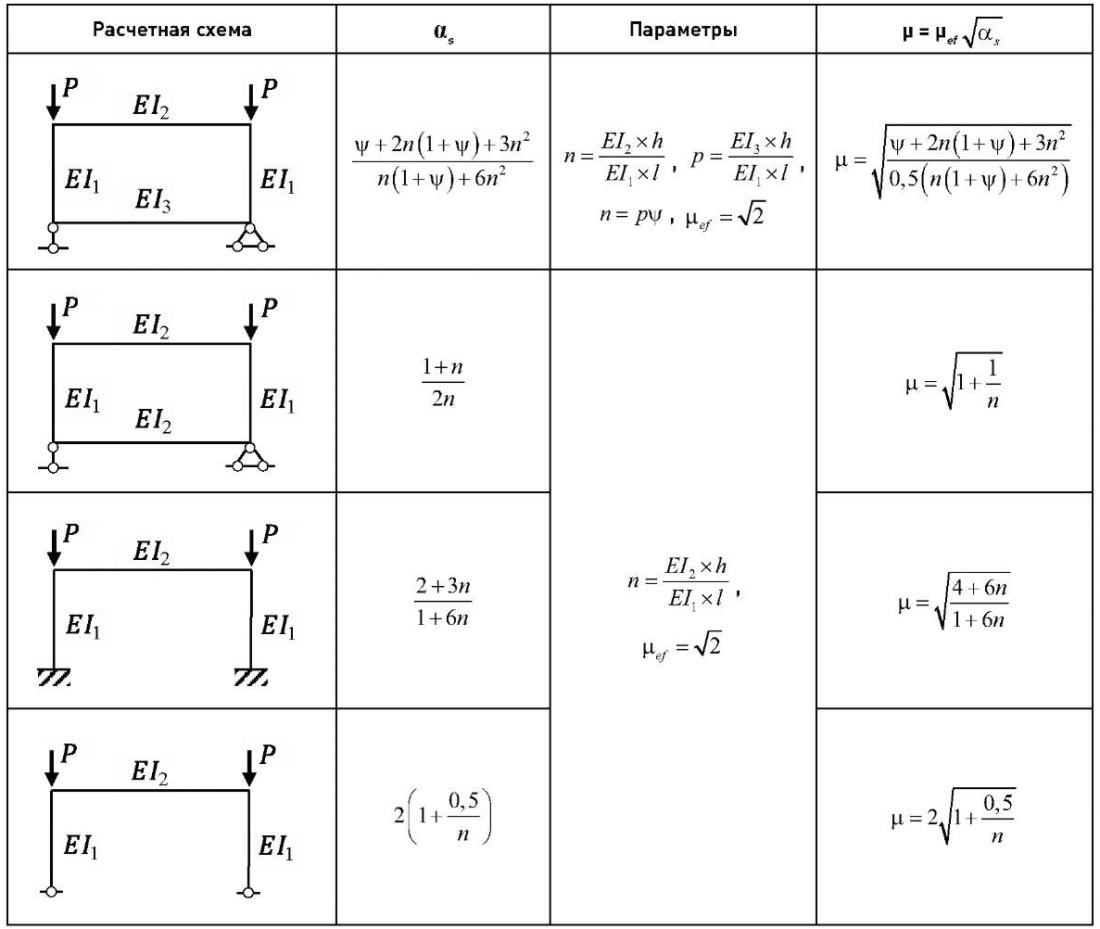

Обозначения, принятые в табл. 2:
I2, I3 – моменты инерции сечения ригелей, примыкающих соответственно к верхнему и нижнему концу проверяемой колонны;
I1 – момент инерции колонны;
h – высота колонны;
l – пролет рамы;
μef – коэффициент перераспределения жесткости и нагрузки;
αs – коэффициент жесткости рамы.
Примеры решения задач устойчивости
На основании изложенной теории рассмотрим несколько практических случаев, позволяющих оценить возможности метода сдвига и формулы (23) в создании универсальных аналитических решений для одноэтажных рам.
1. Исследуем двухпролетную раму, показанную на рис. 6а. В результате реконструкции к П-образной раме была пристроена Г-образная рама. Требуется определить μ для каждой из колонн. Исходные данные для расчета: колонны П-образной рамы 20К1, EI1 = 7923 кНм², ригель 40Б1, EI2 = 41 239 кНм². Колонна пристройки 25К1, EI3 = 18 892 кНм², ригель 45Б1, EI4 = 59 117 кНм². Размеры рамы: h = 6 м, l1 = 15 м, l2 = 10 м. P1 = 90 кН, P2 = 140 кН, P3 = 65 кН. ΣP = 295 кН, ηavg = 0,95.
Поперечная жесткость, которую способна создать двухпролетная рама (рис. 6а), состоит из суммы поперечных жесткостей П-образной (рис. 6б) и Г-образной (рис. 6в) рам свободно смещаться поперек:
Cn = Cn,1 + Cn,2 (26)
или в перемещениях:
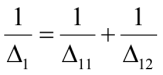 . (27)
. (27)
Из (27) находим приведенное поперечное смещение Δ1 целой конструкции:
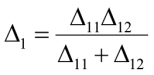 ,
,
где
 – поперечное смещение П-образной рамы по табл. 2 (рис. 6б);
– поперечное смещение П-образной рамы по табл. 2 (рис. 6б);
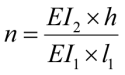 ;
;
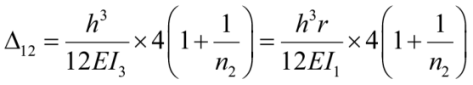 – поперечное смещение Г-образной рамы по табл. 2 (рис. 6в);
– поперечное смещение Г-образной рамы по табл. 2 (рис. 6в);
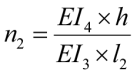 ;
;
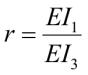 .
.
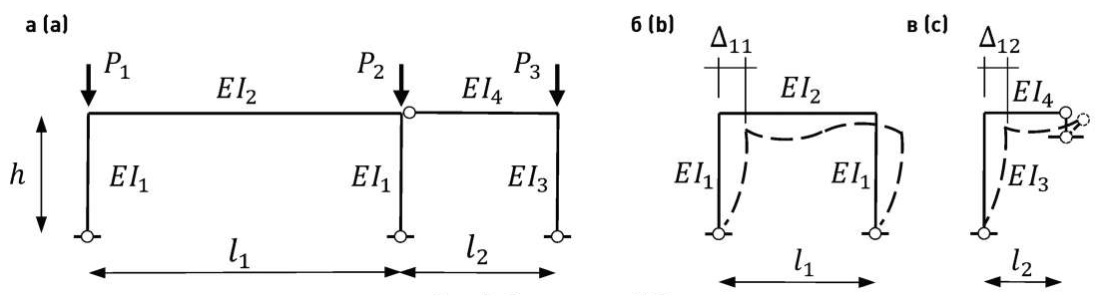
Рис. 6. Схема рамы № 1
Fig. 6. Scheme of frame No. 1
Коэффициент жесткости рамы, показанной на рис. 6, по формуле (27) и подстановке аналитических выражений Δ11 и Δ12:
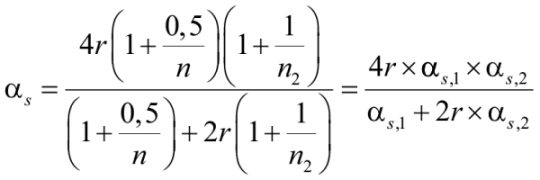 . (28)
. (28)
Подсчитываем характеристики рамы:
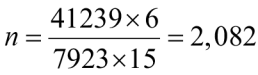 ,
,
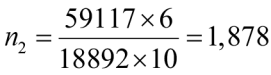 ,
,
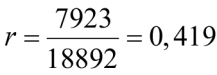 ,
,
αs1 = 1,240, αs2 = 1,532.
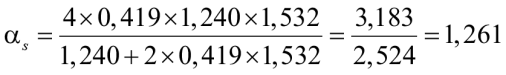 .
.
Коэффициенты перераспределения μef,i:
Для левой колонны
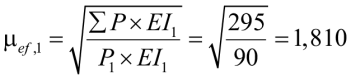 .
.
Центральная колонна
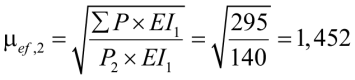 .
.
Правая колонна
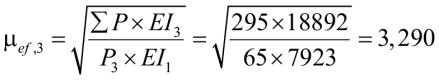 .
.
По формуле (23) вычисляем коэффициенты расчетных длин. Результаты сводим в табл. 3, куда также заносим результаты проверки, сделанные в ЛИРА-САПР, а также расчеты в предположении равномерного нагружения колонн P1 = P2 = P3. Таким же образом можно решить раму со смешанным прикреплением к фундаментам, используя табл. 2.
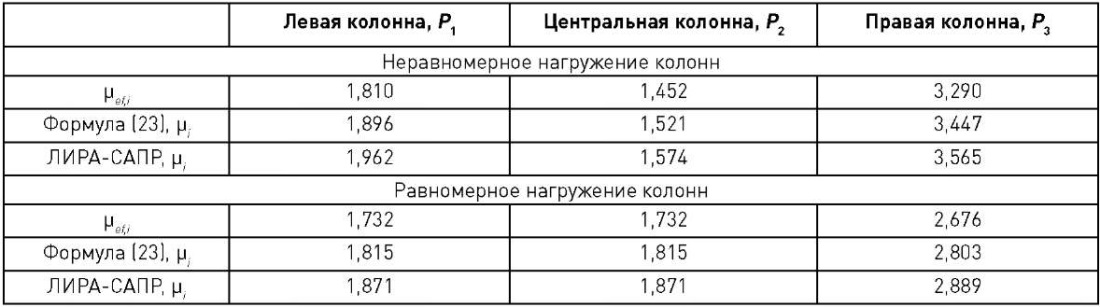
Таблица 3
Сравнительная таблица результатов аналитического и численного решений
Table 3
Comparison of analytical and numerical solution results
2. В качестве следующего примера рассмотрим одноэтажную k-пролетную раму (рис. 7а). Задача – создать обобщенную аналитическую формулу для быстрой калькуляции коэффициента расчетной длины μi любой колонны.
За эквивалентную систему принимаем Г-образную раму с половиной пролета (рис. 7б).
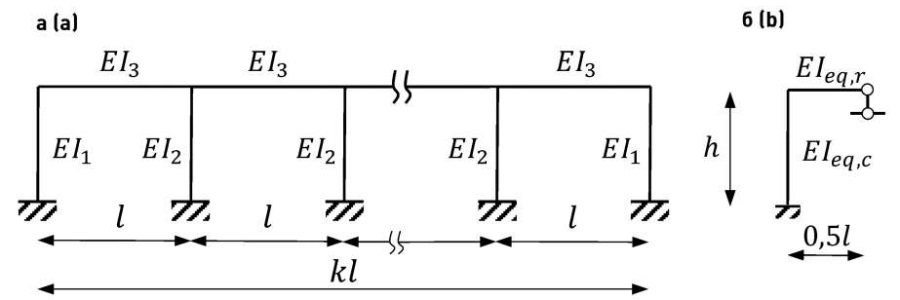
Рис. 7. Схема рамы № 2
Fig. 7. Scheme of frame No. 2
Эквивалентная изгибная жесткость ригеля складывается из суммы половин пролетов и изгибных жесткостей ригеля:
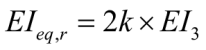 . (29)
. (29)
Эквивалентная изгибная жесткость колонны складывается из суммы крайних (которых всегда две) и рядовых колонн:
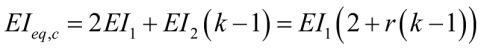 , (30)
, (30)
где
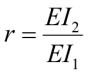 – параметр отношения жесткости колонн;
– параметр отношения жесткости колонн;
k – число пролетов.
Эквивалентный параметр жесткости рамы neq при k одинаковых пролетах с учетом (29) и (30):
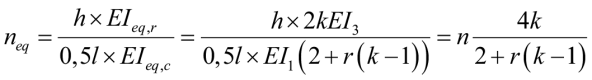 , (31)
, (31)
где
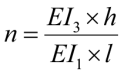 – нормативный безразмерный параметр жесткости.
– нормативный безразмерный параметр жесткости.
Единичное перемещение Г-образной рамы с жестким прикреплением к фундаменту от единичной горизонтальной силы, приложенной в рамном узле по табл. 2:
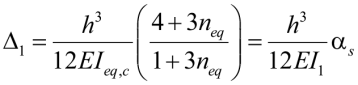 , (32)
, (32)
где
 с учетом подстановки (30) и (31).
с учетом подстановки (30) и (31).
Для случая, если рама имеет шарнирное сопряжение с фундаментами, следует использовать другое выражение и коэффициент αs:
 , (33)
, (33)
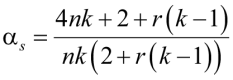 .
.
Суммарная сила, когда колонны нагружены неравномерно:
 . (34)
. (34)
Пусть жесткость крайних колонн EI1 = 4002 кНм², жесткость рядовых колонн EI2 = 7286 кНм² и изгибная жесткость ригелей EI3 = 7286 кНм². Сжимающие силы: крайняя колонна P1 = 10 кН, рядовая колонна P2 = 30 кН. Размеры рамы: h = 6 м, l = 15 м. ηavg = 0,97.
Вычисляем характеристики рамы:
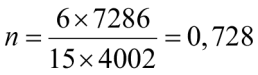 ,
,
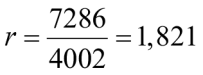 .
.
Создадим сравнительную табл. 4. Посчитаем раму с защемлением в фундаментах по рис. 7а с числом пролетов до k = 8 и сравним значения μ по (23) и ЛИРА-САПР.
Таблица 4
Сравнительная таблица результатов аналитического и численного решений
Table 4
Comparison of analytical and numerical solution results
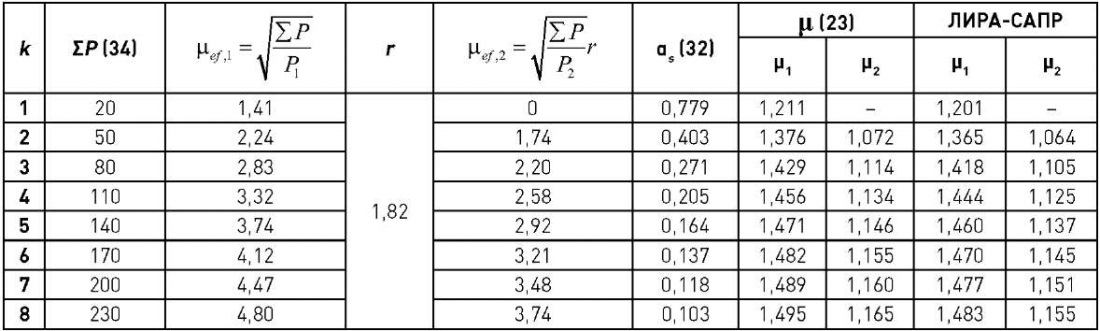
Между коэффициентами расчетных длин μ1 и μ2 существует взаимосвязь. Если приравнять выражения коэффициентов расчетных длин μ1 и μ2 через сумму сил ΣP, то будет получено равенство:
 . (35)
. (35)
3. Следующим примером разберем один из частых случаев в расчетах на устойчивость. Задача – создать универсальное уравнение коэффициента расчетной длины при любой комбинации сил и длинах колонн. Две консольные колонны шарнирно соединены балкой (или фермой), которая загружена силой P. Сила P находится не на середине пролета, что имитирует комбинацию с неравномерным распределением нагрузки в пролете. Расчетная схема показана на рис. 8а.
Деление сжимающей силы между колоннами на P1 и P2 (рис. 8б) принимается на основании линейного закона:
P1 = (1 – a)P и P2 = aP. (36)
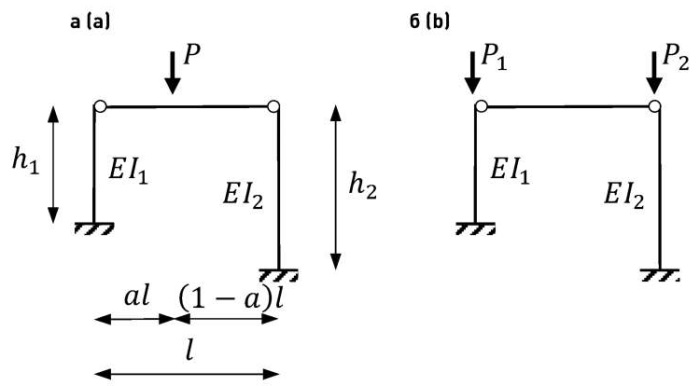
Рис. 8. Схема рамы № 3
Fig. 8. Scheme of frame No. 3
Коэффициент расчетной длины для такого случая не будет μ1 = μ2 = 2. Как и перемещения оголовков колонн, при приложении единичной горизонтальной силы не будут равны своему консольному значению. Очевидно, что перед нами один раз статически неопределимая система (рис. 9), предварительно требующая раскрытия неопределимости.
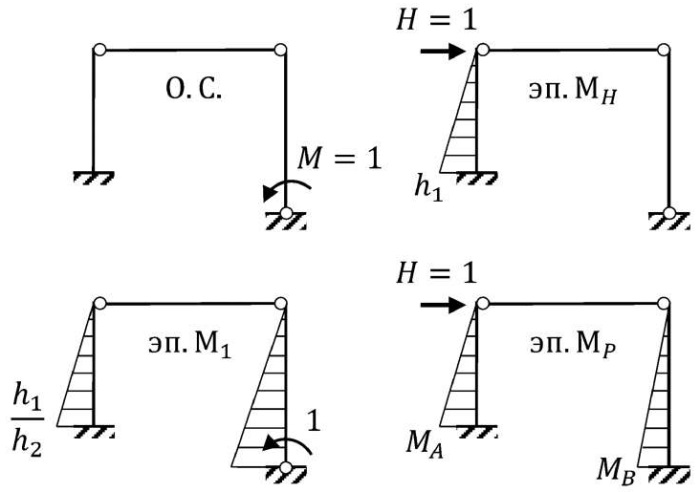
Рис. 9. Эпюры изгибающих моментов
Fig. 9. Bending moment diagrams
Изгибающие моменты в расчетной системе при действии горизонтально действующей силы H = 1, найденные методом сил:
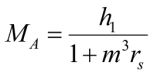 ,
,
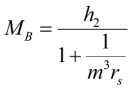 , (37)
, (37)
где
 ;
;
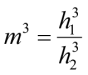 .
.
Перемещение статически неопределимой системы получим путем перемножения расчетной Mp и единичной эпюр M1 методом Верещагина (рис. 9):
 . (38)
. (38)
Из формул (37) и (38) становится вполне очевидно, что взаимосвязь значительно сложнее, чем можно подумать. Соответственно, можно уже сказать, что μ = 2 – это всего лишь частный случай.
Далее (38) подставляем в уравнение коэффициента расчетной длины (23):
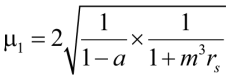 , (39)
, (39)
 . (40)
. (40)
Либо составляя пропорцию, как и для (35), при которой коэффициенты расчетных длин будут выражены как:
 . (41)
. (41)
Если же сила приложена на левой опоре, то есть a = 0, тогда уравнение (39) обратится в:
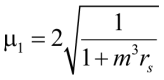 . (42)
. (42)
При m³rs = 3 μ1 = 1. Если m³rs ≈ 1, то имеем тривиальный случай, при котором μ1 = 1,414. Если же m³rs ≈ 0, система обращается в консольный случай. Такое возможно, если жесткость EI2 чрезвычайно мала либо высота левой колонны значительно больше правой h1 ≫ h2. Задачу можно решить и методом приведенной жесткости по (26), в том числе и для n-го количества стержней. Данный подход полезен при рассмотрении эстакад, галерей и объектов реконструкции с присоединением новых элементов.
Согласно [3, табл. 24] и уравнению (4), приведена частная схема (рис. 10а), когда Cm = 0, но Cn ≠ 0.
Для этой схемы коэффициент расчетной длины μ1 подсчитывается по следующей формуле:
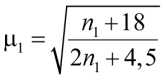 ,
,
2 ≥ μ1 ≥ 0,7, (43)
где
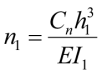 ,
,
Cn – коэффициент жесткости упругой опоры, равный значению реактивной силы, возникающей в опорном сечении при смещении его на 1.

Рис. 10. Схема рамы № 4
Fig. 10. Scheme of frame No. 4
Согласно [3, табл. 25], для рассматриваемого случая:
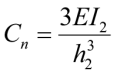 . (44)
. (44)
Подставляем (44) в n1:
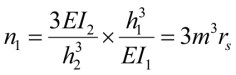 .
.
Затем (44) в коэффициент расчетной длины (43):
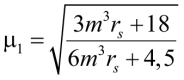 . (45)
. (45)
Получили по виду аналогичное уравнению (42). При m³rs ≈ 4,5 μ1 = 1. Если то m³rs ≈ 0, то μ1 = 2. Если m³rs ≈ 1, то μ1 = 1,414.
Сравним полученные формулы (42) и (45) с расчетом в ЛИРА-САПР. Для этого составим табл. 5. Будем варьировать отношение 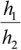 , а EI2 = EI1. Результаты по трем вариантам расчета согласуются друг с другом. При этом нормативное уравнение (45) будет стремиться к минимуму, μ = 0,7 при росте n1. А решение (42), как и численный расчет, при росте n1 будет стремиться к нулю.
, а EI2 = EI1. Результаты по трем вариантам расчета согласуются друг с другом. При этом нормативное уравнение (45) будет стремиться к минимуму, μ = 0,7 при росте n1. А решение (42), как и численный расчет, при росте n1 будет стремиться к нулю.
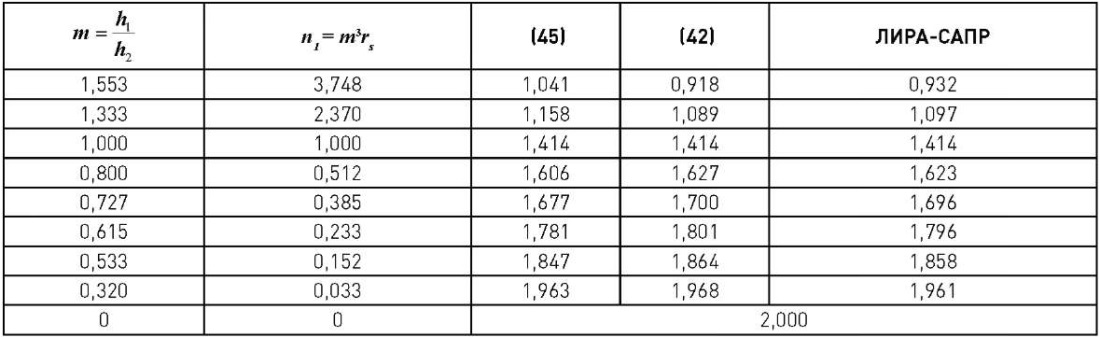
Таблица 5
Сравнительная таблица результатов аналитического и численного решений
Table 5
Comparison of analytical and numerical solution results
Заключение
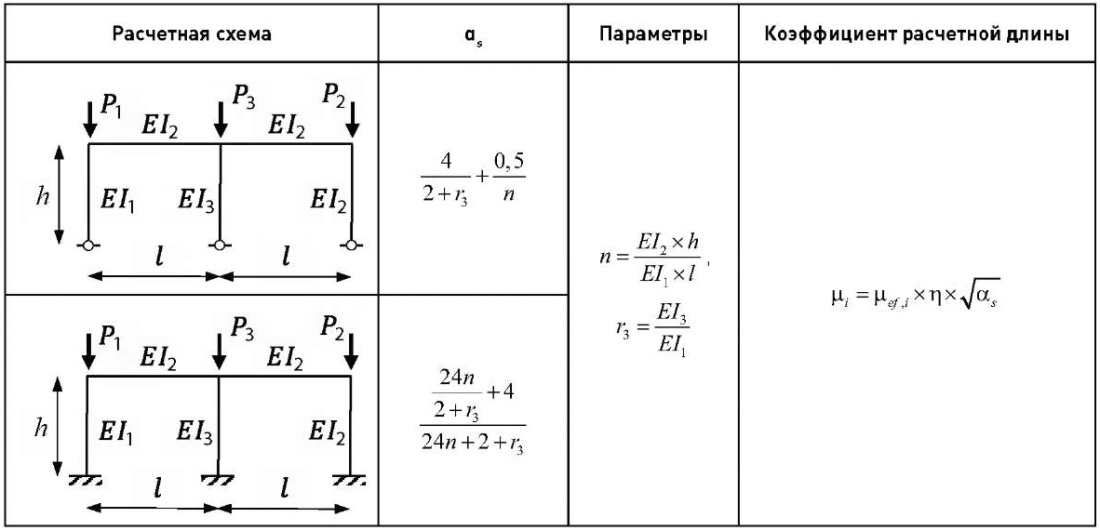
Продемонстрированная методика расчета может быть распространена на множество других задач, в том числе и на любого вида многоэтажные рамы, рамы переменного сечения, системы с колоннами, теряющими устойчивость вынуждено, и т. д. Метод весьма гибок и представляет возможность создать дополнительный набор уравнений μ, не противоречащий своду правил [2]. В качестве такого примера в дополнительной табл. 6 приведены две частные формулы для наиболее часто встречаемого случая двухпролетных рам.
Таблица 6
Дополнительная таблица коэффициентов αs и μ для элементарных рам
Table 6
Supplementary table of coefficients αs and μ for elementary frames
Список литературы
1. СТ СЭВ 3972-83. Надежность строительных конструкций и оснований. Конструкции стальные. Москва: Издательство стандартов; 1985.
2. СП 16.13330.2017. Стальные конструкции. Актуализированная редакция СНиП II-23-81*. Москва: Минстрой России; 2017.
3. СП 294.1325800.2017. Конструкции стальные. Правила проектирования. Москва: Минстрой России; 2017.
4. ANSI/AISC 360-22. Specification for Structural Steel Buildings [internet]. American Institute of Steel Construction; 2022. Available at: https://www.aisc.org/globalassets/product-files-not-searched/publications/standards/a360-22w.pdf.
5. <i>LeMessurier W.J.</i> Practical method of second order analysis. Part 2; Rigid frames. Engineering journal. 1977;14(2):49–67. https://doi.org/10.62913/engj.v14i2.292.
6. <i>Корноухов Н.В.</i> Прочность и устойчивость стержневых систем. Москва: Стройиздат; 1949.
7. <i>Ильюшенков А.О.</i> Устойчивость стальных строительных конструкций. Москва: АСВ; 2023.
8. <i>Бычков Д.В.</i> Формулы и графики для расчета рам. Москва: Госиздат; 1957.
Об авторе
А. О. ИльюшенковРоссия
Александр Олегович Ильюшенков, инженер промышленного и гражданского строительства, АО «Территориальный проектный институт «Хабаровскпромпроект», Хабаровск
ул. Уссурийский бульвар, д. 2, г. Хабаровск, 680000, Российская Федерация
e-mail: revivaltree@gmail.com
Рецензия
Для цитирования:
Ильюшенков А.О. Развитие метода эффективной расчетной длины в расчетах одноэтажных рам. Вестник НИЦ «Строительство». 2025;45(2):45-67. https://doi.org/10.37538/2224-9494-2025-2(45)-45-67. EDN: PIRRYM
For citation:
Ilyushenkov A.O. Development of the effective length method for single-story frame analysis. Bulletin of Science and Research Center of Construction. 2025;45(2):45-67. (In Russ.) https://doi.org/10.37538/2224-9494-2025-2(45)-45-67. EDN: PIRRYM


























