Перейти к:
Особенности методики расчета по прочности наклонных сечений железобетонных конструкций на действие поперечных и продольных сил по СП 63.13330.2018
https://doi.org/10.37538/2224-9494-2025-4(47)-19-32
EDN: GODWIA
Аннотация
Введение. В статье рассмотрена методика расчета наклонных сечений на действие поперечных сил с учетом влияния сжимающих продольных сил, приведенная в СП 63.13330.2018. Были проанализированы точный и упрощенные методы определения средних напряжений, а также методика расчета коэффициента, учитывающего влияние продольных сил на прочность наклонных сечений. Также выполнен сравнительный анализ значений данного коэффициента при определении напряжений по упрощенным и точной методикам, показаны отдельные недостатки нормативной методики в области высоких сжимающих напряжений, которые указывают на необходимость проведения дальнейших исследований.
Цель. Рассмотрение особенностей нормативной методики расчета прочности наклонных сечений железобетонных элементов при действии поперечных и продольных сил.
Материалы и методы. Теоретические исследования проведены на основе результатов численного анализа методик расчетов прочности наклонных сечений, изложенных в СП 63.13330.2018.
Результаты. В работе были выполнены численные теоретические исследования по сравнительному анализу методик расчетов, приведенных в нормах, при различном содержании арматуры в железобетонных элементах. По результатам анализа установлено, что при высоких уровнях напряжения, а также высоком содержании арматуры методики норм могут показывать существенные расхождения, что оказывает влияние на корректность оценки прочности наклонных сечений при действии продольных сил. В связи с этим указывается на необходимость проведения исследований по данному вопросу, включая элементы из высокопрочных бетонов.
Выводы. Анализ нормативных методов расчета прочности наклонных сечений с учетом влияния продольных сил показывает, что при высоком уровне обжатия в ряде случаев могут наблюдаться существенные расхождения в оценке прочности наклонных сечений. Учитывая возможность хрупкого разрушения при действии поперечных сил, это показывает необходимость проведения дальнейших исследований данного вопроса, включая конструкции из высокопрочных бетонов, и дальнейшего развития методики расчета наклонных сечений с учетом продольных сил.
Ключевые слова
Для цитирования:
Зенин С.А., Мухамедиев Т.А., Семенов А.А. Особенности методики расчета по прочности наклонных сечений железобетонных конструкций на действие поперечных и продольных сил по СП 63.13330.2018. Вестник НИЦ «Строительство». 2025;47(4):19-32. https://doi.org/10.37538/2224-9494-2025-4(47)-19-32. EDN: GODWIA
For citation:
Zenin S.A., Mukhamediev T.A., Semenov A.A. Features of calculating the strength of inclined sections for reinforced concrete structures under transverse and longitudinal forces according to SP 63.13330.2018. Bulletin of Science and Research Center of Construction. 2025;47(4):19-32. (In Russ.) https://doi.org/10.37538/2224-9494-2025-4(47)-19-32. EDN: GODWIA
Введение
Как известно, методика расчета наклонного сечения по прочности на совместное действие поперечных и сжимающих сил была откорректирована изменением № 1 к СП 63.13330.2018 [1]. В некоторых случаях у пользователей свода правил применение данной методики вызывает вопросы. С целью разъяснения и развития положений норм ниже приведены отдельные комментарии к уточненной методике свода правил по расчету наклонных сечений при действии сжимающей продольной силы.
Особенности нормативной методики расчета
Оценка наклонных сечений по прочности при действии продольных и поперечных сил, согласно СП 63.13330.2018 [1], зависит от величины сжимающей продольной силы. По результатам проведенных исследований [2][3] установлено, что с ростом сжимающей силы прочность наклонных сечений возрастает, затем при достижении определенного значения сжимающей силы наблюдается снижение несущей способности наклонного сечения. Данная зависимость отражена в своде правил в виде коэффициента φn, значение которого определяют в зависимости от величины сжимающего напряжения в бетоне σср. Таким образом, в качестве базового параметра, характеризующего величину сжимающей продольной силы, в своде правил сейчас рассматривается среднее значение сжимающего напряжения в бетоне по нормальному сечению элемента. Как уже отмечалось в [4], по сравнению с ранее действовавшей методикой, изложенной в СП 63.13330.2012 [5], в действующей редакции СП 63.13330.2018 [1] расчет по прочности наклонных сечений при действии продольных сил выполняют с учетом продольной арматуры. Это обстоятельство учтено при определении среднего значения сжимающего напряжения в нормальном сечении элемента.
Согласно методике СП 63.13330.2018 [1], среднее значение сжимающего напряжения σср допускается определять точным и приближенными методами.
Точный метод заключается в расчете нормального сечения по нелинейной деформационной модели с учетом действующих изгибающих моментов и продольной силы с определением среднего сжимающего напряжения в бетоне. При действии как сжимающей, так и растягивающей продольной силы расчет выполняют на центральное приложение продольной силы без учета влияния изгибающих моментов. Имея значение напряжения, в данном случае можно сразу определить значение коэффициента φn, исходя из следующих условий:
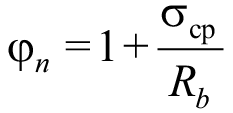 при σср ≤ 0,25Rb;
при σср ≤ 0,25Rb;
φn = 1,25 при 0,25Rb < σср ≤ 0,5Rb ; (1)
 при σср > 0,5Rb.
при σср > 0,5Rb.
При действии растягивающей продольной силы значение коэффициента φn принимают равным:
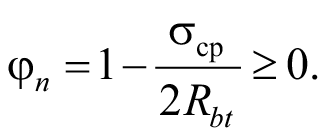 (2)
(2)
В силу того, что в практике встречаются случаи работы элементов преимущественно при действии продольных сжимающих сил, ниже основное внимание будет уделено именно этому случаю.
Очевидно, что при расчете точным методом распределение сжимающих напряжений по сечению учитывает наличие арматуры в сечении. Однако данный метод требует применения специализированных программных средств, поэтому для практического применения в своде правил был также предложен упрощенный метод.
Упрощенный метод определения средних сжимающих напряжений основан на использовании секущего модуля бетона при его деформациях, отвечающих вершине криволинейной диаграммы деформирования бетона, и позволяет учесть наличие продольной арматуры на общих принципах расчета железобетонных элементов.
В этом случае значение сжимающего напряжения определяют по формуле:
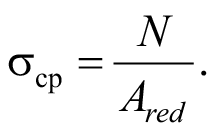 (3)
(3)
При определении сжимающего напряжения рассматривают площадь приведенного поперечного сечения элемента Ared, которую определяют с учетом арматуры, а также неупругих свойств бетона при сжатии, устанавливаемых на базе криволинейной диаграммы деформирования бетона. На основе этого в своде правил площадь приведенного поперечного сечения элемента Ared определяют по формуле:
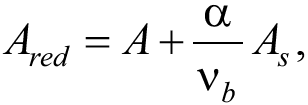 (4)
(4)
где A – площадь поперечного сечения бетона;
As – площадь всей продольной арматуры;
vb – коэффициент упругости бетона при сжатии;
α – коэффициент приведения арматуры к бетону.
Значение коэффициента упругости бетона при сжатии vb в общем случае определяют по указаниям Приложения Г к СП 63.13330.2018 [1], рассматривая полную диаграмму и вводя в нее расчетные прочностные характеристики бетона.
Однако учитывая, что при определении значения данного коэффициента используется параметр η, характеризующий уровень напряжений (т. е. искомую величину среднего напряжения), то в нормах была предложена упрощенная методика определения коэффициента упругости бетона vb. Для этого в качестве характерной точки криволинейной диаграммы рассмотрена ее вершина, положение которой характеризуется коэффициентом упругости бетона vb, определяемом при сжатии по формуле:
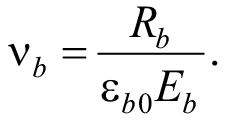 (5)
(5)
При растяжении значение коэффициента упругости бетона vbt принимают равным:
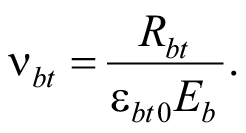 (6)
(6)
Также надо отметить, что значения относительных деформаций бетона при сжатии и растяжении εb0 и εbt0. принимают по пункту 6.1.14 свода правил для непродолжительного действия нагрузки, то есть на данный момент при длительных нагрузках учет влияния продольных сил на прочность наклонных сечений выполняется как при кратковременном действии нагрузок. Влияние длительности действия подлежит дополнительному исследованию.
Отдельно следует отметить, что по СП 63.13330.2018 [1] допускается величину σср определять без учета арматуры при содержании продольной арматуры не более 3 %, то есть принимая напряжения равными:
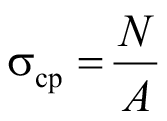 , (7)
, (7)
где A – площадь поперечного сечения элемента.
Очевидно, что все вышеуказанные методики расчета приводят к вариативности значений величины средних сжимающих и растягивающих напряжений и, соответственно, значения коэффициента φn, учитывающего ее влияние на прочность наклонного сечения.
Для удобства дальнейшего сравнения результатов методик можно их обобщить следующим образом:
– точная методика с определением средних напряжений в сечении расчетом по нелинейной деформационной модели (НДМ, далее – метод 1);
– упрощенная методика с определением среднего напряжения при помощи коэффициента секущего модуля бетона в вершине криволинейной диаграммы деформирования по формулам (4) и (5) (далее – метод 2);
– упрощенная методика с определением среднего напряжения при малом содержании арматуры по формуле (7) (далее – метод 3).
Предложенные методики позволяют выполнять расчеты по желанию пользователя норм с привлечением программных средств либо вручную. Ниже приведены результаты сравнительного анализа нормативных методик при действии сжимающего усилия. При сравнительном анализе вышеуказанных методов за эталонный был принят метод 1 – метод расчета с применением НДМ. Также при сравнении рассматривалось различное содержание арматуры – от 0,1 до 6 %.
Сравнительный анализ метода 1 (НДМ) и метода 2 (с определением коэффициента секущего модуля бетона по вершине криволинейной диаграммы) показал, что отклонения значений средних сжимающих напряжений носят криволинейный характер: при малых уровнях напряжений напряжения по упрощенному методу 2 ниже, чем по НДМ (от 2 % до 1,8 раза в зависимости от содержания арматуры), с ростом уровня обжатия разница нивелируется. Сравнение средних сжимающих напряжений по НДМ и упрощенному методу 3 показывает обратное: с ростом уровня обжатия сечения разница существенно увеличивается, при высоком уровне она может достигать до 2-х раз и более. На рис. 1–3 приведены зависимости для соотношений средних напряжений по упрощенным модикам к напряжениям, полученным по НДМ при различном содержании арматуры.
При сравнении значений напряжений по различным методикам при N = Nult видно, что значение соотношения напряжений по упрощенному методу 2 (по вершине диаграммы) и по НДМ равно единице. Учитывая, что сравнительный анализ значений напряжений в данном случае был выполнен на конкретных примерах с округлением напряжений до десятых долей, а также, что сравнение нулевых значений напряжений между собой математически невозможно, это нашло отражение на графиках на рис. 1–3. Также при сравнительном анализе методик на рис. 1–3 и ниже учитывалась область применения упрощенной методики 3, то есть при содержании арматуры более 3 % данная методика в анализе не рассматривалась.
Весьма наглядной является вторая упрощенная методика (метод 3), при которой не учитывается влияние продольной арматуры. При малом содержании арматуры (1 % и менее) методика оценивает значения средних напряжений выше (до 20 %), чем по НДМ. С увеличением содержания арматуры до 3–5 % значения средних напряжений по данной методике могут превышать напряжения в бетоне, полученные с применением НДМ, до 2-х раз и выше. Очевидно, что при всей простоте расчета это делает методику весьма осторожной и позволяет использовать ее для быстрой предварительной оценки прочности наклонных сечений с учетом влияния продольных сил.
Указанная особенность по отклонению значений напряжений при упрощенной методике от значений напряжений, полученных при расчете по НДМ, имеет отражение и при определении значения коэффициента φn. Как видно из зависимости (1), в своде правил принята трехлинейная диаграмма зависимости несущей способности наклонного сечения, характеризуемого коэффициентом φn, от уровня обжатия продольной силой, выраженной через соотношение средних напряжений к прочности бетона (рис. 4). При действии продольных растягивающих сил диаграмма имеет вид линейно падающей функции (рис. 5).
Видно, что диаграмма для коэффициента φn при действии сжимающих продольных сил имеет высокую чувствительность на ниспадающей ветви при высоком уровне сжимающих напряжений σср > 0,5Rb. Незначительное отклонение величины среднего напряжения именно в этой области может привести к существенному отклонению в значении коэффициента φn. В связи с этим при проектировании конструкций по наклонному сечению с высоким уровнем сжимающих напряжений, отвечающим предельной стадии работы нормального сечения элемента, может возникнуть ситуация, когда значения коэффициента φn при определении напряжений в бетоне по НДМ в предельной стадии могут быть существенно ниже, чем при определении напряжений по упрощенной методике 2, когда для оценки напряжений используется вершина криволинейной диаграммы. Надо отметить, что данная ситуация имеет место только для конструкций при содержании арматуры более 1 % и при уровне сжимающих напряжений от 70 % и выше. Графическое сравнение значений коэффициентов φn при действии сжимающих продольных сил, определенных по трем указанным методикам при различном содержании арматуры, приведено на рис. 6–9.
Из приведенных на рис. 6–9 значений коэффициентов φn видно, что при малом содержании арматуры в элементах упрощенные методики показывают хорошую сходимость с методикой, основанной на определении средних напряжений по НДМ. С ростом содержания арматуры при малых уровнях нагружения (до уровня σср < 0,5Rb) расхождение в методиках также несущественно и составляет в среднем около 3 %.
Однако также видно, что с увеличением содержания арматуры (выше 1 %) при высоком уровне сжимающих напряжений значения коэффициентов φn, полученные с применением упрощенной методики 2, могут превышать до двух раз соответствующие значения коэффициентов, полученных с применением НДМ. Можно обратить внимание, что эта погрешность существенна при весьма малых абсолютных значениях данного коэффициента, отвечающих высокому уровню обжатия, то есть на стадии, близкой к разрушению элемента по нормальному сечению. Данное обстоятельство требует дополнительной проверки, особенно учитывая хрупкий характер работы, для конструкций из высокопрочных бетонов при действии поперечных сил.
Второй упрощенный метод (метод 3), когда напряжения определяют по формуле (7) без учета продольной арматуры, всегда дает осторожные решения по значениям коэффициента φn по сравнению со всеми остальными методиками.
Дополнительно можно отметить, что при определении площади поперечного сечения A отдельные пользователи свода правил также учитывают площадь продольной арматуры As, которая замещает часть бетона в сечении, вычитая ее из общей площади поперечного сечения. Анализ показывает, что при использовании упрощенной методики данным обстоятельством можно пренебречь, так как даже при существенном содержании арматуры (порядка 6 %) отклонения в результатах при определении среднего сжимающего напряжения σср будут составлять не более 3 %.
Отдельно следует обратить внимание на то, что величина среднего напряжения определяется из оценки напряженно-деформированного состояния нормального сечения. Соответственно, в условиях методики расчета прочности наклонных сечений, когда рассматривают ряд наклонных сечений по длине пролета среза, это приводит к необходимости назначения положения нормального сечения в рамках пролета среза, в котором будет определяться значение среднего напряжения в бетоне, что также может влиять на корректность оценки прочности наклонных сечений с учетом действия продольных сил.
Нельзя не заметить, что в нормах сейчас имеется ситуация, при которой упрощенная методика определения величины сжимающих напряжений с применением коэффициента упругости бетона, определяемого по вершине криволинейной диаграммы (методика 2), показывает приемлемую сходимость для элементов с малым содержанием арматуры (до 1 %) по сравнению с точным определением напряжений по НДМ. Однако с ростом содержания арматуры до 6 % расхождение значений коэффициентов φn по точной методике и упрощенной методике 2 увеличивается. Причем одновременно с увеличением армирования наблюдается снижение уровня нагружения, при котором увеличивается это расхождение – от 0,94 при μ = 1 % до 0,8 при μ = 6 % соответственно. Графически отклонения значений по упрощенной методике 2 от НДМ при различном содержании армирования приведены на рис. 10.
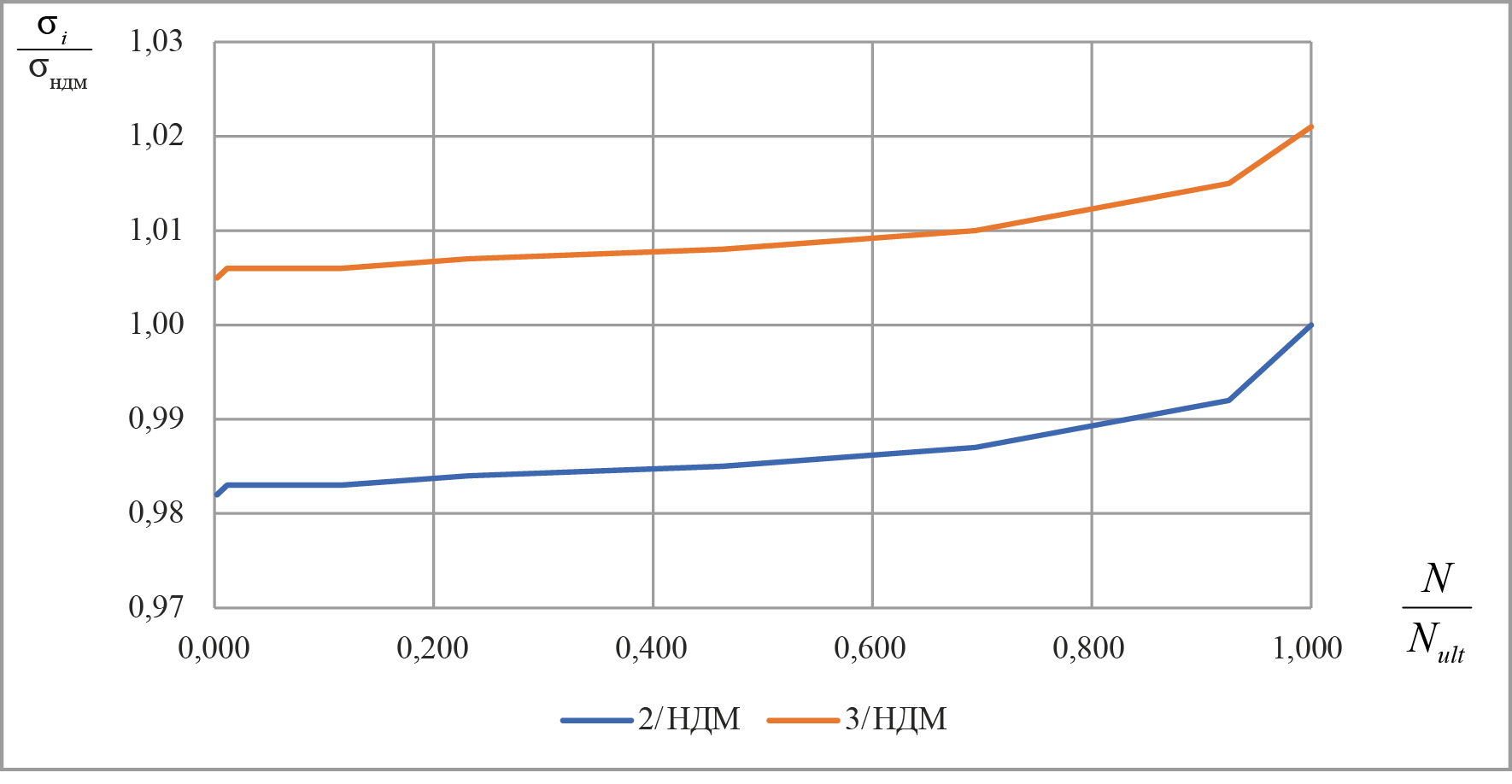
Рис. 1. Соотношение значений средних сжимающих напряжений, определяемых по различным методикам, при содержании арматуры 0,1 %: σi – напряжения, определяемые по упрощенным методам (методы 2 и 3); σндм – напряжения, определяемые по НДМ
Fig. 1. Ratio of average compressive stresses determined by various methat a reinforcement content of 0.1 %: σi – stresses determined by simplified methods 2 and 3; σNSSM – stresses determined by the Nonlinear Stress-Strain Model

Рис. 2. Соотношение значений средних сжимающих напряжений, определяемых по различным методикам, при содержании арматуры 3 %: σi – напряжения, определяемые по упрощенным методам (методы 2 и 3); σндм – напряжения, определяемые по НДМ
Fig. 2. Ratio of average compressive stresses determined by various methods at a reinforcement content of 3 %: σi – stresses determined by simplified methods 2 and 3; σNSSM – stresses determined by the Nonlinear Stress-Strain Model
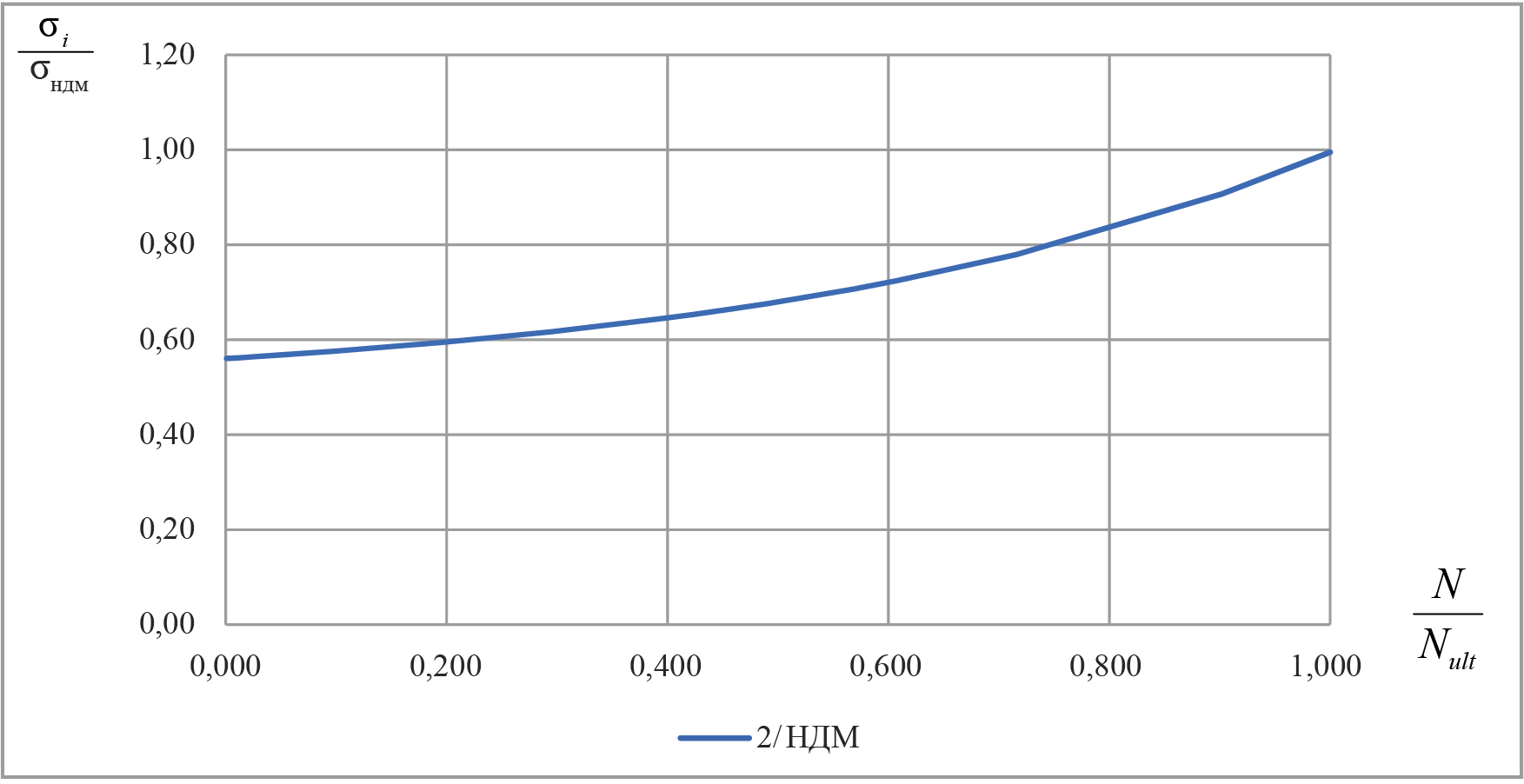
Рис. 3. Соотношение значений средних сжимающих напряжений, определяемых по методу 2, при содержании арматуры 6 %: σi – напряжения, определяемые по упрощенному методу 2; σндм – напряжения, определяемые по НДМ
Fig. 3. Ratio of average compressive stresses determined by the method 2 at a reinforcement content of 6 %: σi – stresses determined by the simplified method 2; σNSSM – stresses determined by the Nonlinear Stress-Strain Model
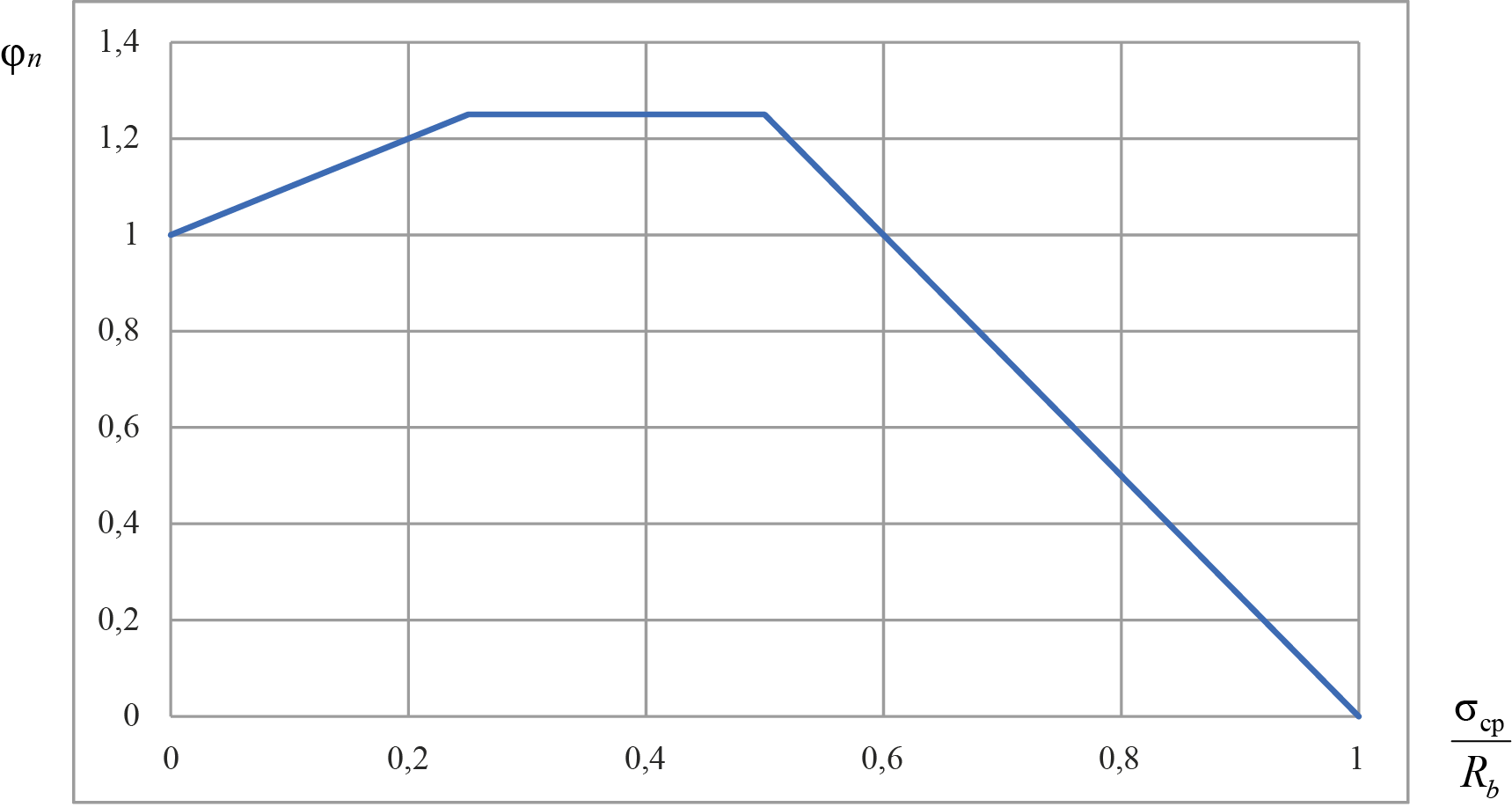
Рис. 4. Нормативная зависимость значения коэффициента φn при действии продольных сжимающих сил от соотношения σср/Rb
Fig. 4. Standard dependence of the coefficient φn on the ratio σav/Rb under the action of longitudinal compressive forces
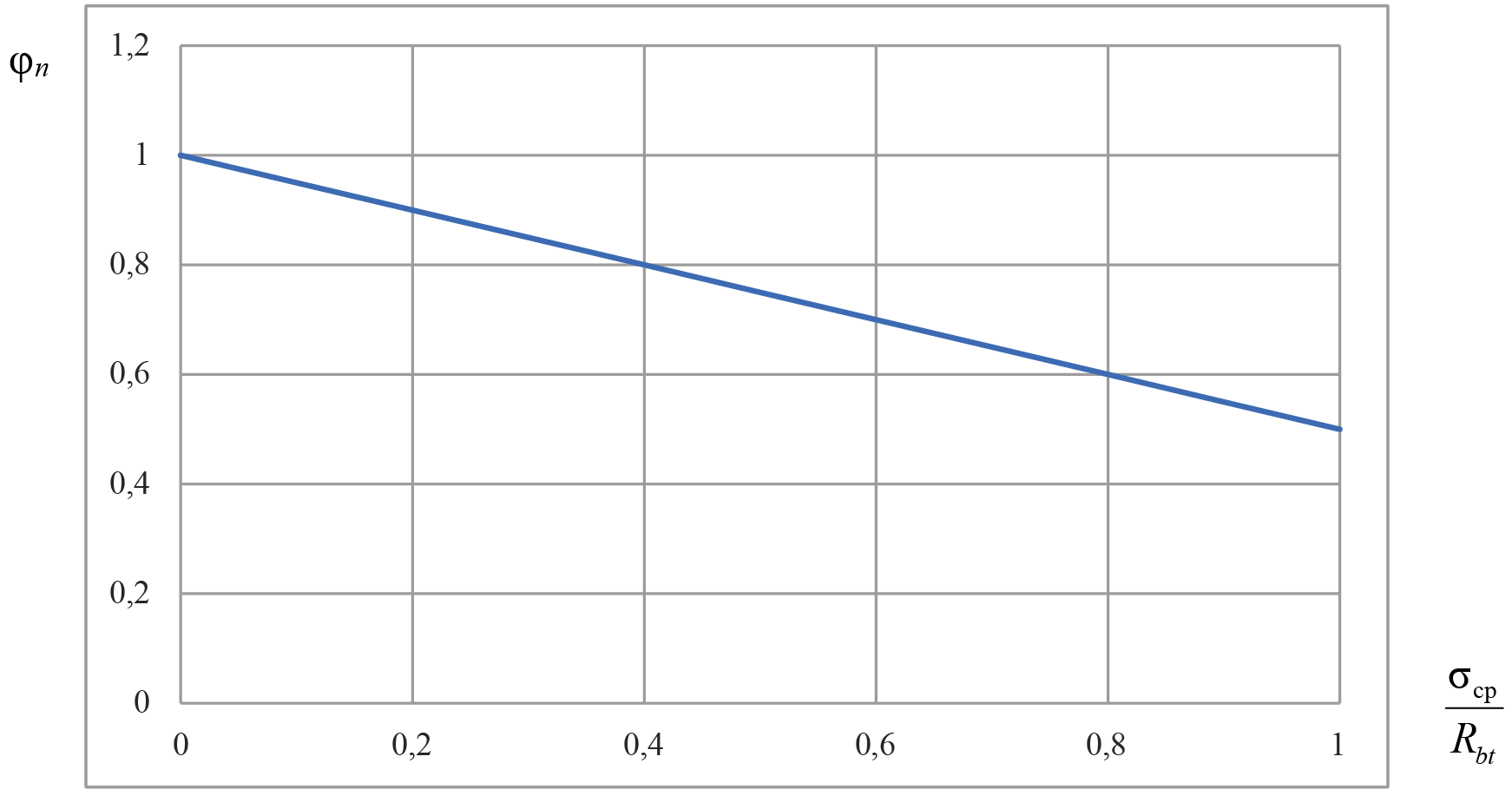
Рис. 5. Нормативная зависимость значения коэффициента φn при действии продольных растягивающих сил от соотношения σср/Rbt
Fig. 5. Standard dependence of the coefficient φn on the ratio σav/Rbt under the action of longitudinal tensile forces
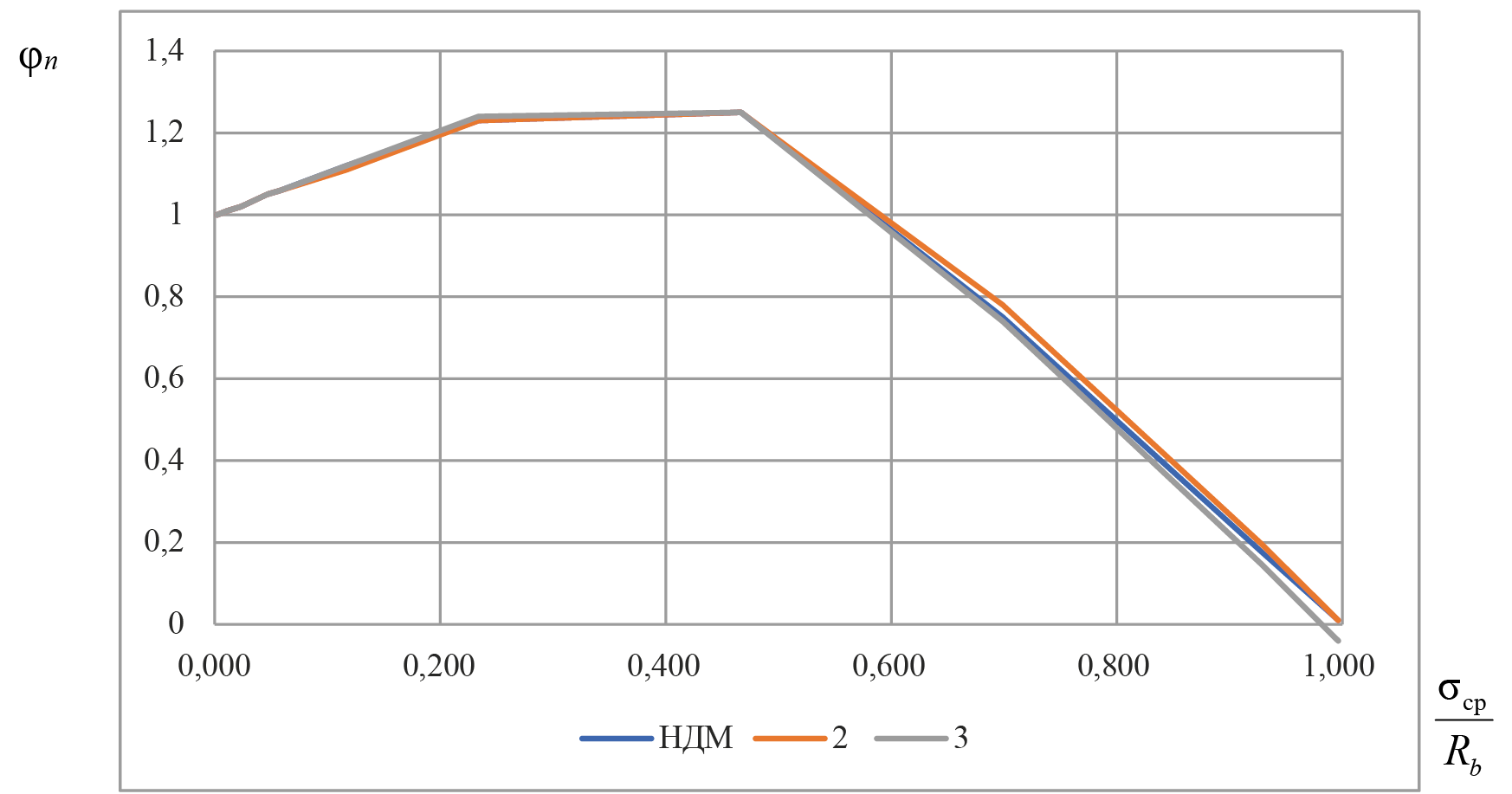
Рис. 6. Значения коэффициентов φn при действии сжимающих продольных сил, определенных по НДМ и упрощенным методикам с учетом продольной арматуры (2) и без нее (3), при содержании арматуры 0,1 %
Fig. 6. Coefficients φn under the action of compressive longitudinal forces: alculation according to the Nonlinear Stress-Strain Model and simplified methods with (2) and without (3) longitudinal reinforcement at a reinforcement content of 0.1 %
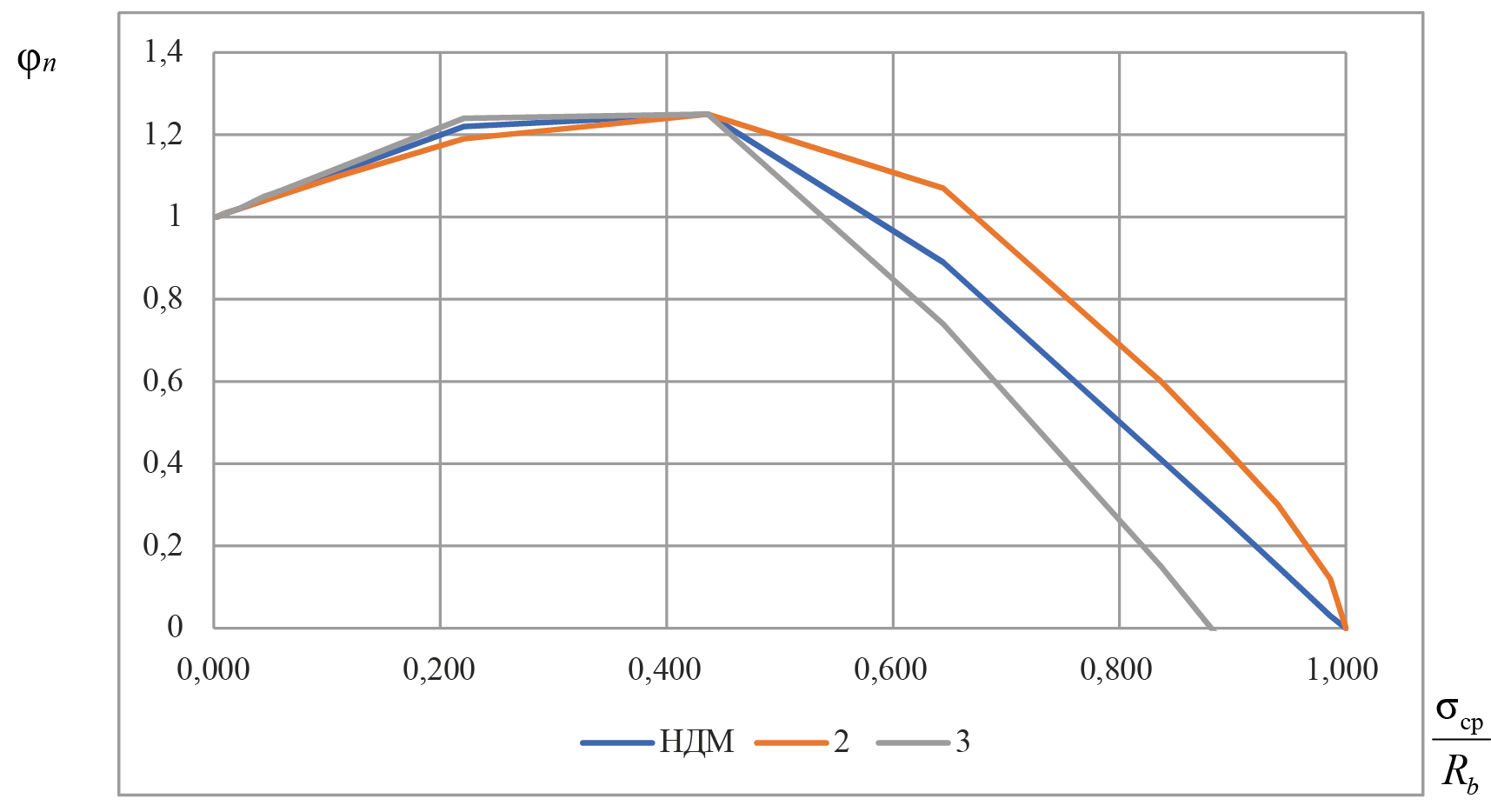
Рис. 7. Значения коэффициентов φn при действии сжимающих продольных сил, определенных по НДМ и упрощенным методикам с учетом продольной арматуры (2) и без нее (3), при содержании арматуры 1 %
Fig. 7. Coefficients φn under the action of compressive longitudinal forces: calculation according to the Nonlinear Stress-Strain Model and simplified methods with (2) and without (3) longitudinal reinforcement at a reinforcement content of 1 %
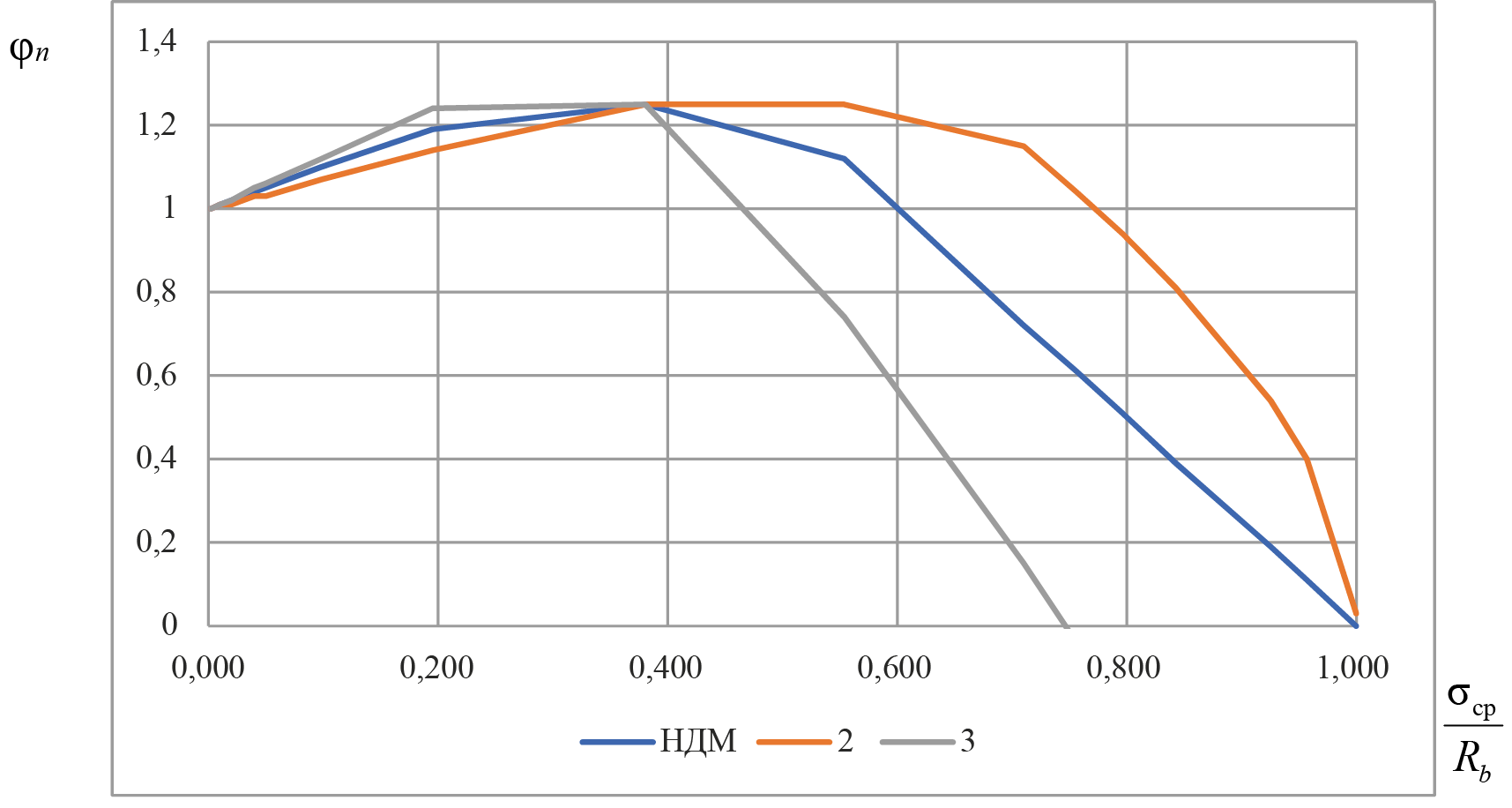
Рис. 8. Значения коэффициентов φn при действии сжимающих продольных сил, определенных по НДМ и упрощенным методикам с учетом продольной арматуры (2) и без нее (3), при содержании арматуры 3 %
Fig. 8. Coefficients φn under the action of compressive longitudinal forces: calculation according to the Nonlinear Stress-Strain Model and simplified methods with (2) and without (3) longitudinal reinforcement at a reinforcement content of 3 %

Рис. 9. Значения коэффициентов φn при действии сжимающих продольных сил, определенных по НДМ и упрощенной методике с учетом продольной арматуры (2), при содержании арматуры 6 %
Fig. 9. Coefficients φn under the action of compressive longitudinal forces: calculation according to the Nonlinear Stress-Strain Model and simplified method taking into account longitudinal reinforcement (2) at a reinforcement content of 6 %
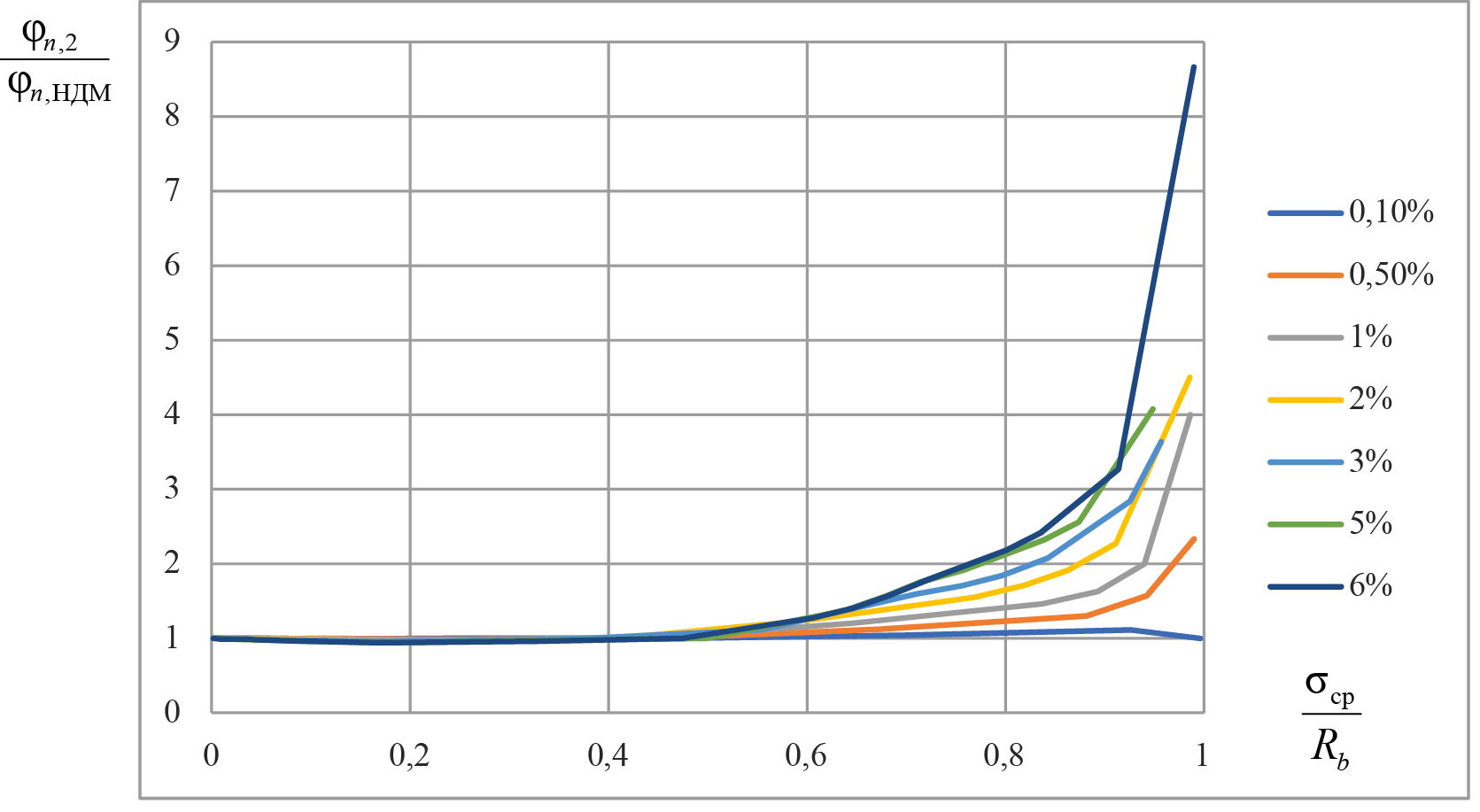
Рис. 10. Отклонения значений коэффициентов φn при действии сжимающих продольных сил, определенных по НДМ и упрощенной методике с учетом продольной арматуры (2), при различном содержании арматуры
Fig. 10. Deviation of coefficients φn under the action of compressive longitudinal forces: calculation according to the Nonlinear Stress-Strain Model and simplified method taking into account longitudinal reinforcement (2) at various reinforcement contents
Выводы
Анализ нормативных методов расчета прочности наклонных сечений с учетом влияния продольных сил показывает, что при использовании отдельных упрощенных методов определения значений средних сжимающих напряжений при высоком уровне обжатия в ряде случаев могут наблюдаться существенные расхождения в оценке прочности наклонных сечений. Учитывая возможность хрупкого разрушения при действии поперечных сил, это показывает необходимость проведения дальнейших исследований данного вопроса, включая конструкции из высокопрочных бетонов. Соответственно, с целью обеспечения необходимого уровня надежности и конструктивной безопасности железобетонных элементов действующая методика расчета наклонных сечений с учетом продольных сил также требует дальнейшей проработки и совершенствования, в том числе с верификацией опытными исследованиями.
Список литературы
1. СП 63.13330.2018. Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52-01-2003. Москва: Стандартинформ; 2019.
2. <i>Зенин С.А., Шарипов Р.Ш., Кудинов О.В.</i> Влияние сжимающих напряжений на прочность наклонных сечений внецентренно сжатых железобетонных элементов. Бетон и железобетон. 2021;603(1):44–51.
3. <i>Мухамедиев Т.А., Зенин С.А.</i> Учет влияния продольных сил при расчете железобетонных конструкций по наклонным сечениям. В: Современные проблемы расчета и проектирования железобетонных конструкций многоэтажных зданий: сб. док. Междунар. науч. конф., посвященной 100-летию со дня рождения П.Ф. Дроздова. Москва: Московский государственный строительный университет; 2013, с. 170–174.
4. <i>Зенин С.А.</i> К вопросу расчета железобетонных конструкций на действие изгибающих моментов, продольных и поперечных сил по СП 63.13330.2018. Бетон и железобетон. 2023;616(2):50–55. https://doi.org/10.37538/0005-9889-2023-2(616)-50-55.
5. СП 63.13330.2012. Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52-01-2003. Москва: Минстрой России; 2015.
Об авторах
С. А. ЗенинРоссия
Сергей Алексеевич Зенин*, канд. техн. наук, заведующий лабораторией теории железобетона и конструктивных систем, НИИЖБ им. А.А. Гвоздева АО «НИЦ «Строительство», Москва
2-я Институтская ул., д. 6, к. 5, г. Москва, 109428, Российская Федерация
e-mail: lab01@mail.ru
Т. А. Мухамедиев
Россия
Тахир Абдурахманович Мухамедиев, д-р техн. наук, главный научный сотрудник лаборатории теории железобетона и конструктивных систем, НИИЖБ им. А.А. Гвоздева АО «НИЦ «Строительство», Москва
2-я Институтская ул., д. 6, к. 5, г. Москва, 109428, Российская Федерация
e-mail: takhir50@rambler.ru
А. А. Семенов
Россия
Алексей Александрович Семенов, инженер 2-й категории центра проектирования и экспертизы, НИИЖБ им. А.А. Гвоздева АО «НИЦ «Строительство»; аспирант, АО «НИЦ «Строительство», Москва
2-я Институтская ул., д. 6, к. 5, г. Москва, 109428, Российская Федерация; 2-я Институтская ул., д. 6, к. 1, г. Москва, 109428, Российская Федерация
e-mail: alexi-1999@mail.ru
Рецензия
Для цитирования:
Зенин С.А., Мухамедиев Т.А., Семенов А.А. Особенности методики расчета по прочности наклонных сечений железобетонных конструкций на действие поперечных и продольных сил по СП 63.13330.2018. Вестник НИЦ «Строительство». 2025;47(4):19-32. https://doi.org/10.37538/2224-9494-2025-4(47)-19-32. EDN: GODWIA
For citation:
Zenin S.A., Mukhamediev T.A., Semenov A.A. Features of calculating the strength of inclined sections for reinforced concrete structures under transverse and longitudinal forces according to SP 63.13330.2018. Bulletin of Science and Research Center of Construction. 2025;47(4):19-32. (In Russ.) https://doi.org/10.37538/2224-9494-2025-4(47)-19-32. EDN: GODWIA
JATS XML


























