Перейти к:
Эффекты при отражении волны напряжений в деревянных образцах
https://doi.org/10.37538/2224-9494-2025-4(47)-132-143
EDN: SMJSPD
Аннотация
Введение. Волновые процессы распространения напряжений и деформаций в древесине как в конструкционном материале имеют свои особенности. Геометрическая форма элементов деревянных конструкций как граница физических сред, конструктивная форма узлов и соединений, обычно из стальных элементов, клеевые слои, слои модифицированной клеем древесины создают сложные граничные условия развития напряженно-деформированного состояния.
Цель. Обоснование модели процесса отражения волны напряжения от границы среды в деревянном образце, с качественной и количественной оценками изменения напряжения во времени и по геометрической длине образца. Модель деформирования древесины как природного полимера позволит на основе кинетической теории прочности обосновать длительную прочность древесины и деревянных конструкций.
Материалы и методы. Проанализированы исследования Г. Кольского, Р.М. Дейвиса, Ю.Н. Работнова в части обоснования предложенной модели волновых процессов в древесине и деревянных конструкциях. Дополнительно обоснована гипотеза о влиянии волнового распространения деформаций на длительную прочность. Численный эксперимент показал эффекты при отражении волны напряжений от границ принятой упругой ограниченной среды. Предложены две новые гипотезы: в зависимости от физических свойств материала и геометрических размеров элемента строительной конструкции, а также величины и продолжительности приложения внешней нагрузки может быть определен так называемый «порог глубины», глубже которого начинает проявляться полный волновой эффект распространения напряжения в объеме образца; тороидальное тело с длиной, многократно превышающей его диаметр, стремящейся к бесконечности, можно считать цилиндром бесконечной длины, моделирующей бесконечную среду.
Результаты. Напряжения распространяются в объеме образца волнообразно, постепенно затухая до значения в 27 МПа эквивалентного напряжения по Мизесу, в состоянии покоя нагруженного образца. Напряжения на поверхности приложения внешней нагрузки стабилизируются быстрее, волновые процессы изменения напряжений характеризуются незначительной амплитудой.
Выводы. В численном и натурном экспериментах выявлена закономерность, подтвердившая ранее сформулированную гипотезу о значительном превышении значения волны напряжения над величиной напряжения в состоянии покоя нагруженного элемента. При сжатии образца выявлен эффект колебания волны напряжения отражения, амплитуда которой устанавливается относительно значения напряжения в состоянии покоя.
Ключевые слова
Для цитирования:
Романов П.Г., Слепцов А.А. Эффекты при отражении волны напряжений в деревянных образцах. Вестник НИЦ «Строительство». 2025;47(4):132-143. https://doi.org/10.37538/2224-9494-2025-4(47)-132-143. EDN: SMJSPD
For citation:
Romanov P.G., Sleptsov A.A. Effects of stress wave reflection in wooden samples. Bulletin of Science and Research Center of Construction. 2025;47(4):132-143. (In Russ.) https://doi.org/10.37538/2224-9494-2025-4(47)-132-143. EDN: SMJSPD
Введение
Волновые процессы распространения напряжений и деформаций в древесине как в конструкционном материале имеют свои особенности. Продольные волны, у которых направления колебаний совпадают с направлением движения; поперечные волны, колебания которых перпендикулярны направлению их распространения. Возникая, распространяясь, ограничиваясь и затухая в объеме элемента деревянной конструкции, они претерпевают изменения своих характеристик, обусловленные физическими свойствами древесины и формой элементов строительной конструкции. В большинстве случаев геометрическая форма элементов деревянных конструкций как граница физических сред, конструктивная форма узлов и соединений, обычно из стальных узлов, клеевые слои, слои модифицированной клеем древесины создают сложные граничные условия развития напряженно-деформированного состояния.
Основные волновые реактивные явления отражения от границы сред, взаимодействия сред при внешних воздействиях описаны преимущественно в стали и железобетоне.
Целью работы является обоснование модели процесса отражения волны напряжения от границы среды в деревянном образце, с качественной и количественной оценками изменения напряжения во времени и по геометрической длине образца. Модель деформирования древесины как природного полимера позволит на основе кинетической теории прочности обосновать длительную прочность древесины и деревянных конструкций.
Материалы и методы
Классификация волновых процессов в курсах классической физики разделяет упругие физические среды на неограниченные среды и на среды, имеющие свободную поверхность или имеющие поверхность раздела двух тел, как правило, имеющих различные физические свойства [1].
Волновой процесс характеризуется преодолением сопротивления среды, наличием внутреннего или внешнего трений, передачей части внутренней энергии внешней среде в виде тепла, изменением внутреннего температурного и энергетического балансов. Уменьшаются скорость и амплитуда волны, происходит затухание волны.
Важной характеристикой процесса потери энергии волн является коэффициент затухания, имеющий разные размерности в зависимости от условий и среды распространения. Определенный показатель волны (например, амплитуда колебания или др.), отнесенный к единице длины или времени, характеризует затухание как физический процесс. В механике коэффициент затухания имеет размерность, обратную времени, – сек-1. Если затухание оценивается как убывание рассматриваемой характеристики, например амплитуды на единицу длины, то величина будет безразмерной.
Поскольку рассматривается задача распространения волны напряжений и деформаций в сплошной упруго-пластической среде, оценим затухание волн в выбранной реологической модели среды сопротивления. Для оценки сопротивления материалов во времени приняты различные реологические модели:
– тело Гука, H (упругое тело);
– тело Ньютона, N (упруго-пластическое тело);
– тело Сен-Венана, StV (упругое тело, применимо к упруго-пластическим телам);
– тело Журкова, Zh (пластическое тело, применимо к упруго-пластическим телам);
– тело Кауцманна, Km (пластическое тело);
– тело Максвелла (Фойгта), MF (вязко-упругое тело);
– составное тело, PM (physical medium), с задаваемыми характеристиками.
В некоторых задачах модели вязко-упругих тел детализированы как тело Кельвина – Фойгта, тело Максвелла и стандартное линейное тело [2]. Рассматривается и более общая модель, объединяющая свойства указанных моделей [1].
При этом модель физического тела, выбираемая для конкретной задачи, должна с допустимой корректностью отражать изменение характеристик упруго-пластических свойств материала в процессе сопротивления элементов реальных строительных конструкций.
В реальных условиях сопротивления элементов строительных конструкций из различных материалов, в частности деревянных конструкций, их объемы ограничены, объемные формы элементов конструкций известны. Формулировка заданий на численное моделирование процессов изменения напряженно-деформированного состояния, составление граничных условий основываются на особенностях нагружения, сопротивления материала и конструктивной формы элемента строительной конструкции.
Численный эксперимент
Авторами принята модель тела по аналогии с телом Гука, H (упругое тело, работает в упругой стадии, упруго-пластические и пластические свойства в данной задаче не рассматриваются). Поскольку скорость распространения волны напряжения в древесине велика, сопоставима со скоростью распространения звука в древесине (по справочным данным в интервале от 1000 до 5000 м/сек), сопротивление происходит упруго. Пластические деформации не проявляются, происходит своеобразное запаздывание пластичности аналогично данному эффекту в малоуглеродистных сталях. Данный эффект пресдтавлен Ю. Н. Работновым: «… Характерная особенность малоуглеродистых сталей – это так называемое запаздывание текучести. Как оказывается при кратковременном действии нагрузки, вызывающей напряжения, значительно превышающее статический предел текучести, материал может оставаться некоторое непродолжительное время в упругом состоянии. Под статическим пределом текучести мы понимаем условную величину, измеряемую в обычных опытах на стандартном оборудовании. Непродолжительное время нужно понимать в том смысле, что эффект запаздывания заметен при временах порядка микро- миллисекунд, т. е. главным образом в волновых процессах…» [3].
В предыдущих задачах [4–10] реализованы этапы последовательного приближения численных моделей к работе реальных деревянных цельных и клееных элементов, при восприятии ими волнового воздействия напряжений в объеме элементов деревянных конструкций. Численные эксперименты показали качественную и количественную картины распространения деформаций и их волновых проявлений. Выявлено значительное влияние пропорций образца (отношения его ширины и длины (возможно толщины)) на интерференцию волн на поверхности. Качественная картина показывает, что при количественном описании градиента деформации могут быть выделены опасные для материала участки. Расчетным путем будет возможно определить участки с наибольшими градиентами деформаций и принять конструктивные меры недопущения отказов деревянных однонаправленно и перекрестно склеенных панельных конструкций. Рассмотренная модель деревянного анизотропного стержня близка к первой гипотезе безграничной упругой среды, так как исключено рассмотрение колебаний точки в других направлениях.
Далее линейные задачи расширены до демонстрации пространственных деформаций. Модели демонстрируют распространение продольной и поперечной волн, представляют объемную деформацию анизотропного материала. В плоскости, совпадающей с направлением распространения волны, представлено уплотнение и разрежение среды. В этой же системе координат представлены графики изменения амплитуды поперечной волны. Совмещение этих двух графиков показывает разность скоростей распространения волн и сочетание амплитуд. Модель позволяет выделить наличие отраженных волн Релея, описать отражение волн от границы среды. Визуализация волнообразного распространения напряжений и деформаций требует дальнейшей детализации, формулировки граничных условий и ограничений.
Численный эксперимент реализован на языке с++ с помощью специализированного пакета для вычисления дифференциальных уравнений FEniCS. Поскольку нагрузка прикладывается вдоль оси Z, основной интерес представляет скорость волны, распространяющейся в этом направлении.
Численный эксперимент моделирует процесс сопротивления цельнодеревянного образца с размерами a × b × h, 100 × 100 × 150 мм, нагружаемого осевой силой в 40 тонн. Нагрузка прикладывается внезапно (импульсно, за короткое время), за 10 микросекунд. Продолжительность описания процесса волнового распространения напряжений до наступления стабильного состояния покоя колеблется около 60 сек, в зависимости от заданных условий. Характерные точки обозначены на вертикальной осевой линии срединной плоскости образца (рис. 1). Это три точки – на свободной площадке приложения нагрузки, в середине и у опоры. Искомое значение напряжения в точке, если воспользоваться условием прочности по Мизесу, как эквивалентное напряжение с учетом составляющих нормальных напряжений по осям X, Y и Z определяется по формуле:
(σ1 – σ2) 2 + (σ2 – σ3) 2 + (σ3 – σ2) 2 = 2σт 2. (1)
Получены графики нормальных напряжений в указанных точках (рис. 2). Значения напряжений в точках вычислены по формуле (1). Скорость волны напряжения c0 принимается из известной зависимости, по модулю упругости и плотности древесины сосны:
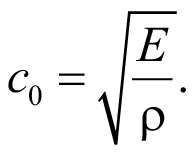 (2)
(2)
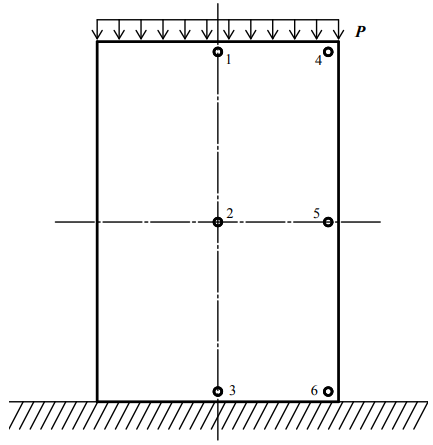
Рис. 1. Схема нагружения и характерные точки
Fig. 1. Loading diagram and characteristic points
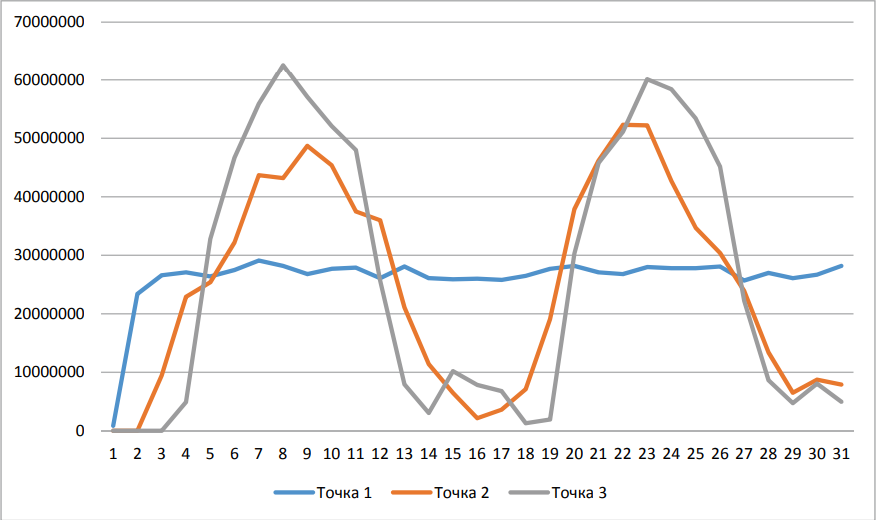
Рис. 2. Движение волны напряжений во времени, в сечениях образца, Па
Fig. 2. Movement of stress waves over time, in sample sections, Pa
На основании графиков волноообразного изменения напряжений возможно сформулировать следующие результаты:
– напряжения распространяются в объеме образца волнообразно, постепенно затухая до расчетного значения напряжения нагруженного образца в состоянии покоя в 27 МПа;
– напряжения на поверхности приложения внешней нагрузки стабилизируются быстрее, волновые процессы изменения напряжений характеризуются незначительной амплитудой;
– напряжения в срединной и в приопорной частях объема образца демонстрируют колебания в значительных пределах.
На основании полученных результатов возможна формулировка сопровождающей гипотезы: в зависимости от физических свойств материала и геометрических размеров элемента строительной конструкции, а также величины и продолжительности приложения внешней нагрузки может быть определен так называемый «порог глубины», глубже которого начинает проявляться полный волновой эффект распространения напряжения в объеме образца.
Эксперименты по изучению особенностей разрушения, вызванного волновым распространением напряжений на стальных образцах, показали, что общая картина разрушения при статическом нагружении отличается от разрушения, вызванного волновым воздействием напряжений. Г. Кольский отмечает: «Так, при очень высоких скоростях нагружения, связанных с интенсивными импульсами напряжения, материалы, которые обычно считаются вязкими, могут вести себя как хрупкие»… «Это объясняется тем, что напряжение прикладывается на такой короткий промежуток времени, что ни одна из образующихся трещин не успевает распространиться, и вместо непрерывных трещин возникает большое число отдельных трещин, причем иногда они соединяются и образуют более или менее непрерывную поверхность с беспорядочной текстурой» [1].
Вибрационные испытания
В первую очередь нужно было определить коэффициент затухания деформаций, проверить экспериментально и использовать в численных исследованиях для обеспечения корректной физической картины деформирования анизотропной панели. Научная новизна исследования заключается в постановке новой научной проблемы изучения волновых процессов в перекрестноклееной древесине в конструкциях с их применением, влияния волновых процессов на длительную прочность древесины и деревянных конструкций. Выявлены и описаны новые закономерности в распространении волн напряжений и деформаций и перекрестноклееной древесине, отличающиеся от аналогичных процессов в других строительных материалах наличием анизотропии строения.
В целях определения показателей затухания были проведены вибрационные испытания на цельнодеревянных образцах с использованием измерительного комплекса ВС-301 производства ООО «ВИСОМ» (Смоленск) (рис. 3). Результаты, полученные на образцах с размерами 1200 × 70 × 50 и 2200 × 150 × 75 мм, представляют собой акселерограммы (рис. 4, 5). Образцы подвешиваются на пружинных или резиновых подвесах с целью исключения влияния реакций опор, внешних вибраций. Так называемое «обезвешивание» образцов позволяет исключить внешние воздействия. Не критично, но желательно распределить подвесы таким образом, чтобы обеспечить равномерное опирание с целью распределения изгибающих моментов от действия собственного веса образца. Вибрационные датчики регистрируют ускорения, полученные массивы данных обрабатываются для достижения целей эксперимента.
Были произведены серии ударов с разных направлений и разной силы. Установлено три датчика по длине бруса. Произведено вывешивание для отвязки частот подвеса от собственных частот колебания бруса. Таким образом, не происходит влияния опоры на распространение волн (рис. 6).
Проведен анализ результатов, позволяющий при помощи корреляционных функций между датчиками рассчитать скорость распространения волны. С помощью автокорреляционных и автоковариационных функций рассчитано эхо – отражение волны от противоположного удару конца. Для расчета добротности и логарифмического коэффициента затухания требуется возбуждение сигналом сложной формы, желательно шумоподобным. Это позволяет четко выделять корреляционные пики в отличие от ударов и синуса, которые дают размытый гармонический сигнал на корреляционной функции.
На временном сигнале на рис. 7 видно эхо от распространения волны. По этому графику оценку можно провести приблизительно, так как при ударе нет четких границ начала и окончания, они не выделяются на фоне прочих колебаний. Расчетная скорость распространения равна (4 м/0,0035) c0 = 1145 м/с, коэффициент затухания с учетом отражения равен γ = 2,5. В результате была выбрана оптимальная сила воздействия, при которой наблюдается эхо. Отражения ведут себя нелинейно и при ударах слабой интенсивности не наблюдаются. Зависимость отражений от интенсивности воздействия требует дополнительного изучения.

Рис. 3. Подготовка к вибрационным испытаниям
Fig. 3. Preparation for vibration tests
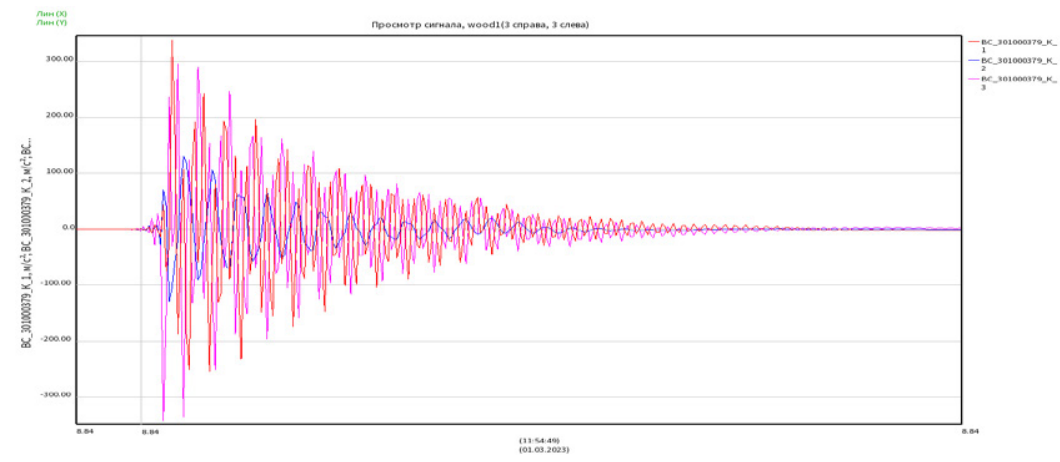
Рис. 4. Акселерограммы от единичного импульса. Последовательное расположение трех датчиков
Fig. 4. Single pulse accelerograms. Serial arrangement of three sensors

Рис. 5. Вибрационные колебания. Амплитуды ускорений (а), скоростей (б) и перемещений (в)
Fig. 5. Vibrational oscillations. Amplitudes of accelerations (a), velocities (b), and movememnts (c)

Рис. 6. Вывешивание деревянного образца размером 2200 × 150 × 75 мм
Fig. 6. Hanging a wooden sample measuring 2200 × 150 × 75 mm
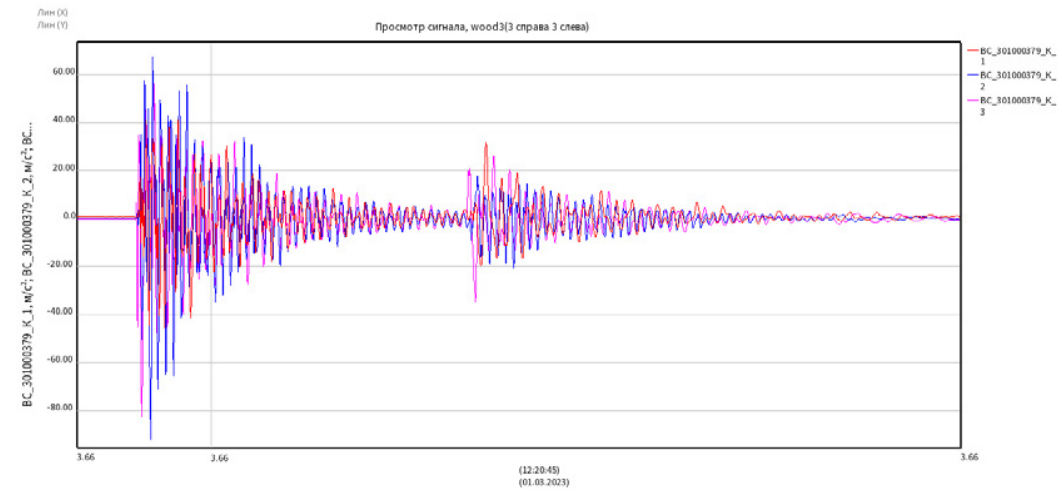
Рис. 7. Характерная картина визуализации эха
Fig. 7. Characteristic echo visualization pattern
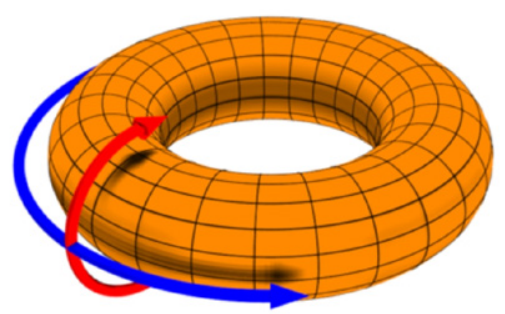
Рис. 8. Тороидальное тело (автор DaveBurke, Wikipedia)
Fig. 8. Toroidal body (by DaveBurke, Wikipedia)
Модель безграничной среды
В этой связи возникает вопрос учета наличия эха, устранения шумов и помех, в основном обусловленных ограниченностью длины испытуемого образца. Данный вопрос может быть решен применением замкнутого по длине кольцеобразного образца круглого сечения тороидальной формы (рис. 8). Длина тороидального тела должна значительно превышать его диаметр. Как подтверждает Г. Кольский, ряд ранее высказанных гипотез: «… теоретически допустимо рассматривать (прямолинейный, прим. П. Г. Романова) цилиндр таким же методом как безграничную среду. …Тогда, если мы рассмотрим возмущение в некоторой точке внутри цилиндра, то обнаружим, что из этой точки должна распространяться сферическая волна расширения со скоростью с1; часть этой волны должна распространяться вдоль цилиндра, не испытывая отражений от поверхности» [1]. Отсутствие отражения от границы сред и волн Релея (отраженных волн) является одной из главных характеристик безграничной среды. Тороидальное тело с длиной, стремящейся к бесконечности, многократно превышающей его диаметр, можно считать цилиндром бесконечной длины.
Поскольку при ударе вибрационное колебание идет вдоль тороидального тела в обе стороны, то если с одной стороны относительно точки удара, на расчетном расстоянии, равном длине волны, нанести дополнительный импульс с заранее заданной частотной характеристикой, то стартовавшая после первого удара продольная волна получит индивидуальные частотные характеристики – волновой маркер. Фиксируя при помощи приборов данную волну, многократно проходящую через регистрирующие датчики, возможно определить характеристики затухания волны с маркером, не учитывая встречную волную и ее интерференционные явления. Полноценная реализация этой гипотезы в древесине и других материалах, в том числе вновь создаваемых композитных и других, позволит точно определить их волновые характеристики, что может иметь важное прикладное значение.
Выводы
- В численном и натурном экспериментах выявлена закономерность, подтвердившая ранее сформулированную гипотезу о значительном превышении значения волны напряжения над величиной напряжения в состоянии покоя нагруженного элемента.
- При сжатии образца выявлен эффект колебания волны напряжения отражения, амплитуда которой устанавливается относительно значения напряжения в состоянии покоя. Минимальное значение напряжения близко к нулю, максимальное значение сопоставимо с удвоенным значением напряжения покоя.
- В окрестностях точки, находящейся на границе раздела сред, в приопорной части образца, разница между пиковыми значениями напряжений волны сжатия, которые волна проходит за весьма короткий промежуток времени, будет в значительной степени сокращать длительную прочность древесины.
Список литературы
1. <i>Кольский Г.</i> Волны напряжений в твердых телах. Москва: Изд-во иностр. лит-ры; 1955.
2. <i>Дейвис Р.М</i>. Волны напряжений в твердых телах. Москва: Изд-во иностр. лит-ры; 1961.
3. <i> Работнов Ю.Н.</i> Механика деформируемого твердого тела. 2-е изд. Москва: Наука; 1988.
4. <i>Романов П.Г., Сивцев П.В.</i> Численное моделирование волновых проявлений сопротивления деревянного образца с идеализированной анизотропией упругих параметров. Строительная механика и расчет сооружений. 2020;(1):37–43.
5. <i>Romanov P.G., Sivtsev P.V.</i> Features of the deformation of cross-glued wooden panel structures for northern construction. IOP Conference Series: Earth and Environmental Science. 2021;625(1):012018. https://doi.org/10.1088/1755-1315/625/1/012018.
6. <i>Romanov P.G., Sivtsev P.V.</i> Features of modeling of stress and strain waves in an anisotropic medium on the example of a wooden element. Journal of Physics: Conference. 2021;2131(3):032089. https://doi.org/10.1088/1742-6596/2131/3/032089.
7. <i>Романов П.Г. Сивцев П.В.</i> Численный эксперимент по испытаниям на сдвиг перекрестно-склеенного деревянного элемента. Строительная механика и расчет сооружений. 2023;306(1):56–64. https://doi.org/10.37538/0039-2383.2023.1.56.64.
8. <i>Sivtsev P.V., Romanov P.G.</i> Numerical modeling of deformation of cross-glued pine wood samples. AIP Conference Proceedings. 2022;2528(1):020017. https//doi.org/10.1063/5.0106881.
9. <i>Romanov P.G., Sivtsev P.V.</i> Visualization of deformation and stress waves in wooden solid and glued elements of building structures. Scientific Visualization. 2024;16(1):95–104. https://doi.org/10.26583/sv.16.1.08.
10. <i>Романов П.Г.</i> Численное моделирование напряженно-деформированного состояния узла соединения ДПК-панелей. Строительная механика и расчет сооружений. 2025;(1):2–8. https://doi.org/10.37538/0039-2383.2025.1.2.8.
Об авторах
П. Г. РомановРоссия
Прокопий Георгиевич Романов*, канд. техн. наук, доцент кафедры «Проектирование, строительство
и технологии» инженерно-технического института, Северо-Восточный федеральный университет
им. М.К. Аммосова, Якутск
ул. Белинского, д. 58, г. Якутск, 677000, Республика Саха (Якутия), Российская Федерация
e-mail: pg.romanov@mail.ru
А. А. Слепцов
Россия
Александр Александрович Слепцов, преподаватель-исследователь, Северо-Восточный федеральный университет им. М.К. Аммосова, Якутск
ул. Белинского, д. 58, г. Якутск, 677000, Республика Саха (Якутия), Российская Федерация
Рецензия
Для цитирования:
Романов П.Г., Слепцов А.А. Эффекты при отражении волны напряжений в деревянных образцах. Вестник НИЦ «Строительство». 2025;47(4):132-143. https://doi.org/10.37538/2224-9494-2025-4(47)-132-143. EDN: SMJSPD
For citation:
Romanov P.G., Sleptsov A.A. Effects of stress wave reflection in wooden samples. Bulletin of Science and Research Center of Construction. 2025;47(4):132-143. (In Russ.) https://doi.org/10.37538/2224-9494-2025-4(47)-132-143. EDN: SMJSPD
JATS XML


























