Перейти к:
Современные анизотропные критерии и предельные поверхности прочности каменной кладки при плоском напряженном состоянии для расчета в программных комплексах
https://doi.org/10.37538/2224-9494-2024-4(43)-232-245
EDN: BZOOMP
Аннотация
Введение. Для оценки прочности элементов пространственных несущих конструкций при автоматизированном расчете с использованием теории пластического течения необходимо задаться условием прочности, геометрическая интерпретация которого является поверхностью в пространстве напряжений. Выход точки, изображающей напряженное состояние, за пределы описанной поверхности в процессе нагружения расчетной модели означает разрушение материала. Для оценки прочности конструкций из каменных кладок необходимо учитывать особенности материала, такие как разносопротивляемость, зависимость прочности от угла анизотропии, различные значения двухосной прочности, что накладывает ограничение на использование существующих предельных поверхностей.
Цель. Обзор существующих критериев прочности, описание их преимуществ и недостатков, а также границ применимости для прочностного моделирования элементов конструкций из каменной кладки.
Материалы и методы. Обзор существующих критериев прочности проводится на актуальных источниках. Для оценки точности аппроксимации условий прочности экспериментальных данных, полученных при испытаниях, используются численные методы, реализованные на языке Python с использованием библиотек Numpy, Sympy, а также MatplotLib для графической визуализации полученных результатов. Теория тензорного исчисления используется для описания действующего и предельного напряженного состояния в элементарной точке конструкции, а аспекты линейной алгебры – для записи соотношений механических констант материала.
Результаты. Получена оценка точности аппроксимации экспериментальных данных критерием прочности Willam – Warnke в сравнении с критерием прочности Гениева для плоского напряженного состояния каменной кладки. В статье приводится краткий обзор существующих моделей прочности кладки с описанием их физических интерпретаций и применяемых подходов.
Выводы. Существующие критерии прочности имеют недостатки, такие как неточность аппроксимации экспериментальных данных, сложность реализации компьютерных расчетов, неполное описание прочностных свойств, феноменологичность используемых подходов. Актуальна разработка нового специализированного критерия для полноценного описания модели прочности каменной кладки.
Ключевые слова
Для цитирования:
Смагин И.В., Лихачева С.Ю., Поздеев М.Л. Современные анизотропные критерии и предельные поверхности прочности каменной кладки при плоском напряженном состоянии для расчета в программных комплексах. Вестник НИЦ «Строительство». 2024;43(4):232-245. https://doi.org/10.37538/2224-9494-2024-4(43)-232-245. EDN: BZOOMP
For citation:
Smagin I.V., Likhacheva S.Yu., Pozdeev M.L. Modern anisotropic criteria and limiting surfaces of masonry strength under plane stress state for calculations in software packages. Bulletin of Science and Research Center of Construction. 2024;43(4):232-245. (In Russ.) https://doi.org/10.37538/2224-9494-2024-4(43)-232-245. EDN: BZOOMP
Введение
Современная тенденция моделирования работы конструкций из каменных кладок подразумевает отход от эмпирических упрощенных моделей и использование механики деформируемого твердого тела. Такие материалы, как бетон и каменная кладка, имеют ярко выраженные псевдопластические механические свойства, таким образом, для оценки работы данных материалов нельзя использовать линейные модели классической теории упругости. Из наиболее эффективных и популярных подходов к моделированию таких конструкций стоит выделить деформационную теорию пластичности и теорию течения, которые позволяют вести расчет геометрически сложных и неоднородных по напряженному состоянию тел. Реализовать данный подход можно как для плоского, так и для объемного напряженный состояний.
Для проверки условия прочности в обозначенных выше теориях используются критерии, которые выделяют из множества возможных напряженных состояний в произвольной точке тела такое подмножество, при котором происходит разрушение материала. Геометрическая интерпретация этого условия представляет собой непрерывное множество точек, изображающих напряженное состояние в аффинном пространстве главных или пространстве нормальных и касательных напряжений к заданной площадке. Оно изображается объемной поверхностью или кривой для случая плоского напряженного состояния. Данная поверхность делит множество всех напряженных состояний в точке тела на два подмножества – приводящие и не приводящие к разрушению материала. Эти поверхности могут называться фигурами прочности, поверхностями предельного состояния или разрушения.
Для точного моделирования прочности элементов конструкций необходимо учитывать физические свойства материала. Каменная кладка имеет ярко выраженную разносопротивляемость в силу несимметричности относительно осей анизотропии периодически повторяющейся структуры [1], что должно находить отражение в асимметричности используемых фигур прочности. Этот факт также оказывает влияние на прочность при повороте осей главных напряжений в процессе нагружения расчетной модели каменной кладки. При повышении прочности раствора возрастает двухосная прочность элементов такой конструкции, что также необходимо учитывать при выборе критерия прочности. Как и в случае с бетонами, при объемном напряженном состоянии, при возрастании величины первого инварианта тензора действующих напряжений, каменная кладка показывает упрочнение, что должно моделироваться увеличением размера девиаторного сечения вдоль гидростатической оси в фигурах прочности каменной кладки. Для корректной оценки прочности необходимо использовать критерии, учитывающие величину отношения первого инварианта тензора действующих напряжений ко второму. Это означает невозможность использования классических критериев прочности Треска, Мизеса или критериев прочности для композитов аналогичных критерию Tsai – Wu [2] для описания свойств трехосного напряженного состояния. Кроме того, фигура прочности должна быть искривлена вдоль меридиональных сечений.
Зависимость значений прочности от направления силового воздействия
При моделировании работы каменной кладки используется подход, описанный в работах, посвященных однонаправленным композитным материалам [3][4]. В рамках данного подхода вдоль и перпендикулярно постельным швам кладки вводятся оси анизотропии и параметр ϴ – угол между осями анизотропии и осями главных напряжений. Принимается, что оси анизотропии также ортогональны. Фиксируются значения одноосных прочностей вдоль данных осей, а промежуточные значения прочности на площадках главных напряжений получаются исходя из направления их действия относительно осей анизотропии (рис. 1). Для плоского напряженного состояния соотношения преобразований главных напряжений в напряжения, действующие по осям анизотропии, имеют следующую запись в матричной форме:
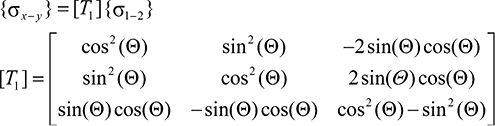 . (1)
. (1)
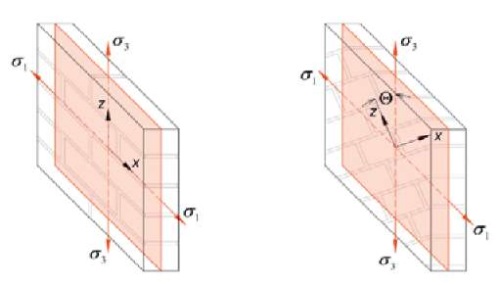
Рис. 1. Схема поворота осей напряжений каменной кладки
Fig. 1. Diagram of stress axis rotation in masonry
Используя представленный подход, поверхности прочности должны перестраиваться в процессе нагружения расчетной макромодели. Каждый критерий прочности имеет различный характер изменения величины предельного сопротивления при смене осей главных напряжений, что необходимо учитывать при выборе оптимальной модели.
Для оценки качественного характера изменения предельной осевой прочности можно использовать следующую методику. К однонаправленному композиту (рис. 2) прикладывается эквивалентная предельная нагрузка, вызывающая напряжения по осям анизотропии, приводящая к нарушению условия прочности на этих осях. При смене значения угла ϴ значение предельной осевой прочности будет меняться. Так может быть получено условие изменения разрушающей нагрузки разносопротивляющегося материала от угла ϴ (рис. 2).
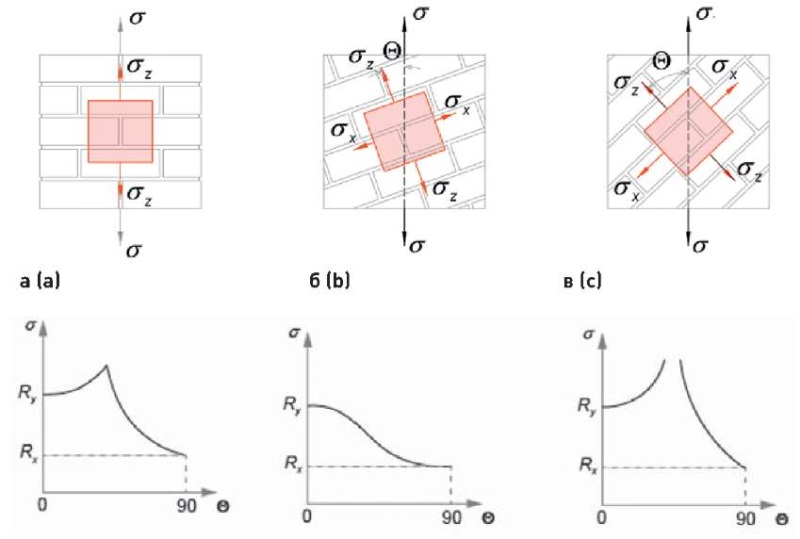
Рис. 2. Зависимость предельной осевой прочности от угла анизотропии для критериев прочности: а – критерий наибольших нормальных напряжений; б – эллиптический критерий прочности; в – критерий Кулона – Мора
Fig. 2. Dependence of ultimate axial strength on the angle of anisotropy for strength criteria: a – maximum normal stress criterion; b – elliptical strength criterion; c – Coulomb-Mohr criterion
Критерии прочности, геометрическая интерпретация которых в пространстве действующих напряжений описывается линией, условно называемые линейными критериями прочности, показывают на графике зависимости предельной осевой прочности от угла ϴ нарушения условий гладкости и непрерывности функции, что может оказывать влияние при компьютерном расчете элементов конструкции.
Для изображения всего множества напряженных состояний в точке, приводящих к разрушению, с учетом влияния угла анизотропии можно использовать величины касательных (τxy) и нормальных (σx, σy) напряжений, действующих в кладке, или работать в терминах главных напряжений (σ1, σ2) и угла наклона максимального главного напряжения к постели кладки ϴ. Эти варианты построения приведены на примере критерия кладки Гениева – Воронова (рис. 3) [5].
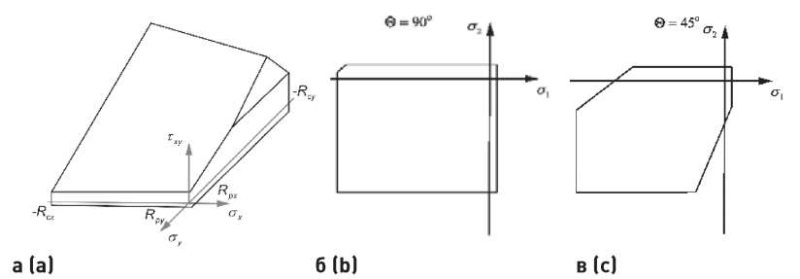
Рис. 3. Критерий прочности Гениева – Воронова: а – в терминах касательных и нормальных напряжений; б, в – в терминах главных напряжений и угла ϴ
Fig. 3. Geniev – Voronov strength criterion: a – in terms of shear and normal stresses; b, c – in terms of principal stresses and angle ϴ
Критерии прочности при плоском напряженном состоянии
В целом любые критерии могут быть выражены через одно условие или комбинацию различных условий прочности. Так, например, критерий прочности Хоффмана [6] описывается единой формулой (2). Его геометрическая интерпретация в пространстве главных напряжений является замкнутой кривой второго порядка.
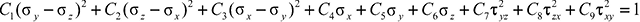 , (2)
, (2)
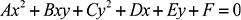 . (3)
. (3)
Стоит отметить, что каноническое уравнение второго порядка (3) имеет всего пять несвободных членов, влияющих на форму фигуры прочности, и один свободный, отвечающий за «масштабирование» фигуры. Для моделирования прочности каменных конструкций при плоском напряженном состоянии необходимо использовать минимум шесть параметров, влияющих на форму фигуры, а именно: четыре параметра на фиксирование одноосных прочностей при сжатии и растяжении и два параметра для моделирования двухосной прочности. Следовательно, невозможно в полной мере использовать эллиптические критерии для моделирования прочности элементов конструкций из каменных кладок, что и замечает автор в работе [7]: ни при ручном подборе параметров, ни при поиске подходящих значений коэффициентов методом наименьших квадратов не получается получить удовлетворительный результат.
Существуют попытки использовать кривые третьего порядка, например в работе [8]. При таком подходе возникают сложности в силу нарушения условия замкнутости фигуры прочности. В таких случаях необходимо пересчитывать коэффициенты для уравнения по известной методике, используя частные производные. Это усложняет возможность использования данных критериев для компьютерного расчета каменных кладок, поскольку при сложном нагружении фигура должна перестраиваться вместе с изменением угла анизотропии, следовательно на каждом шаге итераций необходимо предусмотреть проверку условия замкнутости, что приводит к кратному повышению сложности алгоритма расчета конструкции, особенно при использовании теории течения.
В случае использования комбинации различных условий прочности существуют свои преимущества и недостатки. Классическим примером таких критериев для каменных кладок является модель прочности Ganz [9]. Эта модель выделяет пять режимов разрушения, что полезно при анализе результатов расчета, дает четкое понимание причины возможного разрушения элементов конструкции, но совокупность большого количества используемых поверхностей уменьшает эффективность их реализации в теории пластического течения. Существуют и более эффективные феменологические модели, которые нашли свое применение для компьютерного расчета. Например, модель Lourenco [10], используемая в программном комплексе DIANA FEA, содержит в себе только две поверхности прочности, что значительно упрощает процесс моделирования элементов конструкций из каменных кладок.
Объемное напряженное состояние
Условия разрушения при объемном напряженном состоянии предпочтительно записывать в координатах Хейга – Вестергаарда. Для этого симметричный тензор второго порядка, изображающий напряженное состояние в точке тела σ, следует представить в виде разложения на шаровый тензор n и девиатор s:
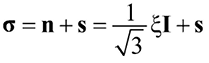 ,
,
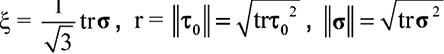 . (4)
. (4)
Тензор n изображает напряжение, действующее на октаэдрической площадке, нормаль которой ра́вно наклонена к осям главных напряжений (т. е. результирующая площадка), а s – напряжение, действующее на этой площадке (рис. 4).
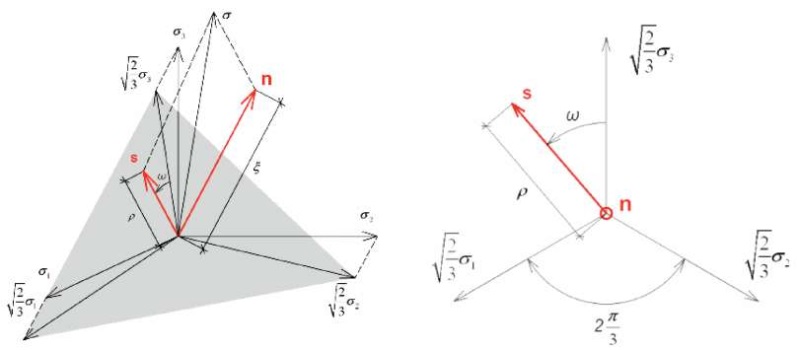
Рис. 4. Графическая интерпретация разложения тензора напряжений в пространстве главных напряжений и на девиаторной плоскости
Fig. 4. Graphical interpretation of the stress tensor decomposition in principal stress space and on the deviatoric plane
Напряженное состояние в каждой точке тела можно представить как равномерное всестороннее растяжение или сжатие, на которое наложено напряженное состояние сдвига, определяемое девиатором. Компоненты шарового тензора стремятся изменить объем элемента тела, а компоненты девиатора – изменить форму этого элемента без изменения объема. Разложив полученную зависимость на базисы, направленные вдоль проекции осей главных напряжений на результирующую площадку, получим следующую запись действующих главных напряжений (5) [11]:
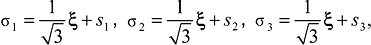 (5)
(5)
где
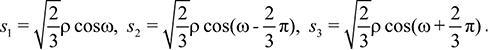
Для описания прочности при трехосном напряженном состоянии можно взять за основу объемную фигуру прочности Гениева [12]. Данный критерий прочности состоит из комбинации двух условий – условия прочности на срез и раздробления (рис. 5). В данном критерии считается, что потеря прочности на срез происходит за счет скольжения на некоторых произвольных площадках. Прочность сдвига на этих площадках будет увеличиваться за счет действия нормальных напряжений сжатия.
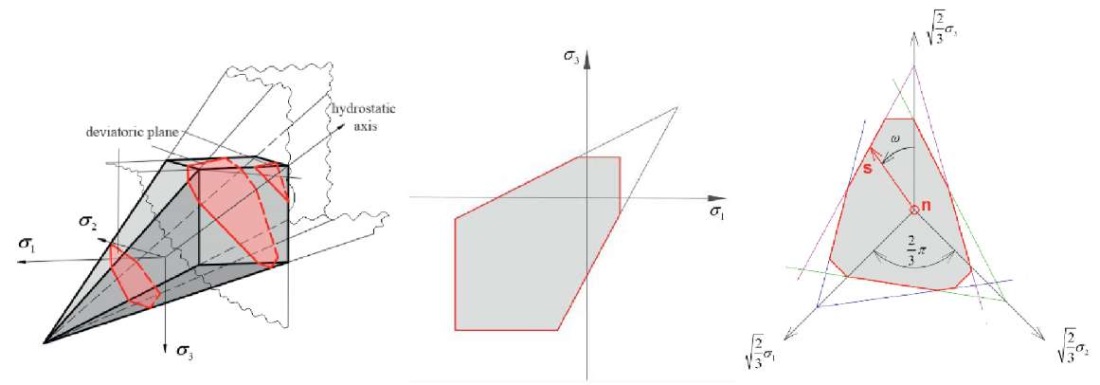
Рис. 5. Объемный критерий прочности Гениева в пространстве главных напряжений и на девиаторной площадке
Fig. 5. Volumetric Geniev strength criterion in principal stress space and on the deviatoric plane
Также при разработке критерия наложено условие, определяющее возможность дислокаций только на площадках, перпендикулярных к осям анизотропии. Конечный поиск таких площадок является оптимизационной задачей, решение которой находится численными методами или аналитически, используя, например, метод Лагранжа:
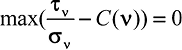 , (6)
, (6)
где C (ν) – закон изменения прочности на сдвиг;
τν – касательное напряжение на площадке сдвига;
σν – нормальное напряжение на площадке сдвига.
Таким образом, критерий прочности моделирует физический процесс потери прочности каменной кладки на срез. Условие прочности при раздроблении описывается анизотропным критерием прочности Ренкина для трехосного напряженного состояния.
Область допустимых напряжений данного критерия ограничена поверхностями прямоугольного параллелепипеда и шестигранной неправильной пирамиды. В девиаторном сечении данная фигура имеет вид неправильного многоугольника (рис. 5).
Данный критерий не учитывает увеличения двухосной прочности каменной кладки при сжатии вследствие увеличения прочности используемого раствора. Главным недостатком такого критерия при численном моделировании будет высокая алгоритмическая сложность расчета конструкций ввиду необходимости решения оптимизационной задачи поиска площадок скольжения на каждом шаге итерационного расчета. Вероятно, описанный подход стоит использовать для единичных научных расчетов, не требующих высокой скорости выполнения.
Популярным случаем моделирования каменной кладки является использование критериев прочности для бетона [13], например критерия William – Warnke [14]. Существует трехпараметрическая модель William – Warnke (WW-3), которая представляет собой коническую поверхность разрушения с криволинейным сечением в девиаторной плоскости. Прочность в таком варианте критерия зависит как от гидростатического, определяющегося первым инвариантом тензора действующих напряжений, так и от девиаторного напряженного состояния. Также существует и пятипараметрическая модель с криволинейными меридиональными сечениями. Первая модель более простая в аналитической реализации и удачно описывает случаи напряженного состояния с низкими значениями первого инварианта тензора действующих напряжений, а вторая – с высокими. Пятипараметрический критерий William – Warnke однозначно определяется через несколько механических констант, а именно: предел прочности при одноосном сжатии, предел прочности при одноосном растяжении, предел прочности при двухосном сжатии, значение крайней точки напряжения на меридиане растяжения, значение крайней точки напряжения на меридиане сжатия.
Данная модель описывает прочность элементов каменных конструкций недостаточно точно. Это наглядно видно при наложении трехпараметрической модели на экспериментальные точки, полученные по результатам испытаний Пейджа [15] (рис. 6 и 7). Сравнение качества аппроксимации данного критерия со специализированным критерием для каменных кладок Гениева при плоском напряженном состоянии показывает существенное преимущество второго.
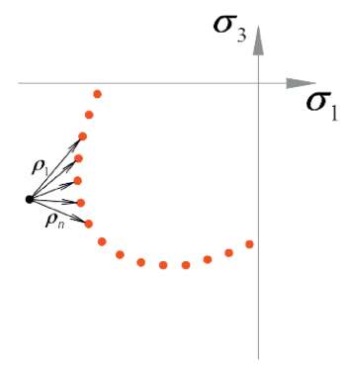
Рис. 6. К определению качества аппроксимации экспериментальных данных
Fig. 6. Determining the quality of experimental data approximation
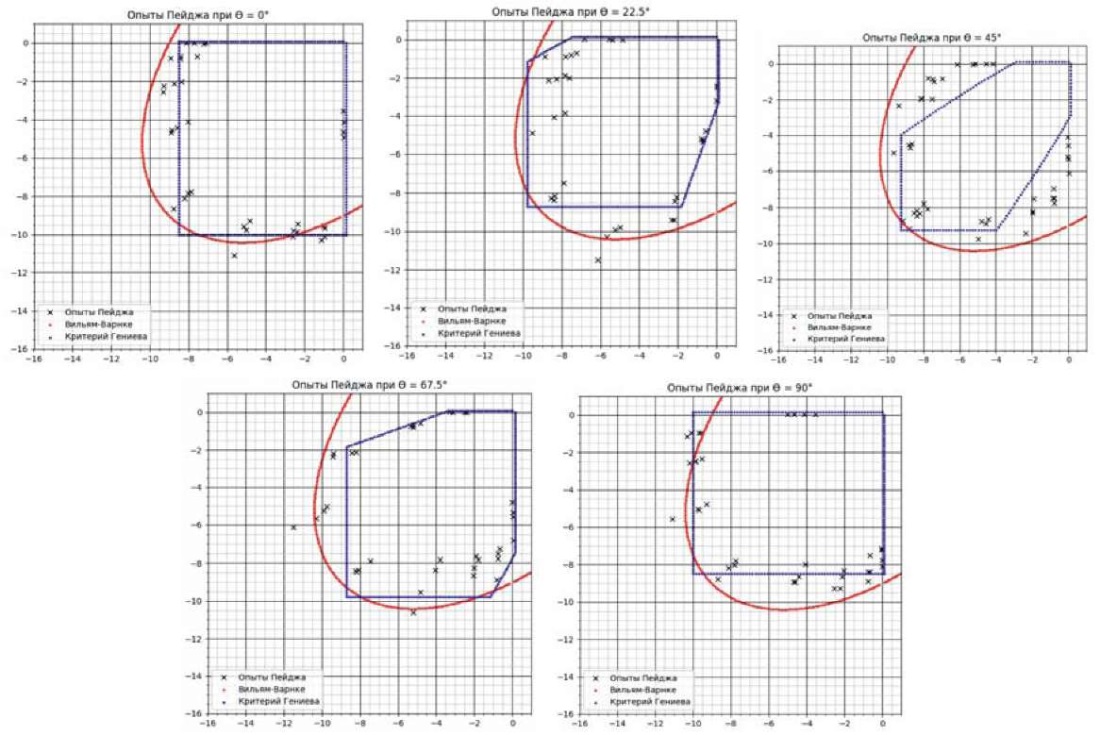
Рис. 7. Критерии прочности Гениева и William – Warnke на точках испытаний Пейджа
Fig. 7. Geniev and Willam – Warnke strength criteria at Page test points
Для сравнения качества аппроксимации этих критериев была использована следующая методика. Выделим точки, лежащие на геометрической интерпретации изучаемых критериев. Будем называть такие точки аналитическими, важно, чтобы они были распределены по фигуре равномерно. Далее возьмем экспериментальную точку и будем искать расстояние от нее до каждой аналитической точки:
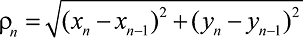 . (7)
. (7)
Значение минимального расстояния будем считать расстоянием от экспериментальной точки до исследуемой фигуры. Выполним те же действия для каждой экспериментальной точки и получим сумму всех найденных расстояний. Качество аппроксимации будет характеризоваться величиной этого значения: чем оно меньше, тем лучше фигура описывает экспериментальные точки.
Значения отклонений от результатов экспериментов Пейджа у специализированного критерия Гениева для плоского напряженного состояния меньше, чем у критерия William – Warnke, что показано в табл. 1. В первую очередь это объясняется отсутствием возможности перестроения WW-3 в зависимости от угла ϴ и невозможностью учета разносопротивляемости кладки при плоском напряженном состоянии. Наименьшая относительная погрешность получается при угле 45 градусов, когда экспериментальные точки ложатся симметрично относительно проекции гидростатической оси на плоскость главных напряжений.
Таблица 1
Результаты оценки качества аппроксимации экспериментальных точек опытов Пейджа
Тable 1
Results of assessing the quality of approximation for Page test points
|
Критерий прочности |
Отклонения от результатов опытов Пейджа при угле ϴ, град. |
||||
|
0 |
22,5 |
45 |
67,5 |
90 |
|
|
Критерий Гениева |
12,32 |
24,63 |
40,14 |
25,62 |
12,06 |
|
Критерий William – Warnke |
46,64 |
67,01 |
73,87 |
70,49 |
41,73 |
|
Относительная погрешность, % |
73,58 |
63,24 |
45,66 |
63,65 |
71,10 |
Обсуждение
Существует множество подходов к описанию прочности элементов конструкций. У каждого подхода есть свои преимущества и недостатки: некоторые дают точное описание модели разрушения и описывают физику процесса, но не подходят для построения эффективных алгоритмов в силу сложности и многоэтапности построения фигуры прочности, другие, напротив, эффективны в построении, но требуют серьезной предварительной проработки экспериментальной базы. Для каждой цели должен использоваться свой инструмент. Например, громоздкий на первый взгляд и не самый современный критерий прочности Ganz по-прежнему используется в исследованиях [16]. С некоторой модификацией этот критерий калибруется для описания модели размазанных трещин. Вероятно, в таких задачах исследователю удобно использовать такую модель, в которой известно, в каком элементе композита возникла трещина. Тем не менее для простого инженера такая информация может быть излишней, решением его проблем будет простой перебор механических параметров раствора и камня в кладке.
Известно много попыток создать специализированный критерий прочности каменной кладки, тем не менее на данный момент не существует удовлетворительной модели. В случае плоского напряженного состояния следует выделить модель Lourenco и его подход к составлению объединенной фигуры из минимального числа стыкуемых поверхностей. Например, доработав критерий прочности Hoffman и получив аналитические зависимости двухосной прочности от прочности раствора на срез, получится построить простую и эффективную в алгоритмизации модель. Для трехосного напряженного состояния на данный момент развитие механики деформирования твердого тела для каменной кладки находится на этапе заимствования моделей других материалов – будь то общие модели для материалов, обладающих внутренним трением, или специализированные модели для бетона. Вероятно, доработка и увязка коэффициентов математических зависимостей с механическими характеристиками каменной кладки одного из таких критериев, например [17][18], будет показывать хорошую реализацию в алгоритмах численных расчетов.
Заключение
Рассмотрены различные критерии прочности: Hoffman, Tsai – Wu, Ganz, Lourenco, Syrmakezis and Asteris, Bilko – Małyszko, William – Warnke, критерии прочности кладки Гениева для объемного и плоского напряженного состояния. Описана их применимость для моделирования работы каменных кладок. Приведены методики описания прочностей, свойств каменной кладки, необходимые для учета в расчетных моделях. Разработана методика оценки точности аппроксимации. Получена оценка точности аппроксимации экспериментальных данных Пейджа критерием прочности Willam – Warnke в сравнении с критерием прочности Гениева для плоского напряженного состояния.
Список литературы
1. <i>Капустин С.А., Лихачева С.Ю</i>. Моделирование процессов деформирования и разрушения материалов с периодически повторяющейся структурой. Нижний Новгород: ННГАСУ; 2012.
2. <i>Tsai S. W., Wu E.M</i>. A General Theory of Strength for Anisotropic Materials. Journal of Composite Materials. 1971;5(1):58–80. https://doi.org/10.1177/002199837100500106
3. <i>Вишняков Л.Р., Грудина Т.В., Кадыров В.Х</i>. Композиционные материалы: справочник. Киев: Наукова думка; 1985.
4. <i>Полилов А.Н</i>. Этюды по механике композитов. Москва: Физико-математическая литература; 2015.
5. <i>Воронов А.Н</i>. Статические плоские задачи деформационной теории пластичности ортотропных тел [диссертация]. Москва; 1984.
6. <i>Hoffman O</i>. The Brittle Strength of Orthotropic Materials. Journal of Composite Materials. 1967;1(2):200–206. https://doi.org/10.1177/002199836700100210
7. <i>Lourenco P.J.B.B</i>. Computational strategies for masonry structures [dissertation]. Delft University Press; 1996.
8. <i>Syrmakezis C.A., Asteris P.G</i>. Masonry Failure Criterion under Biaxial Stress State. Journal of Materials in Civil Engineering. 2001;13(1):58–64. https://doi.org/10.1061/(asce)0899-1561(2001)13:1(58)
9. <i>Ganz H.R</i>. Mauerwerksscheiben unter normalkraft und schub [PhD Thesis]. ETH Zurich; 1985.
10. <i>Lourenco P.B</i>. An orthotropic continuum model for the analysis of masonry structures [Report]. The Netherlands, TU Delft; 1995.
11. <i>Małyszko L., Jemioło S., Bilko P., Gajewski M</i>. MES i modelowanie konstytutywne w analizie zniszczenia konstrukcji murowych. Olsztyn: Wydawnictwo Uniwersytetu Warmińsko-Mazurskiego; 2015.
12. <i>Гениев Г.А., Курбатов А.С., Самедов Ф.А</i>. Вопросы прочности и пластичности анизотропных материалов. 1993.
13. <i>Drobi ec L., Šlivinskas T</i>. Determination of mortar and brick failure surface based on research in a complex state of stress. Materiały Budowlane. 2016;(12):42–44. https://doi.org/10.15199/33.2016.12.13
14. <i>Willam K.J., Warnke E.P</i>. Constitutive model for the triaxial behavior of concrete. Proceedings of IABSE, Structural Engineering. 1975;19:1–30.
15. <i>Page A.W</i>. The biaxial compressive strength of brick masonry. Proceedings of the Institution of Civil Engineers. 1981;71(3):893–906. https://doi.org/10.1680/iicep.1981.1825
16. <i>Plizzari G., Vecchio F.J</i>. Fiber reinforced concrete and mortar for enhanced structural elements and structural repair of masonry walls [Ph.D. Thesis]. University of Brescia, Italy; 2012.
17. <i>Bigoni D., Piccolroaz A</i>. Yield criteria for quasibrittle and frictional materials. International journal of solids and structures. 2004;41(11–12):2855–2878. https://doi.org/10.1016/j.ijsolstr.2003.12.024
18. <i>Piccolroaz A., Bigoni D</i>. Yield criteria for quasibrittle and frictional materials: a generalization to surfaces with corners. International Journal of Solids and Structures. 2009;46(20):3587–3596. https://doi.org/10.1016/j.ijsolstr.2009.06.006
Об авторах
И. В. СмагинРоссия
Илья Васильевич Смагин*, аспирант кафедры теории сооружений и технической механики, ННГАСУ, Нижний Новгород
ул. Ильинская, д. 65, г. Нижний Новгород, 603000, Российская Федерация
e-mail: ivsmag@vk.com
С. Ю. Лихачева
Россия
Светлана Юрьевна Лихачева, канд. физ.-мат. наук, доцент, профессор кафедры теории сооружений и технической механики, ННГАСУ, Нижний Новгород
ул. Ильинская, д. 65, г. Нижний Новгород, 603000, Российская Федерация
e-mail: lihsvetlana@yandex.ru
М. Л. Поздеев
Россия
Максим Леонидович Поздеев, аспирант кафедры теории сооружений и технической механики, ННГАСУ, Нижний Новгород; инженер-исследователь, ООО «Автоматизация проектных работ» (ГК «SCAD Soft»), Москва
ул. Ильинская, д. 65, г. Нижний Новгород, 603000, Российская Федерация; Рубцовская наб., д. 4, к. 1, помещ. VII, г. Москва, 105082, Российская Федерация
e-mail: pm@scadsoft.ru
Рецензия
Для цитирования:
Смагин И.В., Лихачева С.Ю., Поздеев М.Л. Современные анизотропные критерии и предельные поверхности прочности каменной кладки при плоском напряженном состоянии для расчета в программных комплексах. Вестник НИЦ «Строительство». 2024;43(4):232-245. https://doi.org/10.37538/2224-9494-2024-4(43)-232-245. EDN: BZOOMP
For citation:
Smagin I.V., Likhacheva S.Yu., Pozdeev M.L. Modern anisotropic criteria and limiting surfaces of masonry strength under plane stress state for calculations in software packages. Bulletin of Science and Research Center of Construction. 2024;43(4):232-245. (In Russ.) https://doi.org/10.37538/2224-9494-2024-4(43)-232-245. EDN: BZOOMP


























