Перейти к:
Квазиортотропная деформационная теория пластичности каменных кладок при плоском напряженном состоянии
https://doi.org/10.37538/2224-9494-2024-4(43)-218-231
EDN: CYKUXR
Аннотация
Введение. Деформационная теория пластичности (деформационная теория) может широко использоваться в физически нелинейных расчетах при простых или сходящихся к простым нагружениях. В частности, для анализа сейсмостойкости каменных зданий деформационная теория может быть использована в рамках нелинейного статического метода. При сравнении с теориями типа течения деформационные теории позволяют реализовать большее количество механизмов разрушения, задавая сложную объединенную фигуру прочности материала, не имея проблем с сингулярностью предельных поверхностей нагружения. Цель. Разработка варианта деформационной теории пластичности каменных кладок при плоском напряженном состоянии с учетом ортотропии прочностных свойств.
Материалы и методы. Проведен анализ известных деформационных теорий. Физические соотношения формулируются в матричном виде для использования в компьютерных расчетах. Сравнение математической модели с экспериментальными результатами производится методами регрессионного анализа.
Результаты. Описана деформационная теория каменных кладок как квазиортотропного материала без учета деформационной анизотропии. Предложена фигура прочности каменных кладок, учитывающая ортотропию прочностных свойств и зависящая от угла между главными осями и осями ортотропии. Описана методика трансформации двух базовых кривых деформирования каменных кладок.
Выводы. Описана квазиортотропная деформационная модель каменной кладки, которая может быть использована в программах МКЭ-анализа, а также в написании плагинов к уже имеющимся программным комплексам, в частности к программному комплексу SCAD Office c моделью деформационной теории пластичности.
Ключевые слова
Для цитирования:
Поздеев М.Л., Лихачева С.Ю., Смагин И.В. Квазиортотропная деформационная теория пластичности каменных кладок при плоском напряженном состоянии. Вестник НИЦ «Строительство». 2024;43(4):218-231. https://doi.org/10.37538/2224-9494-2024-4(43)-218-231. EDN: CYKUXR
For citation:
Pozdeev M.L., Likhacheva S.Yu., Smagin I.V. Quasi-orthotropic deformation theory of masonry plasticity in plane stress state. Bulletin of Science and Research Center of Construction. 2024;43(4):218-231. (In Russ.) https://doi.org/10.37538/2224-9494-2024-4(43)-218-231. EDN: CYKUXR
Введение
Выполнение расчетов каменных конструкций с учетом физической нелинейности при сложных напряженных состояниях является важной задачей обеспечения надежности зданий в рамках как реконструкции, так и нового строительства. Актуальность расчетов в условиях плоского напряженного состояния возрастает для строительства сейсмостойких зданий, каменные стены которых обеспечивают горизонтальную жесткость, а их нелинейное поведение под нагрузкой обеспечивает демпфирование и уменьшает сейсмическую реакцию конструктивной системы здания в целом.
В инженерной практике наиболее распространенным методом анализа сейсмостойкости является линейно-спектральный метод. В рамках этого метода рассматривается упругая работа системы, а уменьшение сейсмической нагрузки за счет нелинейных эффектов косвенно учитывается согласно СП 14.13330.2018 «СНиП II-7-81* Строительство в сейсмических районах» [1] коэффициентом допускаемых повреждений К1. В нормах европейского сообщества Eurocode 8 (EN 1998-1) [2] введен аналогичный коэффициент поведения q. Авторы работ [3][4] указывают на слабую обоснованность данного коэффициента, в частности в работе [3] отмечается его историческое изменение для каменных конструкций.
Использование нелинейных моделей материалов позволяет обосновать сейсмостойкость здания без использования косвенных коэффициентов. При анализе сейсмостойкости с учетом нелинейной работы материала в рамках деформационной теории может быть использован нелинейный статический метод (Pushover Analysis) [4]. При отсутствии цикличности в рамках метода реализуется простой тип нагружения, когда компоненты девиатора напряжений возрастают пропорционально одному параметру, что позволяет использовать для такого расчета предпосылки деформационной теории. Феноменологические подходы требуют большого представительного объема данных для анализа в отличие от микромоделей [5], однако более оптимальны для инженерного расчета зданий и сооружений. При сравнении с теориями типа течения [6][7] они позволяют реализовать большее количество механизмов разрушения, задавая сложную объединенную фигуру прочности материала, решая проблему сингулярности предельных поверхностей нагружения. В работе [8] использование деформационной теории бетона [9] для каменных кладок показало наилучшее соответствие с результатами эксперимента при уровнях нагружения 0,5–0,75 от предельной вертикальной силы, недооценив несущую способность при малых величинах обжатия, что говорит об актуальности совершенствования деформационной теории.
Основные гипотезы
Описанная в статье квазиортотропная деформационная теория для каменных кладок основана на работах [9–12]. Модель расширена на случай ортотропного материала в сравнении с [11][12] и учитывает дилатационные эффекты в отличие от [10]. В модели рассматривается обобщенное плоское напряженное состояние, то есть учитываются деформации из плоскости нагружения, возникающие за счет коэффициента поперечной деформации.
Для установления деформационных зависимостей выдвигается ряд гипотез:
– сдвиговая деформация на октаэдрических площадках γo является непрерывной нелинейной функцией октаэдрического касательного напряжения τo, вида напряженного состояния ξ и угла между главными напряжениями и осями ортотропии α;
– средняя деформация εo является непрерывной нелинейной функцией октаэдрического нормального (среднего) напряжения σo, вида напряженного состояния ξ и угла между главными напряжениями и осями ортотропии α;
– основные физические соотношения в начальной точке деформирования должны соответствовать закону Гука для линейно-упругого изотропного тела;
– предельная поверхность в осях главных напряжений и деформаций соответствует поверхности для ортотропного материала и является функцией вида напряженного состояния ξ (или ω, χ) и угла между главными напряжениями и осями ортотропии α.
Разрабатываемая модель не учитывает развитие деформационной анизотропии. Данный вопрос представляет особый интерес будущих исследований.
Обобщенный закон Гука для нелинейно-упругого тела
Введем ортогональную систему координат XYZ, такую, что направление оси X будет параллельно горизонтальным растворным швам кладки, а Y – параллельно вертикальным швам.
В работе [13] показано, что при статическом расчете каменных конструкций, кладка которых выполнена из керамического полнотелого и пустотелого (с пустотностью до 25 %) кирпича, ее деформационные характеристики следует принимать как для изотропных материалов.
Используя нотацию Фойгта, тензоры напряжений и деформаций могут быть представлены в виде шестимерных векторов σ и ε соответственно. Тогда обобщенный закон Гука для изотропного материала может быть записан в матричном виде:
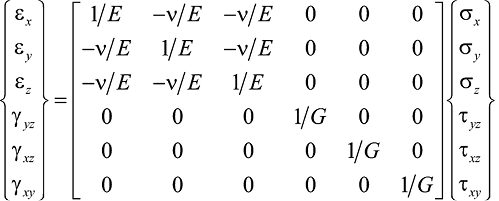 , (1)
, (1)
или в сокращенной форме:
ε = Sσ, (2)
где S – матрица податливости.
Поскольку в рамках деформационной теории решается задача о нелинейно-упругом теле, вместо постоянных параметров упругости, составляющих матрицу податливости, могут быть рассмотрены их секущие (редуцированные) значения, решая линейную задачу упругости на каждом шаге нагружения. При этом деформационные зависимости, характеризующие нелинейное поведение, определяются обобщенными кривыми деформирования τo – γo и σo – εo.
Действительные значения редуцированных технических характеристик (модуля деформации Ered и коэффициента поперечной деформации νred) могут быть выражены через известные значения (по зависимостям τo – γo и σo – εo) секущего модуля сдвига Gred = G0/ψ и секущего модуля объемной деформации Kred = K0/φ (рис. 1):
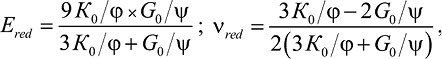 (3)
(3)
где ψ и φ – параметры пластичности, определяемые в следующем разделе статьи.
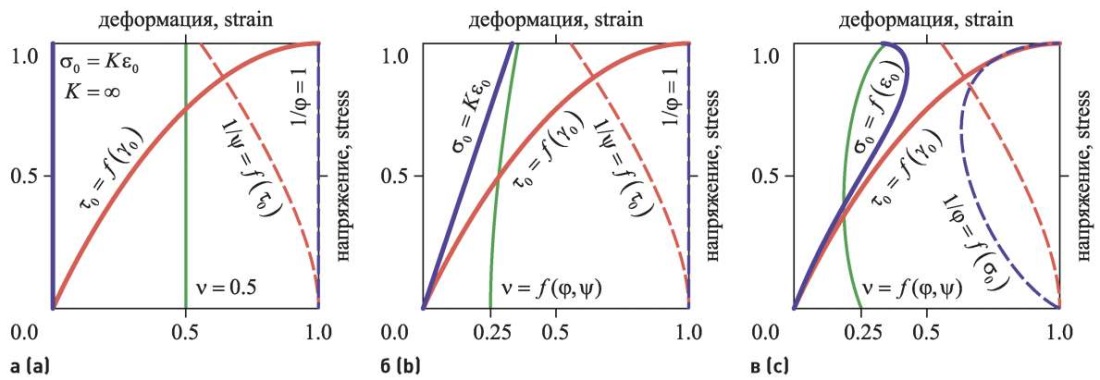
Рис. 1. Нелинейные зависимости к определению переменных параметров упругости: a – при K = ∞; б – при K = K0; в – при учете дилатации
Fig. 1. Nonlinear dependencies for determining variable elasticity parameters: a – at K = ∞; b – at K = K0; c – when considering dilatation
На рис. 1 в относительных координатах отражен характер изменения коэффициента поперечной деформации ν в процессе нелинейного деформирования в зависимости от вида обобщенных кривых τo – γo и σo – εo. При К = К0 = ∞ (рис. 1а) коэффициент ν = 0,5 при любом уровне напряжений, что соответствует поведению несжимаемого тела (модель каменной кладки Тюпина [10]), при К = const = К0 (рис. 1б) коэффициент ν нелинейно увеличивается вплоть до значения, равного 0,5. При учете дилатации (нелинейной зависимости σo – εo) (рис. 1в) коэффициент ν сначала нелинейно уменьшается, а затем возрастает также вплоть до значения 0,5.
Кривые деформирования
Для определения нелинейного поведения кладки в процессе нагружения в рамках рассматриваемой модели требуется задание двух обобщенных кривых деформирования: τo – γo и σo – εo (гипотезы 1 и 2 соответственно), затем определение функциональных зависимостей для параметров пластичности ψ и φ.
Для учета разупрочнения материала требуется задание кривых с ниспадающей ветвью. В работе [14] приведен обзор известных зависимостей σ – ε для случая одноосного сжатия кладочных образцов. Можно выделить два типа диаграмм: трех- и пятипараметрические. Поведение ветви разупрочнения трехпараметрической диаграммы определяется соотношением начального E0 и секущего в предельном состоянии Eu модулей. В работе [14] показана хорошая корреляция такой зависимости с экспериментальными данными для кладки из бетонных блоков.
В работе [15] на основе экспериментальных исследований [16] показано, что на постпиковое поведение кирпичной кладки влияет вид используемого раствора, так образцы с добавками извести показали более пластическое поведение. Для более точного задания ниспадающей зависимости может использоваться пятипараметрическая диаграмма, приведенная в работе [15].
При построении зависимости τo – γo использовано трехпараметрическое уравнение вида (рис. 2):
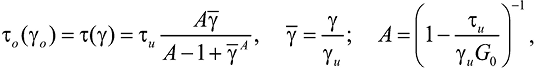 (4)
(4)
где G0 – начальный модуль сдвига;
τu – предельное октаэдрическое касательное напряжение;
γu – предельная октаэдрическая сдвиговая деформация.
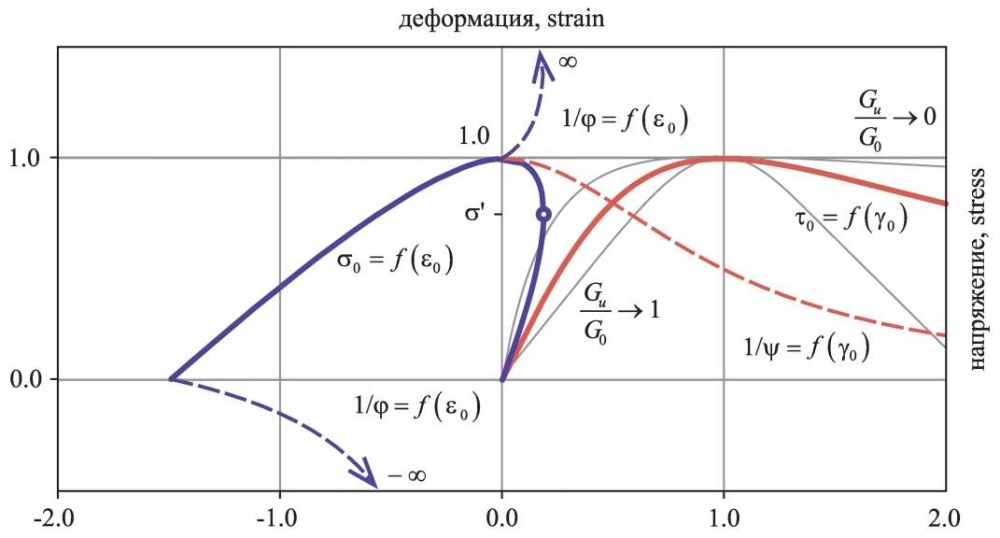
Рис. 2. Кривые деформирования τo – γo и σo – εo, функции параметров пластичности ψ и φ
Fig. 2. Deformation curves τo – γo and σo – εo, functions of plasticity parameters ψ and φ
Уравнение (4) позволяет получить требуемый характер постпикового поведения кладки в области растяжения и сжатия. Так, при стремлении отношения Gu/G0 к единице (рис. 2) разрушение имеет хрупкий характер, что характерно для работы кладки при растяжении; при уменьшении данного соотношения разрушение имеет более выраженный пластический характер, как при работе кладки на сжатие.
Каменная кладка является дилатирующим материалом, на что указывают экспериментальные исследования, например в работе [17] приведены нелинейные зависимости осевого напряжения как функции объемной деформации. Введем условие, согласно которому в предельном состоянии коэффициент поперечной деформации ν достигает значения 0,5, что соответствует значению объемного модуля деформации K = ∞, тогда нелинейная зависимость σo – εo может быть представлена в виде (рис. 2):
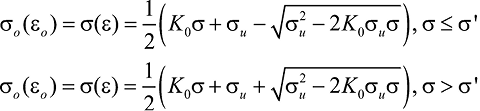 , (5)
, (5)
где K0 – начальный объемный модуль упругости;
σu – предельное октаэдрическое нормальное напряжение;
σ′ = 3σu/4 – напряжение макротрещинообразования.
Для описанных кривых деформирования могут быть определены функциональные зависимости (рис. 1):
параметр пластичности по сдвиговым деформациям:
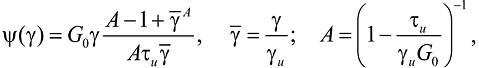 (6)
(6)
параметр пластичности по объемным деформациям:
 (7)
(7)
Вид кривых ψ и φ зависит от значений следующих переменных характеристик, выражаемых как функции нескольких переменных:
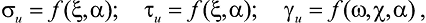 (8)
(8)
где α – угол между главными напряжениями и осями ортотропии;
ξ = σo/τo – параметр вида напряженного состояния;
ω, χ – параметры вида деформационного состояния.
Для описания функциональных зависимостей (8) требуется задание предельной кривой прочности (фигуры прочности) в осях главных напряжений и предельной поверхности в осях главных деформаций.
Фигура прочности каменной кладки в осях главных напряжений
Фигура прочности каменной кладки может быть описана системой уравнений, ограничивающей область допускаемых напряжений в пространстве главных напряжений.
Фигура прочности базируется на экспериментальных исследованиях [18, 19], выполненных на образцах из керамических кирпичей, и не учитывает увеличение двухосной прочности кладки при повышении относительной прочности раствора в современных кладках [20].
В работе [21] в области двухосного сжатия (C1, C3 на рис. 3) и растяжения (T1, T3 на рис. 3) фигура прочности кладки принимается по теории максимальных нормальных напряжений. Компоненты вектора предельного напряжения в главных осях при сжатии Rc,31 = (Rc3, Rc1)T и растяжении Rt,31 = (Rt3, Rt1)T для заданного напряженного состояния выражаются через предельные напряжения в осях ортотропии Rc, uv = (Rcu, Rcv)T и Rt, uv = (Rtu, Rtv)T соответственно в области двухосного сжатия и растяжения по формулам:
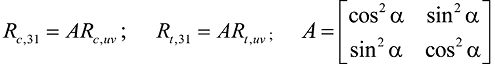 , (9)
, (9)
где А – матрица поворота.
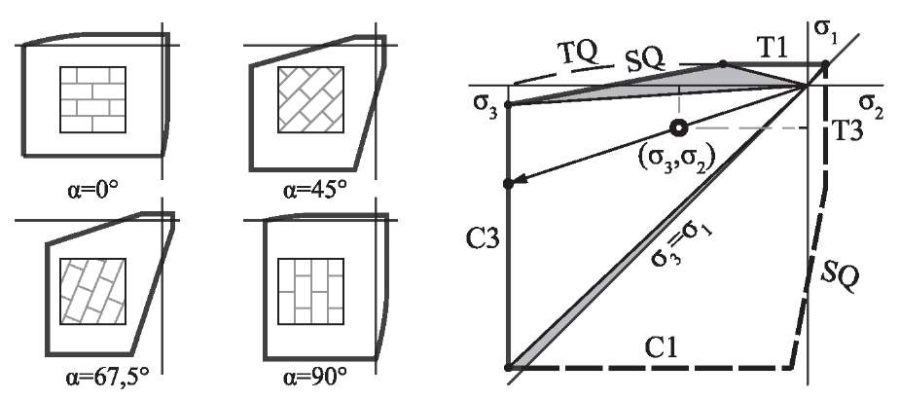
Рис. 3. Фигура прочности каменной кладки при плоском напряженном состоянии
Fig. 3. Strength figure of masonry in plane stress state
Предельная кривая прочности при действии главных растягивающих напряжений (TQ на рис. 3) может быть представлена в виде квадратичной параболы, огибающей предельные круги Мора при одноосном растяжении и сжатии. Уравнение такой параболы имеет вид:
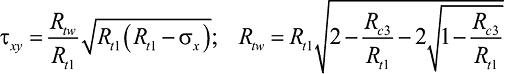 , (10)
, (10)
где σx – нормальное напряжение на площадке предельных касательных напряжений;
Rtw – расчетное сопротивление главным растягивающим напряжениям, которое в общем случае определяется экспериментально, а при условии огибания предельных кругов Мора может быть выражено через расчетные сопротивления при одноосном сжатии и растяжении.
Индексы в уравнении (10) указывают на то, что значение соответствующих расчетных сопротивлений, вычисляемых по формулам (9), берутся на взаимно перпендикулярных главных площадках.
Напряжения на главных площадках σ31 = (σ3, σ1, 0)T могут быть выражены через напряжения на площадках предельных касательных напряжений σxy = (σx, σy, τxy)T по формуле:
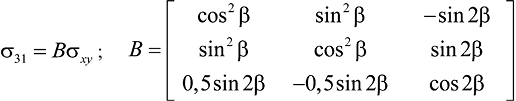 , (11)
, (11)
где В – матрица поворота;
β – угол между максимальным главным напряжением и нормальным напряжением на предельной площадке сдвига.
Таким образом, уравнение (10), соответствующее условию прочности при действии главных растягивающих напряжений, может быть представлено в главных напряжениях в виде функции f (σ3, σ1), заданной параметрически через σx:
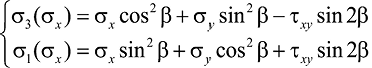 , (12)
, (12)
где
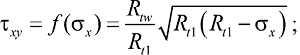
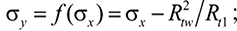
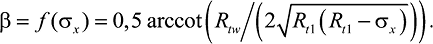
При увеличении угла α между горизонтальными швами кладки и площадками главных напряжений разрушение происходит за счет сдвига по неперевязанным швам. Данное предельное состояние (SQ на рис. 3) в осях ортотропии нормами представлено в виде уравнения τuv = Rsq – μσu. Согласно уравнению (11), оно может быть преобразовано к функции в координатах главных напряжений:
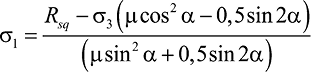 . (13)
. (13)
Уравнения (9), (12), (13) в координатах главных напряжений ограничивают область допускаемых напряжений и формируют объединенную фигуру прочности. На рис. 3 представлены конфигурации данной фигуры при разных углах α наклона главных осей к осям ортотропии.
Таким образом, зная фигуру прочности каменной кладки, можно описать поверхности предельных напряжений σu = f (ξ, α), τuv = f (ξ, α) (рис. 4).
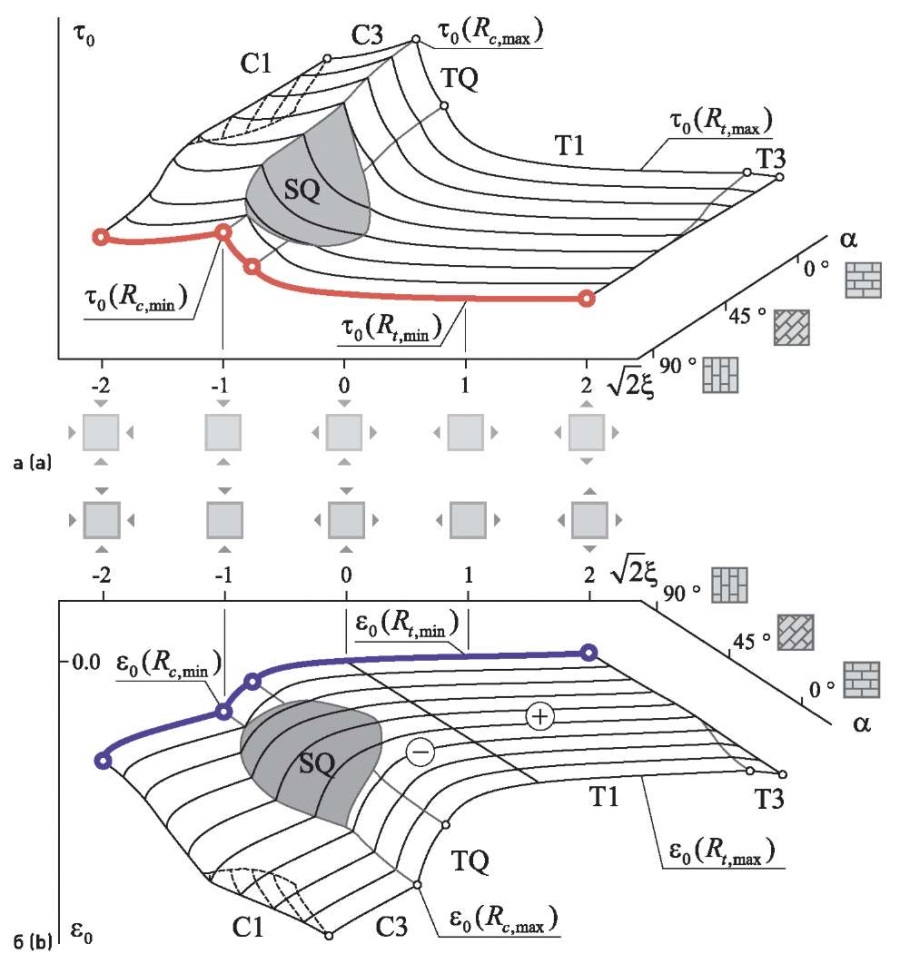
Рис. 4. Поверхности предельных касательных (а) и нормальных (б) октаэдрических напряжений
Fig. 4. Surfaces of limiting octahedral shear (a) and normal (b) stresses
Предельная поверхность в осях главных деформаций
Поскольку для анизотропного тела векторы октаэдрического касательного напряжения и октаэдрической сдвиговой деформации не коллинеарны в пространстве главных деформаций, то для задания функции γu = f (ω, χ, α) введем предельную поверхность по типу Сен-Венана (рис. 5а), ограничивающую три главных напряжения в зоне растяжения.
Тогда для каждого радиус-вектора может быть определено значение предельной сдвиговой деформации γu (рис. 5б) и в общем случае предельной средней деформации εu (рис. 5в) путем разложения полного вектора ε на его составляющие.
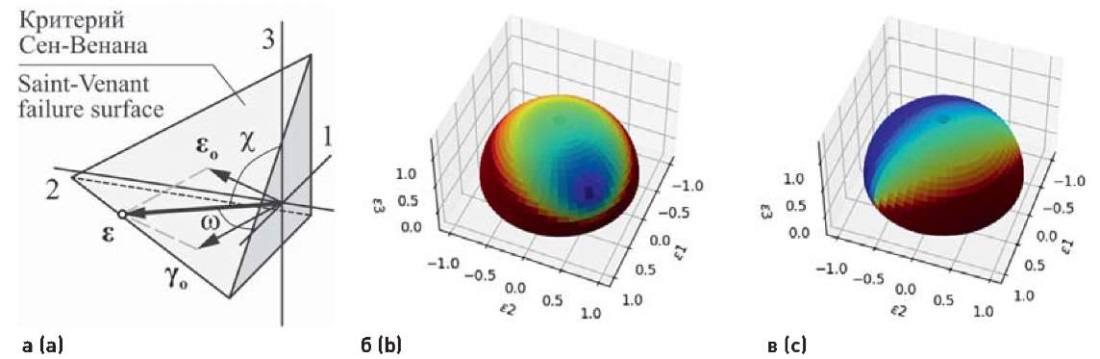
Рис. 5. Предельная поверхность в осях главных деформаций (а) и предельные значения деформаций на единичной сфере: б – сдвиговые γu; в – средние нормальные εu
Fig. 5. Limit surface in the axes of principal deformations (a) and limit values of deformations on a unit sphere: b – shear γu; с – average normal εu
Заключение
Описана деформационная теория каменных кладок как квазиортотропного материала с учетом ортотропии прочностных свойств и без учета деформационной анизотропии. Предложена фигура прочности каменных кладок при плоском напряженном состоянии, зависящая от угла между главными осями и осями ортотропии. Описана методика трансформации двух базовых кривых деформирования каменных кладок.
Полученные результаты позволяют производить расчет неармированных каменных кладок стен по деформационной теории путем трансформации кривых деформирования с учетом вида напряженного состояния и угла поворота главных осей относительно осей ортотропии.
Список литературы
1. СП 14.13330.2018. Строительство в сейсмических районах. Актуализированная редакция СНиП II-7-81* [интернет]. Режим доступа: https://www.minstroyrf.gov.ru/docs/17067/
2. EN 1998-1-1:2024. Eurocode 8. Design of structures for earthquake resistance – General rules and seismic action. https://doi.org/10.3403/30439956u
3. <i>Кабанцев О.В</i>. Пластическое деформирование и разрушение каменной кладки в условиях двухосного напряженного состояния. Вестник МГСУ. 2016;(2):34–48.
4. <i>Джинчвелашвили Г.А., Булушев С.В., Колесников А.В</i>. Нелинейный статический метод анализа сейсмостойкости зданий и сооружений. Сейсмостойкое строительство. Безопасность сооружений. 2016;(5):39–47.
5. <i>Кабанцев О.В</i>. Дискретная модель каменной кладки в условиях двухосного напряженного состояния. Вестник Томского государственного архитектурно-строительного университета. 2015;(4):113–134.
6. <i>Lourenco P.B., De Borst R., Rots J.G</i>. A plane stress softening plasticity model for orthotropic materials. International Journal for Numerical Methods in Engineering. 1997;40(21):4033–4057. https://doi.org/10.1002/
7. (sici)1097-0207(19971115)40:21<4033::aid-nme248>3.0.co;2-0
8. <i>Lourenco P</i>. Anisotropic Softening Model for Masonry Plates and Shells. Journal of structural engineering. 2000;126(9):1008–1016. https://doi.org/10.1061/(asce)0733-9445(2000)126:9(1008)
9. <i>Поздеев М.Л., Лихачева С.Ю., Смагин И.В., Радайкин О.В</i>. Расчет каменных стен с использованием деформационной теории пластичности. Вестник Казанского государственного энергетического университета. 2023;15(3):163–174.
10. <i>Фиалко С.Ю</i>. Четырехузловой конечный элемент для моделирования поведения тонкостенных железобетонных конструкций. Инженерно-строительный журнал. 2014;(5):27–36.
11. <i>Тюпин Г.А</i>. Деформационная теория пластичности каменной кладки. Строительная механика и расчет сооружений. 1980;(6):28–30.
12. <i>Гениев Г.А</i>. Вариант деформационной теории пластичности бетона. Бетон и железобетон. 1969;(2):18.
13. <i>Круглов В.М., Ерофеев В.Т., Ватин Н.И., Аль Дулайми Салман Давуд Салман</i>. Вариант деформационной теории пластичности бетона в плоском напряженном состоянии. Транспортные сооружения [интернет]. 2019;(4). Режим доступа: https://t-s.today/PDF/11SATS419.pdf.
14. <i>Деркач В.Н</i>. Анизотропия деформационных свойств каменной кладки. Глобальная энергия. 2011;(1):201–207.
15. <i>Alwathaf A., Thanoon W., Jaafar M., Noorzaei J</i>. Mathematical modelling of stress-strain curves of masonry materials. Australian Journal of Structural Engineering. 2013;13:219–230. https://doi.org/10.7158/s11-110.2012.13.3
16. <i>Поздеев М.Л., Лихачева С.Ю</i>. Подбор параметров аппроксимирующей кривой диаграммы сжатия каменной кладки. Приволжский научный журнал. 2023;(3):34–41.
17. <i>Kaushik H., Rai D., Jain S., Asce M</i>. Stress-strain characteristics of clay brick masonry under uniaxial compression. Journal of Materials in Civil Engineering. 2007;19(9): 728–739. https://doi.org/10.1061/
18. (asce)0899-1561(2007)19:9(728)
19. <i>Doerr A., Gebbeken N., Larcher M., Steyerer M</i>. The effect of near-field explosions on masonry walls [internet]. In: ISIEMS/ICPSAt: Potsdam, Germany; 2013. https://www.researchgate.net/publication/298788966_
20. The_Effect_of_Near-Field_Explosions_on_Masonry_Walls
21. <i>Page A.W</i>. The biaxial compressive strength of brick masonry. Proceedings of the Institution of Civil Engineers. 1981;71(3):893–906. https://doi.org/10.1680/iicep.1981.1825
22. <i>Page A.W</i>. The strength of brick masonry under biaxial tension-compression. International journal of masonry construction. 1983;3(1):26–31.
23. <i>Поздеев М.Л., Смагин И.В</i>. Сравнение критериев прочности неармированной каменной кладки в области двуосного сжатия. В: XI Всероссийский Фестиваль науки: сб. докладов, Нижний Новгород, 20–21 октября 2021 г. Нижний Новгород: Нижегородский государственный архитектурно-строительный университет; 2021, с. 200–204.
24. <i>Гениев Г.А., Курбатов А.С., Самедов Ф.А</i>. Вопросы прочности и пластичности анизотропных материалов. Москва: Интербук; 1993.
Об авторах
М. Л. ПоздеевРоссия
Максим Леонидович Поздеев*, аспирант кафедры теории сооружений и технической механики, ННГАСУ, Нижний Новгород; инженер-исследователь, ООО «Автоматизация проектных работ» (ГК «SCAD Soft»), Москва
ул. Ильинская, д. 65, г. Нижний Новгород, 603000, Российская Федерация; Рубцовская наб., д. 4, к. 1, помещ. VII, г. Москва, 105082, Российская Федерация
e-mail: maksim.leon.pz@yandex.ru
С. Ю. Лихачева
Россия
Светлана Юрьевна Лихачева, канд. физ.-мат. наук, доцент, профессор кафедры теории сооружений и технической механики, ННГАСУ, Нижний Новгород
ул. Ильинская, д. 65, г. Нижний Новгород, 603000, Российская Федерация
e-mail: lihsvetlana@yandex.ru
И. В. Смагин
Россия
Илья Васильевич Смагин, аспирант кафедры теории сооружений и технической механики, ННГАСУ, Нижний Новгород
ул. Ильинская, д. 65, г. Нижний Новгород, 603000, Российская Федерация
e-mail: ivsmag@vk.com
Рецензия
Для цитирования:
Поздеев М.Л., Лихачева С.Ю., Смагин И.В. Квазиортотропная деформационная теория пластичности каменных кладок при плоском напряженном состоянии. Вестник НИЦ «Строительство». 2024;43(4):218-231. https://doi.org/10.37538/2224-9494-2024-4(43)-218-231. EDN: CYKUXR
For citation:
Pozdeev M.L., Likhacheva S.Yu., Smagin I.V. Quasi-orthotropic deformation theory of masonry plasticity in plane stress state. Bulletin of Science and Research Center of Construction. 2024;43(4):218-231. (In Russ.) https://doi.org/10.37538/2224-9494-2024-4(43)-218-231. EDN: CYKUXR
JATS XML


























