Перейти к:
Напряженно-деформированное состояние каменных крестовых сводов
https://doi.org/10.37538/2224-9494-2024-4(43)-182-194
EDN: DRQFSH
Аннотация
Введение. Вплоть до настоящего времени расчет каменных сводов исторических зданий предусматривает подход, в котором своды рассматриваются как элементы, «собранные» из трех-, двух- и бесшарнирных арок, определение усилий в которых выполняется по общим правилам строительной механики. Однако возможности подобного подхода к анализу пространственно работающих конструкций (крестовые своды), выполненных из материала, отличающегося прочностной анизотропией (каменная кладка), крайне ограничены.
Цель. Установление закономерностей формирования параметров напряженно-деформированного состояния каменного крестового свода при восприятии им равномерно-распределенной нагрузки, а также влияния прочностной анизотропии каменной кладки на прочность свода.
Материалы и методы. Анализ напряженно-деформированного состояния каменного крестового свода выполнен в расчетном комплексе конечно-элементного моделирования высокого уровня в твердотельной пространственной гомогенной постановке. Выполнен анализ влияния прочностной анизотропии каменной кладки и неодноосности напряженного состояния в отдельных областях свода на его прочность.
Результаты. Установлено, что наиболее неблагоприятное напряженное состояние складывается в центральной области крестового свода снизу по осям распалубок, где формируется двухосное растяжение равной интенсивности, сопротивление которому характеризуется как крайне низкое. Установлено, что напряженно-деформированное состояние находится в зависимости от отношения стрелы подъема f к пролету свода L (f/L). Выявлено, что прочность каменного крестового свода зависит в том числе от ориентации усилий относительно растворных швов кладки; значимым оказывается неодноосность действия усилий в отдельных областях.
Выводы. Наибольшее значение на формирование напряженно-деформированного состояния каменного крестового свода, кроме его пролета и толщины, оказывает отношение стрелы подъема f к пролету свода L (f/L). Прочностной анализ крестовых сводов следует вести с учетом ориентации усилий относительно растворных швов кладки с учетом неодноосности действия усилий в отдельных областях.
Ключевые слова
Для цитирования:
Зимин С.С. Напряженно-деформированное состояние каменных крестовых сводов. Вестник НИЦ «Строительство». 2024;43(4):182-194. https://doi.org/10.37538/2224-9494-2024-4(43)-182-194. EDN: DRQFSH
For citation:
Zimin S.S. Stress-strain state of stone cross vaults. Bulletin of Science and Research Center of Construction. 2024;43(4):182-194. (In Russ.) https://doi.org/10.37538/2224-9494-2024-4(43)-182-194. EDN: DRQFSH
Введение
В исторических зданиях, построенных до 1917 г., широкое применение нашли перекрытия в виде крестовых сводов (рис. 1). Характерной особенностью крестовых сводов является передача давления посредством ребер в четыре угловые «точки» (на колонны), что обусловило применение данных сводов для перекрытия помещений (пространств), к которым предъявлялись требования хорошей освещенности и «свободной планировки» (рис. 1а). Также крестовыми сводами перекрывались помещения, ограниченные стенами (рис. 1б).

Черными стрелками показана схема передачи усилий в своде через ребра на опоры
Рис. 1. Система крестовых сводов, устроенных по колоннам (а), и крестовый свод, ограниченный несущими стенами (б)
Black arrows show the direction of force transmission in the vault through the ribs to the supports
Fig. 1. System of cross vaults supported by columns (a), and a cross vault bounded by load-bearing walls (b)
Геометрически крестовые своды образованы пересечением двух цилиндрических сводов с последующим «сохранением» верхних частей – распалубок (рис. 2а). При этом каждую из распалубок возможно рассматривать как составленную из условных арок (рис. 2б), передающих усилия на ребра, которые передают их на опоры посредством опорных консолей (выносных пят). Следует отметить, что ребра крестовых сводов (при отсутствии их утолщения в виде гурт и пр.) не являются отдельными конструктивными элементами и обусловлены «геометрией» формирования примыкающих друг к другу распалубок. Кладка опорных консолей крестовых сводов перевязывалась с кладкой опорных конструкций, а щеки сводов не имели опирания на стены (распалубки вплотную примыкали к стенам).
Крестовые своды устраивались как пологими – с отношением стрелы подъема к пролету f/L = 0,1, так и полуциркульными – с отношением f/L = 0,5, а также с промежуточными значениями данного отношения (рис. 2в). Поверх крестовых сводов устраивалась засыпка, сверху – деревянный пол.
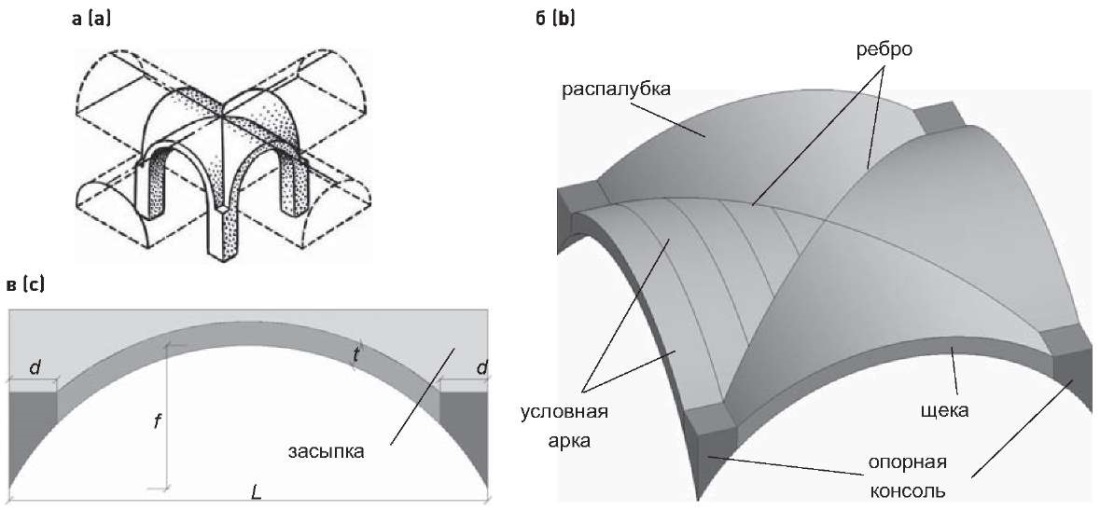
L – пролет; f – стрела подъема; t – толщина; d – ширина опорных консолей
Рис. 2. Конструктивные особенности крестового свода: а – формирование крестового свода из двух цилиндрических сводов; б, в – модель крестового свода и его основные части и параметры
L – span; f – rise; t – thickness; d – width of support consoles
Fig. 2. Structural features of a cross vault: a – formation of a cross vault from two cylindrical vaults; b, c – model of a cross vault and its main parts and parameters
Конструктивно-технологические аспекты устройства сводов описаны в работах [1–5] XIX – начала XX века. Расчет того времени предусматривал подход, в котором своды рассматриваются как элементы, «собранные» из отдельных клиньев с последующим построением и анализом кривой давления [6][7]. При этом уже в то время каменные своды не рассматривались для потенциального применения в новых зданиях, что было обусловлено переориентацией конструктивных решений перекрытий на плоские по стальным балкам и железобетонные. В итоге на протяжении всего советского периода каменные своды воспринимались как конструкции в составе объектов реставрации и реконструкции, а расчет предусматривал подход, в котором они рассматриваются как элементы, «собранные» из трех-, двух- и бесшарнирных арок, определение усилий в которых выполняется по общим правилам строительной механики [8][9]. Современные конечно-элементные расчетные комплексы дают возможность для более детального анализа работы сводов.
Ниже представлены результаты анализа напряженного-деформированного состояния крестового свода пролетом L = 5 м, толщиной t = 0,25 м, шириной опорных консолей d = 0,5 м, с первоначальным отношением стрелы подъема к пролету f/L = 0,3 и последующим варьированием данного отношения f/L = (0,1÷0,5). Численный анализ выполнен в комплексе конечно-элементного моделирования высокого уровня в твердотельной постановке. Граничные условия задавались с учетом описанных выше конструктивных особенностей устройства опорных консолей, для которых задано жесткое сопряжение на опорах, и щековых участков, для которых ограничивались лишь горизонтальные перемещения в направлении «от сводов». Плотность кладки свода принята равной 2000 кг/м 3, плотность засыпки – 1000 кг/м 3 (засыпка принята устроенной выше шелыги на половину толщины свода). Сверху задана обобщенная равномерно-распределенная нагрузка 5 кПа (стяжка, пол, полезная нагрузка, временные перегородки).
Числовые значения границ цветовых шкал изополей и числовые значения оси ординат графиков соответствуют значениям расчетных сопротивлений кладки сжатию и растяжению при изгибе в соответствии с СП 15.13330.2020 [10], что дает возможность использовать результаты нижеприведенных численных исследований для кладок с различными марками кирпича и раствора.
Анализ напряженно-деформированного состояния крестового свода
Деформированное (и, соответственно, напряженное) состояние крестового свода обусловлено работой условных арок распалубок «по арочной схеме» с передачей усилий на ребра (рис. 3). Горизонтальные составляющие равнодействующих усилий (распор) в арках при их сопряжении с условными ребрами уравновешиваются распором арок примыкающих распалубок. Вертикальные составляющие усилий передаются на условные ребра, которые передают их на опорные консоли также «по арочной схеме». При этом ребра испытывают существенно большие деформации по сравнению с арками (u > u`). По сути, именно деформирование ребер (их жесткость) определяет общее деформирование крестового свода «по плитной схеме» с «провисанием» центральной области.
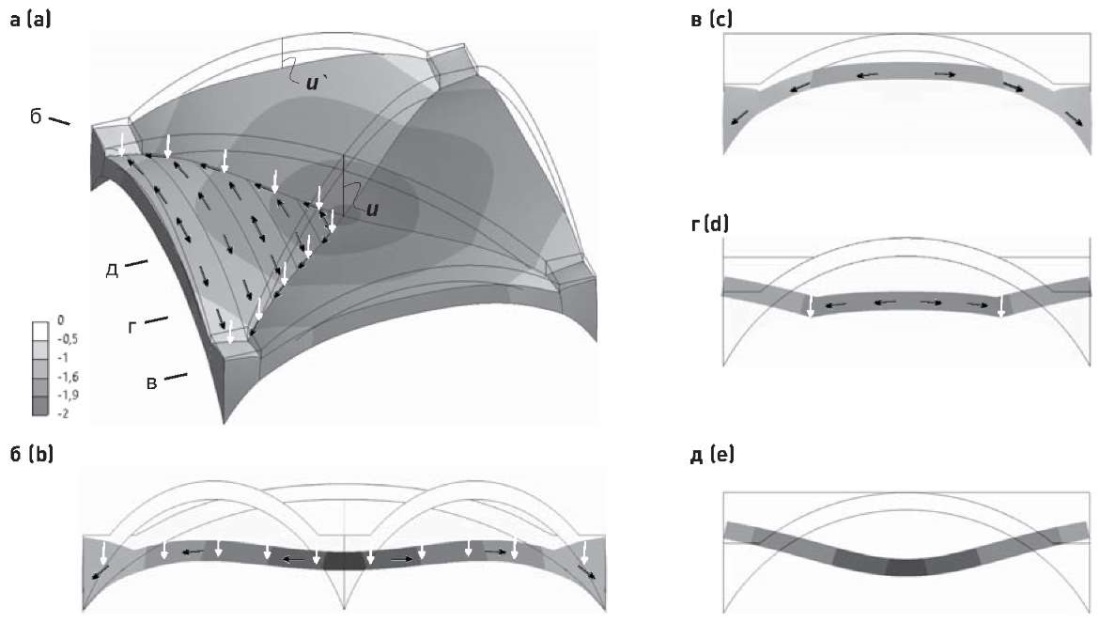
Крестовый свод: L = 5 м; f/L = 0,3; t = 0,25 м; d = 0,5 м
Черными стрелками показана схема передачи усилий в условных арках на ребра и далее на опоры, белыми стрелками – вертикальные составляющие равнодействующих усилий при сопряжении арок с ребрами
Рис. 3. Деформированное состояние крестового свода (коэффициент масштабирования k = 500)
Cross vault: L = 5 m; f/L = 0.3; t = 0.25 m; d = 0.5 m
Black arrows indicate force transmission in conditional arches to ribs and further to supports; white arrows indicate vertical components of resultant forces at the junction between arches and ribs
Fig. 3. Deformed state of the cross vault (scaling factor k = 500)
Растягивающие напряжения наибольшей интенсивности действуют (рис. 4):
– снизу свода в его центральной области при сопряжении распалубок с ребрами на некотором расстоянии от центра (точки 1). Напряжения σ1 ориентированы поперек ребер, при этом напряжения, ориентированные вдоль ребер, стремятся к нулю (одноосное растяжение). Непосредственно в центре свода (точка 2) интенсивность напряжений σ1 меньше, однако в ортогональном направлении действуют растягивающие напряжения σ2, значения которых равны значениям напряжений σ1 (двухосное растяжение равной интенсивности). При этом в центральной области свода по осям распалубок (линии 2–3) действуют напряжения σ1 и σ2, значения которых соизмеримы и ориентированные вдоль и поперек осей распалубок (двухосное растяжение равной интенсивности);
– снизу свода по его периметру посередине распалубок (точки 3 на осях распалубок у щек), где их интенсивность в среднем в два раза меньше интенсивности напряжений в центре свода. Напряжения σ1 ориентированы вдоль условных арок распалубок свода, при этом напряжения в ортогональном направлении стремятся к нулю (одноосное растяжение);
– сверху свода по его периметру в крайних третях распалубок (точки 4, при уменьшении отношения f/L данные области перемещаются к опорным консолям). Интенсивность напряжений σ1 существенно меньше, чем в центральной области (в среднем в 3 раза), при этом в ортогональном направлении (вдоль условных арок распалубок) действуют сжимающие напряжения σ3 (рис. 5), интенсивность которых на порядок больше интенсивности напряжений σ1. Эти обстоятельства позволяют не рассматривать данные области при анализе образования первичных трещин в своде.
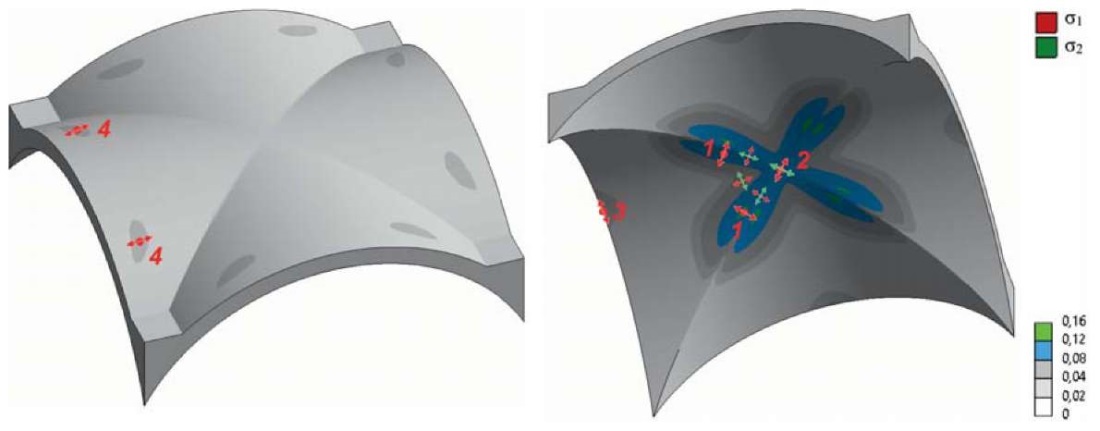
Крестовый свод: L = 5 м; f/L = 0,3; t = 0,25 м; d = 0,5 м
Точки 1–4, где действуют напряжения наибольшей интенсивности, замаркированы на одной распалубке, на трех других распалубках точки расположены симметрично
Рис. 4. Главные растягивающие напряжения σ1 и σ2 на поверхностях крестового свода (МПа) и их траектория
Cross vault: L = 5 м; f/L = 0.3; t = 0.25 m; d = 0.5 m
Points 1–4, where the highest intensity stresses act, are marked on one groin; on three other groins, points are located symmetrically
Fig. 4. Principal tensile stresses σ1 and σ2 on the surfaces of the cross vault (MPa) and their trajectory
Сжимающие напряжения наибольшей интенсивности действуют (рис. 5):
– снизу свода у опор вдоль его ребер (точки 5 и опорные консоли в целом). Напряжения σ3 в опорных консолях ориентированы к опорной точке, при этом в ортогональном направлении напряжения стремятся к нулю (одноосное сжатие). Следует отметить, что интенсивность напряжений σ3 в опорных консолях в среднем в два раза больше, чем в центральной области;
– сверху свода в центральной области вдоль ребер на некотором расстоянии от центра (точки 6). Напряжения σ3 ориентированы поперек ребер свода (к опорам напряжения σ3 ориентированы вдоль ребер). Вдоль ребер действуют сжимающие напряжения σ2, интенсивность которых близка к интенсивности напряжений σ3. Непосредственно в центре свода (точка 7) интенсивность напряжений σ3 меньше, однако значения σ3 и σ2 равны друг другу. При этом во всей центральной области свода действуют напряжения σ3 и σ2, значения которых соизмеримы и ориентированные вдоль и поперек осей распалубок (двухосное сжатие равной интенсивности).
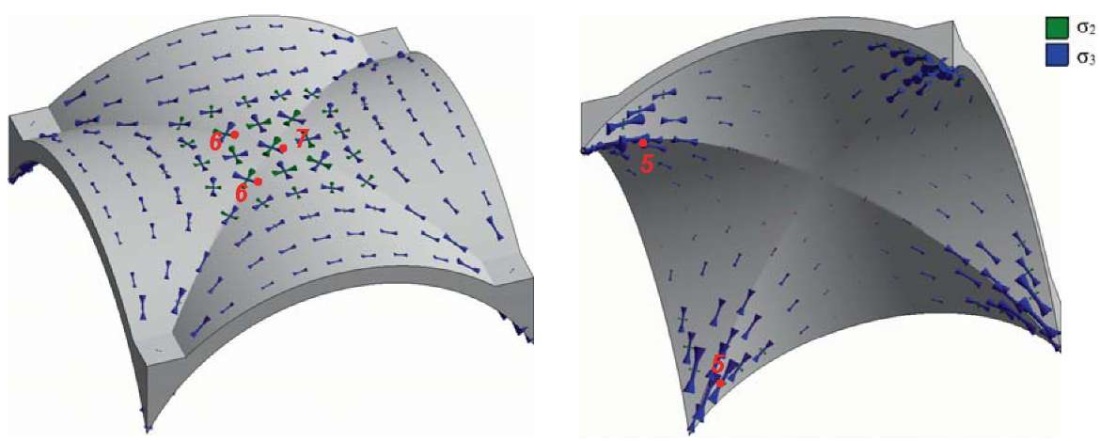
Крестовый свод: L = 5 м; f/L = 0,3; t = 0,25 м; d = 0,5 м
Точки 5–7, где действуют напряжения наибольшей интенсивности, замаркированы на одной распалубке, на трех других распалубках точки расположены симметрично
Рис. 5. Траектория главных сжимающих напряжений σ2 и σ3 на поверхностях крестового свода
Cross vault: L = 5 м; f/L = 0.3; t = 0.25 m; d = 0.5 m
Points 5–7, where the highest intensity stresses act, are marked on one groin; on three other groins, points are located symmetrically
Fig. 5. Trajectory of principal compressive stresses σ2 and σ3 on the surfaces of the cross vault
Интенсивность как растягивающих, так и сжимающих напряжений во всех анализируемых точках увеличивается при уменьшении отношения f/L от 0,5 до 0,1 (рис. 6). При f/L < 0,3 наблюдается резкое увеличение напряжений, что наиболее существенно проявляется при f/L < 0,2. Так, растягивающие напряжения σ1 в точке 1 при уменьшении f/L от 0,5 до 0,3 увеличиваются на 15 %, при уменьшении f/L от 0,3 до 0,2 увеличение составляет 35 %, от 0,2 до 0,1 – 115 %.
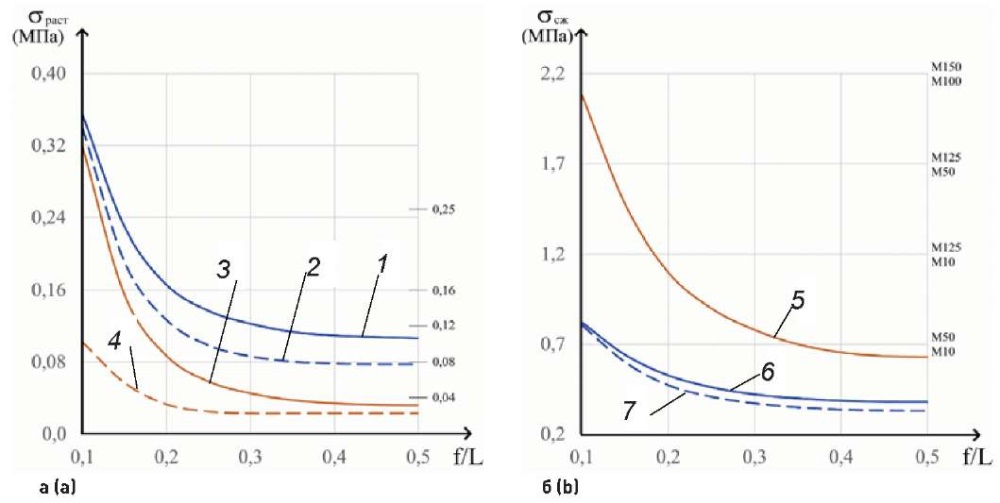
Крестовый свод: L = 5 м; t = 0,25 м; d = 0,5 м
1–4 – номера точек в соответствии с рис. 4; 5–7 – номера точек в соответствии с рис. 5
Рис. 6. Изменение главных растягивающих (а) и сжимающих (б) напряжений в наиболее напряженных областях (точках 1–7) в зависимости от отношения f/L
Cross vault: L = 5 м; t = 0.25 m; d = 0.5 m
1–4 – point numbers corresponding to Fig. 4; 5–7 – point numbers corresponding to Fig. 5
Fig. 6. Variation of principal tensile (a) and compressive (b) stresses in the most stressed areas (points 1–7) as a function of the ratio f/L
Аналогичным закономерностям подчиняются вертикальные перемещения свода и распор в опорных консолях (рис. 7). При уменьшении f/L от 0,5 до 0,1 величина распора H увеличивается более чем в 2 раза, вертикальные перемещения центра свода – более чем в 4 раза. Уменьшение вертикальной составляющей опорной реакции V при уменьшении f/L от 0,5 до 0,1 объясняется уменьшением объема как кладки свода, так и устроенной по нему засыпки.
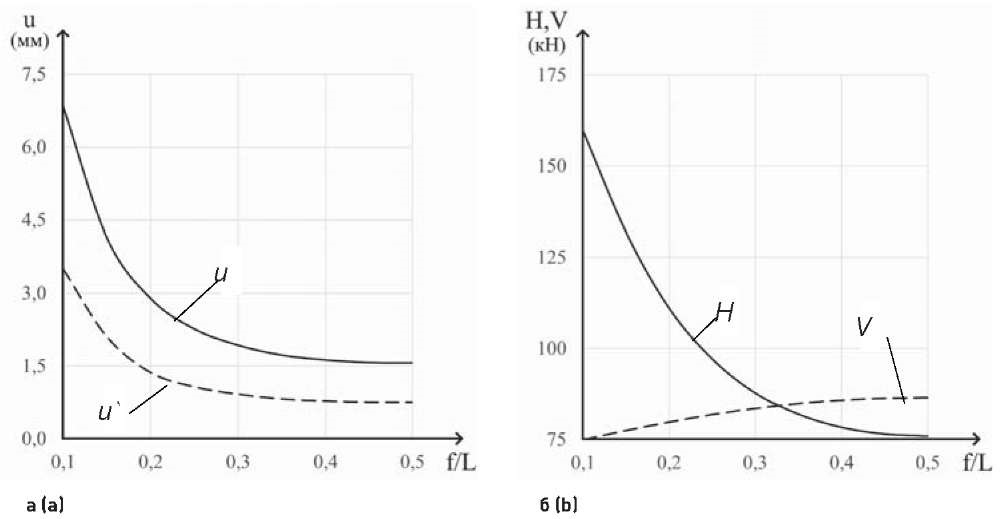
Крестовый свод: L = 5 м; t = 0,25 м; d = 0,5 м
u, u` – вертикальные перемещения соответственно центра свода и условных арок при сопряжении со стенами (рис. 3); H, V – соответственно горизонтальная (распор) и вертикальная составляющие опорной реакции в одной опоре (опорной консоли)
Рис. 7. Изменение вертикальных перемещений u центра свода (а) и опорных реакций H и V в одной опорной консоли (б) в зависимости от отношения f/L
Cross vault: L = 5 m; t = 0.25 m; d = 0.5 m
u, u` – vertical displacements of the vault center and the conditional arches at the junction with the walls, respectively (Fig. 3); H, V – horizontal (thrust) and vertical components of the support reaction in one support (support console), respectively
Fig. 7. Variation of vertical displacements u of the vault center (a) and support reactions H and V in one support console (b) as a function of the ratio f/L
Прочностной анализ крестового свода
Существенной при проведении прочностного анализа крестового свода оказывается система устройства кладки (перевязка кладки распалубок). Кладка распалубок производилась со швами (горизонтальными швами кладки), нормальными или к щековым поверхностям (рис. 8а), или к диагональным ребрам (рис. 8б). При этом первый вариант встречается при обследовании исторических зданий существенно чаще.

Напряженное состояние «в укрупненном виде» показано на одной распалубке, на трех других распалубках напряженное состояние симметрично
Рис. 8. Устройство кладки распалубок крестового свода: а – со швами нормальными к щековым поверхностям (вариант 1); б – со швами нормальными к диагональным ребрам или «в елку» (вариант 2)
The stress state is illustrated in a detailed view on one groin, while on three other groins, the stress state is symmetrical
Fig. 8. Arrangement of masonry of cross vault groins: a – with joints to the spandrel (variant 1); b – with joints to the diagonal ribs, herringbone pattern (variant 2)
Выше обосновано, что как растягивающие, так и сжимающие напряжения наибольшей интенсивности действуют снизу свода, в связи с чем на рис. 8 на одной из распалубок показано напряженное состояние свода «в укрупненном виде». Из рисунка видно, что как сжимающие, так и растягивающие напряжения действуют под разными углами относительно горизонтальных растворных швов (далее – опорных швов) в зависимости от местоположения анализируемой точки и системы перевязки кладки.
Характерной особенностью кирпичной кладки является анизотропия ее прочности, при которой сопротивление как сжатию, так и растяжению зависит от ориентации данных усилий относительно опорных швов [11] (рис. 9а, б). Анализ прочности кладки при двухосном напряженном состоянии возможно вести, основываясь на эмпирических критериях прочности. В российской практике наиболее известным является эмпирический критерий прочности Г. А. Гениева [12] (рис. 9в), за рубежом – критерий, предложенный A. W. Page [13] (рис. 9г).
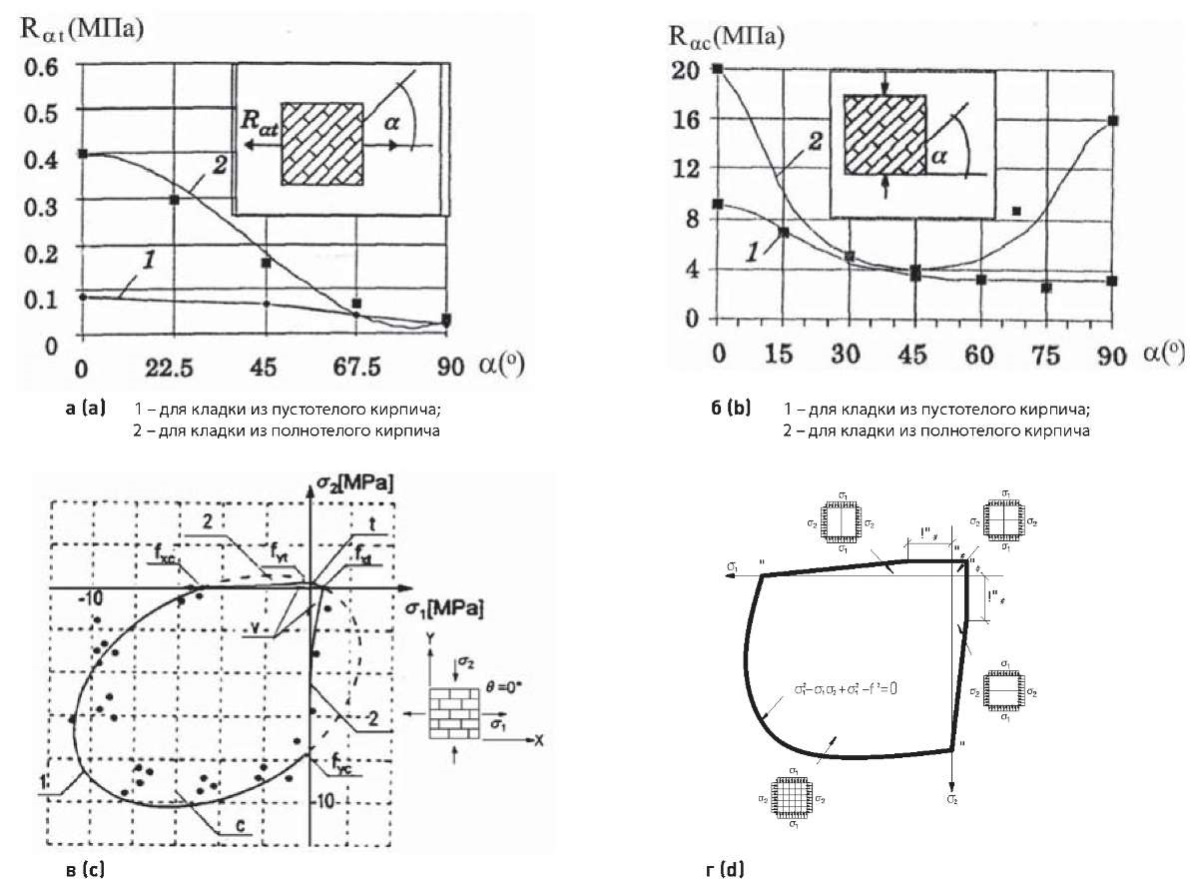
Рис. 9. К прочностному анализу кирпичной кладки: а, б – сопротивление кладки соответственно сжатию и растяжению под различными углами к растворным швам согласно [11]; в, г – критерий прочности кладки соответственно согласно [12][13]
Fig. 9. Strength analysis of brick masonry: a, b – resistance of masonry to compression and tension at various angles to the mortar joints according to [11]; c, d – masonry strength criterion according to [12][13]
Показано, что в центральной области снизу свода по осям распалубок складывается двухосное растяжение равной интенсивности. При первом варианте перевязки кладки (рис. 8а) растягивающие напряжения действуют под углом 0° и 90° к опорным швам (растяжение по перевязанным и неперевязанным сечениям), при втором варианте (рис. 8б) – под углом 45° к опорным швам. При любом из обозначенных вариантов перевязки сопротивление кладки двухосному растяжению характеризуется как крайне низкое (рис. 9в, г). По периметру свода посередине распалубок (на осях распалубок у щек) растягивающие напряжения σ1 действуют (рис. 8): при первом варианте перевязки кладки – под углом 90° к опорным швам (растяжение по неперевязанным сечениям), при втором варианте – под углом 45° к опорным швам (растяжение по условно перевязанным сечениям). При этом интенсивность напряжений в среднем в два раза меньше интенсивности напряжений в центре свода.
При обследовании крестовых сводов наиболее часто фиксируются трещины, развивающиеся именно вдоль осей распалубок (рис. 10) и в первую очередь в центральной области свода (при этом возможно провисание центральной области), с последующим развитием трещин вдоль осей к щекам. Данная картина поврежденности наиболее выражена для пологих сводов, что обосновывается результатами выполненных численных исследований (рис. 6, 7). При этом инициирующим фактором появления трещин может явиться, например, подвижка опор свода из-за неравномерных осадок фундаментов, податливости опор распору и пр. (распор в опорных консолях также возрастает при уменьшении отношения f/L).
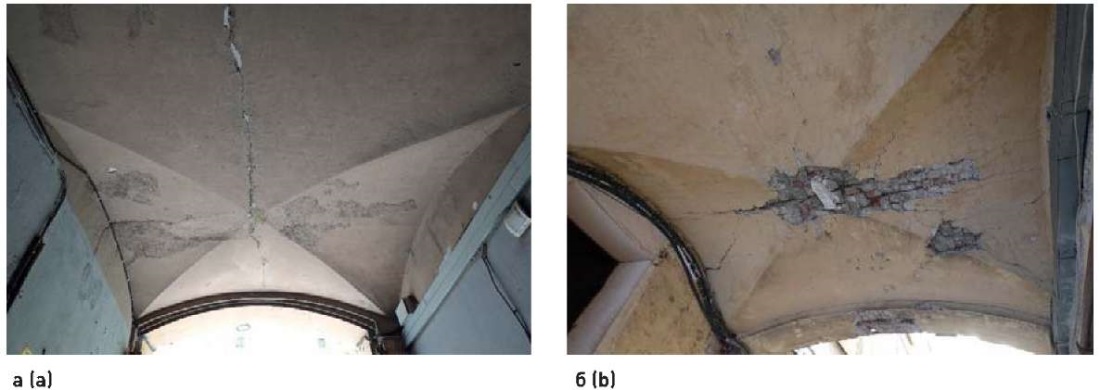
Рис. 10. Трещинообразование в крестовом своде
Fig. 10. Cracking in the cross vault
При сопряжении распалубок с ребрами свода значения растягивающих напряжений больше, чем во всей центральной области, однако в данных зонах формируется одноосное растяжение, при котором напряжения σ1 действуют: при первом варианте перевязки кладки – под углом 45° к опорным швам (растяжение по условно перевязанным сечениям), при втором варианте перевязки – 0° к опорным швам, то есть вдоль опорных швов (растяжение по перевязанным сечениям). Сопротивление кладки растяжению по перевязанным швам выше сопротивления двухосному растяжению. В итоге трещины при сопряжении распалубок с ребрами образуются «во вторую очередь», то есть после существенного развития вышеописанных повреждений (рис. 10б). Также трещины в данных зонах образуются при неравномерных подвижках опор свода.
В опорных консолях сжимающие напряжения действуют: при первом варианте перевязки кладки (рис. 8а) – под углом 45° к опорным швам, когда сопротивление кладки сжатию минимально (рис. 9б), при втором варианте (рис. 8б) – под углом 90° к опорным швам.
Из рис. 6б видно (кривая 5), что при отношении f/L > 0,3 сжимающие напряжения близки к расчетному сопротивлению кладки сжатию R = 0,7 МПа в соответствии с СП 15.13330.2020 [10] для кирпича марки М50 и раствора марки М10, при f/L = 0,2 – к значению R = 1,2 МПа для кирпича марки М125 и раствора марки М10, а при f/L = 0,1 – к значению R = 2,2 МПа для кирпича марки М150 и раствора марки М100. При этом регламентированные СП 15.13330.2020 [10] расчетные сопротивления R установлены из испытаний, когда сжимающие усилия действуют под углом 90° к опорным швам (R = R90). Для крестовых сводов при первом варианте перевязки кладки, когда сопротивление кладки сжатию R45 существенно (до пяти раз) меньше приведенных выше значений R90 = R, напряжения в опорных консолях становятся критическими, а для пологих сводов могут на порядок превышать значения R45.
Однако при обследовании каменных крестовых сводов ситуации силового раздробления кладки опорных консолей встречаются редко (в основном фиксируются трещины в распалубках). Объясняется это тем, что сжимающие напряжения указанной интенсивности действуют в локальной области, средние напряжения в опорных консолях существенно меньше. Кроме этого, расчетные сопротивления кладки сжатию R установлены [14] исходя из механизмов разрушения вертикальных образцов (стены, колонны) на центральное сжатие – механизм потери устойчивости «столбиков», на которые разделили кладку трещины. В итоге предельные напряжения в опорных консолях должны регламентироваться сопротивлением кладочных элементов местному сжатию (раздробление кладки консолей), что требует проведения дополнительных исследований.
Далее следует отметить, что верхняя центральная область свода испытывает двухосное сжатие равной интенсивности (рис. 5), при котором кладка характеризуется наибольшим сопротивлением (рис. 9в, г).
Заключение
Существенное влияние на формирование напряженно-деформированного состояния крестового свода оказывает отношение стрелы подъема к пролету f/L. Как растягивающие, так и сжимающие напряжения в областях с наибольшей их интенсивностью возрастают при уменьшении отношения f/L. При f/L < 0,3 наблюдается резкое увеличение напряжений, что наиболее существенно проявляется при f/L < 0,2. Аналогичным закономерностям подчиняются вертикальные перемещения свода (центральной области) и величина распора в опорах.
Наиболее неблагоприятное напряженное состояние складывается в центральной области крестового свода снизу по осям распалубок, где формируется двухосное растяжение равной интенсивности, сопротивление которому характеризуется как крайне низкое. Данное обстоятельство обосновывает образование фиксируемых при обследовании трещин вдоль распалубок, которые получают свое развитие из центра свода. При этом именно в пологих сводах фиксируется наибольшая степень поврежденности.
Существенное значение для прочности крестового свода имеет система устройства кладки (перевязка кладки распалубок). Так, сжимающие усилия в опорных консолях могут действовать (в зависимости от системы перевязки) как под углом 90°, так и под углом 45° к горизонтальным растворным швам. Сопротивление кладки при данных значениях угла может отличаться до пяти раз. Аналогично для растягивающих усилий, когда сопротивления растяжению по перевязанным и неперевязанным сечениям характеризуются различными значениями.
Отмеченные обстоятельства необходимо учитывать при обосновании картины поврежденности крестовых сводов исторических зданий и при проведении их поверочных расчетов.
Список литературы
1. <i>Красовский А.К</i>. Гражданская архитектура. Части зданий. 2-е изд. Москва; 1886.
2. <i>Романович М.Е</i>. Гражданская архитектура. Части зданий. Т. 2. Арки и своды. Санкт-Петербург; 1903.
3. <i>Кирштейн Г.В</i>. Строительное искусство: Руководство к возведению фабричных, гражданских и сельских строений. 3-е изд. Рига: Издание Н. Киммеля; 1909.
4. <i>Полищук А.А</i>. Курс строительного искусствам в связи с расчетами устойчивости и прочности частей сооружений. Ч. 4. Каменные стены и своды. Санкт-Петербург: Паровая скоропечатня П.О. Яблонского; 1913.
5. <i>Бернгард В.Р</i>. Арки и своды. Руководство к устройству и расчету арочных и сводчатых перекрытий. Ч. 1. Устройство арок и сводов. Санкт-Петербург: Типографiя Ю.Н. Эрлихъ; 1901.
6. <i>Лахтин Н.К</i>. Расчет арок и сводов. Москва: Студенческое Издательское Общество; 1911.
7. <i>Кривошеин Г.Г</i>. Расчет сводов. Петроград: Тип. Бенке; 1918.
8. <i>Бессонов Г.Б</i>. Исследование деформаций, расчет несущей способности и конструктивное укрепление древних распорных систем. Москва: Росреставрация; 1989.
9. <i>Пашкин Е.М., Бессонов Г.Б</i>. Диагностика деформации памятников архитектуры. Москва: Стройиздат; 1984.
10. СП 15.13330.2020. Каменные и армокаменные конструкции. Актуализированная редакция СНиП II-22-81 [интернет]. Режим доступа: https://www.minstroyrf.gov.ru/docs/117291/
11. <i>Орлович Р.Б., Найчук А.Я., Деркач В.Н</i>. Анизотропия прочности каменной кладки из кладочных элементов с щелевыми вертикальными пустотами. Строительная механика и расчет сооружений. 2010;(3):35–38.
12. <i>Гениев Г.А</i>. О критерии прочности каменной кладки при плоском напряженном состоянии. Строительная механика и расчет сооружений. 1979;(2):7–11.
13. <i>Page A.W</i>. The strength of brick masonry under biaxial compression-tension. International Journal of Masonry Construction. 1983;3(1):26–31.
14. <i>Онищик Л.И</i>. Каменные конструкции промышленных и гражданских зданий. Москва: Госстройиздат; 1939.
Об авторе
С. С. ЗиминРоссия
Сергей Сергеевич Зимин, канд. техн. наук, доцент инженерно-строительного института, Санкт-Петербургский политехнический университет Петра Великого, Санкт-Петербург
Политехническая ул., д. 29Б, г. Санкт-Петербург, 195251, Российская Федерация
e-mail: zimin_sergei@mail.ru
Рецензия
Для цитирования:
Зимин С.С. Напряженно-деформированное состояние каменных крестовых сводов. Вестник НИЦ «Строительство». 2024;43(4):182-194. https://doi.org/10.37538/2224-9494-2024-4(43)-182-194. EDN: DRQFSH
For citation:
Zimin S.S. Stress-strain state of stone cross vaults. Bulletin of Science and Research Center of Construction. 2024;43(4):182-194. (In Russ.) https://doi.org/10.37538/2224-9494-2024-4(43)-182-194. EDN: DRQFSH


























