Содержание
Перейти к:
К вопросу создания верификационной модели для расчета кессонного железобетонного перекрытия в вычислительном комплексе SCAD
https://doi.org/10.37538/2224-9494-2022-1(32)-128-140
Аннотация
Введение. Вопросами аналитических и компьютерных расчетов железобетонных кессонных перекрытий занимались многие исследователи. Анализ полученных ими данных показывает, что усилия в балках в зависимости от созданной конечно-элементной модели могут существенно отличаться. Некоторые модели не позволяют корректно подобрать армирование балок в автоматическом режиме вычислительного комплекса.
Целью данной работы является создание компьютерной модели кессонного перекрытия усилия, армирование и прогибы в балках которого можно сравнить с данными аналитического расчета, выполненного в соответствии с нормативными требованиям.
Материалы и методы. В соответствии с методом конечных элементов наиболее точной является модель, состоящая из конечных элементов стержневого типа. Наиболее простой аналитический расчет можно осуществить для кессонной конструкции квадратной в плане, с квадратными кессонами, так как упрощается определение коэффициентов, от которых зависит распределение нагрузки на балки. В связи с этим в качестве методики авторами разработаны три стержневые конечно-элементные модели перекрытия квадратного в плане 9,0 х 9,0 м с квадратными кессонами 0,9 х 0,9 м. Первая модель представляет собой стержневые конечные элементы таврового сечения с непосредственным приложением к ним погонной нагрузки, собираемой с отсеков по закону треугольника. Вторая и третья модели отличаются от первой способом приложения нагрузки на гибкий конечный элемент оболочечного типа регулярного и хаотичного разбиений.
Результаты. Результаты расчетов показали, что компьютерные модели достоверно отражают напряженное состояние балок кессонного перекрытия при сравнении с расчетом, выполненным аналитическим способом. Отклонения по изгибающим моментам не превышают +5 %.
Выводы. Разработанные конечно-элементные модели SCAD позволяют достоверно определить усилия и провести расчет железобетонных балок кессонного перекрытия по первой и второй группам предельных состояний, сравнить полученные данные с аналитическим расчетом, выполненным в соответствии с нормативными требованиями. Предлагаемые модели можно использовать при верификационных расчетах моделей перекрытия, состоящих из разных типов конечных элементов.
Ключевые слова
железобетонные кессонные перекрытия,
конечно-элементная расчетная модель,
верификационные вычисления,
изгибающие моменты,
поперечные силы
Для цитирования:
Мозголов М.В., Козлова Е.В. К вопросу создания верификационной модели для расчета кессонного железобетонного перекрытия в вычислительном комплексе SCAD. Вестник НИЦ «Строительство». 2022;32(1):128-140. https://doi.org/10.37538/2224-9494-2022-1(32)-128-140
For citation:
Mozgolov M.V., Kozlova E.V. Creation of a SCAD verification model for the design calculations of a reinforced-concrete waffle slab floor system. Bulletin of Science and Research Center of Construction. 2022;32(1):128-140. (In Russ.) https://doi.org/10.37538/2224-9494-2022-1(32)-128-140
Введение
Одним из эффективных с конструктивной точки зрения и необычным по архитектуре является часторебристое перекрытие кессонного типа [1–7]. В последнее время с появлением новых технологий проектного, расчетного и производственного направлений интерес к кессонным перекрытиям возобновился. Распространение получают опалубочные системы SKYDOME, NAUTILUS, HOLEDECK, U-Boot Beton и др.
В связи с широким внедрением в области строительства BIM-технологий, утвержденных на законодательном уровне (СП 333.1325800.2020 Информационное моделирование в строительстве. Правила формирования информационной модели объектов на различных стадиях жизненного цикла), и массовым переходом инженеров на компьютерные методы расчета, о проектировании строительных конструкций заговорили в форме 3D-моделей, состоящих из различных конечных элементов (стержней, плит, оболочек, объемных тел, специальных конечных элементов). Монолитное балочное железобетонное перекрытие можно смоделировать на ЭВМ различными способами [8–17]. При получении армирования конструкции в автоматическом режиме вычислительного комплекса все модели имеют свои достоинства и недостатки, некоторые из них не позволяют корректно подобрать армирование балок по причине возникновения проблем, связанных со стыковкой конечных элементов разного типа.
При выполнении расчета инженер должен быть уверен, что его условная расчетная схема соответствует проектируемой конструкции, удовлетворяет требованиям надежности, экономичности и безопасности. Ошибочность принятого решения может привести в лучшем случае к необоснованному перерасходу материала, а в худшем – к снижению надежности конструкции или ее разрушению. В работе [17] представлены значения изгибающих моментов в балках кессонного перекрытия прямоугольного вплане 11,55 × 9,0 м с прямоугольными кессонами 1,65 × 1,5 м, рассчитанные при помощи различных компьютерных моделей вычислительного комплекса SCAD. Полученные данные сравниваются с данными аналитического расчета [4], при этом различия в изгибающих моментах составляют от –6,3 до +61,9 %. Значительные отклонения усилий в балках кессонных перекрытий, найденные аналитическими и компьютерными методами, отмечаются в работах [6][7].
Цель
Целью данной работы является создание простой и понятной инженеру компьютерной конечно-элементной расчетной модели кессонного перекрытия, усилия в балках которого можно сравнить с усилиями аналитического расчета и в дальнейшем выполнить расчет конструкции по первой и второй группам предельных состояний в соответствии с требованиями норм. Впоследствии использовать данную модель в качестве верификационной.
Материалы и методы
С методикой аналитического расчета кессонных перекрытий, опертых по контуру, можно познакомиться в работах [1–7].
Например, в расчетной схеме, моделирующей балочное перекрытие, состоящей из пластинчатых (полка) и стержневых (ребро) конечных элементов, соединенных жесткими вставками, в стержнях кроме изгибающих моментов и поперечных сил возникают значительные продольные усилия и элемент при подборе арматуры будет сконструирован как внецентренно-растянутый, а подобранная арматура в нем будет распределена по всему периметру сечения [10][11]. Распределенной по сечению ребра получается арматура и в моделях, составленных из оболочечных конечных элементов [15].
Наиболее простой аналитический расчет можно осуществить для кессонной конструкции квадратной в плане, с квадратными кессонами, так как упрощается определение коэффициентов, от которых зависит распределение нагрузки на балки. При одинаковой ортогональной жесткости перекрытия нагрузка на балки распределяется поровну.
Для анализа выбрано перекрытие квадратное в плане 9,0 × 9,0 м с квадратными кессонами 0,9 × 0,9 м, конструируемое из элементов системы SKYDOME (купол H 400, перекладина Т 200, толщина полки 80 мм) [19], работающее на равномерно-распределенную нагрузку q = 1,5 Т/м2 с шарнирным опиранием по контуру (рис. 1). Собственный расчетный вес перекрытия составляет: gr = (0,222 + 0,08) • 2500 • 1,1 = 831 кг/м2. В методе конечных элементов считается, что точные решения получаются для стержней постоянного сечения по их длине [14]. Поэтому в соответствии с геометрией перекрытия в качестве конечного элемента принят стержень – тавровая балка высотой 480 мм, с шириной ребра 200 мм, толщиной полки 80 мм, шириной полки 900 мм из бетона класса В25. В часторебристом перекрытии для балок одного направления балки другого направления являются для первых ребрами жесткости, и в соответствии с требованиями п. 8.1.11 СП 63.13330.2018 «Бетонные и железобетонные конструкции. Основные положения» в расчете мы должны учитывать всю ширину полки.
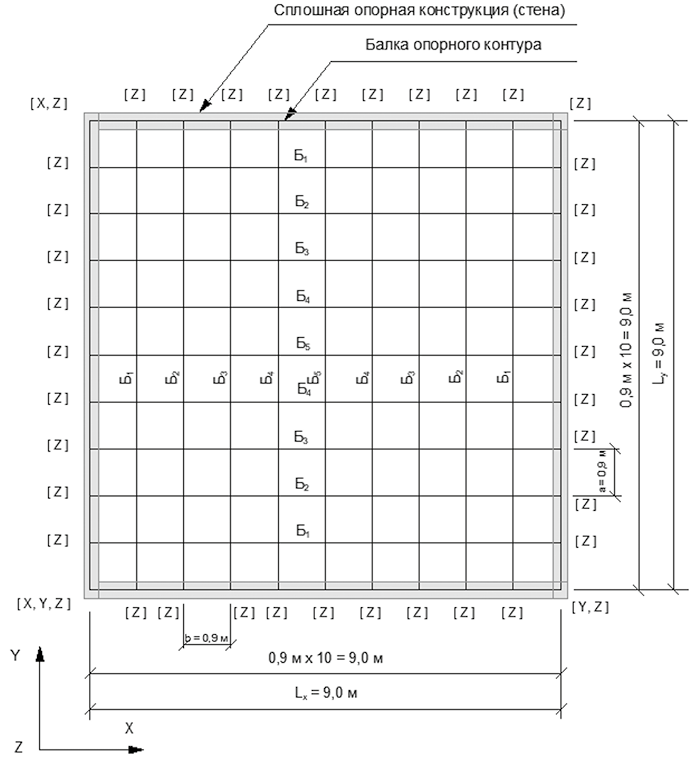
Рис. 1. Схема кессонного перекрытия. Б1, Б2, Б3, Б4, Б5 – рассчитываемые балки.
[X, Y, Z] – связи, установленные в узлах балки опорного контура
Fig. 1. Schematic of the waffle slab floor system. B1, B2, B3, B4, and B5 – analyzed beams.
[X, Y, Z] – connections established in the beam nodes of the support contour
Были созданы три компьютерные модели, отличающиеся в способе приложения нагрузки. В первой модели погонная нагрузка прикладывалась непосредственно на балки по закону треугольника [3], собираемая с двух смежных отсеков: q = 2 • 1,5 • 0,9/2 = 1,35 Т/м.
Во второй модели равномерно-распределенная нагрузка прикладывалась на гибкую плиту из 41 прямоугольного конечного элемента оболочки, толщиной 1 см с модулем упругости материала E = 1 Т/м2, коэффициентом Пуассона μ=0 и коэффициентом линейного расширения материала α = 1,0 • 10−5 0С−1, установленную в центре тяжести балок. Разбиение отсеков было регулярным, с шагом 5 × 5 элементов. Известно, что в методе конечных элементов сходимость данных по поперечной силе элементов пластинчатого типа может не обеспечиваться [13][14]. Поэтому с целью изучения сходимости результата и возможности применения для сбора нагрузок гибкой плиты различной геометрии, например в треугольных и косых кессонах, в третьей модели плита выполнена из 42 треугольных конечных элементов оболочки размером 0,3 м с хаотичным петч-разбиением [14]. Расчет выполнялся всеми методами, предусмотренными ВК SCAD. При выполнении расчетов в протоколе предупреждение о геометрически-изменяемой системе отсутствовало.
В соответствии с требованиями п. 6.2.5 СП. 430.1325800.2018 «Монолитные конструктивные системы. Правила проектирования» и п. 2.1.1.1. Методического пособия [18] для учета ползучести бетона и наличия трещин при расчете балок компьютерных моделей начальный модуль упругости бетона умножался на коэффициент 0,2 для участков с трещинами (пролетные балки) и 0,3 – для участков без трещин (балки опорного контура).
Выполним аналитический расчет. Так как конструкция симметричная в плане относительно осей X и Y, рассматриваем 5 балок: Б1, Б2, Б3, Б4 Б5. Расчет начинаем с определения q1 и q2 – долей равномерно-распределенной нагрузки q, действующей наперекрытие и приходящиеся на балки пролетов Ly и Lx. Вычисляем коэффициенты К1 и К2:
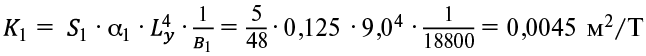, (1)
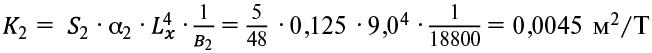, (2)
где В1, В2 – жесткость перекрытия вдоль осей Y и X.
В нашем случае:
B1 = B2 = 0,2 • Eb • I = 18800 Тм2, (3)
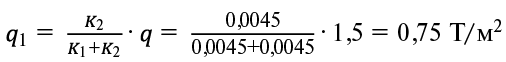, (4)
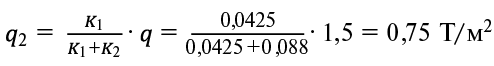. (5)
Расчет начинаем с центральной балки Б5, так как ее усилия являются базовыми для остальных балок. Определяем максимальный изгибающий момент в середине пролета и поперечную силу в приопорной зоне.
Балка Б5
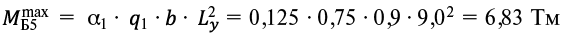, (6)
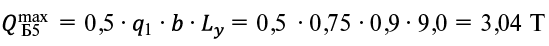. (7)
Балка Б4
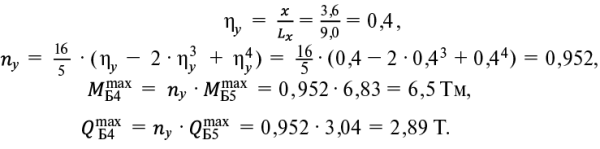(8, 9, 10, 11)
Балка Б3
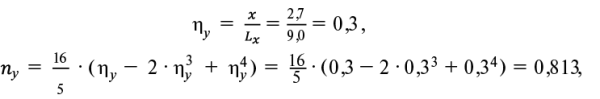(12, 13)
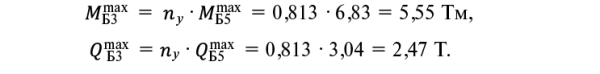(14, 15)
Балка Б2
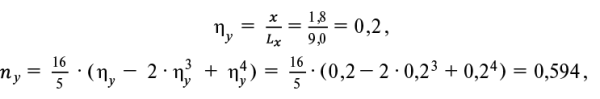(16, 17)
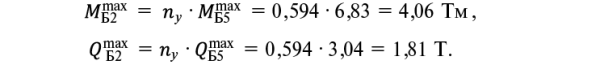(18, 19)
Балка Б1
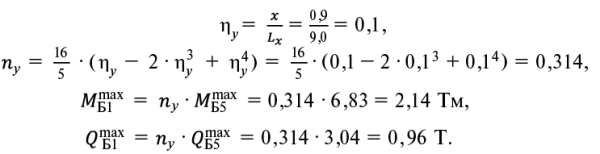(20, 21, 22, 23)
С целью сравнения методики компьютерного определения перемещения конструкции с аналитической методикой найдем ее по общим правилам строительной механики.
Максимальное перемещение центральной шарнирно-опертой балки Б5 модели № 1 SCAD определяется по формуле:
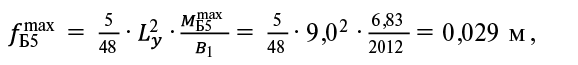(24)
где В1 – жесткость балки вдоль оси Y.
B1 = 0,2 • Eb • I = 2012 Тм2. (25)
Перемещение узла модели № 1 SCAD f = 30,5 мм.
Результаты
Полученные данные при расчете конструкции в вычислительном комплексе SCAD представлены на рис. 2–6.
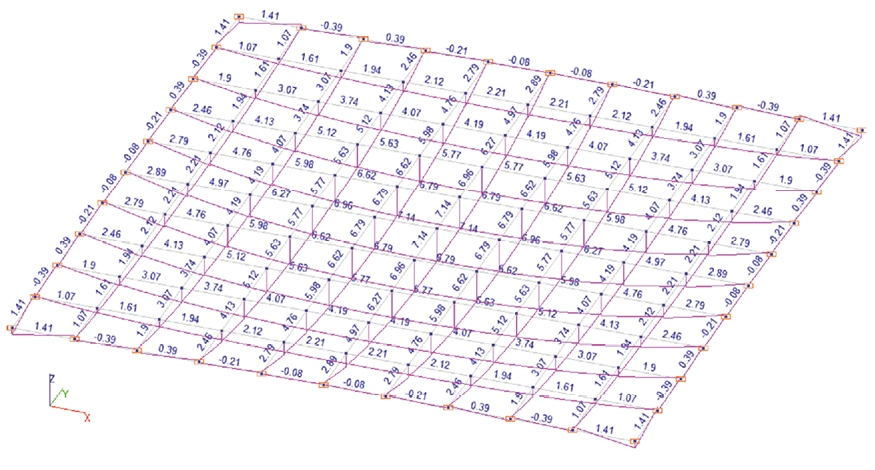
Рис. 2. Эпюры изгибающих моментов Му, Тм в балках модели № 1 SCAD
Fig. 2. Diagrams of bending moments Му and Tm in the beams of SCAD model No. 1
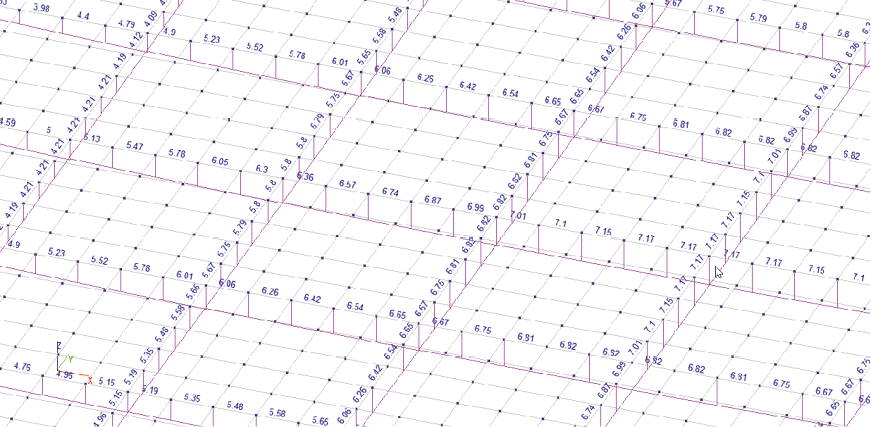
Рис. 3. Эпюры изгибающих моментов Му, Тм в балках модели № 2 SCAD.
Фрагмент центральной части перекрытия
Fig. 3. Diagrams of bending moments Му and Tm in the beams of SCAD model No. 2.
Central part of the floor system
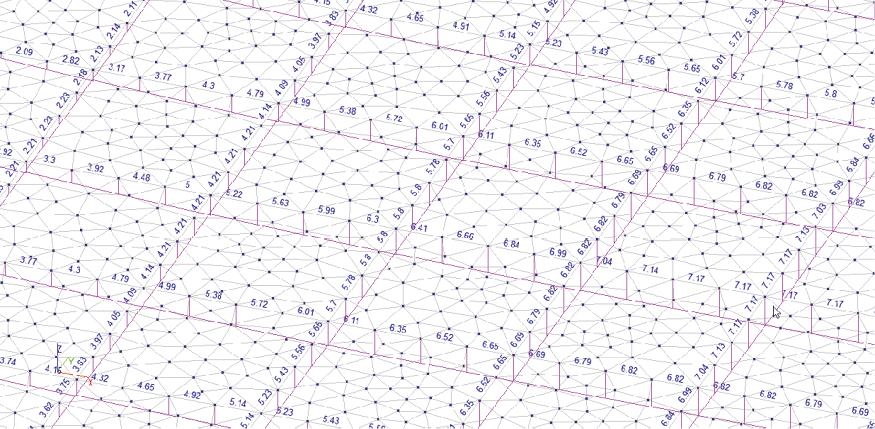
Рис. 4. Эпюры изгибающих моментов Му, Тм в балках модели № 3 SCAD.
Фрагмент центральной части перекрытия
Fig. 4. Diagrams of bending moments Му and Tm in the beams of SCAD model No. 3.
Central part of the floor system
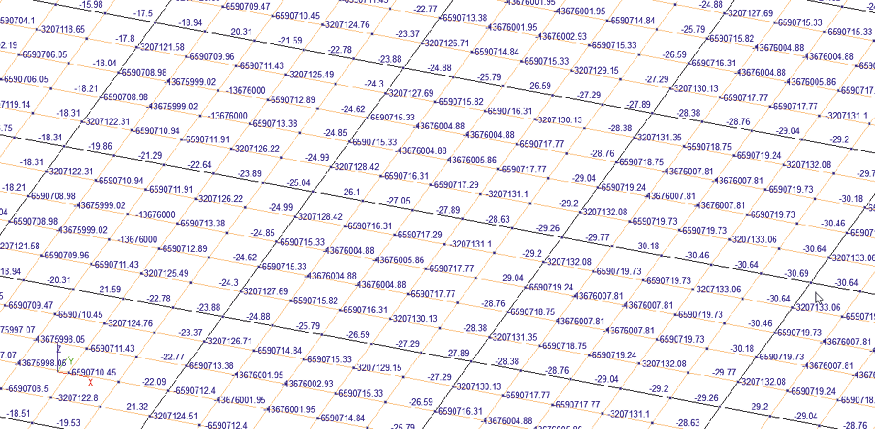
Рис. 5. Значения перемещений f, мм, узлов модели № 2 SCAD.
Фрагмент центральной части перекрытия
Fig. 5. Displacements f, mm of nodes in SCAD model No. 2.
Central part of the floor system
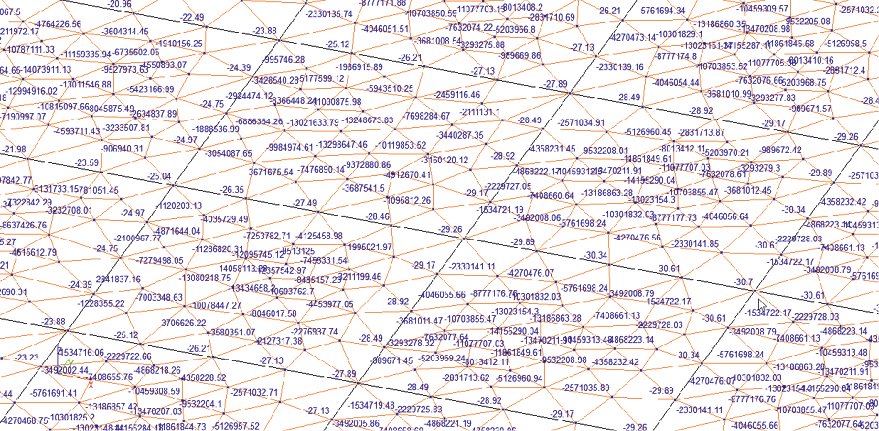
Рис. 6. Значения перемещений f, мм, узлов модели № 3 SCAD.
Фрагмент центральной части перекрытия
Fig. 6. Displacements f, mm of nodes in SCAD model No. 3.
Central part of the floor system
Данные аналитического расчета и компьютерных моделей представлены в табл. 1.
Таблица 1
Сравнение значений изгибающих моментов, поперечных сил и перемещений
в балках кессонного перекрытия 9,0 × 9,0 м, полученные аналитическим методом
и при помощи компьютерных моделей вычислительного комплекса SCAD
Table 1
Comparison of bending moments, shear forces, and displacements in the beams
of the waffle slab floor system (9.0 × 9.0 m) obtained using the analytical method and SCAD models
Балка | Аналитический расчет (эталон) | Модель № 1 SCAD(нагрузка на стержни) | Модель № 2 SCAD(нагрузка на 41 КЭ) | Модель № 3 SCAD(нагрузка на 42 КЭ) | |||||||
Мy Тм | Qz Т | Мy Тм | Qz Т | f мм | Мy Тм | Qz Т | f мм | Мy Тм | Qz Т | f мм | |
Б1 | 2,14 100 % | 0,96 100 % | 2,21 103 % | 1,64 171 % | 9,7 | 2,2 103 % | 1,66 173 % | 9,71 | 2,21 103 % | 1,66 173 % | 9,71 |
Б2 | 4,06 100 % | 1,81 100 % | 4,19 103 % | 2,75 152 % | 18,2 | 4,21 103 % | 2,74 151 % | 18,34 | 4,21 103 % | 2,75 152 % | 18,35 |
Б3 | 5,55 100 % | 2,47 100 % | 5,77 104 % | 3,44 139 % | 24,9 | 5,8 105 % | 3,44 139 % | 25,04 | 5,8 105 % | 3,44 139 % | 25,04 |
Б4 | 6,5 100 % | 2,89 100 % | 6,79 105 % | 3,84 133 % | 29,1 | 6,82 105 % | 3,84 133 % | 29,26 | 6,82 105 % | 3,84 133 % | 29,26 |
Б5 | 6,83 100 % | 3,04 100 % | 7,14 105 % | 3,98 131 % | 30,5 | 7,17 105 % | 3,98 131 % | 30,69 | 7,17 105 % | 3,99 131 % | 30,7 |
Проверим равновесие расчетных схем. Грузовая площадь балок
A = 9,0 • 9,0 − (0,9 • 0,45 • 0,5 • 40) = 72,9 м2.
Суммарная нагрузка на балки F = q • A = 1,5 • 72,9 = 109,35 Т.
Аналитический расчет: Q = 0,96 • 8 + 1,81 • 8 + 2,47 • 8 + 2,89 • 8 + 3,04 • 4 = 77,2 T.
Ошибка 109,35 – 77,2 = 32,15 Т, равновесие не соблюдается;
Модель № 1 SCAD. Q = 1,64 • 8 + 2,75 • 8 + 3,44 • 8 + 3,84 • 8 + 3,98 • 4 = 109,28 T.
Совпадение 100 %, равновесие соблюдается.
Выводы
- Предлагаемые расчетные модели вычислительного комплекса SCAD достоверно отражают напряженное состояние балок кессонного перекрытия квадратного в плане с квадратными кессонами при сравнении с расчетом, выполненным аналитическим способом. Отклонения по изгибающим моментам не превышают +5 %.
- Аналитический метод определения усилий в балках кессонных перекрытий имеет погрешность, об этом свидетельствует распределение поперечных сил. Равновесие аналитической расчетной схемы не соблюдается, равновесие компьютерных моделей соблюдается.
- При расчете кессонных перекрытий в виде стержневой конечно-элементной компьютерной модели удобно использовать модель с приложением нагрузки на гибкую плиту, расположенную в центре тяжести сечения стержневого конечного элемента. В качестве гибкой плиты эффективно применять 41, 42, 44 конечный элемент оболочки с условными физическими характеристиками (толщина 1 см, модуль упругости E = 1 Т/м2, коэффициент Пуассона μ = 0, коэффициент линейного расширения материала α = 1,0 • 10−5 0С−1), обеспечивающими ему большую гибкость. Гибкая плита работает по биссектрисной схеме излома, передает нагрузку на несущие конструкции по закону треугольника, ее жесткость не влияет на их напряженно-деформированное состояние.
- Созданные в вычислительном комплексе SCAD конечно-элементные модели позволяют провести расчет железобетонных балок кессонного перекрытия по первой и второй группам предельных состояний, полученные данные армирования, ширины раскрытия трещин и прогибов сравнить с «ручным» аналитическим расчетом, выполненным в соответствии с нормативными требованиями. Предлагаемые стержневые конечно-элементные модели как наиболее точные метода конечных элементов можно использовать при верификационных вычислениях моделей перекрытия, состоящих из разных типов конечных элементов (стержневых, плитных, оболочечных, их сочетаний). Недостатком предложенных конечно-элементных моделей является отсутствие расчетных данных для полки кессонной конструкции, а также невозможность приложения нагрузки от собственного веса в автоматическом режиме вычислительного комплекса.
- Гибкий конечный элемент оболочечного типа с условными характеристиками удобно использовать при сборе нагрузок на стержневые расчетные схемы сложной конфигурации.
Список литературы
1. Расчет и конструирование частей жилых и общественных зданий: справочник проектировщика / П.Ф. Вахненко, В.Г. Хилобок, Н.Т. Андрейко, М.Л. Яровой. - Киев: Будiвельник, 1987. - 424 с.
2. Давыдов С.С. Руководство по железобетонным и каменным конструкциям / С.С. Давыдов, А.С. Жиров, И.И. Иванова. - Москва: МИИТ, 1975. - 248 с.
3. Иванов-Дятлов И.Г. Железобетонные конструкции / И.Г. Иванов-Дятлов. - Москва, Ленинград: Министерство коммунального хозяйства РСФСР, 1950. - 296 с.
4. ЛиновичЛ.Е. Расчет и конструирование частей гражданских зданий / Л.Е. Линович. - Киев: Будiвельник, 1972. - 664 с.
5. Железобетонные конструкции / И.И. Улицкий, С.А. Ривкин, М.В. Самолетов [и др.]. - Киев: Будiвельник, 1972. - 992 с.
6. Малахова А.Н. Монолитные кессонные перекрытия зданий / А.Н. Малахова // Вестник МГСУ. - 2013. -№ 1. - С. 79-86.
7. Мозголов М.В. Об эффективности косых кессонных железобетонных перекрытий / М.В. Мозголов, А.В. Туранова // Градостроительство и архитектура. - 2021. - Т. 11, № 3. - С. 20-25. https://doi.org/10.17673/Vestnik.2021.03.03
8. Алямовский А.А. Инженерные расчеты в SolidWorksSimulation / А.А. Алямовский. - Москва: ДМК Пресс, 2019. - 464 с.
9. Проектирование несущих конструкций многоэтажного каркасного здания / С.В. Горбатов, О.В. Кабанцев, А.И. Плотников [и др.]. - Москва: АСВ, 2016. - 196 с.
10. Расчет и проектирование конструкций высотных зданий из монолитного железобетона / А.С. Городецкий, Л.Г. Батрак, Д.А. Городецкий [и др.]. - Киев: Факт, 2004. - 106 с.
11. Городецкий А.С. Компьютерные модели конструкций / А.С. Городецкий, И.Д. Евзеров. - Киев: Факт, 2005. - 344 с.
12. Городецкий А.С. Компьютерное моделирование в задачах строительной механики / А.С. Городецкий, М.С. Барабаш, В.Н. Сидоров. - Москва: АСВ, 2016. - 337 с.
13. SCADOffice. Версия 21. Вычислительный комплекс SCAD ++ / В.С. Карпиловский, Э.З. Криксунов, A.А. Маляренко [и др.]. - Москва: СКАД СОФТ, 2015. - 848 с.
14. Перельмутер А.В. Расчетные модели сооружений и возможность их анализа / А.В. Перельмутер, B.И. Сливкер. - Москва: ДМК Пресс, 2007. - 600 с.
15. Скорук Л. Поиск эффективных расчетных моделей ребристых железобетонных плит и перекрытий / Л. Скорук // CADmaster. - 2004. - № 3. - С. 78-83.
16. Вычислительный комплекс SCAD в учебном процессе. Статический расчет / А.А. Семенов, А.И. Габитов, А.А. Маляренко [и др.]. - Москва: АСВ, СКАД СОФТ, 2016. - 242 с.
17. Лоскутов И.С. Монолитные железобетонные кессонные перекрытия [Электронный ресурс] / И.С. Лоскутов // DWG.ru: Железобетонные конструкции. - URL: https://dwg.ru/lib/2046 (дата обращения: 24.10.2021).
18. Плоские безбалочные железобетонные перекрытия: методическое пособие [Электронный ресурс]. -Москва, 2017. - URL: https://www.faufcc.ru/upload/methodical_materials/mp60_2017.pdf (дата обращения 24.10.21).
19. Многоразовая опалубка из ABS - пластика для ребристых плит перекрытия. Skydome. Система для двунаправленных перекрытий [Электронный ресурс]. URL: https://www.geoplastglobal.com/sites/default/files/katalog_skydome_ru.pdf (дата обращения 24.10.21).
Об авторах
М. В. Мозголов
Коломенский институт (филиал) ФГБОУ ВО «Московский политехнический университет»
Россия
Россия
Мозголов Михаил Валентинович - кандидат технических наук, доцент кафедры «Строительное производство».
ул. Октябрьской революции, д. 408, Коломна, 140402.
Е. В. Козлова
Коломенский институт (филиал) ФГБОУ ВО «Московский политехнический университет»
Россия
Россия
Козлова Елизавета Вадимовна - студент 3-го года обучения направления «Строительство».
ул. Октябрьской революции, д. 408, Коломна, 140402.
Дополнительные файлы
Рецензия
Для цитирования:
Мозголов М.В., Козлова Е.В. К вопросу создания верификационной модели для расчета кессонного железобетонного перекрытия в вычислительном комплексе SCAD. Вестник НИЦ «Строительство». 2022;32(1):128-140. https://doi.org/10.37538/2224-9494-2022-1(32)-128-140
For citation:
Mozgolov M.V., Kozlova E.V. Creation of a SCAD verification model for the design calculations of a reinforced-concrete waffle slab floor system. Bulletin of Science and Research Center of Construction. 2022;32(1):128-140. (In Russ.) https://doi.org/10.37538/2224-9494-2022-1(32)-128-140
Просмотров:
640
Послать статью по эл. почте 