Перейти к:
Оптимальный выбор расположения опор в задаче устойчивости прямоугольной пластинки при воздействии температурного поля
https://doi.org/10.37538/2224-9494-2022-3(34)-45-53
Аннотация
Введение. Тонкостенные пластинки как элементы конструкции имеют широкое применение в современном строительном деле, машиностроении, судостроении, самолетостроении и других областях современной техники. В срединной плоскости пластинки действуют равномерно распределенные нормальные механические усилия интенсивностью σφ и температурное поле одновременно. В области исследования прочности и устойчивости прямоугольной пластинки следует отметить работы С.П. Тимошенко [1], С.А. Амбарцумяна [2] и др. В области оптимального проектирования тонкостенных элементов конструкций, а именно в задачах термоупругой устойчивости пластинки, недостаточно исследованы вопросы определения оптимального расположения опор. Вопросы оптимального расположения опор в пластинки рассматривались в работах В.Ц. Гнуни [3], М.В. Белубекяна [4] и А.В. Элояна [5, 6]. При одновременном воздействии нормальных механических усилий и температурного поля на прямоугольную пластинку ставится задача оптимального выбора параметра с, характеризующего расположение поперечных опор по длине пластинки, обеспечивающего наибольшее значение критической нагрузки.
Цель. Вычисление оптимальных значений параметра α = c/a и соответствующих значений σ̅, h̅ для различных отношений сторон λ = a/b пластинки и при заданных значениях температуры.
Материалы и методы. В работе были применены упругие изотропные пластинки и определено наибольшее значение критической нагрузки.
Результаты и выводы. Как показывают расчеты, оптимальное расположение опор для значения λ = a/b – 1/2,1 получается при σ̅ = 3β и зависит от температуры пластины. Наибольшее значение критической нагрузки для всех случаев отношения сторон пластинки получается при σ̅ = 3β, h̅ = 0,01, w* = 1,772, α = 0,37, Т = 300 °С, обеспечивающих наибольшее значение критической нагрузки.
Для цитирования:
Элоян А.В., Карапетян Д.К., Матевосян Г.М., Карапетян Р.К. Оптимальный выбор расположения опор в задаче устойчивости прямоугольной пластинки при воздействии температурного поля. Вестник НИЦ «Строительство». 2022;34(3):45-53. https://doi.org/10.37538/2224-9494-2022-3(34)-45-53
For citation:
Eloyan A.V., Karapetyan J.K., Matevosyan G.M., Karapetyan R.K. Optimal support positioning of a rectangular plate in a stability problem under temperature field exposure. Bulletin of Science and Research Center of Construction. 2022;34(3):45-53. (In Russ.) https://doi.org/10.37538/2224-9494-2022-3(34)-45-53
Введение
Тонкостенные пластинки как элементы конструкции имеют широкое применение в современном строительном деле, машиностроении, судостроении, самолетостроении и других областях современной техники. В современных конструкциях большое практическое применение имеют упругие изотропные и анизотропные пластинки, находящиеся под равномерно распределенные усилиям с интенсивностью σφ. В области исследований прочности и устойчивости прямоугольной пластинки следует отметить работы С.П. Тимошенко [1], С.А. Амбарцумяна [2] и др. В области оптимального проектирования тонкостенных элементов конструкций, а именно в задачах термоупругой устойчивости пластинки, недостаточно исследованы вопросы определения оптимального расположения опор. Вопросы оптимального расположения опор в пластинке рассматривались в работах В.Ц. Гнуни [3], М.В. Белубекяна [4] и А.В. Элояна [5][6].
Решение задачи
Пусть прямоугольная пластинка размерами x ∈ [–a/2; a/2], y ∈ [0, b], z ∈ [−h/2; z/2] отнесена к прямоугольной системе декартовых координат Oxyz так, что координатная плоскость z = 0 совпадает со срединной плоскостью пластинки. Предполагается, что продольные края пластинки свободно оперты, а поперечные опоры расположены на расстоянии c от срединной линии x = 0 пластинки, т. е. по направлениям x = –c и x = +c (рис. 1).
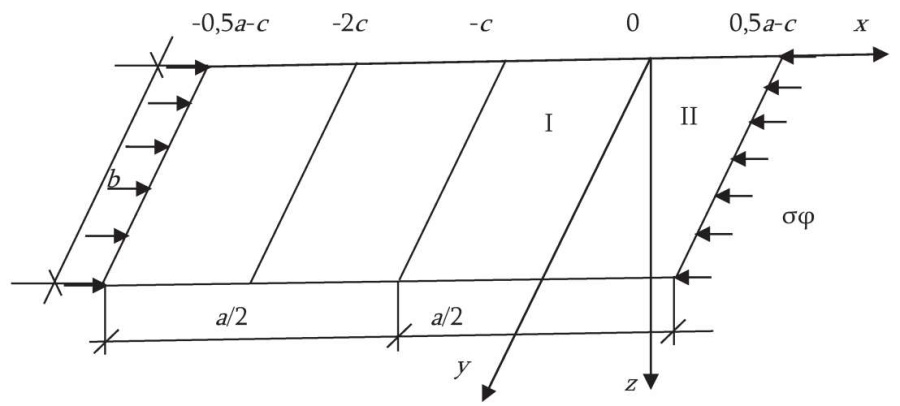
Рис. 1. Расчетная схема пластинки
Fig. 1. Design model of a plate
В срединной плоскости пластинки по направлениям ее сторон 0x действуют равномерно распределенные нормальные механические усилия интенсивностью σφ и температурное поле.
При одновременном воздействии нормальных усилий и температурного поля ставится задача оптимального выбора параметра c, характеризующего расположение поперечных опор, обеспечивающее наибольшее значение критической нагрузки.
Ввиду симметрии пластинки относительно плоскости (x = 0) исследуется случай симметричной потери устойчивости и, следовательно, рассматривается устойчивость правой половины пластины 0 ≤ x ≤ 0,5a. При этом решаются дифференциальные уравнения устойчивости для каждого из участков 0≤ x ≤ с и −c ≤ x ≤ 0,5 a−c, учитывающие наличие стационарного температурного поля [4].
 (1)
(1)
Здесь 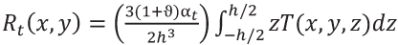 характеризует температурную нагрузку;
характеризует температурную нагрузку;
D = Eh3/12(1−ϑ2) – цилиндрическая жесткость пластинки;
E – модуль упругости;
ϑ – коэффициент Пуассона;
α – коэффициент температурного линейного расширения.
Выражения для моментов и перерезывающих усилий и влияние температуры (Re) не зависит от координат. В этом частном случае температура не входит в уравнение изгиба (1) и в формулы для перерезывающих усилий из (1). Вследствие температуры появляются изгибающие моменты, что видно из выражений (2) для Mx(k), My(k).
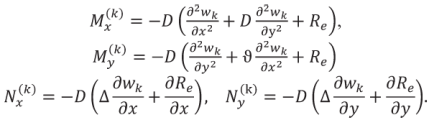 (2)
(2)
В дальнейшем предполагается, что кромки пластинки y = 0 и y = b свободно оперты (шарнирно закреплены, т. е. имеют место граничные условия)
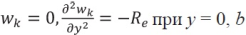 (3)
(3)
В этом случае при условиях (2), с учетом Re = 0 решение уравнения (1) удобнее представить в виде
wk(x,y)=w̅k(x,y)+wt
Таким образом, задача приводится к решению уравнения
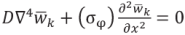 (4)
(4)
при граничных условиях
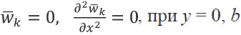 (5)
(5)
Допустим, что изменение температуры по толщине пластинки следует линейному закону и что в плоскостях, параллельных поверхностям пластинки, температура остается постоянной.
Тогда граничные условия задачи запишутся в виде:
Для шарнирного опирания на продольных краях y = 0, y = b.
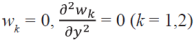 (6)
(6)
Для сопряжения термоупругого поля на поперечной опоре x = 0
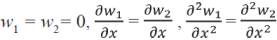 (7)
(7)
Для свободного края x = 0,5a – c
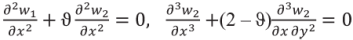 (8)
(8)
Для сопряжения термоупругого поля на поперечной плоскости симметрии (в случае симметричной потери устойчивости) x = −c
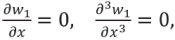 (9)
(9)
Допустим, что изменение температуры по толщине пластинки следует линейному закону и в плоскостях, параллельных поверхностям пластинки, температура остается постоянной.
В этом случае
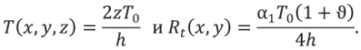
Прогибы пластинки wk(x, y), (k = 1,2) представляются в виде:
wk(x, y) = w̅k(x, y) + wt(x, y),
где w̅k(x, y) – прогибы на каждом из участков пластинки от равномерно распределенных нормальных усилий;
wt(x, y) – функция прогиба от действия температуры, которая предполагается изменяющейся по параболическому закону wt(x, y) = 0,5y (b – y)Rt.
Решение уравнения (4), удовлетворяющее условиям (5)–(7), принимается в виде:
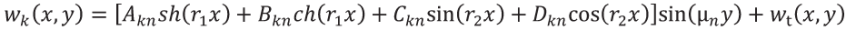 (10)
(10)
где
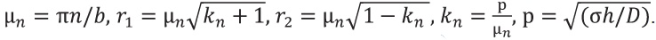
Удовлетворение граничных условий (5) – (7) приводит к системе однородных линейных уравнений относительно коэффициентов Akn, Bkn, Ckn, Dkn. Условия существования решения этой системы приводит к следующим уравнениям, где
 (11)
(11)
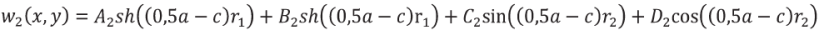 (12)
(12)

Задача оптимального расположения поперечных опор пластинки сводится к определению параметра α, обеспечивающего наибольшее значение критического напряжения при заданных габаритных размерах пластинки а/b, температуры и равномерно распределенных нормальных усилий.
Численные решения выполнены для случая, когда сжимающая нагрузка действует только в направлении оси Ox.
В уравнениях (11) и (12) приняты следующие обозначения α = c/a, (0 ≤ α ≤ 0,5).
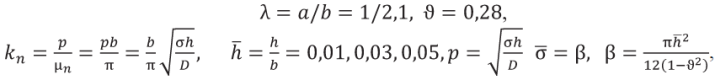
Вычислены оптимальные значения параметра α = c/a, соответствующие значениям σ̅, h̅ для различных отношений сторон λ = a/b пластинки и при заданных значениях температуры, изменяющейся от –50 до 300 °С, эти значения приведены в таблице.
Таблица
Table
h̅ | α | w* | Т° | λ | σ̅ |
0,01 | 0,33 | –0,021 | 300 | ½ | 1 |
0,03 | 0,33 | –0,017 | 300 | ½ | 1 |
0,05 | 0,33 | –0,012 | 300 | ½ | 1 |
0,01 | 0,37 | –1,772 | 300 | 1 | 1 |
0,03 | 0,37 | –1,347 | 300 | 1 | 1 |
0,05 | 0,37 | –1,128 | 300 | 1 | 1 |
0,01 | 0,33 | –0,012 | 200 | ½ | 1 |
0,03 | 0,35 | –8,1*10-3 | 200 | ½ | 1 |
0,05 | 0,35 | –8,5*10-3 | 200 | ½ | 1 |
0,01 | 0,37 | –1,135 | 200 | 1 | 1 |
0,03 | 0,37 | –1,083 | 200 | 1 | 1 |
0,05 | 0,37 | –1,027 | 200 | 1 | 1 |
0,01 | 0,35 | 4,1*10-3 | 100 | ½ | 1 |
0,03 | 0,35 | 4,7*10-3 | 100 | ½ | 1 |
0,05 | 0,35 | 4,9*10-3 | 100 | ½ | 1 |
0,01 | 0,37 | –0,595 | 100 | 1 | 1 |
0,03 | 0,37 | –0,582 | 100 | 1 | 1 |
0,05 | 0,37 | –0,538 | 100 | 1 | 1 |
0,01 | 0,35 | 1,8*10-3 | –50 | ½ | 1 |
0,03 | 0,35 | 1,9*10-3 | –50 | ½ | 1 |
0,05 | 0,35 | 2,5*10-3 | –50 | ½ | 1 |
0,01 | 0,37 | 0,282 | –50 | 1 | 1 |
0,03 | 0,37 | 0,271 | –50 | 1 | 1 |
0,05 | 0,37 | 0,264 | –50 | 1 | 1 |
Как показывают расчеты, оптимальное расположение опор для значений λ = a/b–1/2,1 получается при σ̅ = 3β и зависит от температуры пластины.
На рис. 2 показаны графики изменения критических напряжений в зависимости от расположения опор и температуры (параметр α = 0,37) при λ = a/b = 1.
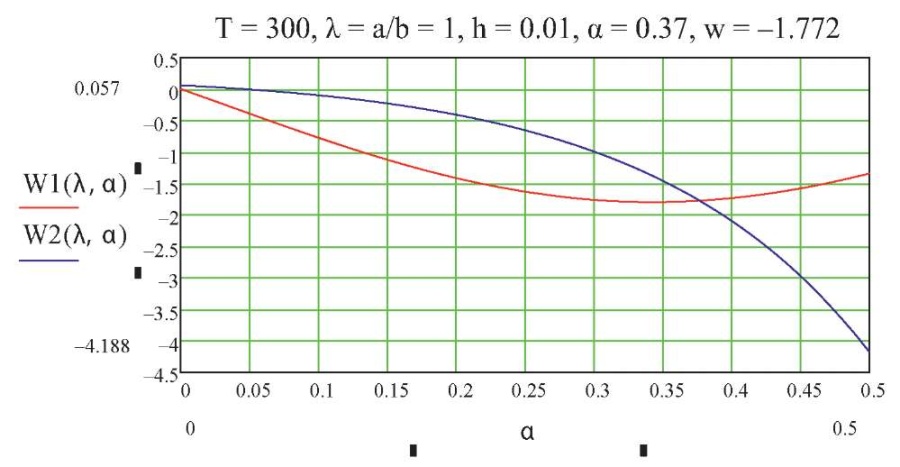
Рис. 2. График оптимального расположения поперечных опор
Fig. 2. Diagram of optimal positioning of transverse supports
Заключение
Как следует из таблицы, наибольшее значение критической нагрузки для всех случаев отношения сторон пластинки получается при σ̅ = 3β, h̅ = 0,01, w* = 1,772, α = 0,37, Т = 300 °С, обеспечивающее наибольшее значение критической нагрузки.
Список литературы
1. Тимошенко C.П. Прочность и колебания элементов конструкций. Москва: Физматгиз; 1975.
2. Амбарцумян С.А. Теория анизотропных пластинок. 2-е изд. Москва: Наука; 1987.
3. Гнуни В.Ц., Элоян А.В. Оптимальный выбор расположения опор в задаче изгиба прямоугольной пластинки. Изв. НАН PА. Механика. 2001;54(3):14–17.
4. Белубекян М.В., Саргсян М.Г., Саноян Ю.Г. Управление перемещениями в пьезопластинках с помощью электрического поля. Вестник Инженерной академии Армении. 2009;6(2):255–261.
5. Элоян А.В. Оптимальный выбор расположения опор в упругой изотропной прямоугольной пластинке при совместном воздействии поперечной нагрузки и температурного поля. Изв. НАН PА. Механика. 2013;66(4):17–22.
6. Элоян А.В. Оптимальный выбор расположения опор в задаче устойчивости прямоугольной пластинки // Вестник ГИУА. Сер. Моделирование, Оптимизация, Управление. 2008;1(11):112–116.
7. Белубекян Э.В., Элоян А.В. Оптимальный выбор расположения опор в задаче собственных колебаний упругой прямоугольной пластинки из композиционного материала. В: II Международная научно-техническая конференция «Архитектура и строительство – актуальные проблемы»: сборник докладов. Т. 1. Ереван – Джермук; 2010, с. 314–317.
Об авторах
А. В. ЭлоянАрмения
Асатур Ваноевич Элоян , канд. техн. наук, доцент НПУА РА, заведующий кафедрой инженерного строительства, старший научный сотрудник ИГИС НАН РА
Гюмри, 3115, ул. В. Саргсяна, 5
3115, Гюмри, ул. Мгера Мкртчяна, 2
тел.: (+37494) 58-31-67
Д. К. Карапетян
Армения
Джон Костикович Карапетян, канд. геол. наук, директор ИГИС НАН РА, заведующий лабораторией инженерной сейсмологии, анализа сейсмических воздействий и оценки сейсмической опасности, ассистент кафедры инженерного строительства НПУА РА
Гюмри, 3115, ул. В. Саргсяна, 5
3115, Гюмри, ул. Мгера Мкртчяна, 2
тел.: (+37494) 79-85-80
Г. М. Матевосян
Армения
Гурген Мишаевич Матевосян, младший научный сотрудник, аспирант
Гюмри, 3115, ул. В. Саргсяна, 5
тел.: (+37493) 58-13-13
Р. К. Карапетян
Армения
Роза Костиковна Карапетян, младший научный сотрудник
Гюмри, 3115, ул. В. Саргсяна, 5
тел.: (+37493) 64-33-03
Рецензия
Для цитирования:
Элоян А.В., Карапетян Д.К., Матевосян Г.М., Карапетян Р.К. Оптимальный выбор расположения опор в задаче устойчивости прямоугольной пластинки при воздействии температурного поля. Вестник НИЦ «Строительство». 2022;34(3):45-53. https://doi.org/10.37538/2224-9494-2022-3(34)-45-53
For citation:
Eloyan A.V., Karapetyan J.K., Matevosyan G.M., Karapetyan R.K. Optimal support positioning of a rectangular plate in a stability problem under temperature field exposure. Bulletin of Science and Research Center of Construction. 2022;34(3):45-53. (In Russ.) https://doi.org/10.37538/2224-9494-2022-3(34)-45-53


























