К определению размера полости в скальном массиве, необходимого для образования провала в вышележащей грунтовой толще

Наличие или образование внутри скального массива естественной полости, сохраняющей свою устойчивость, или устройство закрепленной подземной выработки не приводят к заметным последствиям в залегающей над этим массивом грунтовой толще, а оценка их параметров – вполне решаемая задача с использованием модели массива как сплошной деформируемой среды, обычно с применением программных конечно-элементных комплексов. Опасные и трудно прогнозируемые явления возникают, если полость в массиве, подстилающем толщу дисперсного грунта или трещиноватой породы, образуется непосредственно у его поверхности или на столь небольшом заглублении, что ее «кровля» может обрушиться, и полость окажется «открытой». Процессы потери устойчивости расположенной над полостью зоны толщи и разрывных перемещений материала в свободное пространство не могут быть корректно описаны в рамках механики сплошной среды, и для их описания и прогноза используются те или иные «инженерные» модели [1][2].

Наиболее простая из таких моделей – схема «провала», т. е. сдвига в полость объема грунта, имеющего условно вертикальную границу внутри массива. Прогноз размера в плане («диаметра») провала – одно из требований, обычно предъявляемых к анализу данных инженерно-геологических изысканий [2–5 и др.] в районах распространения карста. Часто под деформациями, вызванными образованием полостей, понимается именно появление провалов, и оценкой «диаметра» заканчивается характеристика опасности появления полости. Применяемые аналитические методики такой оценки чаще всего содержат [2][4][6][7 и др.] выделение в массиве грунта, расположенного над полостью, цилиндрического объема диаметром D и высотой H, равной мощности толщи. Обычно записываются выражения для сдвигающих T(D) и удерживающих N(D) усилий, приложенных к выделенному цилиндрическому объему, и определяется значение D = D_кр , при котором «коэффициент устойчивости» K(D) = N(D)/T(D) равен минимально допустимому значению k_уст, в существующих рекомендациях принимаемому равным единице. Далее (и об этом часто забывается) требуется сравнение полученного значения D_кр с «фактическим» или прогнозируемым к окончанию срока эксплуатации сооружения значением диаметра полости D_h. Провал с диаметром D_кр считается возможным, если D_кр ≤ D_h, и невозможным, если D_кр > D_h. Справедливость этой трактовки значений D, D_h и D_кр вполне понятна. По существу, она подразумевается и при изложении в [4] наиболее применяемой схемы определения «минимально возможного диаметра провала», где в п. 3.4 говорится, что записанная формула позволяет получить минимально возможный диаметр провала d₀ и что «поэтому для возникновения провала необходимо, чтобы размер полости в плане был не менее расчетного значения d₀». При изложении многочисленных вариантов определения диаметра провала на схемах, так же как на представленном рис. 1 из [4][8], D = D_h. Но тем не менее там же, в [4], рис. 1 называется «расчетная схема для определения диаметра провала», а в инженерно-геологических отчетах именно значение D_кр до сих пор принимается за «диаметр провала». При таком понимании прогнозируемый диаметр провала – показатель опасности – оказывается не только не зависящим от фактического размера полости, но при этом еще и увеличивающимся при «улучшении» условий, т. е. при росте мощности толщи над полостью и повышении прочности слагающих ее грунтов.

Прогноз деформаций массивов при образовании полостей любого генезиса должен начинаться с задания их размеров, и, хотя при современном уровне возможностей приходится принимать приближенные и иногда чисто «экспертные» оценки указанных размеров, этот путь представляется наиболее информативным. Предписанный в [5] порядок оценки размеров карстовых полостей исходит из того, что в основе их образования лежит процесс растворения карстующихся пород [9]. В [5][10] размер D_h карстовой полости определяется как

D_h = D₀ + v_s × T, (1)

где D₀ – начальный размер полости;

T – срок эксплуатации сооружения;

v_s – среднегодовая скорость растворения пород, определяемая по данным изысканий или назначаемая по приведенным в [5] диапазонам изменения v_s для пяти их разновидностей.

Указанные диапазоны ориентировочные, но их ранжирование отражает различие масштабов карстопроявлений над массивами пород с различной растворимостью.

Однако и при описанной «непротиворечивой» трактовке величины D_кр методы ее оценки нуждаются в корректировках, которым и посвящена настоящая статья. Например, задание в [4][6][7 и др.] значения коэффициента устойчивости k_уст равным единице противоречит практике геотехнических расчетов [12], где для учета недостаточной определенности исходных данных и несовершенства расчетных схем k_уст принимается в пределах 1,1…1,3. Другой аспект – необходимость различения ситуаций, где следует и где не следует учитывать влияние поверхностной дополнительной нагрузки на условия равновесия выделенного объема грунта. Отдельного рассмотрения требует учет особенностей работы нижнего «несущего» слоя грунтовой толщи.

, (4)

Z_ј ,(i = 1…M + 1) – отметки кровли (j = i) и почвы (j = i + 1) i-го слоя (Z₁ = 0, Z_M+1 = Σ^m_𝑖=1 h_i);

p_j– вертикальное давление в массиве на отметке Z_j ;

α(Z) ≤ 1 – функция, описывающая убывание по Z вертикальных напряжений в грунте на границе цилиндра;

k_z , k_g – принимающие значения 1 или 0 множители для учета или неучета влияния на вертикальные (k_z) и горизонтальные (k_g) напряжения в массиве.

Заметим, что во многих исследованиях [2][6 и др.] поверхностная нагрузка не учитывается, т. е. k_z = k_g = 0.

Напомним, что одним из основных (а фактически обязательных) противокарстовых конструктивных мероприятий, рекомендуемых в [5][10], является устройство плитных фундаментов. Поэтому нет необходимости рассматривать вариант «провала» под одиночным фундаментом, тем более что это обычно делается с явными ошибками в записи (не учитывается, что функция α(Z) должна относиться не к оси фундамента, а к боковой поверхности выделенного объема). В случае же в настоящее время практически безальтернативно применяемого в условиях карста плитного фундамента поверхностная нагрузка приложена в пределах зоны с размерами, существенно превосходящими «диаметр» провала. Тогда вертикальная нагрузка на поверхности, действующая и снаружи, и внутри контура «сдвигаемого» объема, не вносит дополнения в сдвигающее этот объем усилие, т. е. следует принимать k_z = 0. Влияние нагрузки p₀ должно учитываться только в величине давления на боковую поверхность сдвигаемого объема (k_g = 1). Кроме того, при приложении давления на большой площади можно пренебречь с учетом реального уровня достоверности задания других исходных параметров, «точным» описанием убывания по глубине вызываемых этим давлением напряжений и ограничиться линейной зависимостью

α(Z) =  (0 ≤ Z ≤ H). (5)

Хотя предлагаемые «корректировки» могут не очень сильно влиять на получаемые оценки D_кр, они позволяют существенно упростить расчеты, не пренебрегая рекомендациями [10].

Теперь запишем соотношение для определения R_кр

k_уст × 𝑇(𝑅) = 𝑄(𝑅) (6)

Подставляя в (6) соотношения (3), (4), получим

R_кр(k_уст) = 2k_уст (7)

При k_уст = 1 и k_z = 0, k_g = 0 получаем R_кр = 8,6 м, а при учете влияния поверхностной нагрузки (k_g = 1) на горизонтальные усилия на границе сдвигаемого цилиндра R_кр = 10,6 м. Заметим, что именно такого порядка величины радиуса провала приведены для условий H ≈ 30…40 м в работах [13][14 и др.], где обсуждаются методики, основанные на аналогичных схемах. Принять, как это часто делается, D = D_кр и получить приемлемое для проектировщиков значение D можно при мощности надкарстовой толщи менее 10 метров. Так, заменив h_i на уменьшенные значения hʹ_i = h_i /4, получим при k_g = 0 значение R_кр = 3,7 м, а при k_g = 1 значение R_кр = 5,2 м.

Оценим на рассматриваемом примере условия обоснованности часто используемого упрощения расчетов значения D_кр. Если считать грунт в пределах столба высотой H и радиусом R однородным с значениями γ, φ, C, полученными осреднением по Z (0 ≤ Z≤ H) то соответствующие формулам (2)–(4) соотношения запишутся в виде, аналогичном приведенному в [2], т. е.

Q = Q_c+Q_f = 2πRH [(k_g p₀ /2+γ×H/2)×μ×tg (φ))+C], (6)

где Q_c и Q_f – «удерживающие» усилия, вызываемые сцеплением и трением:

Q_c(R) = 2πRCH Q_f (R) = 2πR ((k_g p₀)/2+γH/2)μtg (φ), (7)

μ, p₀/2, γН/2 – осредненные по Z значения коэффициента бокового давления, вертикального напряжения в рассматриваемом «столбе» грунта от поверхностной нагрузки p₀ и от собственного веса грунта γ × Z. Решая относительно R уравнение T(R) = Q(R), получаем, что значение K = Q/T оказывается равным или меньшим k_уст, когда

Однако такое осреднение неэффективно, если попытаться, пусть в рамках также «инженерных» представлений, учесть в расчетной схеме реальную структуру грунтовой толщи. В частности, разрез, описанный кратко в табл. 1, – пример ситуации, когда непосредственно над полостью находится слой связного грунта с достаточно высоким значением С, выступающий в качестве «крепления» кровли полости. Чтобы понять, как в таких условиях может происходить формирование провала, упростим структурную модель многослойной толщи над полостью, используя показанную возможность замены ее части на эквивалентный слой. Верхнюю часть толщи, сложенную в основном слоями условно дисперсных грунтов, общей мощностью h_d заменим слоем грунта мощности h_d со средними по слоям i = 1… M-1 значениями γ_d , φ_d , С_d . Непосредственно над полостью залегает слой связного грунта мощностью h_c с характеристиками γ_c , φ_c , С_c.

Если в какой-то момент времени происходит увеличение размеров полости до критических значений или (как это бывает, по-видимому, чаще всего, и причем по техногенным причинам) происходит «снижение» показателей φ_c, С_c, то сначала разрушается находящийся над полостью слой связного грунта, а затем – перемещается в полость и объем грунта над этой полостью, с возможным образованием «провала» (рис. 2).

При отсутствии такого несущего слоя рост полости и увеличение ее открытого объема скорее приведут к постепенному непрерывному ее заполнению дисперсным материалом и росту «мульды оседания».

Для оценки возможности разрушения «несущего» слоя связного грунта используем две схемы определения нагрузки, действующей на его верхнюю границу, соответствующие «стандартным» методикам расчета так называемого диаметра карстового провала [2]. Одна из этих схем, по существу, та же схема «продавливания» (индекс B- «схема Бирбаумера» [2]) жесткого столба грунта, но примененная к «столбу» в двуслойной толще. Вертикальное давление σ_lB(R), передающееся от вышележащей толщи (условно однослойной) на нижний слой связного грунта, определим через разность «сдвигающего» T_d(R) и «удерживающего» Q_d(R) верхний слой «несвязного» грунта, т. е.

Эта схема заимствована из инженерной теории горного давления на крепь выработок в массивах трещиноватых пород [17], а формула (13) основана на анализе различных вариантов ее реализации. Примем давление от веса свода на кровле несущего слоя обрушения равномерно распределенным, определяемым по максимальной величине:

σ_lP(R) =  . (14)

Величины «удерживающих» несущий слой усилий Q_сB(R) и Q_сR(R) одинаковы, поскольку в рамках принимаемой в обеих схемах упрощенной модели деформирования грунтовой толщи одинаковы вертикальные напряжения и значения бокового давления в массиве.

Решение уравнения k_устT_cP(R) = Q_сP(R) при k_уст= 1 дает R^P_кр = 7,67 м. Видно, что за счет того, что σ_lp(R) > σ_lB (R), значение критического размера полости, при котором может произойти провал, прогнозируется по «схеме Протодьяконова» заметно меньшим (почти на 40 %), чем при «схеме Бирбаумера» (R^В_кр = 10,75 м). В качестве значения R_кр, определенного из обычного условия «среза» цилиндрического грунтового объема, следует принимать величину R^s_кр = min(R^B_кр, R^P_кр).

Но потеря устойчивости слоя связного грунта может произойти также от действия возникающих при его изгибе растягивающих напряжений в определенных зонах его нижней и верхней поверхностей. Устойчивость слоя над выработанным пространством в условиях плоской задачи с помощью исследования «балочного эффекта» предложено оценивать в [15]. Здесь такой подход доведен до расчетных соотношений применительно к задаче об устойчивости слоя над круговой в плане полостью.

Будем приближенно рассматривать слой связного грунта толщиной m = h_c над круговой полостью радиуса R как круглую пластинку (0 < r < R), защемленную по контуру и загруженную сверху равномерной нагрузкой:

σ_z(R) = σ_l(R) + γ_cm, (16)

где σ_l(R) = max(σ_lB(R), σ_lP(R)). Согласно [16], максимальное значение вызываемого действием нагрузки σ_z(R) растягивающего напряжения на верхней поверхности «пластики» σ^–_ru реализуется на ее внешнем контуре r = R, а соответствующее максимальное значение на нижней поверхности σ^–_rl (R) – на оси (r = 0). Величины σ^–_ru (R) и σ^–_rl (R) оцениваются по формулам [16],

σ^–_ru (R) =  σ^–_rl (R) = 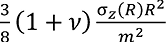. (17)

Значения горизонтального сжимающего напряжения, действующего на контуре пластинки со стороны массива, составляют соответственно на уровне верхней и нижней поверхности:

σ⁺_ru (R) = [γ_d ℎ_d + p₀k_gα(ℎ_d)]μ_c, σ⁺_rl (R) = [γ_d ℎ_d + γ_c ℎ_c + p₀k_gα(H)]μ_c , (18)

а суммарные значения напряжений в указанных выше зонах составляют

σ^Σ_ru = σ⁺_ru (R) – σ_z(R) σ^Σ_rl = σ⁺_rl (R) – (1 + v)σ_z(R) . (19).

Будем считать, что при появлении растягивающих напряжений в слое связного грунта произойдет его разрушение и обрушение в полость с последующим частичным ее заполнением фрагментированной грунтовой массой, а при наличии остаточного свободного аккумуляционного объема – суффозионное перемещение в полость соответствующего объема несвязного грунта. Поэтому значение R, при котором одна из величин (σ^Σ_rl , σ^Σ_ru ) окажется отрицательной, следует считать «критическим» R^b_кр. В рассматриваемом примере тангенциальное напряжение становится растягивающим (отрицательным) на верхней поверхности слоя-плиты при R > R^bU_кр = 5,3 м, а на нижней – при R > R^bL_кр = 6,4 м. Тогда R^b_кр = min(R^bU_кр , R^bL_кр) = 5,3 м.

Окончательное значение «критического» радиуса полости определяется как наименьшее из указанных значений

R_кр = min(R^s_кр , R^b_кр) = 5,3 м, (20)

т. е. при образовании на площадке у кровли массива скальных пород полости с размером в плане более D_кр= 2R_кр потенциально произойдет или «провал», или образование «мульды оседания».

Проведенные вычисления содержат ряд хотя и «стандартных», но недостаточно обоснованных «инженерных» упрощений, например схему оценки бокового давления, последовательность задания нагрузки на кровлю несущего слоя, использование формул для определения напряжений в тонкой пластинке. Однако результаты таких вычислений показывают, насколько существенным является учет возможности реализации отличных от схемы проскальзывания цилиндрического объема грунта сценариев влияния образования полости в скальном массиве на деформации вышележащей грунтовой толщи. Приведем на рис. 3 зависимости от мощности h^H_c нижнего несущего слоя, изменяющейся при неизменной суммарной мощности грунтовой толщи H, значений R_кр(h_c),определенных по обычной «схеме Бирнбаумера» [2][4], т. е. R^B_кр (h_c) = R_max(h_c), и значений R^bU_кр (h_c) = R_min(h_c), определенных с учетом напряжений в несущем слое от изгиба при нагрузке, определяемой по «своду Протодьяконова». Видно, что при увеличении отношения h_c/H в пределах ≈ 5…50 % значения R^B_кр(h_c) = R_max(h_c) вырастают всего примерно в 1,13 раза. То есть в рамках этой схемы оценки критического радиуса полости малочувствительны к геологическому строению грунтовой толщи, и указанная выше процедура расчета по осредненным значениям характеристик представляется вполне эффективной.

Другая картина имеет место при выполненном учете того, что непосредственно над полостью расположен слой, который воспринимает часть нагрузки от веса вышележащей толщи и при этом может не только перемещаться поступательно вместе со всем находящимся над полостью объемом грунта, но и оказаться предварительно разрушенным от растягивающих напряжений и затем инициировать перемещения грунта в этой толще с образованием провала или мульды. Такая модель образования провала близка к описанному В. П. Хоменко [18][19] карстово-обвальному механизму. Как понятно из нелинейного характера зависимостей (17) величин растягивающих напряжений на поверхностях несущего слоя от его мощности, зависимость R_кр от h_c оказывается при таком механизме гораздо более значимой: при таком же, как и в случае «однородной» толщи, возрастании h_c значение R_кр увеличивается примерно в 2,5 раза.

Заключение

Предложены и обоснованы корректировки методик определения размера полости у кровли подстилающего грунтовую толщу скального массива, при котором в этой толще может произойти провал или оседание. Указанный критический размер должен определяться не при используемом в существующих «карстологических» руководствах значении коэффициента устойчивости, равном единице, а при принятых в геотехнике значениях. Поясняется, почему при рекомендуемом на «опасных» по фактору образования полостей территориях применения плитных фундаментов влияние поверхностной нагрузки в расчете возможности сдвига выделенного объема грунта следует учитывать только при определении горизонтальных напряжений и сил трения на контуре сдвигаемого объема, и предложено рациональное упрощение учета этого влияния. Показано, что замена многослойной толщи «эквивалентным» слоем эффективна лишь при обоснованном применении схемы сдвига объема грунта. В рамках приближенных инженерных схем выполнен учет возможности разрушения находящегося непосредственно над полостью нижнего слоя связного грунта при появлении растягивающих напряжений под действием деформаций изгиба. Уточненные с учетом указанных факторов оценки критического размера полости существенно зависят от мощности несущего слоя и меньше значений, получаемых по рекомендуемым в настоящее время методикам. Это означает, что провал или процесс оседания может образоваться раньше, чем прогнозируется по этим методикам, т. е. до окончания расчетного срока эксплуатации сооружения.