Перейти к:
Экспериментальные исследования процесса релаксации бетона в разных режимах
https://doi.org/10.37538/2224-9494-2023-1(36)-86-98
Аннотация
Введение. В настоящее время при проведении длительных испытаний бетонных образцов под нагрузкой основным определяемым параметром является ползучесть бетона. При этом ползучесть является только одним из деформационных свойств бетонного образца при работе под действием длительной нагрузки. Другим важным свойством является релаксация напряжений, причем в отдельных задачах (температурные задачи, задачи, связанные с перераспределением усилий, и т. д.) релаксация играет более важную роль, чем ползучесть. Внедрение новой методики испытаний позволит повысить точность полученных результатов (при стандартных испытаниях на ползучесть релаксация бетона определяется только математически), что, в свою очередь, даст возможность повысить точность расчетов.
Цель. Разработка методики проведения испытаний образцов бетона с определением в них релаксации напряжений.
Материалы и методы. В статье описывается методология постановки эксперимента по исследованию релаксации бетонных образцов в режиме «сжатие» и в режиме «изгиб», описываются параметры испытательных установок, испытываемых образцов и принципы передачи нагрузки.
Результаты. В статье в графическом виде приведены основные результаты проведенных экспериментальных исследований. Выполнен их анализ, а также произведена оценка удобства проведения таких испытаний.
Выводы. Показана перспективность предложенного подхода к испытанию бетонных образцов, подготовлены рекомендации по внесению изменений в ГОСТ 24544.
Для цитирования:
Арленинов П.Д., Крылов С.Б., Калмакова П.С., Донов А.В. Экспериментальные исследования процесса релаксации бетона в разных режимах. Вестник НИЦ «Строительство». 2023;36(1):86-98. https://doi.org/10.37538/2224-9494-2023-1(36)-86-98
For citation:
Arleninov P.D., Krylov S.B., Kalmakova P.S., Donov A.V. Experimental studies of concrete relaxation in various modes. Bulletin of Science and Research Center of Construction. 2023;36(1):86-98. (In Russ.) https://doi.org/10.37538/2224-9494-2023-1(36)-86-98
Введение
В настоящее время как в нашей стране, так и за рубежом при проведении длительных испытаний под нагрузкой основным параметром, который определяется по результатам этих испытаний, является ползучесть бетона. Это регламентирует как отечественный ГОСТ [1], так и зарубежные стандарты [2–4].
При этом ползучесть бетона является только одним из деформационных свойств бетонного образца при работе под действием длительной нагрузки. Другим важным свойством является релаксация напряжений.
Испытания бетонных образцов на ползучесть имеют два серьезных недостатка. Первый – необходимость постоянно проверять, что в испытательной установке поддерживается неизменная сжимающая сила. А поскольку это условие нарушается, то необходимо все время корректировать величину сжимающего усилия. Второй недостаток – испытательная установка достаточно сложна. В результате такие испытания могут проводить всего лишь несколько организаций в нашей стране. Для испытаний на релаксацию потребуются более простые установки, в которых поддерживаются заданные деформации образцов, измеряются усилия в образцах. Постоянный контроль и обслуживание таких установок во время испытаний не требуются. Это позволяет повысить точность результатов и существенно упростить испытания, сделать их более доступными.
В температурных задачах и задачах, связанных с перераспределением усилий, релаксация играет более важную роль, чем ползучесть. При выполнении таких расчетов сначала определяется мера ползучести бетона, затем через меру ползучести определяется ядро ползучести, а через ядро ползучести определяется ядро релаксации, через которое уже определяются прогнозируемые напряжения в бетоне в произвольный момент времени.
Внедрение новой методики испытаний позволит повысить точность полученных результатов, что, в свою очередь, даст возможность повысить точность расчетов, при этом с достаточной надежностью приведет к удешевлению конструкции. Упрощение способа испытаний позволит выполнять их более широко. В свою очередь, это позволит получать объективные данные о свойствах бетонов в широком диапазоне составов и прочностей. В связи с этим рассматриваемая тема является актуальной и нужной для развития современной строительной отрасли.
Подобные исследования не проводились ни в нашей стране, ни за рубежом. Поэтому методика проведения предложенных испытаний и результаты этих испытаний являются новыми.
Материалы и методы
Математическое описание процесса релаксации бетона
Явление релаксации тесно связано с явлениями ползучести и усадки бетона, поэтому для понимания природы релаксации необходимо также детально исследовать процессы усадки и ползучести. Математические зависимости, описывающие процессы ползучести и релаксации, также между собой тесно связаны.
Мера ползучести бетона при сжатии Cb применяется для определения деформации ползучести в зависимости от напряжения в бетоне:
ε𝑝𝑙=𝐶𝑏×σ𝑏 ,(1)
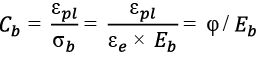 , (2)
, (2)
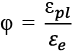 . (3)
. (3)
Мера ползучести бетона зависит от его класса, уровня напряжений и является переменной во времени. Если рассматривать сжатый или растянутый стержень, выполненный из материала, обладающего упругими свойствами, ползучестью, а также старением, и считать, что деформации ɛ*(t) известны, то приведенные ниже зависимости можно трактовать как уравнения относительно неизвестных σ*(τ), σ*(t), E(t).
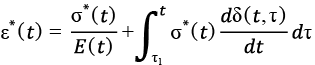 , (4)
, (4)
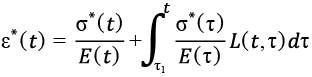 , (5)
, (5)
где t – возраст бетона, сут;
τ – начальный возраст бетона (возраст загрузки), сут;
σ*(τ) – нормальные напряжения, вызванные мгновенными вынужденными относительными деформациями.
В стержне, жестко заделанном по концам, относительные деформации в задаче релаксации остаются постоянными, то есть:
ɛ*(t) = ɛo. (6)
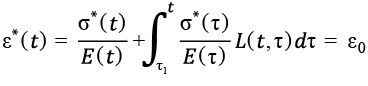 . (7)
. (7)
Из теории ползучести известно, что ядро ползучести имеет вид
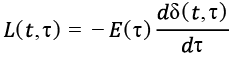 .
.
Учитывая, что напряжения будут определяться постоянными относительными деформациями и текущим модулем упругости, после ряда преобразований выражение для напряжения также приобретает вид:
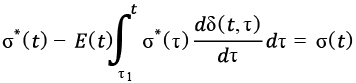 . (8)
. (8)
При постоянных вынужденных деформациях ɛ0(t) = ɛo = const и неравенстве E(t) > E(τ) следует, что при t > τ1
σ(t) < σ(τ1). (9)
Уменьшение во времени напряжений, возникающих при неизменных деформациях образца или конструкции, принято называть релаксацией. При этом процесс релаксации напряжений протекает как при постоянных, так и при переменных деформациях.
С механической точки зрения процесс релаксации напряжений можно объяснить таким образом. При введении постоянных вынужденных деформаций возникают напряжения σ(τ1) пропорциональные соответствующим упруго мгновенным деформациям. В условиях сохранения значений полных деформаций развитие ползучести приводит к уменьшению упруго мгновенных деформаций и, естественно, напряжений. Если стержень выполнен из материала, обладающего ползучестью и старением, то величина релаксации напряжений зависит как от деформаций, так и от продолжительности процесса нагружения.
Обозначим p(t,τ) напряжение, необходимое для поддержания в призматическом образце в любой момент t единичной относительной деформации при загружении образца в момент времени τ. Тогда в начальный момент времени t = τ
p(t,τ) = E(τ) (10)
Характер семейства кривых p(t,τ) показан на рис. 1.
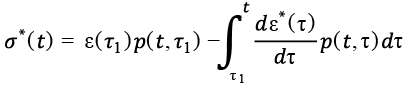 . (11)
. (11)
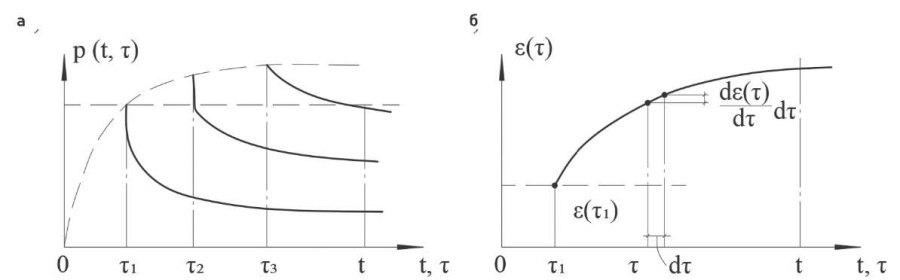
Рис. 1. Графики функции p(t,τ) (а) и относительных деформаций ɛ(t) (б)
Fig. 1. Plots of the p(t,τ) function (а) and relative deformations ɛ(t) (б)
Преобразования позволяют представить уравнение в форме:
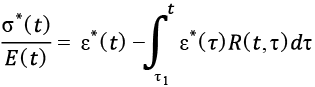 . (12)
. (12)
Причем функция R(t,τ), являющаяся ядром релаксации, определяется по формуле:
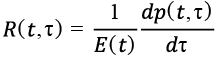 . (13)
. (13)
Эта функция является резольвентой уравнения ползучести.
Таким образом, в линейной теории ползучести существуют две формы зависимости между напряжениями и деформациями:
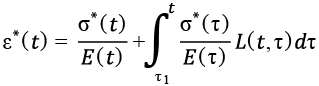 (14)
(14)
или
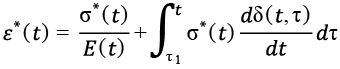 (15)
(15)
и
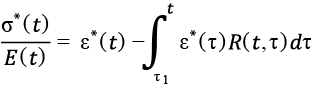 , (16)
, (16)
где δ(t,τ) – полная относительная деформация. Функция δ(t,τ) строится по данным опытов, выполняемых при постоянных напряжениях, а [p(t,τ)] – при постоянных относительных деформациях. Экспериментальные данные для ядра ползучести получают значительно чаще, чем для ядра релаксации. Такие эксперименты практически не ставятся. Приведенная ниже методика экспериментального определения параметров релаксации как раз нацелена на получение данных параметров.
Постановка эксперимента
В рамках данного исследования был проведен комплекс длительных испытаний. Исследования проводились на экспериментальной площадке АО «ВНИИГ им. Б. Е. Веденеева». Одновременно были задействованы следующие испытательные установки, часть из них уникальна и специально разработана и изготовлена под данное исследование:
- установки для определения ползучести бетонных призм при сжатии. Это стандартные пружинные установки, на которых выполняются такие испытания;
- установки для определения релаксации бетонных призм при сжатии. Такие установки были подготовлены путем разбора пружинных установок для испытаний на ползучесть с удалением в них пружин для фиксации требуемых начальных деформаций (рис. 2–3);
- совмещенные установки для определения релаксации или ползучести при изгибе. Такие установки были подготовлены путем модернизации существующих установок стеллажного типа для проведения испытаний на ползучесть при изгибе. Модернизированная установка позволяет на нижнем ярусе проводить испытания образцов балок на ползучесть при изгибе с загрузкой постоянной гравитационной нагрузкой (в качестве нагружающего устройства используются емкости с дробью) и испытания образцов балок на релаксацию бетона на верхнем ярусе с загрузкой их постоянной деформацией. Фотография фрагмента установки для проведения испытаний по определению релаксации приведена на рис. 4, схема испытания приведена на рис.

Рис. 2. Общий вид установки с образцами-призмами при проведении испытаний для определения релаксации напряжений при сжатии
Fig. 2. General view of the test bench with prismatic samples during the compressive stress relaxation tests
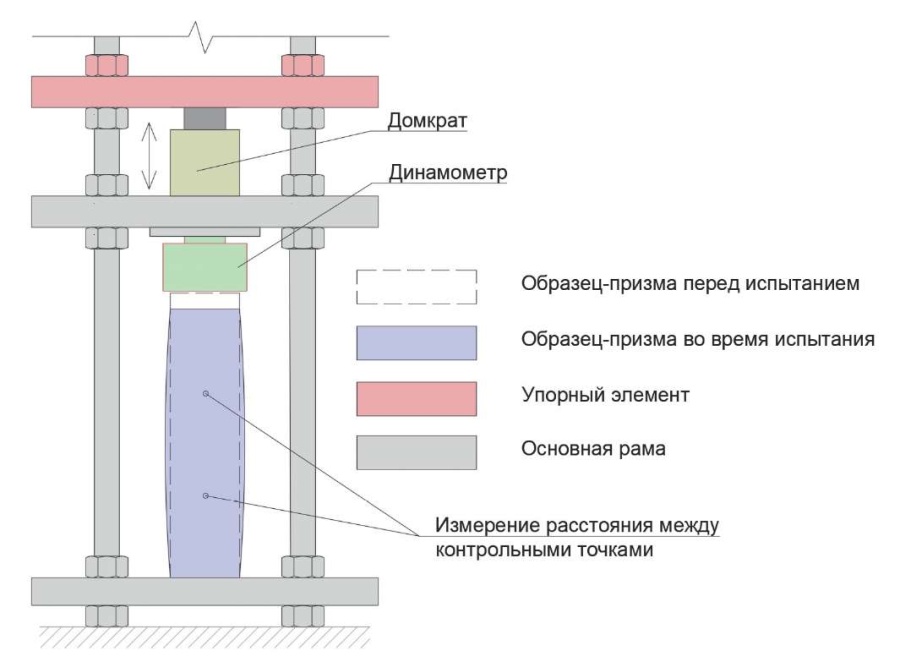
Рис. 3. Схема испытания для определения релаксации напряжений при сжатии
Fig. 3. Test scheme for the determination of compressive stress relaxation

Рис. 4. Установленный образец балки для проведения длительных испытаний по определению релаксации напряжений в бетоне при изгибе
Fig. 4. Installed beam sample for the long-term tests of concrete for bending stress relaxation
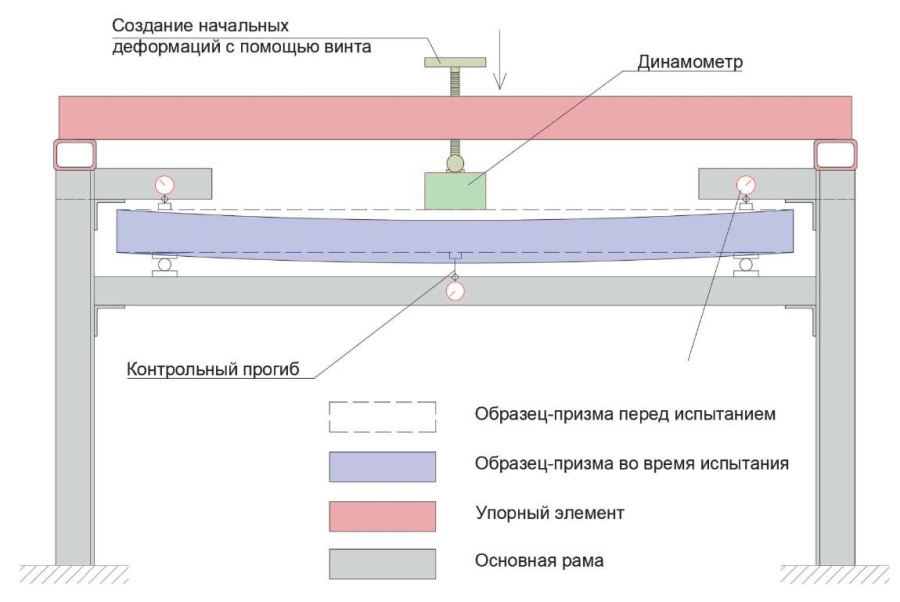
Рис. 5. Схема испытания для определения релаксации напряжений при изгибе
Fig. 5. Test scheme for the determination of bending stress relaxation
Дополнительно были изготовлены установки по определению релаксации в режиме «изгиб» с помощью обратного нагружения. Суть метода в том, что образец в установке находится в перевернутом состоянии для минимизации деформаций ползучести и нагружение начальной деформацией происходит снизу вверх.
Испытания проводились в климатических камерах с поддержанием стабильной температуры и влажности в соответствии с ГОСТ 24544 [1].
Бетонные образцы изготавливались двух классов по прочности на сжатие (В30 и В60), испытания проводились начиная с возраста 28 суток. Параллельно проводились испытания по определению релаксации напряжений в бетоне и на ползучесть при сжатии и изгибе для последующей математической обработки результатов.
Результаты исследования
Ниже в графическом виде приведены результаты эксперимента по определению указанных деформационных характеристик бетонных образцов (ползучесть и релаксация) как в режиме «сжатие», так и в режиме «изгиб» (рис. 6–7).
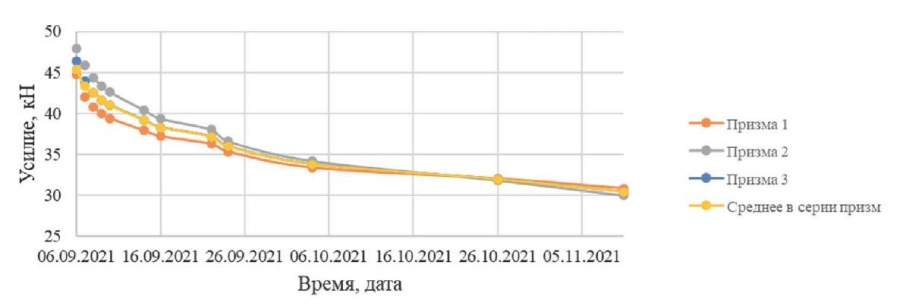
Рис. 6. Графики изменения напряжений в серии образцов призм по определению релаксации при сжатии (бетон В30)
Fig. 6. Plots of stress variations in a series of prismatic samples for the determination of compressive relaxation (B30 concrete)
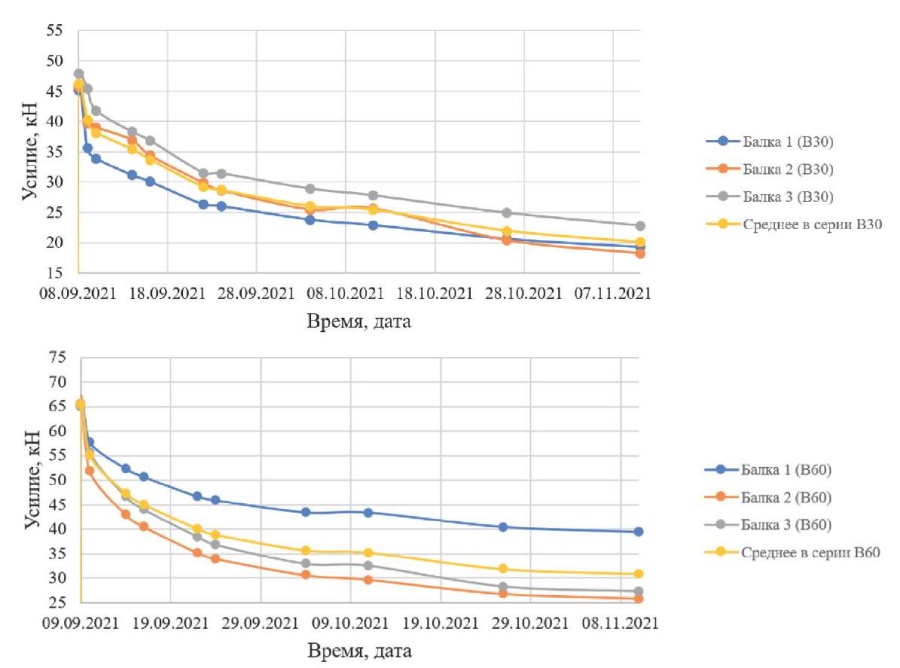
Рис. 7. Графики изменения усилий в серии образцов-балок по определению релаксации напряжений при изгибе (бетон В30 и В60)
Fig. 7. Plots of stress variations in a series of beam samples for the determination of bending stress relaxation (B30 and B60 concrete)
Выводы
Результатами эксперимента являются графики зависимости деформаций во времени (ползучесть бетонных образцов) при постоянной нагрузке, а также графики усилие–время (релаксация) при фиксированных деформациях. Полученные результаты при испытаниях на релаксацию в образцах-балках свидетельствуют об успешности примененной методики – происходит падение напряжений в балке при фиксированных деформациях.
Как видно из рис. 6, падение напряжений в образцах-призмах (релаксация напряжений в призмах) за 200 часов составило от 18 до 20 %, при этом установленное измерительное оборудование не зафиксировало деформации данных призм, что говорит об успешной реализации предлагаемой методики.
На рис. 7 представлены графики зависимости изменения усилия в образце во времени для образцов-балок из бетона класса В30. После нагружения произошло падение напряжений на 25–30 % от первоначальных. Для образцов-балок из бетона класса В60 после нагружения произошло падение напряжений на 22–38 % от первоначальных.
Помимо получения прямых результатов эксперимента в ходе его подготовки и проведения было выявлено, что при проведении испытаний балок предпочтительно использовать одну цилиндрическую катковую опору, а другую – шаровую (справедливо как для испытаний на ползучесть, так и на изгиб). Это уменьшит влияние неплоскостности нижней поверхности испытываемой балки. В случае двух цилиндрических катковых опор возможно неплотное примыкание балки к опоре и, как следствие, вертикальное перемещение центральной оси балки на опорах. При закручивании балки перемещения при изгибе могут быть с обратным знаком. Данный вывод одновременно распространяется и на испытания на ползучесть бетонных образцов при изгибе, и на релаксацию. Подготовлены предложения по внесению изменений в ГОСТ 24544.
Предложенная методика испытаний бетонных образцов на изгиб будет предназначена в первую очередь для специализированных лабораторий, проводящих стандартные длительные испытания, также она позволит удешевить сам процесс испытаний и наравне с внедренной в ГОСТ 24544-2020 методикой испытания на ползучесть бетонных балок расширит количество потребителей, испытательные установки возможно будет установить на крупных строительных площадках непосредственно для конкретного объекта (например, в атомной и энергетической отрасли).
Численный анализ экспериментальных исследований и аналитическое сравнение полученных результатов при испытаниях в разных режимах будут приведены в рамках отдельной статьи.
Список литературы
1. ГОСТ 24544-2020. Бетоны. Методы определения деформаций усадки и ползучести [интернет]. Режим доступа: https://docs.cntd.ru/document/1200177303 (дата доступа 20.09.2021).
2. ASTM C512. Standard Test Method for Creep of Concrete in Compression. Publication Date: 31 Dec. 2010. https://doi.org/10.1520/c0512-02
3. European Committee for Standardization (CEN). EN 12390-17:2019. Testing hardened concrete – Part 17: Determination of creep of concrete in compression. Publication Date: 1 October 2019.
4. International Organization of Standards. ISO 1920-9 Testing of concrete — Part 9: Determination of creep of concrete cylinders in compression. Publication Date: 1 April 2009.
5. Загрядский И.И. Алгоритм численного определения деформаций бетона с учетом ползучести на основе его известных напряжений. Уточнение свойств мер релаксации и мер ползучести молодого бетона. Известия ВНИИГ им. Б.Е. Веденеева. 2014;273:96–107.
6. Киорино М.А. Анализ конструктивных воздействий, зависимых от времени свойств бетона: международный согласованный формат (перевод с англ. яз.). Вестник НИЦ «Строительство». 2018;(1):48–66.
7. Гайджуров П.П., Исхакова Э.Р. Модели теории ползучести бетона и их конечноэлементная реализация. Вестник Донского государственного технического университета. 2012;12(7):99–107.
8. Загрядский И.И. Оценка точности приближенных аналитических зависимостей функции релаксации бетона от его функции ползучести. Известия ВНИИГ им. Б.Е. Веденеева. 2014;272:59–69.
9. Крылов С.Б., Гончаров Е.Е. Решение задачи релаксации бетона в дифференциальной форме. Строительство и реконструкция. 2015;(3):26–31.
10. Гурьева Ю.А. Упрощенная теория нелинейной ползучести бетона при сжатии. Вестник гражданских инженеров. 2008;(2):37–41.
11. Charpin L., Sanahuja J. Creep and relaxation Poisson's ratio: Back to the foundations of linear viscoelasticity. Application to concrete. International Journal of Solids and Structures. 2017;110-111:2–14. https://doi.org/10.1016/j.ijsolstr.2017.02.009
12. Shen D., Wena C., Kang J., Shi H., Xu Z. Early-age stress relaxation and cracking potential of High-strength concrete reinforced with Barchip fiber. Construction and Building Materials. 2020;258:119538. https://doi.org/10.1016/j.conbuildmat.2020.119538
13. Beushausen H., Alexander M.G. Failure mechanisms and tensile relaxation of bonded concrete overlays subjected to differential shrinkage. Cement and Concrete research. 2006:36(10):1908–1914. https://doi.org/10.1016/j.cemconres.2006.05.027
14. Тамразян А.Г. К устойчивости внецентренно сжатых железобетонных элементов с малым эксцентриситетом с учетом реологических свойств бетона. Железобетонные конструкции. 2023;2(2):48–57.
Об авторах
П. Д. АрлениновРоссия
Петр Дмитриевич Арленинов, канд. техн. наук, заместитель заведующего лабораторией механики железобетона; доцент кафедры железобетонных
и каменных конструкций
2-я Институтская ул., д. 6, к. 5, г. Москва, 109428, Российская Федерация
Ярославское шоссе, д. 26, г. Москва, 129337, Российская Федерация
тел.: +7 (499) 174-74-07
С. Б. Крылов
Россия
Сергей Борисович Крылов, д-р техн. наук, заведующий лабораторией механики железобетона
2-я Институтская ул., д. 6, к. 5, г. Москва, 109428, Российская Федерация
тел: +7 (965) 322-21-47
П. С. Калмакова
Россия
Полина Сергеевна Калмакова, инженер лаборатории механики железобетона
2-я Институтская ул., д. 6, к. 5, г. Москва, 109428, Российская Федерация
тел: +7 (916) 239-38-95
А. В. Донов
Россия
Алексей Валентинович Донов, заведующий лабораторией экспертизы, строительного контроля, сопровождения бетонных и ремонтных работ
ул. Гжатская, д. 21, Санкт-Петербург, 195220, Российская Федерация
тел: +7 (921) 633-79-83
Рецензия
Для цитирования:
Арленинов П.Д., Крылов С.Б., Калмакова П.С., Донов А.В. Экспериментальные исследования процесса релаксации бетона в разных режимах. Вестник НИЦ «Строительство». 2023;36(1):86-98. https://doi.org/10.37538/2224-9494-2023-1(36)-86-98
For citation:
Arleninov P.D., Krylov S.B., Kalmakova P.S., Donov A.V. Experimental studies of concrete relaxation in various modes. Bulletin of Science and Research Center of Construction. 2023;36(1):86-98. (In Russ.) https://doi.org/10.37538/2224-9494-2023-1(36)-86-98


























