Перейти к:
Модель комплекса SCAD из объемных конечных элементов: расчет железобетонных кессонных перекрытий
https://doi.org/10.37538/2224-9494-2023-2(37)-18-36
EDN: DPLFAF
Аннотация
Введение. Современные требования на проектирование зданий обязывают проектировщиков применять конструкции, способные сопротивляться прогрессирующему обрушению. К таким конструкциям относится часторебристое железобетонное перекрытие кессонного типа. Пространственные системы являются многократно статически неопределимыми, их расчет осуществляется в программных комплексах, основанных на методе конечных элементов. Модели ребристых конструкций можно создать из различных типов конечных элементов. Усилия, определенные при помощи разных моделей, могут значительно отличаться. Это подтверждается примерами, имеющимися в литературе.
Целью работы является обнаружение простой и точной конечно-элементной модели для расчета на компьютере ребристого железобетонного кессонного перекрытия.
Материалы и методы. Методика выполнения работы предусматривает сравнение изгибающих моментов, полученных аналитическим способом, с данными метода конечных элементов вычислительного комплекса SCAD в балках кессонного перекрытия размером в плане 12,0 × 18,0 м с кессонами 1,5 × 2,25 м. Выполнен расчет стержневой модели, состоящей из системы перекрестных балок таврового сечения и твердотельной модели из объемных конечных элементов.
Результаты. Значения изгибающих моментов, вычисленные аналитическим способом и при помощи твердотельной модели, имеют близкие значения. Максимальные отклонения компьютерного расчета от аналитического способа составляют от -3,2 до +2,6 %. Максимальные отклонения значений изгибающих моментов, полученных при сравнении твердотельной модели со стержневой, составляют от -9,2 до +4,0 %.
Выводы. Конечно-элементная модель, расчет которой основан на решении объемной задачи теории упругости, является эффективной верификационной моделью изучения сложных систем, но трудоемкой при ее создании и непростой при анализе полученных данных. Твердотельную модель можно рекомендовать для изучения отдельных конструкций или их критических зон.
Ключевые слова
Для цитирования:
Мозголов М.В., Козлова Е.В. Модель комплекса SCAD из объемных конечных элементов: расчет железобетонных кессонных перекрытий. Вестник НИЦ «Строительство». 2023;37(2):18-36. https://doi.org/10.37538/2224-9494-2023-2(37)-18-36. EDN: DPLFAF
For citation:
Mozgolov M.V., Kozlova E.V. SCAD model of solid finite elements: calculation of reinforced concrete waffle slabs. Bulletin of Science and Research Center of Construction. 2023;37(2):18-36. (In Russ.) https://doi.org/10.37538/2224-9494-2023-2(37)-18-36. EDN: DPLFAF
Введение
Ребристые железобетонные конструкции перекрытий находят широкое применение в современном монолитном строительстве. Плиты, усиленные снизу монолитно связанными с ними балками, по сравнению с безбалочными конструкциями позволяют перекрывать большие пролеты, при наличии главных балок позволяют образовывать рамы несущего каркаса здания, придавать ему большую жесткость и устойчивость. Эффективной пространственно работающей конструкцией является часторебристое перекрытие кессонного типа. В качестве примера такой конструкции в Москве можно отметить павильон № 29 ВДНХ «Цветоводство и озеленение», построенный в 1969–1971 гг. В настоящее время в нашей стране при строительстве ребристых перекрытий получают распространение опалубочные системы Skydome, Holedeck, Победа и другие.
В связи с принятием норм СП 385.1325800.2018 «Защита зданий и сооружений от прогрессирующего обрушения. Правила проектирования. Основные положения» на проектирование зданий и сооружений нормального и повышенного уровней ответственности в целях их защиты от прогрессирующего обрушения пространственно работающие конструкции будут получать распространение [1]. Пространственные системы с точки зрения строительной механики являются многократно статически неопределимыми, и их расчет без использования современных компьютерных программ, основанных на методе конечных элементов (МКЭ), затруднителен или невозможен. Кроме этого, в соответствии с современными требованиями градостроительного законодательства (Градостроительный кодекс РФ от 29.12.2004 № 190-ФЗ [2], СП 333.1325800.2020 «Информационное моделирование в строительстве. Правила формирования информационной модели объектов на разных стадиях жизненного цикла» [3]) прочностной расчет строительных конструкций объектов, подлежащих экспертизе, в скором времени должен будет выполняться по BIM технологии путем создания цифровой информационной модели здания. В соответствии с ч. 12 ГОСТ 27751-2014 «Надежность строительных конструкций и оснований. Основные положения» при проектировании объектов должен проводиться контроль качества проектной продукции, минимальные требования которого включают в себя проверку адекватности расчетных моделей, их точность, проведение параллельных расчетов с использованием независимо разработанных сертифицированных программных средств и другие требования [4]. Расчет на электронно-вычислительной машине (ЭВМ) осуществляется в программных комплексах, реализующих метод конечных элементов, при котором вычисленные в элементах усилия или напряжения могут оказаться недостоверными, и причин этому достаточно. Так, например, создав сетку конечных элементов (КЭ) неверной густоты, расчетчик получит результат, значительно отличающийся от правильного [5–10].
Современные программные комплексы включают в себя широкий набор различных типов конечных элементов, из которых можно создать ребристую конечно-элементную модель (КЭМ). Авторами работ [7][8] указывается, что «При составлении компьютерной модели комбинированных систем (плита, подпертая ребрами; плоские или пространственные рамно-связевые системы; плита, опирающаяся на вертикальные стержни и др.) могут возникнуть различные трудности». По состоянию на 2022 г. в работе [11] отмечается, что на современном этапе развития компьютерных расчетов при моделировании ребристых конструкций «До сих пор не предложена оптимальная расчетная схема, с одной стороны, обладающая достаточной простотой для проведения инженерного анализа, а с другой стороны, позволяющая с большой точностью отражать особенность работы элементов перекрытия». Имеющиеся в литературе данные расчета ребристых железобетонных конструкций показывают, что в зависимости от созданной конечно-элементной модели усилия в балках могут существенно отличаться [11–14]. Например, при расчете железобетонных кессонных перекрытий в моделях, в которых полка плиты задается оболочечными конечными элементами, а ребра стержневыми элементами, отнесенными от полки жесткой вставкой, максимальные отклонения усилий в балках, полученных методом конечных элементов от аналитического расчета, составляют: 50 [12], 40 [13], 22,1 % [14].
В работе [11] сравниваются продольные относительные деформации по высоте поперечного сечения балок, значения которых получены при помощи четырех конечно-элементных моделей расчета ребристой шарнирно опертой по контуру плиты 6,0 × 12,0 м. Первая модель представляет собой конструкцию, состоящую из стержневых конечных элементов – балок таврового сечения. Вторая модель состоит из оболочек, моделирующих плиту, и стержней, выполняющих функцию ребер. Соединение элементов выполнено абсолютно жесткими телами. В третьей модели как плита, так и ребра представлены оболочками, соединенными абсолютно жесткими телами. Четвертая модель выполнена в виде массивного тела, состоящего из объемных конечных элементов. В соответствии с выводом проведенного численного эксперимента наименьшие деформации получены в четвертой модели, состоящей из объемных конечных элементов и принятой автором за эталон. Наиболее близкой к четвертой модели оказалась самая простая первая модель, состоящая из стержней. Отклонения деформаций в растянутой зоне составляют +3,9 %, в сжатой +9,2 %. Наибольшие отклонения от четвертой модели показала вторая модель, в растянутой зоне расхождения составляют +72 %, в сжатой +75,3 %. Отклонения третьей модели в растянутой зоне +44,5 %, в сжатой +42,7 %.
Для обоснования надежности расчетов, созданных моделей метода конечных элементов, в п. 6 ГОСТ Р 57700.10-2018 «Численное моделирование физических процессов. Определение напряженно-деформированного состояния. Верификация и валидация численных моделей сложных элементов конструкций в упругой области» [15] перечислены требования к порядку верификации и валидации расчетной модели для численного моделирования в упругой области напряженно-деформированного состояния (НДС) сложных элементов конструкций. Одним из методов контроля полученных данных по МКЭ является расчет конструкции при помощи разных моделей.
Данная работа является продолжением изучения аналитического метода расчета прямых кессонных железобетонных перекрытий и их моделирования в вычислительном комплексе SCAD [16][17]. Ранее рассматривались стержневые конечно-элементные модели, которые обладают как достоинствами, так и недостатками [14][17]. Известный аналитический метод расчета кессонных перекрытий уточнен, в формулы определения составляющих общей нагрузки, приходящиеся на ортогональные балки, введены жесткости. Стержневые конечно-элементные модели показали хорошую сходимость с уточненным аналитическим методом расчета, однако есть предположение, что данные модели не в полной мере учитывают пространственную работу кессонной конструкции. В работах [11][18][19] при расчете железобетонных конструкций рассматриваются пространственные конечно-элементные модели, состоящие из объемных, плоских и линейных элементов. Отмечается, что при помощи моделей, решение которых основано на объемной задаче теории упругости, получается близкая к действительности картина НДС. В работе [21] при анализе причин обрушения конструкций покрытия СОК «Трансвааль-парк» отмечается, что критические зоны стыковки ребер и скорлупы необходимо изучать на объемных бетонных элементах, а тестовые расчеты показали адекватность объемной модели даже при одном слое элементов по толщине. В то же время объемные модели характеризуются высокой трудоемкостью их создания, большой размерностью задачи и сложностью анализа полученного результата [6][11][18][19].
Методика выполнения работы предусматривает сравнение усилий – изгибающих моментов, полученных уточненным аналитическим способом, с учетом пролетов, жесткости конструкции и методом конечных элементов в вычислительном комплексе SCAD во всех пролетных балках кессонного перекрытия размером в плане 12,0 × 18,0 м с кессонами 1,5 × 2,25 м (по осям).
Цель
Целью работы является поиск простой и наиболее точной конечно-элементной модели для расчета ребристого железобетонного кессонного перекрытия, а также выявление теоретических резервов несущей способности по изгибающему моменту у стержневой модели при сравнении ее с объемной моделью.
Материалы и методы исследования
За основу численного эксперимента принята конструкция кессонного перекрытия размером в плане (Lx × Ly) 12,0 × 18,0 м с кессонами 1,5 × 2,25 м (по осям) (рис. 1) как наиболее сложная для аналитического расчета, данные которой частично представлены в работе [17]. Высота перекрытия составляет 500 мм, толщина полки – 80 мм, ширина ребер балок – 250 мм. Конструкция запроектирована из бетона класса B25.
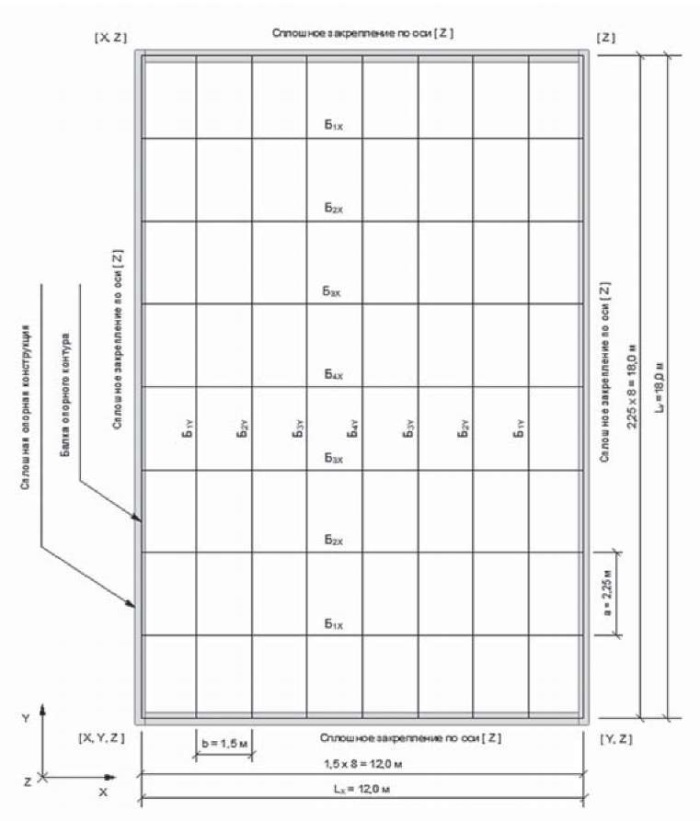
Рис. 1. Схема кессонного перекрытия размером в плане 12,0 × 18,0 м с кессонами 1,5 × 2,25 м.
Б1X, Б2X, Б3X, Б4X, Б1Y, Б2Y, Б3Y, Б4Y – рассчитываемые балки; [X, Y, Z] – связи, установленные в узлах балки опорного контура
Fig. 1. Schematic of a waffle slab of 12.0 x 18.0 m in plan having 1.5 x 2.25 m caissons. Б1X, Б2X, Б3X, Б4X, Б1Y, Б2Y, Б3Y, Б4Y – calculated beams; [X, Y, Z] – connections established in beam nodes of supporting structure
Выполним аналитический расчет в соответствии с теорией, учитывающей пролеты конструкции Lx и Ly, относительную жесткость балок Dx и Dy. Жесткость балок Bx и By определена в вычислительном комплексе SCAD. Рассматриваем пролетные балки Б1X, Б2X, Б3X, Б4X, Б1Y, Б2Y, Б3Y, Б4Y (рис. 1).
В соответствии с требованиями п. 6.2.5 СП. 430.1325800.2018 «Монолитные конструктивные системы. Правила проектирования» [20] и п. 2.1.1.1 Методического пособия [22] для учета ползучести бетона и наличия трещин, как и в работе [17], начальный модуль упругости бетона умножался на коэффициент 0,2 для участков с трещинами (пролетные участки) и 0,3 для участков без трещин (опорный контур размером 0,25 × 0,5(h) м).
Максимальные изгибающие моменты в балках, расположенных вдоль осей X и Y, определяются по формулам:
𝑀𝑥𝑚𝑎𝑥 = α1 × 𝑞𝑥 × 𝑎 × 𝐿2𝑥 × 𝑛𝑥,(1)
𝑀y𝑚𝑎𝑥 = α2 × 𝑞y × b × 𝐿2y × 𝑛y,(2)
где α1 и α2 – коэффициенты, зависящие от характера распределения нагрузки и вида опорных закреплений. При равномерно распределенной нагрузке на перекрытие и шарнирно опертом контуре α1 = α2 = 0,125; a и b – шаг балок; nx и ny – коэффициенты пропорциональности, зависящие от расположения балок в перекрытии.
Составляющие общей нагрузки, приходящиеся на балки qx + qy = q, расположенные вдоль осей X и Y, зависят от размеров пролетов перекрытия Lx и Ly и относительной жесткости Dx и Dy отдельных центральных ортогональных балок, равноотстоящих друг от друга с жесткостью Bx и By.
Bx = E × Ix,(3)
By = E × Iy,(4)
где Е – модуль упругости материала;
Ix и Iy – моменты инерции балок вдоль осей X и Y.
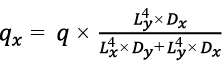 ,(5)
,(5)
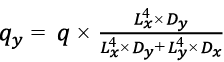 .(6)
.(6)
Относительная жесткость балок с учетом коэффициентов редуцирования:
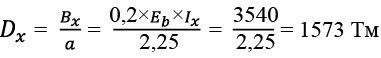 ,(7)
,(7)
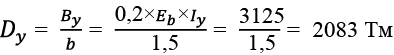 ,(8)
,(8)
где Bx и By – жесткость при изгибе каждой из балок вдоль осей X и Y;
a и b – шаг балок.
Составляющие общей нагрузки, приходящиеся на балки:
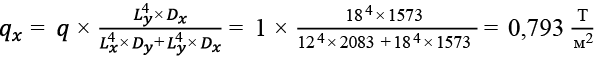 ,(9)
,(9)
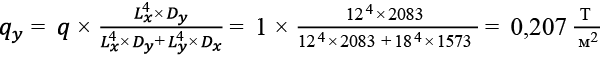 ,(10)
,(10)
Балка Б1Х
Коэффициент пропорциональности, учитывающий расположение балки Б1Х от опорного контура вдоль оси Y.
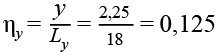 ,(11)
,(11)
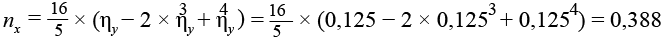 ,(12)
,(12)
Пролетный изгибающий момент
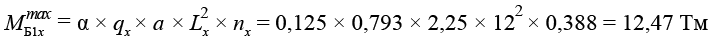 .(13)
.(13)
Балка Б2Х
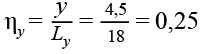 ,(14)
,(14)
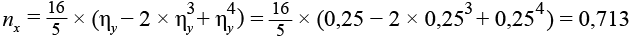 ,(15)
,(15)
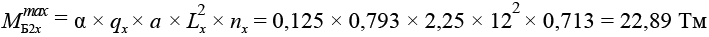 .(16)
.(16)
Балка Б3Х
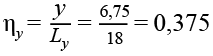 ,(17)
,(17)
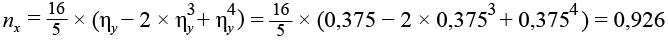 ,(18)
,(18)
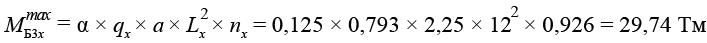 .(19)
.(19)
Балка Б4Х
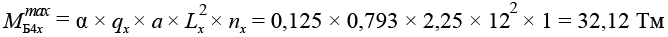 .(20)
.(20)
Балка Б1Y
Коэффициент пропорциональности, учитывающий расположение балки Б1Y от опорного контура вдоль оси X.
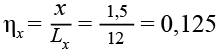 ,(21)
,(21)
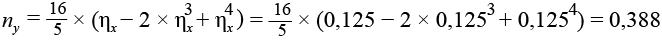 ,(22)
,(22)
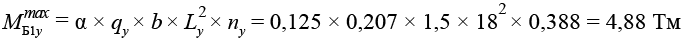 .(23)
.(23)
Балка Б2Y
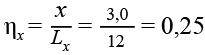 ,(24)*
,(24)*
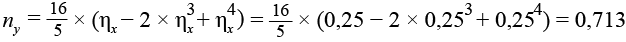 ,(25)
,(25)
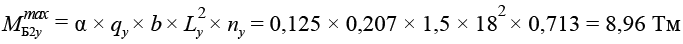 .(26)
.(26)
Балка Б3Y
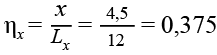 ,(27)
,(27)
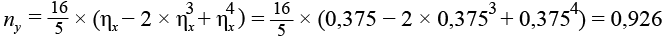 ,(28)
,(28)
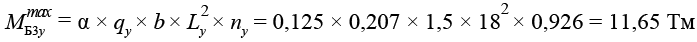 .(29)
.(29)
Балка Б4Y
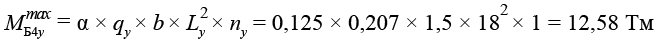 .(30)
.(30)
Результаты аналитического расчета представлены в табл. 2.
Выполним расчет конструкции на ЭВМ в вычислительном комплексе SCAD в линейной постановке задачи как основного исследовательского инструмента строительной механики [23], но с учетом коэффициентов редуцирования начального модуля упругости бетона, учитывающих его ползучесть и трещинообразование [22].
Для создания необходимой густоты сетки конечных элементов твердотельной модели обратим внимание на ряд требований технических норм и рекомендаций специалистов по МКЭ. В соответствии с пп. 5.3.1, 5.3.3 ГОСТ Р 57700.10-2018 «Численное моделирование физических процессов. Определение напряженно-деформированного состояния. Верификация и валидация численных моделей сложных элементов конструкций в упругой области» не допускается при генерации КЭМ с применением твердотельных элементов использовать для тонкостенных конструкций менее трех элементов по толщине, нежелательно использовать тетраэдральные элементы первого порядка при проведении численного моделирования в 3D-постановке [15]. Точность расчета зависит не только от типа конечного элемента, но и от способа расположения конечных элементов и их ориентации по отношению к потокам основных напряжений [5]. При назначении расчетной сетки предпочтение нужно отдавать равносторонним элементам (равносторонний треугольник, квадрат, равносторонний тетраэдр, куб) [6–10]. Если не получается оптимальное разбиение, то для четырехугольных элементов следует ограничить их стремление к «игольчатой форме». Вытянутость четырехугольников рекомендуется ограничить в пределах 0,25–1, а рекомендуемый коэффициент формы должен быть 1–4 [10].
Выполняя данные рекомендации, в «ручном» режиме для объемной модели создана регулярная сетка конечных элементов из пространственного изопараметрического восьмиузлового конечного элемента № 36 с местными осями X1, Y1, Z1, совпадающими с глобальной системой координат X, Y, Z. Полка по высоте разбита на три параллелепипеда размером 41,667(x1) × 41,667(y1) × 26,667(z1) мм. Ребра состоят из элементов размером 41,667(x1) × 41,667(y1) × 42(z1) мм. Равномерно распределенная нагрузка q = 1 Т/м2 прикладывалась двумя способами: на верхнюю полку конструкции и к нижней грани балок. В первом случае сверху полки по объемным элементам уложена «пленка» из оболочечных конечных элементов КЭ № 41 толщиной 1 мм и размером в плане 41,667 × 41,667 мм с физико-механическими характеристиками, соответствующими бетону конструкции. Во втором случае аналогичная «пленка», работающая по биссектрисной схеме излома, прикреплялась к нижней грани балок [24]. При расчете конструкции в протоколе выполнения расчета уведомление о геометрически изменяемой системе отсутствовало. 3D-модель представлена на рис. 2.

Рис. 2. Конечно-элементная модель, вид снизу. Поля напряжений σy
Fig. 2. Finite element model, bottom view. Stress fields σy
Для объемной модели, состоящей только из одного материала, в нашем случае бетона, величины изгибающих моментов MБi,x, MБi,y в балках, расположенных вдоль осей X и Y, определяются следующим образом [19, с. 257].
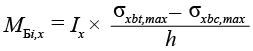 ,(31)
,(31)
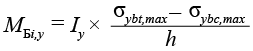 ,(32)
,(32)
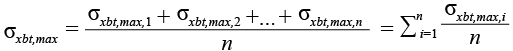 ,(33)
,(33)
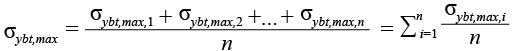 ,(34)
,(34)
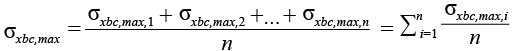 ,(35)
,(35)
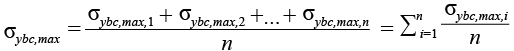 ,(36)
,(36)
где Ix и Iy – моменты инерции балок;
h – высота конструкции;
n – количество анализируемых конечных элементов;
σxbt,max и σybt,max – усредненные максимальные напряжения растяжения в нижней крайней фибре бетона;
σxbc,max, σybc,max – усредненные максимальные напряжения сжатия в верхней крайней фибре бетона.
Важным является выбор анализируемого поперечного сечения балок, так как в местах их пересечения имеет место значительный разброс величин напряжений. Стабильность напряжений можно выявить по изолиниям напряжений (рис. 3). Определив необходимое поперечное сечение, начинаем изучать интересующие нас напряжения с максимальным значением во всех конечных элементах нижней, а затем верхней зон балок (рис. 4–9). В случае приложения нагрузки на верхнюю полку конструкции напряжения в консольных участках тавровых балок увеличиваются. Это связано с суммированием напряжений, возникающих от изгиба балок и изгиба полки, опирающейся на ребра. Анализ НДС полки должен включать в себя комбинации загружений (по всей площади, в четных пролетах, в нечетных пролетах, в шахматном порядке, смежные пролеты и др.). В случае отсутствия в анализируемом месте нагрузки на полку напряжения от ее изгиба по причине многопролетности полки могут оказаться другого знака. Поэтому мы должны учитывать в расчете только напряжения от изгиба балок. Для определения напряжений по сечению тавров без учета изгиба полок применялся второй вариант приложения нагрузки к нижним поверхностям балок (рис. 8, 9). Сравнение полученных данных позволило сделать вывод, что в сжатой зоне над ребрами балок напряжения по первой и второй схемам загружений близки друг другу. При второй схеме загружения в консольных участках тавров напряжения изменяются, к середине пролета конструкции увеличиваются, к опоре уменьшаются, но их среднее арифметическое значение примерно равно напряжениям над ребрами балок. Эти значения мы используем в расчете. Усредненные максимальные величины напряжений в верхних и нижних фибрах бетона балок представлены в табл. 1.
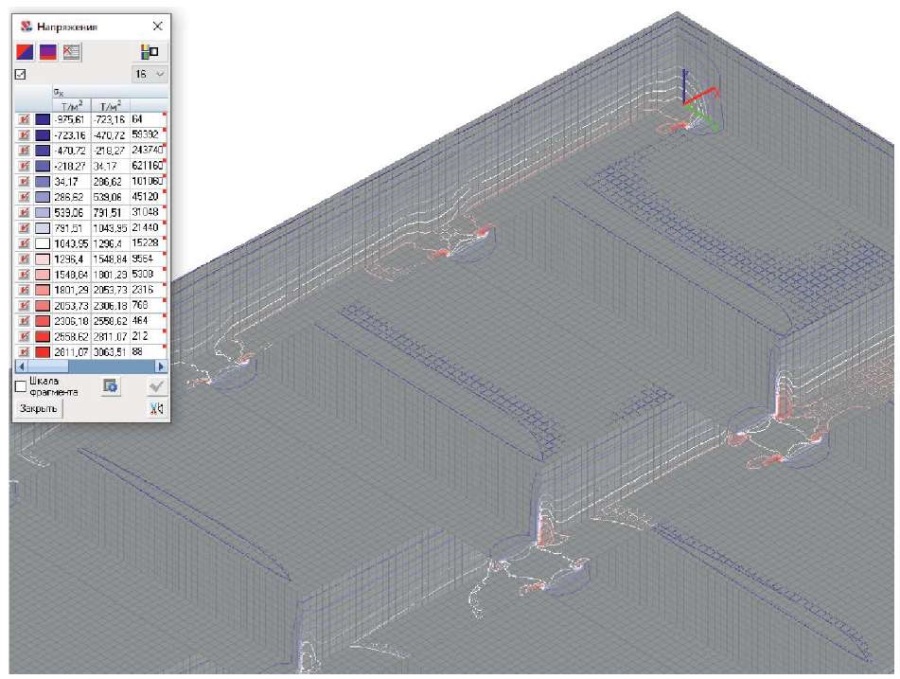
Рис. 3. Фрагмент центральной части перекрытия, вид снизу. Изолинии σx
Fig. 3. Central part of the floor system, bottom view. Contour lines σx
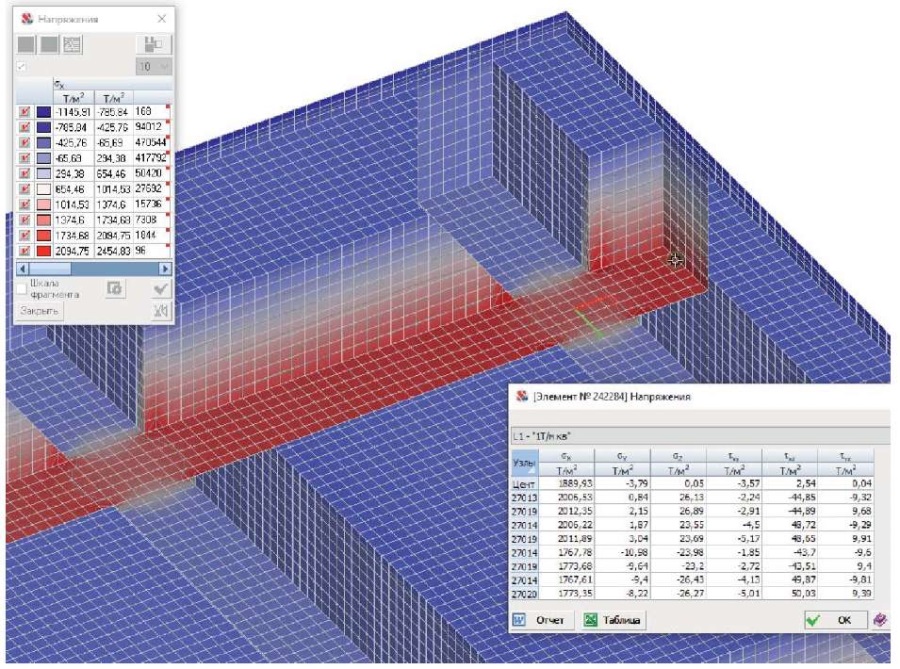
Рис. 4. Фрагмент центральной части перекрытия. Поля напряжений σx. Напряжения в нижней зоне балки Б4x
Fig. 4. Central part of the floor system. Stress fields σx. Stresses in the lower part of the beam Б4x

Рис. 5. Фрагмент центральной части перекрытия. Поля напряжений σx. Напряжения в верхней зоне балки Б4x
Fig. 5. Central part of the floor system. Stress fields σx. Stresses in the upper part of the beam Б4x
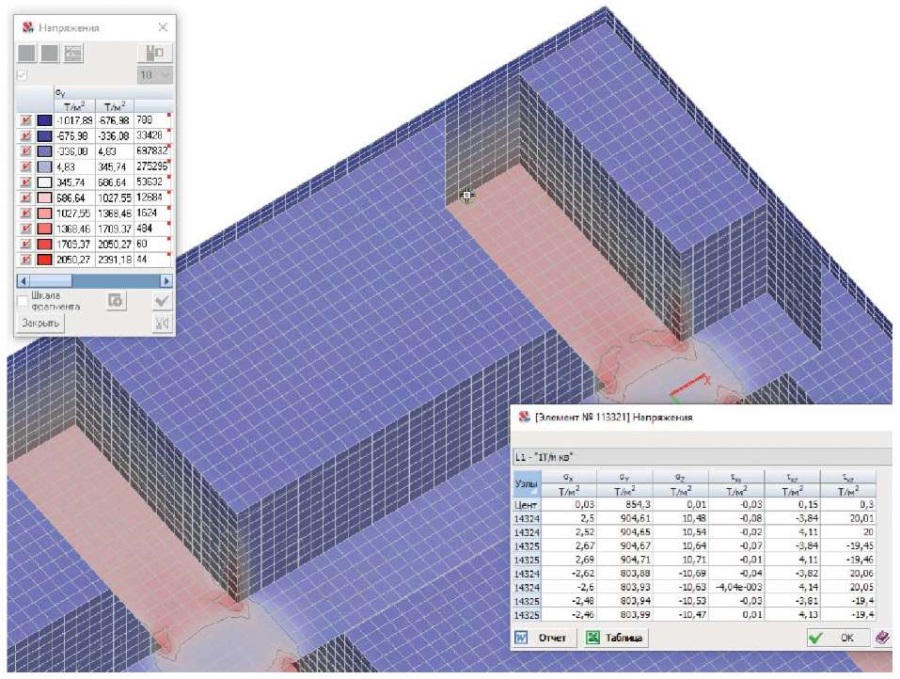
Рис. 6. Фрагмент центральной части перекрытия. Поля напряжений σy. Напряжения в нижней зоне балки Б4y
Fig. 6. Central part of the floor system. Stress fields σy. Stresses in the lower part of the beam Б4y
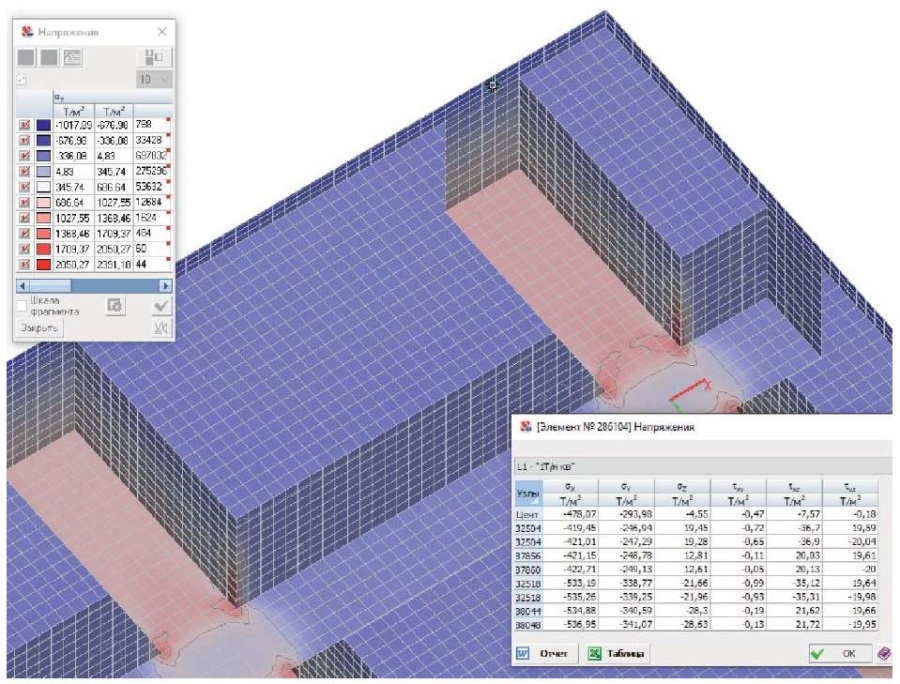
Рис. 7. Фрагмент центральной части перекрытия. Поля напряжений σy. Напряжения в верхней зоне балки Б4y
Fig. 7. Central part of the floor system. Stress fields σy. Stresses in the upper part of the beam Б4y

Рис. 8. Фрагмент центральной части перекрытия. Вторая схема приложения нагрузки. Поля напряжений σx. Напряжения в верхней зоне балки Б4x
Fig. 8. Central part of the floor system. Second load application diagram Stress fields σx. Stresses in the upper part of the beam Б4x

Рис. 9. Фрагмент центральной части перекрытия. Вторая схема приложения нагрузки. Поля напряжений σy. Напряжения в верхней зоне балки Б4y
Fig. 9. Central part of the floor system. Second load application diagram Stress fields σy. Stresses in the upper part of the beam Б4y
Таблица 1
Усредненные максимальные напряжения по верхней и нижней граням балок
Table 1
Average maximum stresses on the upper and lower sides of the beams
Место поперечного сечения балки | Усредненные максимальные напряжения, Т/м2 | |||||||
Балка | ||||||||
Б1X | Б2X | Б3X | Б4X | Б1Y | Б2Y | Б3Y | Б4Y | |
Верхняя зона | -306 | -510 | -645 | -690 | -195 | -270 | -320 | -343 |
Нижняя зона | 800 | 1465 | 1866 | 2000 | 295 | 625 | 835 | 900 |
Определение изгибающих моментов в балках. Моменты инерции Ix и Iy определены в стержневой конечно-элементной модели ВК SCAD работы [17].
Балка, расположенная вдоль оси X: Ix = 578 423,68 см4.
Балка, расположенная вдоль оси Y: Iy = 510 750 см4.
Балка Б1X
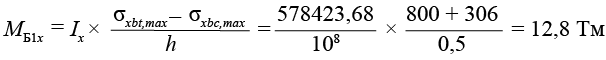 ,(37)
,(37)
Балка Б2X
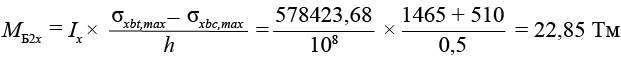 ,(38)
,(38)
Балка Б3X
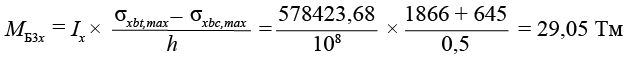 ,(39)
,(39)
Балка Б4X
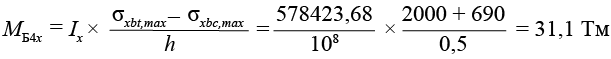 ,(40)
,(40)
Балка Б1Y
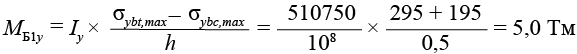 ,(41)
,(41)
Балка Б2Y
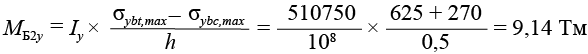 ,(42)
,(42)
Балка Б3Y
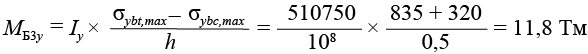 ,(43)
,(43)
Балка Б4Y
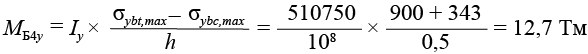 .(44)
.(44)
Прогиб центра перекрытия стержневой конечно-элементной модели составил f = 144 мм,
модели из объемных КЭ f = 125 мм, что можно объяснить влиянием жесткости мест пересечения балок. В стержневой модели это можно учесть, установив в узлы балок жесткие вставки.
Данные аналитического расчета и компьютерных моделей представлены в табл. 2.
Результаты
Таблица 2
Сравнение значений изгибающих моментов в балках кессонного перекрытия (Lx × Ly) 12,0 × 18,0 м с кессонами 1,5 × 2,25 м (в осях), полученные аналитическим методом и при помощи компьютерных моделей вычислительного комплекса SCAD
Table 2
Comparison of bending moment in central beams of a waffle slab of (Lx × Ly) 12.0 x 18.0 m in plan with caissons of 1.5 × 2.25 m (in axes), obtained by analytical method and computer-aided calculations using SCAD software
Метод расчета | Изгибающие моменты, М, Тм | |||||||
Балка | ||||||||
Б1X | Б2X | Б3X | Б4X | Б1Y | Б2Y | Б3Y | Б4Y | |
Аналитический [17] | 12,47 100 % | 22,89 100 % | 29,74 100 % | 32,12 100 % | 4,88 100 % | 8,96 100 % | 11,65 100 % | 12,58 100 % |
SCAD Балочная модель [17] Тавровые балки – пространственный стержень Тип КЭ № 5 | 13,32 106,8 % | 24,58 107,4 % | 31,8 106,9 % | 34,24 106,6 % | 4,88 100 % | 8,79 98,1 % | 11,42 98,0 % | 12,34 98,1 % |
SCAD Объемная модель из пространственного изопараметрического восьмиузлового конечного элемента Тип КЭ № 36 | 12,8 102,6 % | 22,85 99,8 % | 29,05 97,7 % | 31,1 96,8 % | 5,0 102,5 % | 9,14 102 % | 11,8 101,3 % | 12,7 100,9 % |
Выводы
- Значения изгибающих моментов в балках шарнирно опертого по контуру перекрытия прямоугольного в плане с прямоугольными кессонами, вычисленные аналитическим способом с учетом величин пролетов, относительной жесткости балок и методом конечных элементов вычислительного комплекса SCAD при помощи модели решения пространственной задачи теории упругости, состоящей из объемных конечных элементов, имеют близкие значения. Максимальные отклонения метода конечных элементов от аналитического способа расчета составляют от -3,2 до +2,6 %.
- Значения изгибающих моментов в балках шарнирно опертого по контуру перекрытия прямоугольного в плане с прямоугольными кессонами, вычисленные методом конечных элементов вычислительного комплекса SCAD при помощи модели, состоящей из объемных конечных элементов и стержневой модели, имеют близкие значения. Максимальные отклонения объемной модели от стержневой составляют от -9,2 до +4,0 %. Теоретических запасов несущей способности по изгибающему моменту у стержневой конечно-элементной модели не выявлено. Имеющиеся отклонения значений изгибающих моментов двух моделей можно объяснить математическими особенностями расчетов метода конечных элементов.
- Конечно-элементная модель, расчет которой основан на решении объемной задачи теории упругости, является эффективной верификационной моделью изучения сложных систем, но трудоемкой при ее создании и непростой при анализе полученных данных. Модель, состоящую из объемных (бетон) и линейных (арматура) конечных элементов, можно использовать в структурном анализе с учетом наличия фактического армирования конструкции. Однако это можно рекомендовать только для изучения отдельных конструкций или их критических зон.
- В связи с наличием как у стержневой, так и у объемной моделей не только достоинств, но и недостатков дальнейшим исследованием расчета прямых шарнирно-опертых по контуру кессонных железобетонных перекрытий может быть моделирование конструкций на ЭВМ с использованием других типов конечных элементов, например плитных (оболочечных), моделирующих полку, и стержневых, моделирующих ребро, соединенных жесткой вставкой. Сравнивать полученные данные необходимо с уточненным аналитическим методом расчета, учитывающим как пролеты, так и жесткость конструкции.
Список литературы
1. СП 385.1325800.2018. Защита зданий и сооружений от прогрессирующего обрушения. Правила проектирования. Основные положения. Москва: Стандартинформ; 2018.
2. Градостроительный кодекс Российской Федерации: 29 дек. 2004 г., № 190-ФЗ [интернет]. Режим доступа: https://normativ.kontur.ru/document?moduleId=1&documentId=443205
3. СП 333.1325800.2020. Информационное моделирование в строительстве. Правила формирования информационной модели объектов на разных стадиях жизненного цикла [интернет]. Режим доступа: https://docs.cntd.ru/document/573514520
4. ГОСТ 27751-2014. Надежность строительных конструкций и оснований. Основные положения. Москва: Стандартинформ; 2015.
5. Карпиловский В.С., Криксунов Э.З., Маляренко А.А., Фиалко С.Ю., Перельмутер А.В., Перельмутер М.А. SCAD Office. Версия 21. Вычислительный комплекс SCAD ++. Москва: Изд-во «СКАД СОФТ»; 2015.
6. Секулович М. Метод конечных элементов. Москва: Стройиздат; 1993.
7. Городецкий А.С., Евзеров И.Д. Компьютерные модели конструкций. Киев: Факт; 2005.
8. Городецкий А.С., Барабаш М.С., Сидоров В.Н. Компьютерное моделирование в задачах строительной механики. Москва: АСВ; 2016.
9. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. Москва: ДМК Пресс; 2007.
10. Перельмутер А.В. Беседы о строительной механике. Москва: Издательство SCAD Soft, Издательский дом АСВ; 2016.
11. Никитин К.Е., Кирсанов О.А. Сравнительное исследование конечно-элементных методик расчета ребристых железобетонных перекрытий. Строительная механика инженерных конструкций и сооружений. 2022;18(3):242–254. https://doi.org/10.22363/1815-5235-2022-18-3-242-254
12. Малахова А.Н. Монолитные кессонные перекрытия зданий. Вестник МГСУ. 2013;(1):79–86.
13. Шибаева В.Д. Исследование напряженно-деформированного состояния монолитных кессонных перекрытий. Молодой ученый. 2021;(16 часть II):119–123.
14. Мозголов М.В., Козлова Е.В. Верификация моделей SCAD железобетонного кессонного перекрытия на основе аналитического метода расчета, учитывающего пролеты и жесткость конструкции. Вестник БГТУ им. В.Г. Шухова. 2023;8(2):29–40. https://doi.org/10.34031/2071-7318-2022-8-2-29-40
15. ГОСТ Р 57700.10-2018. Численное моделирование физических процессов. Определение напряженно-деформированного состояния. Верификация и валидация численных моделей сложных элементов конструкций в упругой области. Москва: Стандартинформ; 2018.
16. Мозголов М.В., Козлова Е.В. О применении жесткостей аналитического метода расчета прямых железобетонных кессонных перекрытий. Вестник НИЦ «Строительство». 2022;33(2):122–138. https://doi.org/10.37538/2224-9494-2022-2(33)-122-138
17. Мозголов М.В., Козлова Е.В. О применении жесткостей аналитического метода расчета прямых железобетонных кессонных перекрытий. Часть 2. Расчет с относительной жесткостью балок. Вестник НИЦ «Строительство». 2022;35(4):62–79. https://doi.org/10.37538/2224-9494-2022-4(35)-62-79
18. Алямовский А.А. Инженерные расчеты в SolidWorks Simulation. Москва: ДМК Пресс; 2019.
19. Пекин Д.А. Плитная сталежелезобетонная конструкция. Москва: АСВ; 2010.
20. СП 430.1325800.2018. Монолитные конструктивные системы. Правила проектирования. Москва: Стандартинформ; 2019.
21. Белостоцкий А.М., Дубинский С.И. Анализ причин обрушения конструкций покрытия СОК «Трансваальпарк». Ansys Solutions. Русская редакция [интернет]. 2007 Зима: 5–12. Режим доступа: h ttps://scadsoft.com/download/Transvaal.pdf
22. Плоские безбалочные железобетонные перекрытия [интернет]. Москва; 2017. Режим доступа: https://www.faufcc.ru/upload/methodical_materials/mp60_2017.pdf
23. Перельмутер А.В., Тур В.В. Готовы ли мы перейти к нелинейному анализу при проектировании? International Journal for Computational Civil and Structural Engineering. 2017;13(3):86–102. https://doi.org/10.22337/1524-5845-2017-13-3-86-102
24. Мозголов М.В., Козлова Е.В. К вопросу создания верификационной модели для расчета кессонного железобетонного перекрытия в вычислительном комплексе SCAD. Вестник НИЦ «Строительство». 2022;32(1):128–140. https://doi.org/10.37538/2224-9494-2022-1(32)-128-140
Об авторах
М. В. МозголовРоссия
Михаил Валентинович Мозголов, канд. техн. наук, доцент кафедры «Строительное производство»
ул. Октябрьской революции, д. 408, г. Коломна, 140402
Е. В. Козлова
Россия
Елизавета Вадимовна Козлова , студент 4-го года обучения направления «Строительство»
ул. Октябрьской революции, д. 408, г. Коломна, 140402
Рецензия
Для цитирования:
Мозголов М.В., Козлова Е.В. Модель комплекса SCAD из объемных конечных элементов: расчет железобетонных кессонных перекрытий. Вестник НИЦ «Строительство». 2023;37(2):18-36. https://doi.org/10.37538/2224-9494-2023-2(37)-18-36. EDN: DPLFAF
For citation:
Mozgolov M.V., Kozlova E.V. SCAD model of solid finite elements: calculation of reinforced concrete waffle slabs. Bulletin of Science and Research Center of Construction. 2023;37(2):18-36. (In Russ.) https://doi.org/10.37538/2224-9494-2023-2(37)-18-36. EDN: DPLFAF


























