Перейти к:
Оценка возможности применения полевого моделирования пожара для проведения расчетов пожаров в зданиях и помещениях
https://doi.org/10.37538/2224-9494-2023-2(37)-37-70
EDN: ETZDYW
Аннотация
Введение. В данной статье представлена информация о применении комплекса программного обеспечения с использованием полевой модели динамики пожара для проведения расчетов пожаров в зданиях и помещениях атомных станций. Приведены необходимые обоснования для использования возможности данного комплекса при проведении расчетов пожаров в зданиях и помещениях различного назначения.
Цель работы – проведение анализа различных методов моделирования пожара, области их применения, использования комплекса программного обеспечения полевой модели динамики пожара для определения динамики параметров опасных факторов пожара в помещениях сложной конфигурации, с неравномерно распределенной пожарной нагрузкой, сложным режимом газообмена, а также при решении задачи определения безопасных расстояний, обеспечивающих невозможность распространения пожара между элементами оборудования.
Материалы и методы. Разработан и верифицирован комплекс программного обеспечения, позволяющий проводить расчеты с использованием полевой модели динамики пожара. Рассмотрены основы полевого метода моделирования пожара в помещениях различного назначения и особенности его применения для моделирования пожаров. Авторы статьи сопроводили представленный аналитический материал примерами результатов моделирования пожара в реальных помещениях АЭС.
Результаты. На основании проведенного анализа различных методов моделирования динамики развития и распространения опасных факторов пожара показана возможность использования различных методов моделирования пожара при анализе пожарной опасности зданий и помещений. Показаны преимущества методики полевого моделирования для проведения расчетов локальных параметров пожара. Приведена информация о программных кодах, применяющихся для расчета динамики пожаров и оценки теплового воздействия пожаров на строительные конструкции.
Выводы. Показано применение полевой модели динамики пожара для проведения расчетов опасных факторов пожара в различных зданиях, помещениях и на открытых площадках. Расчеты с использованием предложенной полевой модели позволяют обосновать достаточность огнестойкости строительных конструкций зданий и помещений различного назначения исходя из обеспечения нераспространение пожара за пределы пожарной зоны в течение расчетного времени свободного выгорания всей пожарной нагрузки.
Ключевые слова
Для цитирования:
Пуцев Д.И., Кривцов Ю.В., Грошев Ю.М., Лобанова Н.А. Оценка возможности применения полевого моделирования пожара для проведения расчетов пожаров в зданиях и помещениях. Вестник НИЦ «Строительство». 2023;37(2):37-70. https://doi.org/10.37538/2224-9494-2023-2(37)-37-70. EDN: ETZDYW
For citation:
Putsev D.I., Krivtsov Yu.V., Groshev Yu.M., Lobanova N.A. Evaluating feasibility of field modeling of fire to calculate fire characteristics in buildings and premises. Bulletin of Science and Research Center of Construction. 2023;37(2):37-70. (In Russ.) https://doi.org/10.37538/2224-9494-2023-2(37)-37-70. EDN: ETZDYW
Введение
В последние годы как в России, так и за рубежом (Швеция, Великобритания, США, Канада, Испания, Япония, Австралия и др.) наметился переход к гибкому (объектно-ориентированному) нормированию, которое позволяет наиболее оптимальным образом обеспечить пожарную безопасность объекта с учетом его функциональных особенностей, в отличие от «жесткого» нормирования, предписывающего строгое соблюдение требований пожарной безопасности, установленных в нормативных правовых актах и нормативных документах по пожарной безопасности. Гибкое (объектно-ориентированное) нормирование предполагает многоуровневую систему требований и методов, в которой установленные критерии достижения цели должны быть подтверждены расчетно-аналитическими или экспериментальными методами [1]. В связи с этим особую важность приобретают расчетно-аналитические обоснования пожарной безопасности объектов защиты, выполняющиеся в поддержку принимаемых решений. Например, в области атомной энергетики для подтверждения достаточности уровня противопожарной защиты энергоблока предписывается выполнение специального анализа – анализа влияния пожаров и их последствий на безопасный останов и расхолаживание реакторной установки, локализацию и контроль радиоактивных выбросов в окружающую среду. В ходе выполнения этой работы для каждого энергоблока осуществляется проверка достаточности принятых проектом пределов огнестойкости противопожарных преград, являющихся границами пожарных зон, и безопасных (предельных) расстояний между элементами оборудования, обеспечивающих невозможность потери резервируемых элементов безопасности по общей причине пожара. При этом обоснование выполняется из условия, что указанные противопожарные преграды и безопасные расстояния должны обеспечивать нераспространение пожара за пределы пожарной зоны в течение времени полного свободного (без учета воздействия на пожар огнетушащих веществ) выгорания пожарной нагрузки, то есть рассматривается вариант отказа автоматических установок пожаротушения. Таким образом, очевидно, что анализ влияния пожаров на безопасность энергоблока требует серьезного расчетно-аналитического обоснования, основанного на применении различных расчетных методов моделирования пожаров. При этом особое значение приобретают вопросы верификации моделей и обоснованности их применения для оценки пожарной опасности и обоснования достаточности систем противопожарной защиты конкретных объектов.
Расчетные методы включают в себя:
- эмпирические методики оценки динамики пожара;
- интегральный метод расчета среднеобъемных параметров пожара;
- методику расчета локальных параметров пожара (полевое моделирование);
- методику определения требований к огнестойкости конструкций.
Эмпирические методики оценки динамики пожара
Простейший пример использования эмпирических методик оценки динамики пожара – проведение расчетов на основе оценки продолжительности «стандартного температурного режима». Модель стандартного температурного режима пожара описана в работе [2].
Стандартная температурная кривая представлена на рис. 1. Зависимость продолжительности стандартного пожара от удельной пожарной нагрузки анализируемых помещений приведена на графике (рис. 2).
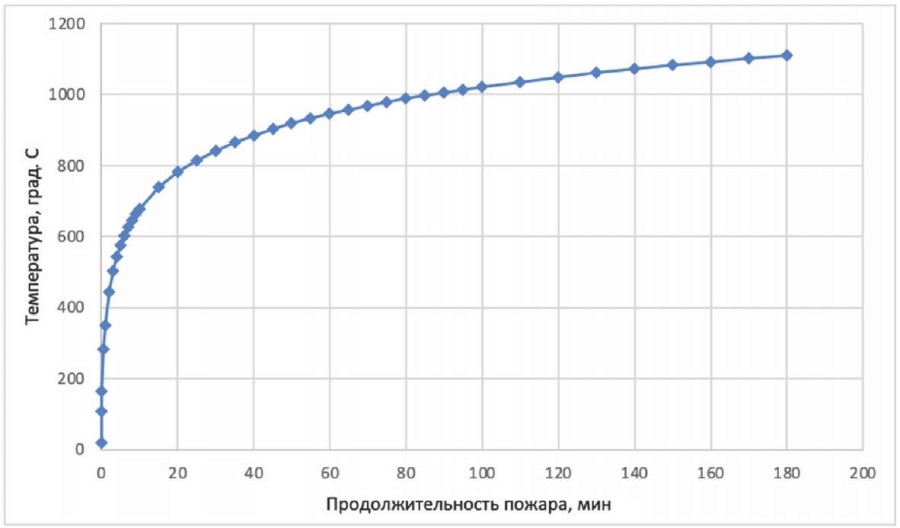
Рис. 1. Зависимость температуры стандартного пожара (°C) от времени, мин
Fig. 1. Dependence of standard fire temperature (°C) on time, min
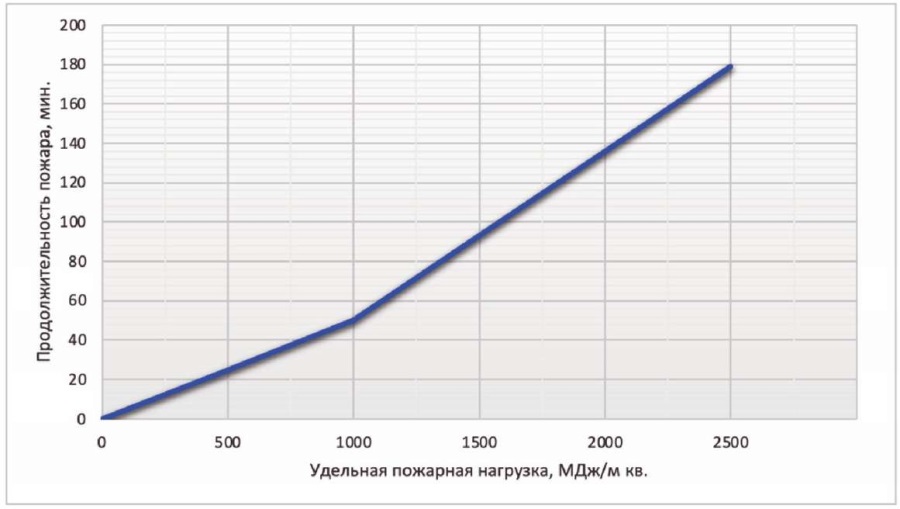
Рис. 2. Зависимость продолжительности стандартного пожара (мин) от удельной пожарной нагрузки, МДж/м2
Fig. 2. Dependence of standard fire duration (min) on fire load density, MJ/m 2
Определив удельную пожарную нагрузку в помещении, по графику на рис. 2 можно найти соответствующую продолжительность стандартного пожара, затем по графику на рис. 1 для найденной продолжительности стандартного пожара можно найти соответствующую температуру в помещении.
Консервативные подходы, определенные в данной методологии, не учитывают мероприятий по тушению, ограничений по доступу кислорода в зону пожара для герметичных или частично герметичных помещений и используются в пределах своей области определения, установленной по условиям проводимых экспериментов, на основе которых была установлена зависимость продолжительности стандартного пожара от удельной пожарной нагрузки, а именно:
- горение преимущественно твердой горючей нагрузки;
- доступ кислорода в зону пожара не ограничен;
- максимальная удельная пожарная нагрузка в помещении не превышает 1500 МДж/м2.
В существующей практике выполнения анализов влияния пожаров и их последствий на безопасный останов и расхолаживание реакторной установки, локализацию и контроль радиоактивных выбросов в окружающую среду для различных энергоблоков АЭС расчеты требуемой огнестойкости методом оценки продолжительности «стандартного температурного режима» используются как скрининговый критерий при проведении консервативной оценки требований к огнестойкости ограждающих конструкций для помещений с относительно невысокой пожарной нагрузкой. В данном проекте к таким помещениям можно отнести помещения с пожарной нагрузкой не более 1500 МДж/м2.
Другими примерами использования эмпирических методик оценки динамики пожара являются методы расчета температурного режима пожара в помещениях зданий различного назначения и метод расчета требуемого предела огнестойкости, изложенные в ГОСТ Р 12.3.047-12 ССБТ [3]. Указанные методы расширяют подход, описанный выше, с целью получить более точные количественные требования к пределам огнестойкости строительных конструкций с учетом фактических характеристик пожарной нагрузки и воздухообмена помещения с окружающей средой. Методы разработаны ВНИИПО на основе результатов обобщения экспериментальных данных по пожарам в жилых помещениях. Поскольку областью определения данных методов являются помещения, имеющие воздухообмен с окружающей средой при степени проемности (рассчитанной по отношению площади проемов к площади пола) в пределах 3–33 %, их применение для расчетов пожаров в помещениях пожарных зон АЭС, имеющих значительные ограничения по связи с окружающей средой, лежит за пределами области определения.
Интегральный (зонный) метод расчета среднеобъемных параметров пожара
Методы расчета среднеобъемных параметров пожара рекомендованы в качестве аналитических методов определения требований к границам пожарных зон для АС в тех случаях, когда полуэмпирические расчетные методы не могут быть использованы из-за ограничений их области применения.
Практически важные результаты моделирования пожаров на уровне усредненных характеристик можно ожидать в том случае, когда газовую среду с достаточной степенью достоверности можно считать однородной, следовательно, отсутствуют значительные градиенты определяющих параметров, что дает основание описать их среднеобъемными характеристиками (т. е. среднеобъемные и локальные значения параметров мало отличаются между собой). Приведенные условия, ограничивающие применение интегрального метода моделирования, означают, что этот метод можно использовать в том случае, когда при пожаре в помещении существует хорошее перемешивание продуктов горения и поступающего воздуха, а горение происходит во всем объеме помещения. Такое состояние характерно для объемных пожаров в развивающейся, развитой и затухающей стадиях пожара, в условиях горения распределенной пожарной нагрузки.
Наиболее эффективно интегральный метод моделирования используется для прогнозирования поведения строительных конструкций в условиях пожара, поскольку прогрев конструкций в большинстве случаев наиболее интенсивен в развитой стадии пожара. Проведенные исследования локальных пожаров и начальной стадии пожара позволили определить границы применения интегрального моделирования для решения практических задач пожарной безопасности и, в частности, для исследования устойчивости строительных конструкций в условиях пожара.
Метод расчета динамики пожара на основе среднеобъемной модели строится на основе уравнений материального баланса и баланса энергии для исследуемого помещения. Расчетная схема, которая приводится по [4], представлена на рис. 3.
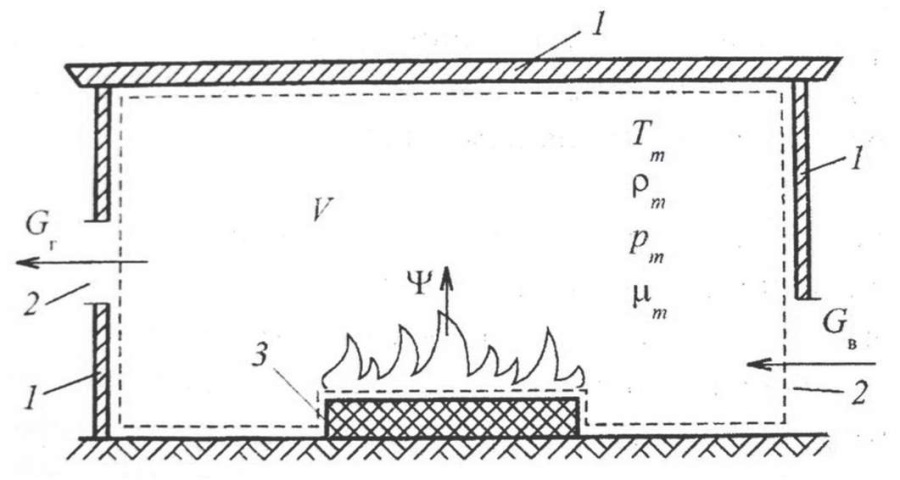
Рис. 3. Схема термодинамической системы пожара в помещении:
1 – ограждения; 2 – проемы (окна, двери); 3 – горящий материал;
GГ – расход уходящих газов; GВ – расход поступающего холодного воздуха;
ψ – скорость выгорания материала; Tm – среднемассовая температура газовой среды;
Рm – средняя по объему плотность газовой среды; pm – среднеобъемное давление;
μm – среднеобъемная оптическая плотность дыма.
Контрольная поверхность обозначена пунктиром
Fig. 3. Schematic diagram for thermodynamic system of fire in premises:
1 – fencing; 2 – openings (windows, doors); 3 – burning material;
GГ – exhaust gas flow rate; GB – incoming cold air flow rate;
ψ – material combustion rate; Tm – bulk temperature of gaseous medium;
Рm – average volume density of gaseous medium; pm – volume-averaged pressure;
μ m – volume-averaged optical density of smoke.
The reference surface is indicated by a dotted line
Уравнение материального баланса для газовой среды в помещении:
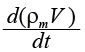 = GВ+ ψ – GГ .(1)
= GВ+ ψ – GГ .(1)
Уравнение баланса массы кислорода:
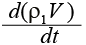 = x1В GВ – x1n1GГ – ψL1η.(2)
= x1В GВ – x1n1GГ – ψL1η.(2)
Уравнение баланса продукта горения:
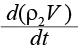 = ψL2η – x2n2GГ .(3)
= ψL2η – x2n2GГ .(3)
Уравнение энергии пожара имеет вид (предполагается, что кинетическая энергия движения газовой среды в помещении пренебрежимо мала по сравнению с ее внутренней энергией, а потоки массы газов через некоторые участки контрольной поверхности (проемы) характеризуются тем, что в них удельная кинетическая энергия газа пренебрежимо мала по сравнению с удельной энтальпией):
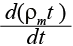 = ψQHpη + iГ ψ + сPВ TB GВ – сP Tm m GГ – Qw,(4)
= ψQHpη + iГ ψ + сPВ TB GВ – сP Tm m GГ – Qw,(4)
где iГ – энтальпия продуктов горения;
сPВ – изобарная теплоемкость воздуха при постоянном давлении;
TВ – температура воздуха;
QW – теплота, уходящая в ограждающие конструкции.
Результат интегрирования системы уравнений (1)–(4) в комплексе с начальными условиями состояния среды до начала пожара используется в качестве расчетной модели для оценки опасных факторов пожара на начальной стадии пожара с учетом ряда дополнительных предположений:
- отсутствия притока воздуха в помещение пожара;
- постоянного давления в помещении;
- неизменности коэффициента теплопотерь (отношения теплопотерь в конструкции к тепловыделению пожара);
- неизменности молекулярной массы газовой среды;
- использования эмпирической формулы экспоненциального распределения параметров среды по высоте помещения.
Описанная среднеобъемная модель используется в расчетно-аналитических обоснованиях динамики пожаров на АЭС для моделирования развития пожара в электротехнических помещениях и оценки термического воздействия на их конструкции. Из вышеперечисленных предположений используется только предположение о постоянстве давления внутри помещения, что позволяет корректно использовать модель, являющуюся следствием точных уравнений сохранения массы и энергии на различных стадиях развития пожара. Постоянство давления с достаточно высокой степенью следует из отсутствия мероприятий по герметизации дверей, люков, клапанов (за исключением гермообъема здания реактора, для которого модель не применяется), что ведет к невозможности удержания давления пожара при его развитии на различных стадиях. Наличие преимущественно твердых горючих материалов в электротехнических помещениях, условно герметичных при закрытых дверях и вентиляционных клапанах, обусловливает относительно медленное развития пожара и выравнивание давления с окружающими помещениями через неплотности.
Расчеты параметров пожара для указанных помещений проводятся путем совмещения рассматриваемой среднеобъемной модели для расчетов параметров газовоздушной среды и полевой модели динамики пожара, представленной ниже. Характеристики газовоздушной среды в помещении определяются в результате непосредственного расчета по уравнениям баланса (1)–(4). Тепловые потоки в окружающие конструкции также получаются в результате расчетного решения сопряженной задачи теплообмена с учетом конвективной и излучательной составляющих. При расчетах используется еще одно дополнительное предположение – отсутствие одновременно входящих и выходящих потоков газовоздушной среды. Данные потоки определяются, при известной степени негерметичности, разностью давления анализируемого и окружающих помещений. Двухсторонние возвратно поступательные потоки возникают только в помещениях с достаточно высокой степенью проемности. Критерием их существования является степень проемности около 4–5 %. Естественно, что помещения АЭС, в которых постоянно осуществляется автоматический контроль закрытого состояния дверей, а газообмен происходит только через неплотности, имеют условную проемность на порядок меньше указанной критической величины.
Методика расчета локальных параметров пожара (полевое моделирование)
В тех случаях, когда требуется рассчитать локальные параметры развития пожара или область применения, не позволяется использовать эмпирические или среднеобъемные модели, в практике моделирования пожара на АЭС для расчета динамики пожара применяется созданная во ВНИИПО полевая модель [1]. Это, прежде всего, относится к расчетам пожара в больших помещениях, помещениях с неравномерно распределенной пожарной нагрузкой и сложным режимом газообмена, к задаче определения безопасных расстояний для оборудования систем безопасности. Данная модель создана с учетом требований рекомендаций по применению методов полевого моделирования.
Полевой метод является наиболее универсальным из существующих детерминистических методов, поскольку он основан на решении уравнений в частных производных, выражающих фундаментальные законы сохранения в каждой точке расчетной области. С его помощью можно рассчитать температуру, скорость, концентрацию компонентов смеси и т. д. в каждой точке расчетной области. В связи с этим полевой метод может использоваться:
- для проведения научных исследований в целях выявления закономерностей развития пожара;
- для проведения сравнительных расчетов в целях апробации и совершенствования менее универсальных зональных и интегральных моделей, проверки обоснованности их применения;
- для выбора рационального варианта противопожарной защиты конкретных объектов.
В своей основе полевой метод не содержит никаких априорных допущений о структуре течения, и в связи с этим он принципиально применим для рассмотрения любого сценария развития пожара.
Вместе с тем следует отметить, что его использование требует значительных вычислительных ресурсов. Это накладывает ряд ограничений на размеры рассматриваемой системы и снижает возможность проведения многовариантных расчетов. Поэтому перечисленные выше методы моделирования также являются важными инструментами в оценке пожарной опасности объектов в тех случаях, когда они обладают достаточной информативностью и сделанные при их формулировке допущения не противоречат картине развития пожара.
Однако можно утверждать, что поскольку априорные допущения зонных моделей могут приводить к существенным ошибкам при оценке пожарной опасности объекта, предпочтительно использовать полевой метод моделирования в следующих случаях:
- для помещений сложной геометрической конфигурации, а также помещений с большим количеством внутренних преград;
- для помещений, в которых один из геометрических размеров гораздо больше остальных;
- для помещений, где существует вероятность образования рециркулярных течений без формирования верхнего прогретого слоя (что является основным допущением классических зонных моделей);
- в иных случаях, когда другие модели являются недостаточно информативными для решения поставленной задачи, либо есть основания считать, что развитие пожара может существенно отличаться от априорных допущений.
Данная математическая модель пожара предусматривает решение системы уравнений газодинамики и теплообмена с учетом моделирования процессов горения и переноса тепла излучением.
Система уравнений полевой модели имеет следующий вид:
Уравнение неразрывности газовой смеси
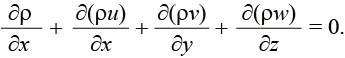
Уравнения движения газовой смеси в проекции на оси координат (записаны для декартовой системы)

где тензор напряжений
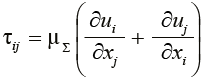 ,
,
i, j, k =1, 2, 3.
Уравнение энергии
 .
.
Уравнения переноса для различных компонент газовой смеси
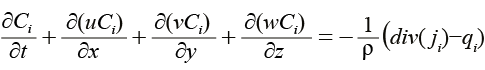 .
.
Уравнения состояния компонентов газовоздушной смеси
ρ = F(P*, T, Ci),
где x, y, z – пространственные координаты;
u, v, w – компоненты скорости газовоздушных потоков в направлении координат x, y, z;
μΣ, λΣ, DΣ – суммарные (молекулярные и турбулентные) коэффициенты вязкости, теплопроводности и диффузии соответственно;
p – локальное давление;
P* – среднеобъемное давление;
ρ – плотность среды;
T, h – температура и энтальпия;
Ci – массовая концентрация соответствующего компонента;
q – удельный тепловой поток;
qv – тепловыделение в единице объема;
ji – удельный массовый поток i-го компонента;
qi – скорость образования (поглощения) i-го компонента в единице объема.
Система уравнений решается совместно с уравнениями диффузионных потоков:

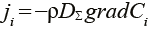 .
.
Для определения турбулентного переноса массы и энергии используется гипотеза турбулентной вязкости Буссинеска. При расчете распределения коэффициента турбулентной вязкости применяется k-ε модель турбулентности. В этой модели распределение коэффициента турбулентной вязкости μ находится из решения двух дифференциальных уравнений для кинетической энергии к турбулентности и скорости ее дисcипации ε:
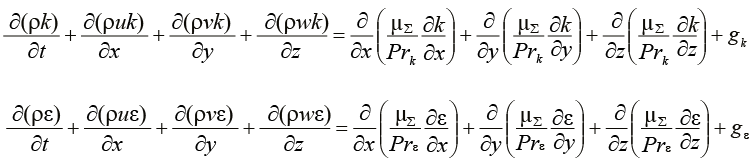
Источниковые члены в данных уравнениях описываются следующими зависимостями, включающими генерацию турбулентности при естественной конвекции:
gk = Pk + Gk – ε
gе = C1ε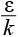 (Pk + Gk)(1 + C3εRf ) – C2ε
(Pk + Gk)(1 + C3εRf ) – C2ε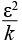
Gk =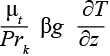
Pk =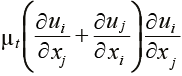
Rf = – Gk /(Pk+Gk)
|
Значения констант |
|||||
|
Cμ |
C1ε |
C2ε |
C3ε |
Prk |
Prε |
|
0,09 |
1,44 |
1,92 |
0,8 |
1,0 |
1,3 |
Коэффициент турбулентной вязкости находится по соотношению:
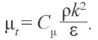
Эффективные турбулентные потоки тепла, массы компонент, кинетической энергии турбулентности и скорости ее диссипации рассчитываются на основе аналогии турбулентной вязкости и турбулентных коэффициентов диффузии при постоянных турбулентных числах Prt (Sct ):
qt = –λt grad T, где λt = μ t /Prt и т. д.
Модель горения
Для описания физико-химических процессов при горении используются два подхода: моделирование химических реакций или задание эквивалентных горению тепловых и массовых потоков в качестве граничных условий на поверхностях горения.
Моделирование химических реакций горения
Реально протекающие химические процессы горения аппроксимируются одноступенчатой химической реакцией горения:
топливо(fu) + s окислитель(оx) = (1 + s) продукты (pr).
При этом предполагается, что скорость протекания процесса горения лимитируется не скоростью протекания самой химической реакции, а скоростью взаимной диффузии компонентов, то есть горение носит явно выраженный диффузионный характер.
Массовая скорость выгорания топлива в единице объема Rfu рассчитывается по формуле:
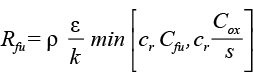 .
.
Требуемые для расчета скорости реакции локальные значения кинетической энергии турбулентности к и скорости ее диссипации ε находятся в процессе решения уравнений, входящих в модель турбулентности.
Методика определения требований к огнестойкости конструкций
Эмпирические методы расчета режима пожара и степени воздействия опасных факторов пожара на конструкции во многих случаях дают непосредственную оценку эквивалентной (по степени воздействия) продолжительности пожара на строительные конструкции. При проведении расчетов динамики пожара в помещении на основе среднеобъемных или полевых дифференциальных уравнений возможны более точные расчеты параметров развития пожара, но непосредственных данных об эквивалентной продолжительности пожара из решения не следует. В этих случаях возможны два подхода к определению требований по огнестойкости:
- по результатам моделирования пожара определяются его продолжительность и динамика среднеобъемных или локальных характеристик. На основе эмпирических методов определяется эквивалентная продолжительность пожара для различных типов строительных конструкций;
- производится решение сопряженной задачи теплообмена, т. е. в процессе моделирования пожара проводится непосредственный расчет режимов прогрева строительных конструкций. По результатам максимального (среднего или локального) прогрева конструкций оценивается возможность ее повреждения в условиях реального пожара. В этом случае необходим более сложный анализ прочности в условиях прогрева, в то же время дающий в общем случае более точные результаты, т. к. определяется фактическая огнестойкость, а не пересчет на результаты испытаний в стандартных условиях.
Программные коды, применяющиеся для расчета динамики пожаров и оценки теплового воздействия пожаров на строительные конструкции
При проведении расчетов по эмпирическим расчетным методикам применяются расчеты по зависимостям, заданным в электронных таблицах с характеристиками помещений. Используется также реализация в виде программной оболочки для MS Windows, написанная на языке С (Borland C++, ver. 4.0).
При проведении расчетов среднеобъемных характеристик пожара в помещении используется программа FVolume. Программный код написан на языке FORTRAN 77. Результаты расчетов верифицировались на основе экспериментальных данных о динамике пожара и существующих аналитических решений обыкновенных дифференциальных уравнений.
При моделировании пожара для расчета температуры поверхности конструкции и динамики распределения поля температуры внутри конструкции используется программный код 1Dconduction, предназначенный для решения одномерной нестационарной задачи теплопроводности с учетом переменных теплофизических характеристик материала. Код реализован на языке С++. Верификация проводилась на основе сравнения с результатами аналитического решения одномерной нестационарной задачи теплопроводности.
Для реализации описанной выше трехмерной полевой модели динамики пожара во ВНИИПО разработан комплекс программ Fire Dynamics. Программный комплекс позволяет проводить моделирование пожаров как в помещениях различной геометрии, так и на открытых промышленных площадках. Программное обеспечение написано на объектно-ориентированном языке С++. Комплекс программ выполнен в базовой (научной) и инженерной версиях. Инженерная версия включает реализацию некоторых полуэмпирических зависимостей, описывающих изменение параметров горения (скорости выгорания горючих материалов, скорости распространения пламени по горючей нагрузке и т. д.) в зависимости от условий развития пожара.
Параметры модели и программный код прошел основную и дополнительную (применительно к условиям моделирования задач на АЭС) верификации [5][6].
Отчет о верификации программного средства Fire Dynamics [5] разработан в соответствии с требованиями РД 03-33-2008 «Инструкция об организации проведения экспертизы программных средств, применяемых при обосновании и (или) обеспечении безопасности объектов использования атомной энергии» [7] и РД 03-34-2000 «Требования к составу и содержанию отчета о верификации и обосновании программных средств, применяемых для обоснования безопасности объектов использования атомной энергии» [6]. Отчет является основным документом, обосновывающим способность программного средства Fire Dynamics моделировать и рассчитывать параметры опасных факторов пожара в зданиях, сооружениях, помещениях и промплощадках АЭС. Целью отчета являлось обоснование возможности использования предлагаемого к рассмотрению программного средства Fire Dynamics в заявленной области применения путем сравнения с экспериментальными данными.
Программное средство (ПС) не имеет самостоятельных модулей. Автором ПС является д-р техн. наук Пуцев Дмитрий Игоревич.
Организацией-заявителем является Научно-технический центр «Промышленная и пожарная безопасность». Программный комплекс используется Научно-техническим центром «Промышленная и пожарная безопасность» (ООО «НТЦ ППБ») и Научно-исследовательским институтом противопожарной обороны (ФГБУ ВНИИПО МЧС России).
Сведения об операционной системе, языке (языках) программирования, требованиях к ЭВМ, на которых возможно выполнение расчетов с применением ПС: операционные системы: Windows XP SP3, Windows 7; язык (языки) программирования: С++ стандартная версия (компиляторы Microsoft Visual, Borland или др.).
Программное средство предназначено для моделирования пожара на АЭС с целью получения локальных значений опасных факторов пожара и оценки уровня их воздействия на оборудование и конструкции станции. ПС предполагается использовать для проектных или эксплуатационных расчетов, в том числе для обоснования безопасности объекта использования атомной энергии (ОИАЭ) в документах, представляемых в надзорные органы РФ в рамках процедуры лицензирования ОИАЭ. По погрешности расчетов ПС не относится к классу реперных, а используется в качестве средства научных и инженерных расчетов.
Расчетными параметрами являются локальные значения температуры, составляющих скорости газовоздушной среды в объеме, концентраций продуктов горения и кислорода, тепловые потоки; среднеобъемные значения температуры, давления, концентрации компонент газовоздушной среды.
ПС позволяет достигать условий сходимости и устойчивости решения. Сходимость и устойчивость анализировались: аналитическим путем для линейных аналогов одномерных уравнений переноса; проверкой симметричности и асимптотичности решения при задании соответствующих начальных и граничных условий; обнаружением волновой неустойчивости решения при контроле нижней границы расчетных параметров (локальные значения температур или концентраций меньше (для кислорода – больше) начальных).
Точность вычисления расчетных параметров в рамках используемых моделей может быть доведена до 2–5 % путем подбора пространственной сетки и шагов интегрирования. Получение более точного решения не имеет смысла, поскольку общая погрешность определяется погрешностью используемых моделей и экспериментальных параметров.
В ходе верификации выполнялось следующее тестирование:
Тестовый пример № 1 – расчет и эксперимент по горению кабелей в кабельном тоннеле.
Во ВНИИПО была проведена серия экспериментов по развитию пожара в кабельных помещениях. Для верификации математических моделей и программных кодов были выполнены расчеты динамики пожара кабелей и сравнение результатов с данными экспериментов для пожара, возникающего на восьми кабельных трассах. Горение кабельных трасс инициировалось керосином, залитым в противень размером 0,5 × 0,5 м в количестве 10 литров. Были проведены эксперименты для различной пожарной нагрузки кабельных трасс, различных режимов газообмена и вентиляции. Были также проведены дополнительные эксперименты с целью выявить влияние горения керосина на динамику развития пожара с целью оценки степени влияния мощности и длительности действия источника зажигания. Сравнение экспериментальных и расчетных данных показали возможность использования модели и программного кода для моделирования пожара в помещениях больших объемов. Максимальное расхождение расчетных и экспериментальных данных (относительная погрешность) составило 22 %.
Тестовый пример № 2 – расчет и эксперимент по горению горючей жидкости в машинном зале ТЭС.
Специалистами ВНИИПО были проведены натурные эксперименты по горению ГЖ в машинном зале. Эксперимент проводился на действующей ТЭС в период планового ремонта. Задачей эксперимента являлось определение режима нарастания слоя продуктов горения в объеме зала и оценка характеристик (температура, видимость) в области продуктов горения. Очаг пожара представлял собой противень с керосином размером 4,5 × 1,5 м. Сравнение экспериментальных и расчетных данных показало возможность использования модели и программного кода для моделирования пожара в помещениях больших объемов. Максимальное расхождение расчетных и экспериментальных данных (относительная погрешность) составило 16 %.
Тестовый пример № 3 – расчет и эксперименты по горению шкафов с электронной и электротехнической аппаратурой, исследования воздействия ОФП на шкафы электронных и электротехнических устройств.
Во ВНИИПО была создана установка для оценки воздействия опасных факторов пожара на системы управления защитой реактора (СУЗ). В качестве условий для испытания шкафов СУЗ на устойчивость к воздействию продуктов горения был выбран наиболее реальный и наиболее жесткий случай подвода продуктов горения из специального генератора дыма непосредственно под середину устройства. В качестве горючей нагрузки в генераторе дыма использовался наиболее характерный и наиболее опасный с точки зрения выделения продуктов горения материал – изоляция кабелей. Серия экспериментов была посвящена исследованию воздействия теплового излучения и температуры на отдельные элементы электронных устройств. Проведены два огневых эксперимента по исследованию режимов горения стоек с электронной аппаратурой. Для условий, близких к условиям экспериментов, проведено расчетное моделирование горения. Погрешность расчета максимальной температуры пламени по сравнению с экспериментальными данными составила 17 %. Поскольку данные о скорости выгорания и режимах отказов элементов стоек управления являются уникальными, они непосредственно используются при приведении расчетов.
По итогам верификации отмечено, что описанные методы определения эквивалентной продолжительности пожара для несущих и ограждающих конструкций не нуждаются в доработке для использования на АЭС и могут быть использованы для определения требований к границам пожарных зон. В работе показано, что приведенные методы расчета динамики пожара и требования к огнестойкости строительных конструкций являются достаточно достоверными, отличаются относительно невысокой трудоемкостью при использовании, но имеют ограниченную область применения. Поскольку данные расчетные методы построены на основе результатов экспериментальных исследований, область применимости приведенных зависимостей определяется интервалом варьирования различных параметров в ходе соответствующих экспериментов. Область применения конкретных зависимостей описана в оригинальных работах по исследованию динамики пожара в помещениях.
Результаты
В рамках работ по обеспечению пожарной безопасности АЭС была разработана методика расчета динамики возможных пожаров для оценки воздействия опасных факторов на оборудование, в первую очередь систем безопасности, и на строительные конструкции атомных станций.
На основе выполненных расчетов с применением полевой модели динамики пожара были предложены и внедрены мероприятия по обеспечению пожарной безопасности действующих АЭС России: Балаковской, Белоярской, Билибинской, Волгодонской, Калининской, Кольской, Курской, Ленинградской, Ростовской, Нововоронежской и Смоленской, а также новых строящихся отечественных и зарубежных АЭС: Тяньваньской АЭС в Китае, АЭС Кудан-Кулам в Индии, АЭС «Бушер» в Иране, Белорусской АЭС.
Расчетные результаты вошли в проектную документацию и отчеты по безопасности, прошедшие в установленном порядке рассмотрение в надзорных органах (Федеральная служба по экологическому, технологическому и атомному надзору, Государственный пожарный надзор) и Главной государственной экспертизой проектов, что является убедительным доказательством возможности ее дальнейшего применения.
Анализ результатов расчетов
Далее в качестве примеров использования методов моделирования пожара представлены некоторые результаты моделирования пожаров в пожароопасных помещениях АЭС.
Пример 1. Кабельная шахта категории В1 по пожарной опасности:
- удельная пожарная нагрузка в помещении 4077,7 МДж/м2;
- геометрические характеристики помещения: площадь 6 м2, высота 3,6 м.
Анализ термического воздействия пожара на несущие и ограждающие конструкции помещения проводится на основе математического моделирования с применением описанной выше интегральной модели расчета среднеобъемных параметров пожара.
При анализе предполагалось несрабатывание системы пожаротушения вследствие отказа. При этом предполагается нормальная работа других независимых элементов противопожарной защиты:
- закрытие огнезадерживающих клапанов вентиляции (срабатывающих как по сигналу автоматической установки пожаротушения, так и по пассивному признаку – плавлению легкоплавких вставок);
- закрытое состояние дверей (параметр, контролируемый датчиками контроля закрытого состояния дверей).
Вследствие выполнения вышеуказанных условий рассматриваемые помещения могут считаться условно герметичными. Расчеты проводятся для кругового распространения пожара в начальной стадии, перехода пожара в объемную стадию и максимальных значений теплоты сгорания и скорости выгорания материала.
Расчет ведется для толщины ограждающих конструкций – 200 мм. Выполняется оценка прогрева защитного слоя бетона толщиной 20 мм с целью подтверждения условия обеспечения устойчивости конструкций к термическому воздействию пожара в исследуемом помещении с учетом его фактических пожарных нагрузок. Главным условием обеспечения такой устойчивости является прогрев защитного слоя бетона до температур, не превышающих 500 °C, что гарантирует прогрев арматуры до температур, не превышающих этот показатель (максимальная температура на необогреваемой стороне конструкции не играет принципиальной роли при полученных длительностях пожара для рассматриваемых типов конструкций, что хорошо видно на графиках динамики распределения абсолютной температуры по сечению окружающих конструкций, рис. 4). Полученные результаты представлены на рис. 4–9 и в табл. 1.
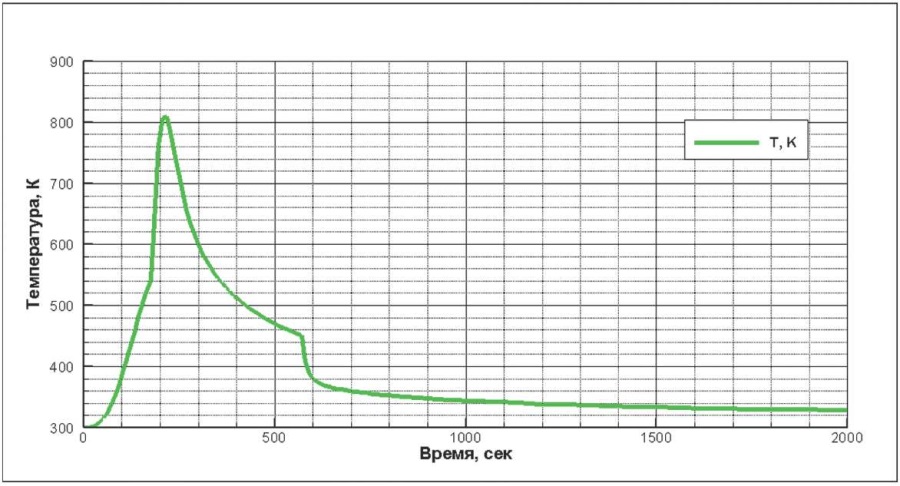
Рис. 4. Динамика среднеобъемной абсолютной температуры при пожаре, К
Fig. 4. Dynamics of volume-averaged absolute temperature in case of fire, K

Рис. 5. Динамика изменения массовой концентрации кислорода
Fig. 5. Dynamics of oxygen mass concentration
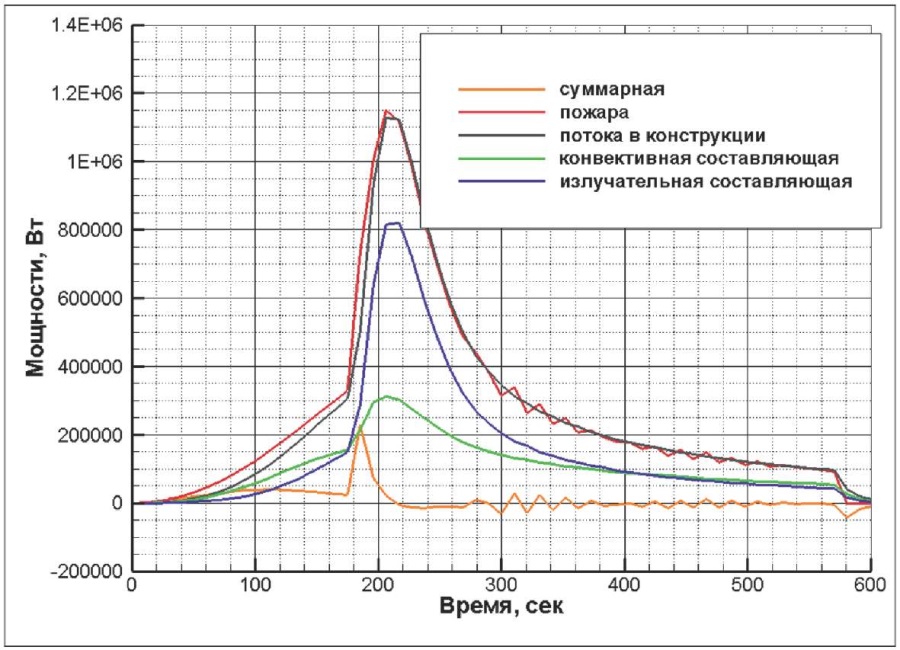
Рис. 6. Динамика изменения мощности энергетических потоков, Вт
Fig. 6. Dynamics of power flow capacity, W
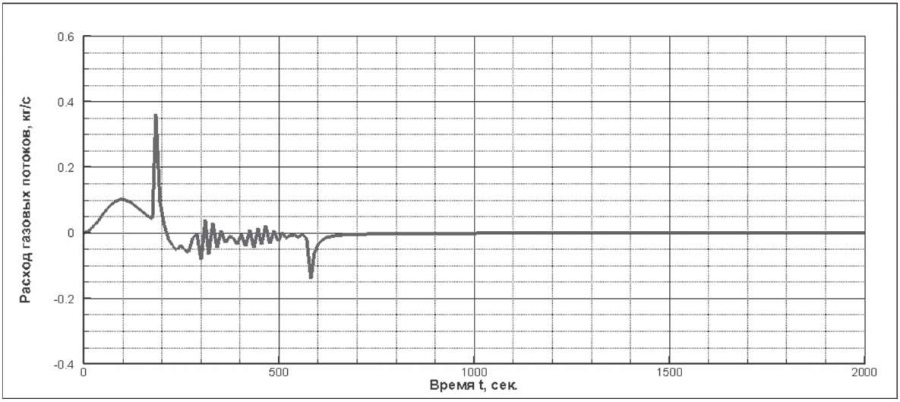
Рис. 7. Расход выходящего (входящего) через неплотности газового потока, кг/c
Fig. 7. Leak rate of outgoing (incoming) gas flow, kg/s
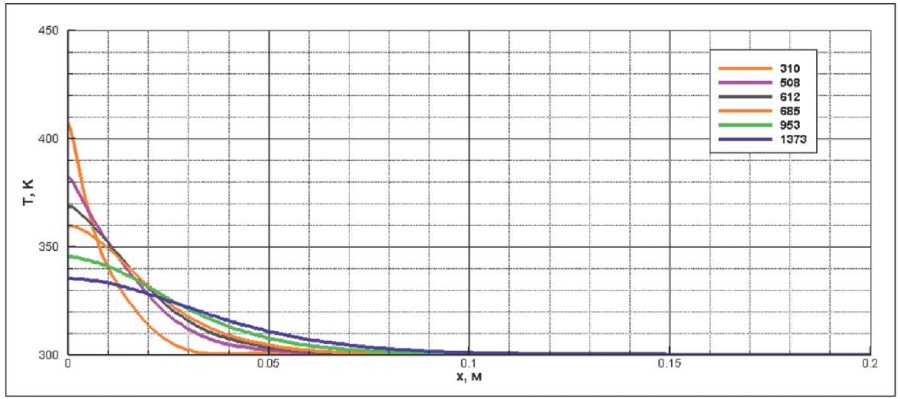
Рис. 8. Динамика распределения абсолютной температуры по сечению окружающих конструкций, К, время от начала пожара, с
Fig. 8. Dynamics of cross-section distribution of absolute temperature over surrounding structures, K, time from outbreak of fire, s
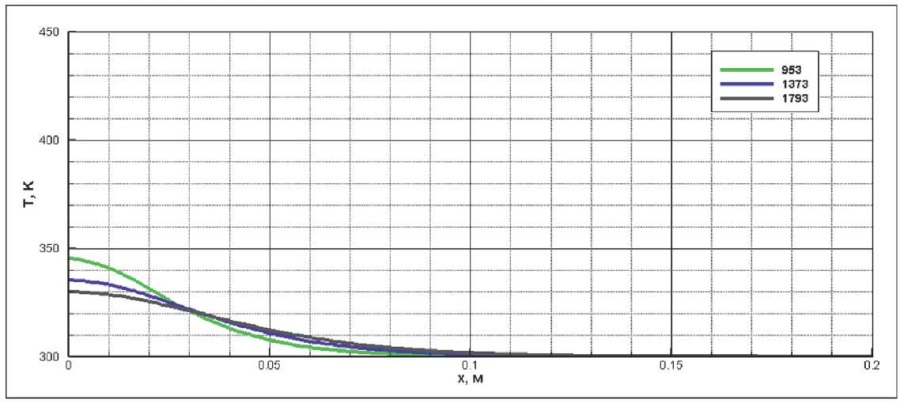
Рис. 9. Динамика распределения абсолютной температуры по сечению окружающих конструкций, К, время от начала пожара, с
Fig. 9. Dynamics of cross-section distribution of absolute temperature over surrounding structures, K, time from outbreak of fire, s
Таблица 1
Результаты моделирования пожара в кабельной шахте
Table 1
Results of cable duct fire modeling
|
Наименование помещения |
Площадь, м2 |
Высота, м |
Удельная пожарная нагрузка, МДж/м2 |
Максимальная температура поверхности конструкции, K |
Время достижения максимальной температуры поверхности, с |
Максимальная температура защитного слоя, K |
Время достижения максимальной температуры защитного слоя, с |
Время начала объемного пожара, с |
|
Кабельная шахта № 4 |
6,0 |
3,6 |
4077,7 |
422 |
246 |
337 |
736 |
181 |
Таблица 2
Исходные данные по пожарным нагрузкам
Table 2
Input data on fire loads
|
Наименование пожарной нагрузки |
Масса пожарной нагрузки, кг |
Низшая теплота сгорания, МДж/кг |
|
Дизельное топливо |
249 |
43,59 |
|
Резина |
846 |
43,89 |
|
Смазочные материалы |
18 |
41,87 |
|
Пенополиуретан |
4 |
24,3 |
|
Полиэтилен |
1,8 |
47,14 |
|
Поливинилхлорид |
2,6 |
14,31 |
|
Картон |
2,5 |
13,4 |
|
Искусственная кожа |
1,8 |
17,76 |
Из результатов расчета для помещения шахты следует:
Около 180 с происходит линейное распространение пожара, потом пожар переходит в объемную стадию. Рост температуры среды в объемной стадии длится около 40 с. Избыточная температура на максимуме ~520 °C.
После ~220-й секунды начинается снижение температуры вследствие снижения интенсивности пожара из-за снижения концентрации кислорода. С этого момента теплопотери в конструкции превышают мощность пожара, суммарная тепловая мощность для среды помещения становится отрицательной. Начинается остывание.
Пример 2. Анализ пожара в помещении транспортного въезда.
В расчетных сценариях анализируется горение автомобиля в транспортном въезде в результате розлива и возгорания автомобильного топлива при открытом для погрузочных работ люке в перекрытии между транспортным въездом и вышележащим помещением, которое в свою очередь связано проемами с другими помещениями. Задача исследования – проанализировать распространение тепловых потоков на соседние помещения через открытый люк и проемы; определить максимальные температуры в соседних помещениях и оценить степень опасности пожара на автомобиле для оборудования, находящегося в связанных помещениях. Моделирование пожара ведется с использованием полевой модели.
В расчете предполагается непрерывный пролив и горение топлива и смазочного масла автомобиля в районе двигателя. Площадь горения принята около 4,2 м2. Одновременный пролив большого количества топлива полагается менее опасным вследствие наличия в полу транспортного въезда устройств самотушения проливов легковоспламеняющейся жидкости. При сценарии с пролонгированным проливом топливо и смазочное масло обеспечивают роль высокоэнергетического источника горения и разжигания всех колес автомобиля. При этом колеса создают более высокий уровень пожарной нагрузки, чем само топливо. Начало распространения ОФП при одновременном загорании пролива и передних колес представлено на рис. 10.
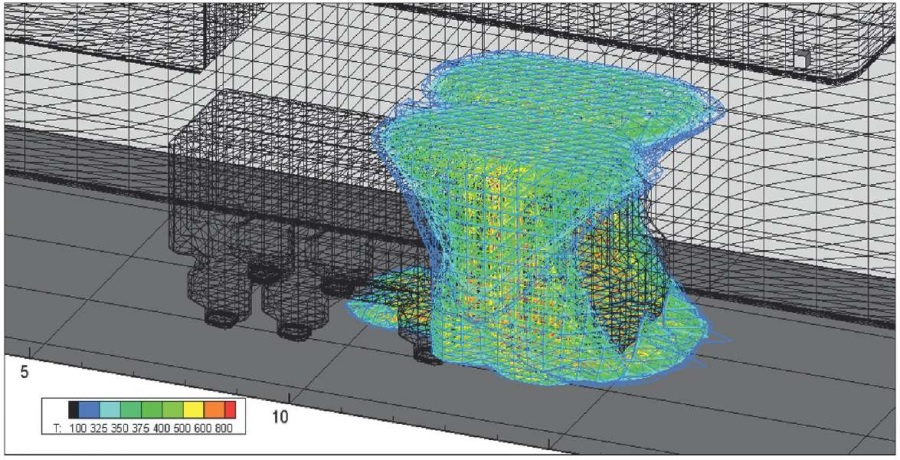
Рис. 10. Поле абсолютной температуры через несколько секунд после начала горения
Fig. 10. Absolute temperature field, few seconds after the outbreak
Расчет пожара проводится для начальных условий: нормальное атмосферное давление, температура окружающей среды – 300 К. Условно, сеткой изолиниями и областями, имеющими температуру менее начальной окружающей среды, выделены конструкции и предметы, исключенные из теплового расчета. На границах данных областей со стороны расчетной области используются термические и газодинамические граничные условия.

Рис. 11. Динамика распространения поля абсолютной температуры, К, через 4 секунды после начала горения всей площади пролива и колес на передней оси
Fig. 11. Absolute temperature field, K, 4 seconds after the onset of burning at the whole spraying area and wheels on front axle

Рис. 12. Динамика распространения поля абсолютной температуры, К, через 5 секунд после начала горения всей площади пролива и колес на передней оси
Fig. 12. Absolute temperature field, K, 5 seconds after the onset of burning at the whole spraying area and wheels on front axle
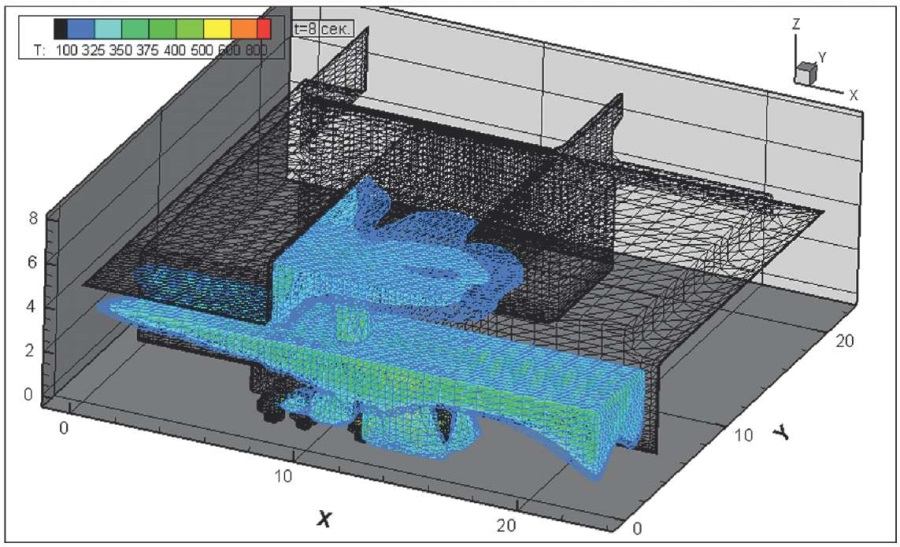
Рис. 13. Динамика распространения поля абсолютной температуры, К, через 8 секунд после начала горения всей площади пролива и колес на передней оси
Fig. 13. Absolute temperature field, K, 8 seconds after the onset of burning at the whole spraying area and wheels on front axle
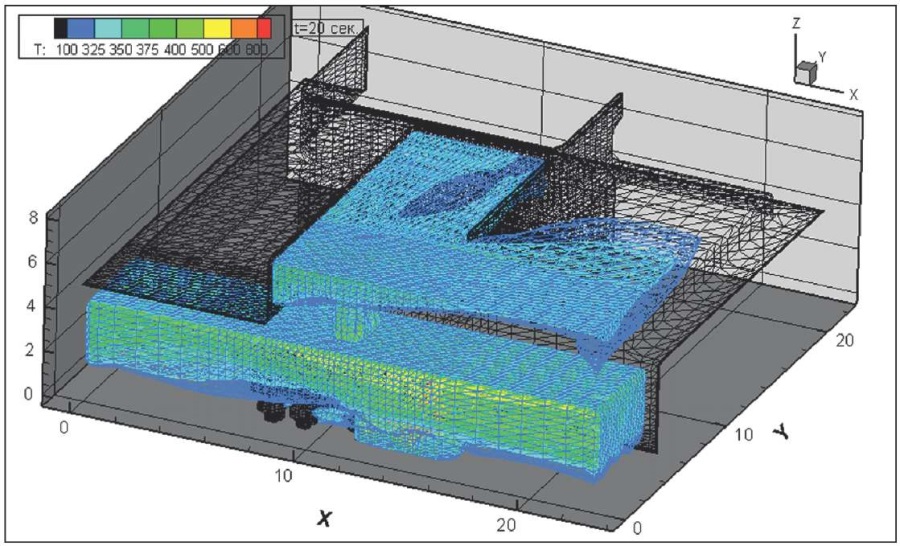
Рис. 14. Динамика распространения поля абсолютной температуры, К, через 20 секунд после начала горения всей площади пролива и колес на передней оси
Fig. 14. Absolute temperature field, K, 20 seconds after the onset of burning at the whole spraying area and wheels on front axle
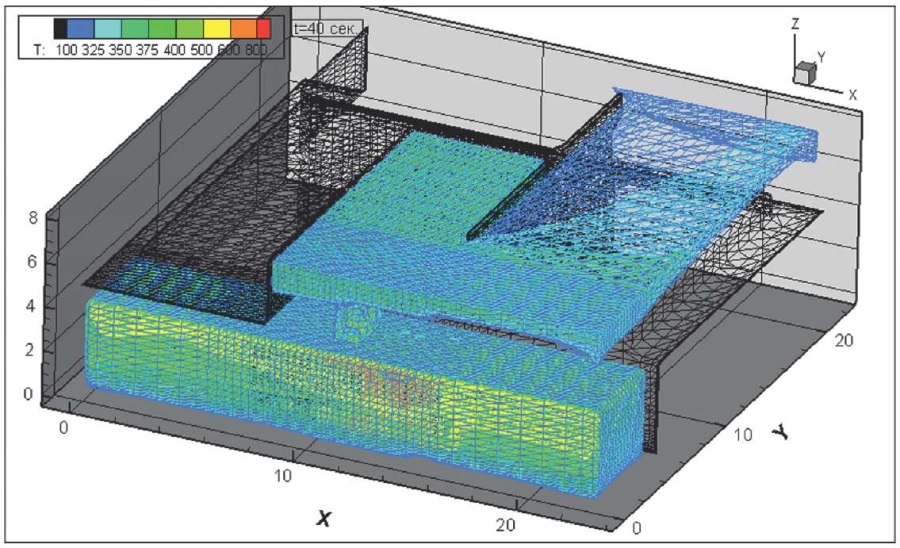
Рис. 15. Динамика распространения поля абсолютной температуры, К, через 40 секунд после начала горения всей площади пролива и колес на передней оси
Fig. 15. Absolute temperature field, K, 40 seconds after the onset of burning at the whole spraying area and wheels on front axle
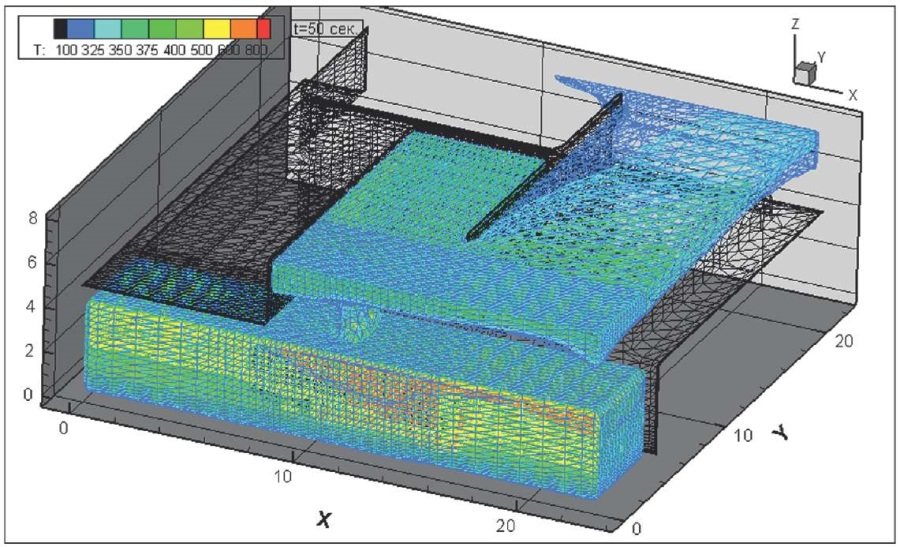
Рис. 16. Динамика распространения поля абсолютной температуры, К, через 50 секунд после начала горения всей площади пролива и колес на передней оси
Fig. 16. Absolute temperature field, K, 50 seconds after the onset of burning at the whole spraying area and wheels on front axle
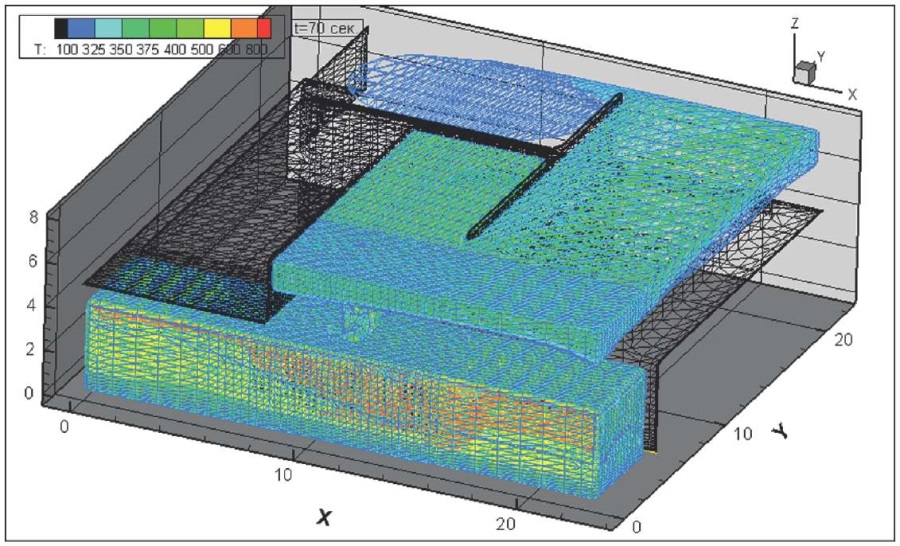
Рис. 17. Динамика распространения поля абсолютной температуры, К, через 70 секунд после начала горения всей площади пролива и колес на передней оси
Fig. 17. Absolute temperature field, K, 70 seconds after the onset of burning at the whole spraying area and wheels on front axle
На рис. 10–17 представлена динамика распространения поля абсолютной температуры, К, через различное время от начала горения всей площади пролива и колес на передней оси.
На рис. 18–25 показана динамика распространения поля абсолютной температуры по сечению здания, К, через 2, 4, 8, 18, 38, 58, 118, 178, 238, 298, 538 с после начала горения всей площади пролива и колес на передней оси.
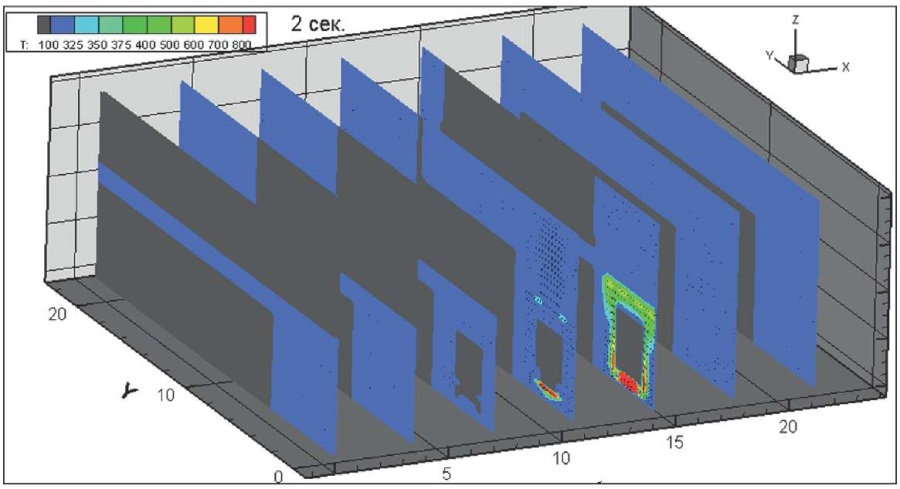
Рис. 18. Динамика распространения поля абсолютной температуры по сечению здания через 2 секунды после начала горения, К
Fig. 18. Absolute temperature field cross section, 2 seconds after the onset of burning, K
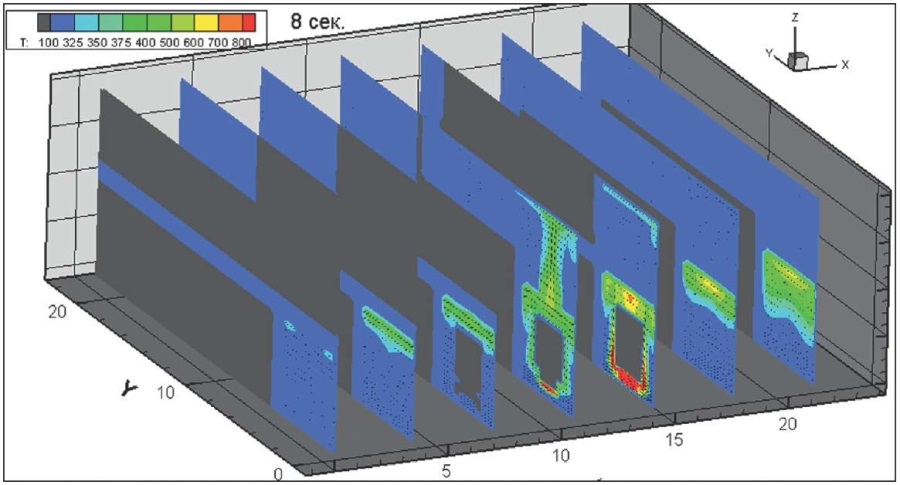
Рис. 19. Динамика распространения поля абсолютной температуры по сечению здания через 8 секунд после начала горения, К
Fig. 19. Absolute temperature field cross section, 8 seconds after the onset of burning, K
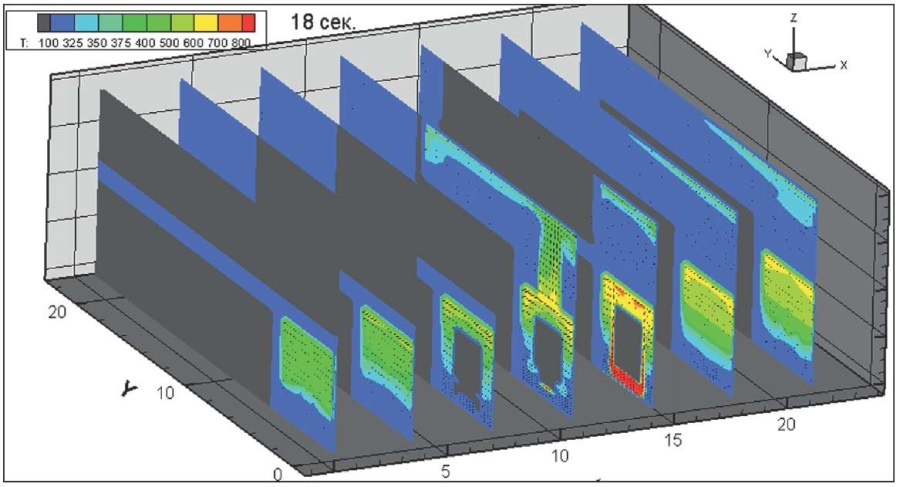
Рис. 20. Динамика распространения поля абсолютной температуры по сечению здания через 18 секунд после начала горения, К
Fig. 20. Absolute temperature field cross section, 18 seconds after the onset of burning, K
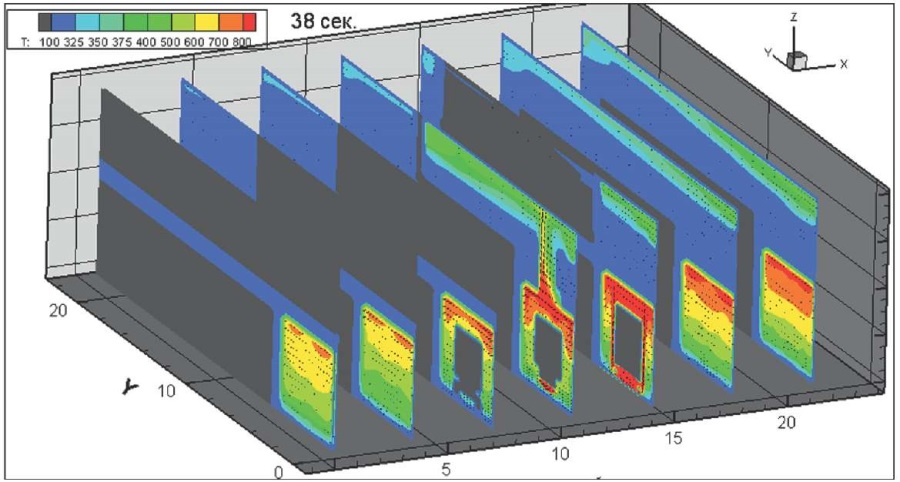
Рис. 21. Динамика распространения поля абсолютной температуры по сечению здания через 38 секунд после начала горения, К
Fig. 21. Absolute temperature field cross section, 38 seconds after the onset of burning, K

Рис. 22. Динамика распространения поля абсолютной температуры по сечению здания через 118 секунд после начала горения, К
Fig. 22. Absolute temperature field cross section, 118 seconds after the onset of burning, K
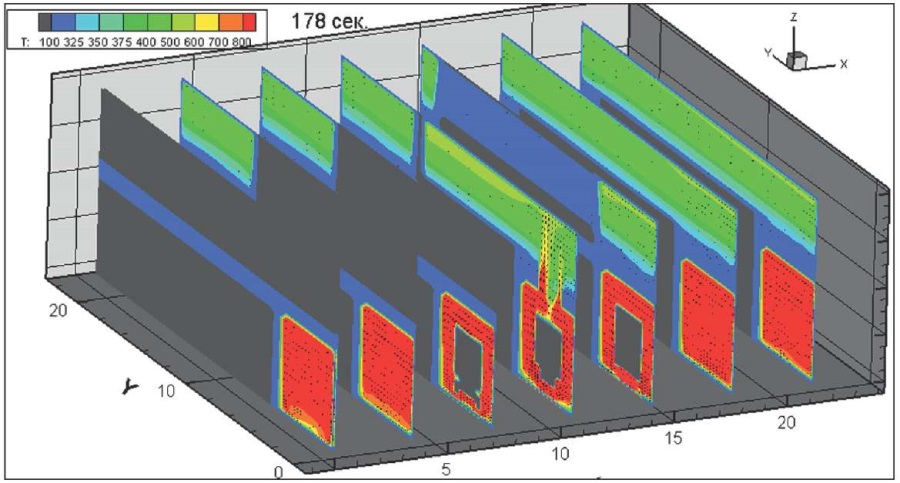
Рис. 23. Динамика распространения поля абсолютной температуры по сечению здания через 178 секунд после начала горения, К
Fig. 23. Absolute temperature field cross section, 178 seconds after the onset of burning, K
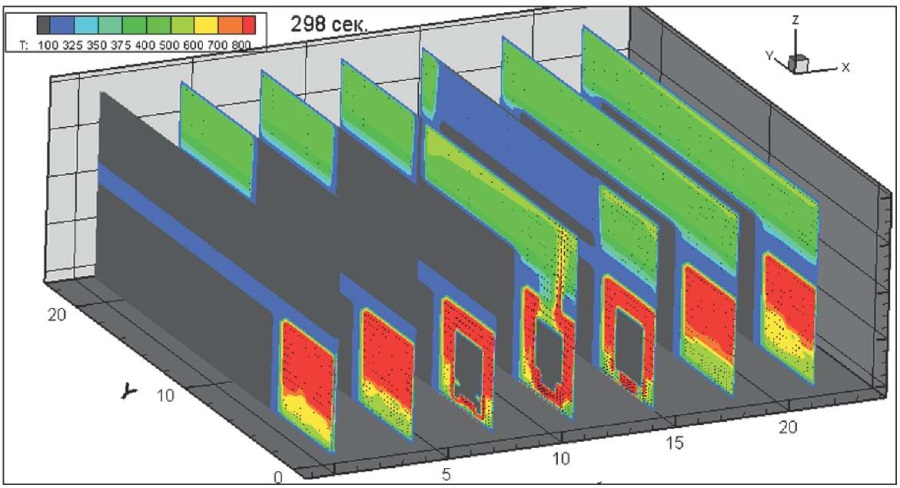
Рис. 24. Динамика распространения поля абсолютной температуры по сечению здания через 298 секунд после начала горения, К
Fig. 24. Absolute temperature field cross section, 298 seconds after the onset of burning, K
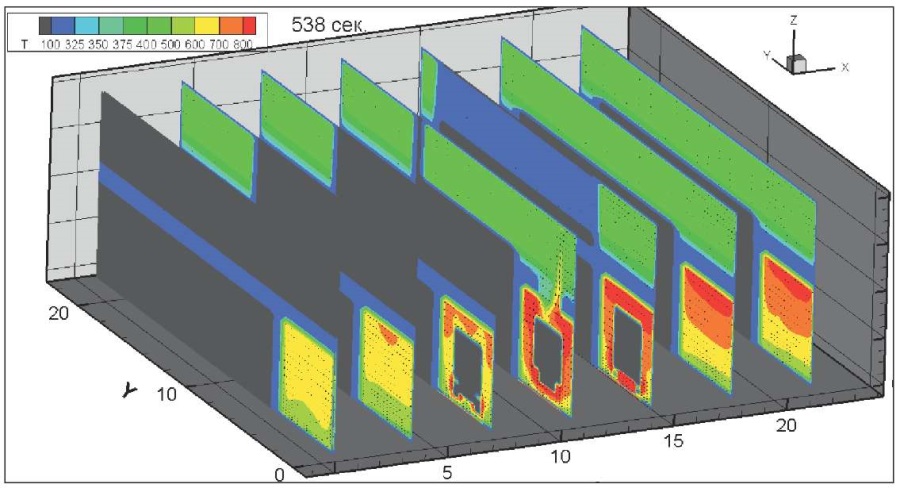
Рис. 25. Динамика распространения поля абсолютной температуры по сечению здания через 538 секунд после начала горения, К
Fig. 25. Absolute temperature field cross section, 538 seconds after the onset of burning, K
Заключение
- Созданная и апробированная полевая модель динамики пожара предназначена для проведения расчетов с учетом специфики пожарной опасности и технологических особенностей атомной станции. Полевая модель динамики пожара оптимизирована с учетом специфики АС, осуществлена ее реализация в рамках комплекса программного обеспечения Fire Dynamics.
- Разработан и верифицирован комплекс программного обеспечения, позволяющий проводить расчеты с использованием полевой модели динамики пожара.
- По мнению авторов статьи, возможно применение полевой модели динамики пожара для проведения расчетов пожара в зданиях и помещениях различного назначения.
- Применение предложенной полевой модели позволяет обосновать достаточность принятых пределов огнестойкости строительных конструкций зданий и помещений, исходя из обеспечения нераспространения пожара за пределы пожарной зоны в течение расчетного времени свободного выгорания всей пожарной нагрузки, в том числе и при углеводородном температурном режиме (при горении углеводородного топлива), например для складов с горюче-смазочными материалами.
Полевой метод является наиболее универсальным из существующих детерминистических методов, поскольку он основан на решении уравнений в частных производных, выражающих фундаментальные законы сохранения в каждой точке расчетной области. С его помощью можно рассчитать температуру, скорость, концентрации компонентов смеси и т. д. в каждой точке расчетной области. В связи с этим полевой метод может широко использоваться для выявления закономерностей развития пожара в помещениях различного назначения.
Список литературы
1. Применение полевого метода математического моделирования пожаров в помещениях: Методические рекомендации. Москва: ВНИИПО; 2003.
2. Пуцев Д.И. Методика анализа влияния пожара на ядерную и радиационную безопасность АЭС [диссертация]. Москва: ВНИИПО; 2001.
3. ГОСТ Р 12.3.047-2012. Система стандартов безопасности труда. Пожарная безопасность технологических процессов. Общие требования. Методы контроля. Москва: Стандартинформ; 2014.
4. Болодьян И.А., Бородкин А.Н., Карпов A.B., Пуцев Д.И. Развитие полевого метода моделирования пожара в помещениях. В: Юбилейный сборник трудов ФГУ ВНИИПО МЧС России. Москва: ВНИИПО; 2007, с. 54–121.
5. Верификация трехмерной математической модели расчета динамики пожара для оценки воздействие пожара на оборудование АЭС. Москва: ООО «СТЭМ»; 2001. Арх. № Ф-17204, № Ф-17409, № Ф-17486.
6. РД 03-34-2000. Требования к составу и содержанию отчета о верификации и обосновании программных средств, применяемых для обоснования безопасности объектов использования атомной энергии [интернет]. Режим доступа: https://www.secnrs.ru/upload/files/rd2000.pdf
7. РД 03-33-2008. Инструкция об организации проведения экспертизы программных средств, применяемых при обосновании и (или) обеспечении безопасности объектов использования атомной энергии [интернет]. Режим доступа: https://gostrf.com/normadata/1/4293832/4293832652.pdf
8. Пуцев Д.И. Методы, рекомендуемые для дальнейшего анализа пожарной безопасности 4-го энергоблока Кольской АЭС. Краткая характеристика и некоторые результаты применения расчетных методов. В: Методы пожарной опасности российских АЭС. Материалы международного семинара. Москва: ВНИИАЭС; 2000.
9. Исследования развития пожаров в помещениях АЭС с целью определения прогрева строительных конструкций в условиях пожара. Отчет о научно-исследовательской работе. Москва: ВНИИПО; 1985.
10. Провести исследования и разработать рекомендации по повышению устойчивости функционирования управляющих систем защиты ядерных реакторов АСТ от воздействия опасных факторов пожара. Отчет о НИР. Москва: ВНИИПО; 1989.
11. Молчадский И.С., Бородкин А.Н. Тепловыделение при пожарах в помещениях. Пожаровзрывобезопасность. 1992;1(1):41–45.
12. Борисов В.Н., Пуцев Д.И., Угорелов В.А. Общие требования к противопожарной защите атомных станций. В: Проблемы горения и тушения на рубеже веков. Материалы XV научно-практической конференции. Москва: ВНИИПО; 1999.
13. Борисов В.Н., Пуцев Д.И., Угорелов В.А. Методика оценки теплового воздействия пожара на оборудование АЭС. В: Проблемы горения и тушения на рубеже веков. Материалы XV научно-практической конференции. Москва: ВНИИПО; 1999.
14. Глухов И.С., Пуцев Д.И. Результаты предварительного зонирования 4-го энергоблока Кольской АЭС. В: Методы пожарной опасности российских АЭС. Материалы международного семинара. Москва: ВНИИАЭС; 2000.
15. Кошмаров Ю.А., Пузач С.В., Андреев В.В., Козлов Ю.И. Прогнозирование опасных факторов пожара в помещении. Москва: Академия ГПС МЧС России; 2012.
16. Лобанова H.A., Пуцев Д.И., Томилин A.B., Хасанов И.Р. Обеспечение пожарной безопасности энергоблоков АЭС нового поколения. В: Актуальные проблемы пожарной безопасности: XXI международная научно-практическая конференция. Тезисы докладов – 4.1. Москва: ФГУ ВНИИПО МЧС России; 2009, с. 105–108.
17. Хасанов И.Р., Голованов В.И. Развитие методов исследования огнестойкости и пожарной опасности строительных конструкций и инженерного оборудованияю. В: Юбилейный сборник трудов ФГУ ВНИИПО МЧС России. Москва: ВНИИПО; 2007, с. 121–158.
18. Болодьян И.А., Нигоренко Н.В., Пуцев Д.И., Терехов И.В. Анализ безопасности энергоблока с реактором ВВЭР-440 при возникновении пожара в машинном зале и кабельных помещениях систем расхолаживания реакторной установки. В: Снижение риска гибели людей при пожарах. Материалы XVIII Науч.-практ. конф. Москва: ВНИИПО; 2003.
19. Борисов В.Н., Пуцев Д.И., Томилин A.B. Методика вероятностного анализа безопасности АЭС при пожаре. В: Актуальные проблемы пожарной безопасности: XXI международная научно-практическая конференция. Тезисы докладов – 4.1. Москва: ФГУ ВНИИПО МЧС России; 2009, с. 108–111.
20. Борисов В.Н., Пуцев Д.И., Томилин А.В. Методика определения пожарных зон, влияющих на безопасность. В: Актуальные проблемы пожарной безопасности. Материалы XXII международной научно-практической конференции. Москва: ВНИИПО; 2010. с. 32–38.
21. Борисов В.Н., Пуцев Д.И., Томилин А.В. Определение частоты возникновения пожара в выбранных пожарных зонах АЭС. В: Актуальные проблемы пожарной безопасности. Материалы XXII международной научно-практической конференции. Москва: ВНИИПО; 2010. с. 279–283.
22. Пуцев Д.И. Специальные требования пожарной безопасности для атомных станций. Пожарная безопасность. 2010;(3):138–140.
23. Дешевых Ю.И., Гилетич А.Н., Комков П.М., Пуцев Д.И., Томилин A.B. Развитие системы нормирования пожарной безопасности атомных станций. Пожарная безопасность. 2011;(3):66–70.
24. СП 13.13130.2009. Атомные станции. Требования пожарной безопасности. Москва: ФГУ ВНИИПО МЧС России; 2009.
25. Рекомендации по оценке пожароуязвимости систем (элементов), важных для безопасности, на Российских АЭС. Москва: ВНИИАЭС; 2000.
26. Ingberg S.H. Tests of the Severity of Building Fires. NFPA Quarterly. 1928;22(1):43–61.
27. Молчадский И.С. Приведение температурного режима пожара к стандартному. В: Огнестойкость строительных конструкций: сб. тр. Москва: ВНИИПО; 1979, Вып. 7, с. 3–7.
28. Молчадский И.С., Зотов С.В. Расчет требуемого предела огнестойкости и допустимой пожарной нагрузки железобетонных колонн. В: Огнестойкость строительных конструкций: сб. научных трудов. Москва: ВНИИПО; 1984, с. 50–65.
29. Алексашенко А.В., Кошмаров Ю.А., Молчадский И.С. Тепломассоперенос при пожаре. Москва: Стройиздат; 1982.
30. Методы расчета температурного режима пожара в помещениях зданий различного назначения. Рекомендации. Москва: ВНИИПО; 1988.
31. Болодьян А.А., Глухов И.С., Пуцев Д.И. Математическое моделирование переноса газо-аэрозольных смесей в объеме помещения. В: Научно-техническое обеспечение противопожарных и аварийно-спасательных работ. Материалы XII научно-практической конференции. Москва: ВНИИПО; 1993, с. 164–165.
32. Борисов В.Н., Пуцев Д.И., Угорелов В.А. Методика оценки теплового воздействия пожара на оборудование АЭС. В: Проблемы горения и тушения пожаров на рубеже веков. Материалы XV научно-практической конференции. Москва: ВНИИПО; 1999.
33. Карпов А.В., Рыжов А.М. Рекомендации по применению полевого метода математического моделирования пожара. Москва: ВНИИПО; 2002.
34. Руководство по расчету температурного режима пожара в помещениях жилых зданий. Москва: ВНИИПО; 1983.
35. Гутов В.Н. Зонная математическая модель развитой стадии пожара. В: Безопасность людей при пожарах в зданиях и сооружениях: сб. науч. трудов. Москва: ВНИИПО МВД СССР; 1987, с. 62–69.
36. Гутов В.Н., Лицкевич В.В. Математическая модель пламенного горения в здании. Пожаровзры вобезопасность. 1994;3(4):58–65.
37. Молчадский И.С., Астахова И.Ф. Математическая модель температурных полей начальной стадии пожара в помещении. Пожаровзрывобезопасность. 1995;4(2):31–33.
38. Молчадский И.С., Зернов С.И. Определение продолжительности начальной стадии пожара. В: Пожарная профилактика: сб. научных трудов. Москва: ВНИИПО; 1981, с. 26–45.
39. Зотов С.В. Эквивалентная продолжительность пожара для железобетонных конструкций в зданиях химических производств [диссертация]. Москва; 1991.
Об авторах
Д. И. ПуцевРоссия
Дмитрий Игоревич Пуцев, д-р техн. наук, генеральный директор
ул. Свердлова, д. 65, офис 5, г. Балашиха, 143900
Ю. В. Кривцов
Россия
Юрий Владимирович Кривцов, д-р техн. наук, руководитель научного экспертного бюро пожарной, экологической безопасности в строительстве
2-я Институтская ул., д. 6, к. 1, г. Москва, 109428
Ю. М. Грошев
Россия
Юрий Михайлович Грошев, канд. техн. наук, ведущий специалист научного экспертного бюро пожарной, экологической безопасности в строительстве
2-я Институтская ул., д. 6, к. 1, г. Москва, 109428
Н. А. Лобанова
Россия
Нина Александровна Лобанова, канд. техн. наук, главный специалист
ул. 2-я Советская, д. 9/2 а, г. Санкт-Петербург, 191036
Рецензия
Для цитирования:
Пуцев Д.И., Кривцов Ю.В., Грошев Ю.М., Лобанова Н.А. Оценка возможности применения полевого моделирования пожара для проведения расчетов пожаров в зданиях и помещениях. Вестник НИЦ «Строительство». 2023;37(2):37-70. https://doi.org/10.37538/2224-9494-2023-2(37)-37-70. EDN: ETZDYW
For citation:
Putsev D.I., Krivtsov Yu.V., Groshev Yu.M., Lobanova N.A. Evaluating feasibility of field modeling of fire to calculate fire characteristics in buildings and premises. Bulletin of Science and Research Center of Construction. 2023;37(2):37-70. (In Russ.) https://doi.org/10.37538/2224-9494-2023-2(37)-37-70. EDN: ETZDYW


























