Перейти к:
Некоторые соображения о построении современной теории расчета железобетонных конструкций (продолжение)
https://doi.org/10.37538/2224-9494-2023-3(38)-37-45
EDN: JOAGTR
Аннотация
Введение. Статья развивает результаты исследования, опубликованного авторами ранее, применив их для построения нелинейной диссипативной теории силового сопротивления бетона сжатию. Авторами статьи решается важная и актуальная задача, направленная на совершенствование теории расчета бетонных и железобетонных конструкций с учетом накопленных к настоящему моменту знаний.
Цель. Показать возможный путь построения нелинейной диссипативной теории силового сопротивления бетона сжатию в условиях отсутствия нормативных режимов нагружения, используя вместо них нормативную классификацию нагрузок.
Результаты. Уравнение состояния теории упруго-ползучего тела, наиболее точной из существующих на сегодня, но и наиболее трудоемкой в практическом использовании, без потери ее положительных свойств, сведено по форме к уравнению нестареющего бетона с его простотой в применении. При этом уравнение состояния бетона в практически важных случаях разрешается в элементарных функциях и замкнутом виде.
Подавляющее большинство известных в научной литературе о железобетоне сведений о характере кривых ползучести в области надежной работы конструкций свидетельствует об их гладкости и непрерывности. Это дает основание для распространения данных, полученных при кратковременных испытаниях, на весь временной интервал, открывая возможность экспресс-анализа дерформативных свойств бетона.
Приведена оценка обратимости деформаций ползучести. Обнаружена диссипативность упругих деформаций. Построена нелинейная связь деформации с постоянным уровнем напряжения, на основе которой показан возможный путь построения нелинейной диссипативной теории силового сопротивления бетона сжатию в условиях отсутствия нормирования режимов нагружения, используя вместо них нормативную классификацию нагрузок.
Выводы. В заключение отмечается, что рассмотренные экспериментальные данные в связи с их малочисленностью дают качественную информацию. Количественную оценку можно получить, проведя необходимое количество воспроизведений опытов.
Ключевые слова
Для цитирования:
Назаренко В.Г., Звездов А.И., Ларионов Е.А. Некоторые соображения о построении современной теории расчета железобетонных конструкций (продолжение). Вестник НИЦ «Строительство». 2023;38(3):37-45. https://doi.org/10.37538/2224-9494-2023-3(38)-37-45. EDN: JOAGTR
For citation:
Nazarenko V.G., Zvezdov A.I., Larionov E.A. Calculation of reinforced concrete structures: considerations on developing new theory (continued). Bulletin of Science and Research Center of Construction. 2023;38(3):37-45. (In Russ.) https://doi.org/10.37538/2224-9494-2023-3(38)-37-45. EDN: JOAGTR
В линейной постановке зависимость деформации от уровня напряжений сжатия при простейшем нагружении призмы [1]:
ε(t, τ) = η(τ)εR[ 1 + φf (t − τ)], (1)
где f(t − τ) = 1 − ke−γ(t − τ) – функция накопления деформаций;
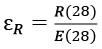 – предельная сжимаемость бетона в возрасте 28 суток.
– предельная сжимаемость бетона в возрасте 28 суток.
Принятая запись функции накопления деформаций ползучести в момент нагружения определяет восходящий участок прямой графика меры ползучести, который реализуется за несопоставимо короткий отрезок времени по сравнению со временем эксплуатации конструкции, когда проявляется сама ползучесть. Этот участок сейчас относят к ползучести и называют ее быстронатекающей, отнеся ее к необратимым деформациям. Е. Н. Щербаков называл меру ползучести мерой в начальных отрезках.
Эволюция деформаций определяется дифференциальным соотношением
dε(t,τ) = dη(τ)εR[ 1 + φf(t − τ)], (2)
которое является ОДУ первого порядка, решая которое прямым интегрированием, получаем уравнение для деформаций в зависимости от изменения уровня напряжений во времени
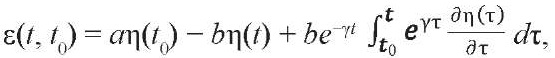 (3)
(3)
где a = εR(1 + φ) и b = εRkφ. Если взять интеграл по частям, то получим
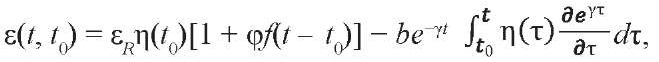 (3а)
(3а)
Обычно в научной литературе это уравнение называют уравнением механического состояния. Решая (2) относительно уровней напряжения, получаем уравнение релаксации
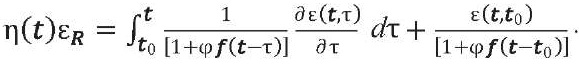 (4)
(4)
Таким образом, уравнение состояния теории упруго-ползучего тела, наиболее точной из существующих на сегодня, но и наиболее трудоемкой в практическом использовании, без потери ее положительных свойств, сведено по форме к уравнению нестареющего бетона (3) с его простотой в практическом применении. Уравнения (3), (4) в практически важных случаях разрешаются в элементарных функциях и замкнутом виде.
Последние опытные данные, полученные в НИИЖБ им. А. А. Гвоздева Е. Н. Паньковым при уровне напряжений, в соответствии с ГОСТ 24452 [2] и ГОСТ 24544 [3], равном 0,33 показывают, что упругие деформации наряду с известным свойством нелинейности [1] рассеивают энергию. Это отчетливо видно на рис. 1. График (рис. 1) построен для начального нагружения призмы за 30 секунд до уровня 0,33 от ее прочности, выдержки на этом уровне 24 минуты и сбросе всей нагрузки в течение 22 секунд.
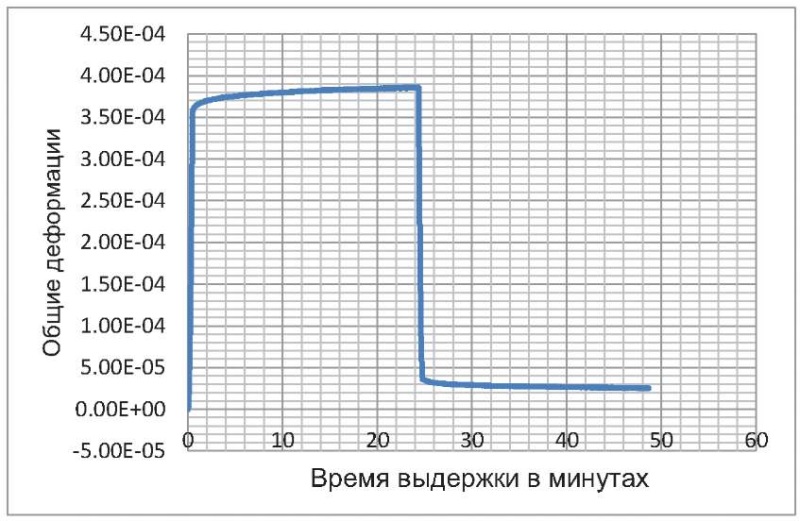
Рис. 1. Развитие деформаций в уровнях 0–0,33–0
Fig. 1. Development of strain at 0–0, 33–0
На графике (рис. 2) отдельно показано развитие упругих деформаций, из которого видно, что в интервале времени 14–58 секунд упругие деформации симметричны относительно максимума, что свидетельствует об их обратимости на этом интервале.
Вне его они необратимы. Коэффициент необратимости равен 4Е-05/3.6Е-04 = 0,11.
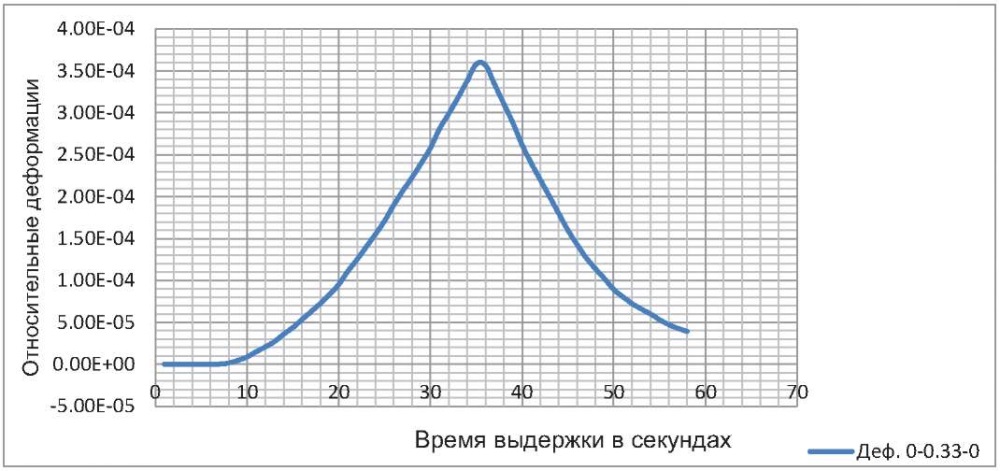
Рис. 2. Развитие упругих деформаций
Fig. 2. Development of elastic strain
Рассеивают энергию и деформации ползучести. Это также известный факт. Вопрос только в ее количестве. Если в существующих теориях оно оценивается около 20 %, то, по данным Е. Н. Панькова, составляет больше половины (см. следующие графики – рис. 3, 4).
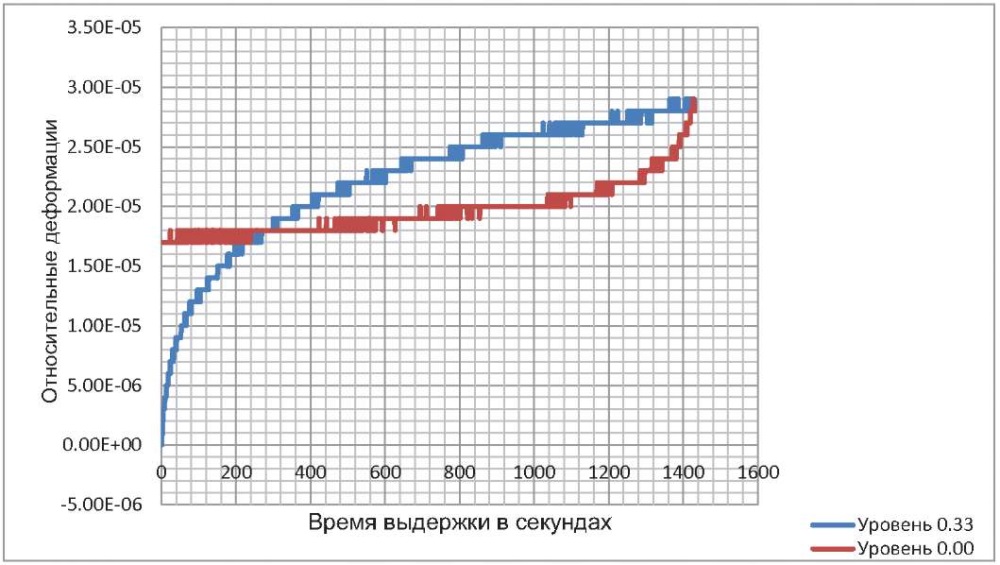
Рис. 3. Ползучесть на уровнях 0,33–0
Fig. 3. Creep at 0.33–0
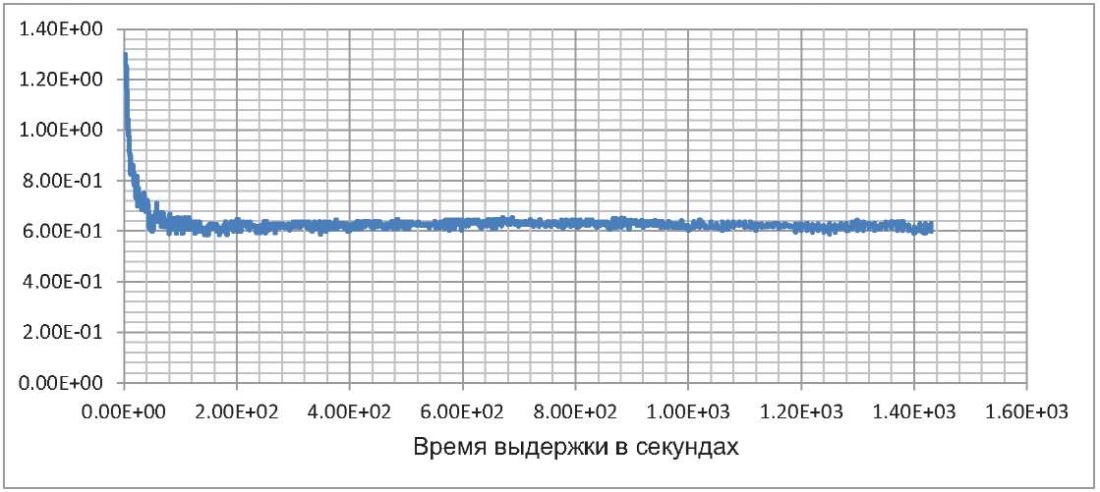
Рис. 4. Коэффициент необратимости деформаций ползучести
на уровне напряжения 0,33
Fig. 4. Irreversibility coefficient of creep strain at 0.33 stress
График на рис. 4 показывает, что коэффициент необратимости постоянен во времени. Это свидетельствует об аффинноподобии кривых мер полных, обратимых и необратимых деформаций. А это, в свою очередь, «приводит к весьма важному в практическом отношении следствию о возможности инвариантного учета основных факторов, влияющих на изменение частных деформаций» [4]. Из сопоставления графиков видно, что в рассматриваемом опыте необратимость упругих деформаций почти в пять раз меньше необратимости деформаций ползучести.
Подавляющее большинство известных в научной литературе о железобетоне сведений о характере кривых ползучести в области надежной работы конструкций свидетельствуют об их гладкости и непрерывности. Это дает основание для распространения данных, полученных при кратковременных испытаниях, на весь временной интервал, открывая возможность экспресс-анализа дерформативных свойств бетона.
В заключение этой части отмечаем, что рассмотренный эксперимент дает качественную информацию. Количественную оценку можно получить, проведя необходимое количество воспроизведений опыта.
При построении нелинейной теории следует всего лишь в (1) уровень напряжения η(τ) помножить на функцию нелинейности. В связи с этим приводим цитату В. М. Бондаренко: «В литературе приводится множество различных записей для функции нелинейности; каждый раз введение новых предложений мотивируется какими-нибудь локальными причинами; среди них обычно фигурируют соображения точности аппроксимации экспериментальных данных, хотя чаще всего достоверность ожидаемой точности не доказывается» [5]. Анализ этих предложений выявил предпочтительные, которые в итоге и были заложены в «Рекомендации по учету ползучести и усадки бетона при расчете бетонных и железобетонных конструкций. НИИЖБ, 1988» [6]. С учетом результатов [7–9], принимая усредненную функцию нелинейности,
S 0(η(τ)) = [ 1 + v(η(τ))m], (5)
получим нелинейную связь деформации при постоянном уровне напряжения
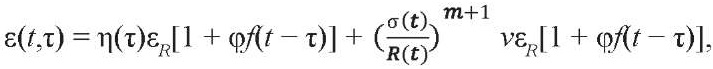 (6)
(6)
где φ = E(28)С(∞,28);
v и m – параметры нелинейности.
Первое слагаемое в (6) представляет величину обратимых (потенциальных) деформаций, второе выражает величину необратимых омертвленных (диссипативных) деформаций, которые накапливаются достаточно быстро. По данным К. З. Галустова – за 40–50 суток, по данным В. В. Соломонова – за 5 суток. Предпосылка о том, что нелинейная часть (6) необратима, признается в научной литературе, однако в [7][10] полагается, что она необратима частично, в [11] – необратима полностью, в [12] утверждается, что [7][10][11] не дают строгого аналитического решения уравнения при отыскании необратимой деформации и неприемлемы при решении релаксационной задачи. Заметим, что собственные публикации, на которые ссылается [12], заканчиваются в 1986 году.
Позднее А. А. Котов, опираясь на исследования В. Д. Харлаба (1981, 1983, 1996 гг.), фактически принимая основной принцип двухкомпонентной теории ползучести, говорит: «Естественным с физической точки зрения выглядит изначальное разделение процессов ползучести на обратимые и необратимые. Отсюда начальный постулат о структуре деформации ползучести предлагается формулировать так: полная деформация складывается из мгновенно упругой и деформаций, развивающихся во времени: полностью обратимой и полностью необратимой. Обратимая деформация является результатом вязкого течения материала, происходящего без нарушения структурных связей, определяющих потенциальную прочность материала, и поэтому обратима. Необратимая деформация отражает процесс постепенного разрушения этих связей под воздействием напряжений и поэтому необратима. Обратимая деформация ползучести не может быть ничем иным, как наследственно упругой деформацией, соответствующей принципу суперпозиции Больцмана – Вольтерра (обратимость гарантируется наследственной упругостью, а наследственная упругость предполагает линейность» [8].
Из этого непосредственно следует, что необратимые деформации равны разности общих и линейной частей деформаций, а это и есть нелинейная часть деформаций согласно (6). Приведенный выше обзор исследований показывает необходимость дополнительной экспериментальной проверки. Согласно [12], величина необратимых деформаций определяется максимальным уровнем напряжения с учетом всех сочетаний нагрузок в интервале τ, t. Уравнение (6) позволяет способом, используемым в линейной постановке, построить уравнения деформаций и релаксации при переменном уровне напряжений или вынужденных деформаций.
За исследованиями этого направления можно обратиться к [9] и там увидеть, что потребуется иметь режимы нагружений, которых, как известно, великое множество и которые не содержатся пока в действующих нормах. Как говорил Д. Пойа: «Пока никто не достиг Полярной звезды, но многие, глядя на нее, находили правильный путь». Один из путей можно найти, если интегрирование заменить простой суммой. Число членов в той сумме невелико. Согласно действующим нормам, в большинстве случаев нагрузки делятся на постоянные, временные длительные и временные кратковременные. Поэтому в функции f(t − τ) = 1 − ke −γ(t − τ) для обратимых деформаций аргумент можно принять равным бесконечности для первых и вторых видов нагрузок, нулю – для третьего вида и для необратимой части деформаций.
Список литературы
1. <i>Назаренко В.Г., Звездов А.И., Ларионов Е.А.</i> Некоторые соображения о построении современной теории расчета железобетонных конструкций. Вестник НИЦ «Строительство». 2022;35(4):80–87. https://doi.org/10.37538/2224-9494-2022-4(35)-80-87
2. ГОСТ 24452-80. Бетоны. Методы определения призменной прочности, модуля упругости и коэффициента Пуассона. Москва: Стандартинформ; 2005.
3. ГОСТ 24544-81. Бетоны. Методы определения деформаций усадки и ползучести [интернет]. Режим доступа: https://gostrf.com/normadata/1/4294853/4294853100.pdf ГОСТ отменен. Новый: ГОСТ 24544-2020 https://gostassistent.ru/doc/11cdb233-16b3-42f5-a5a2-eb600f3edcf7
4. <i>Бондаренко В.М., Бондаренко С.В.</i> Инженерные методы нелинейной теории железобетона. Москва: Стройиздат; 1982.
5. <i>Бондаренко В.М</i>. Диалектика механики железобетона. Бетон и железобетон. 2002;(1):24–27.
6. НИИЖБ Госстроя СССР. Рекомендации по учету ползучести и усадки бетона при расчете бетонных и железобетонных конструкций. Москва: Стройиздат; 1988. 120 с.
7. <i>Александровский С.В., Попкова О.М</i>. Исследование нелинейных деформаций бетона молодого возраста при ступенчато изменяющихся напряжениях сжатия. В: Ползучесть и усадка бетона. Материалы Совещания, Киев, 1969 г. Москва: Стройиздат; 1969, с. 30–52.
8. <i>Котов А.А</i>. К теории ползучести и длительной прочности бетона. Вестник МГТУ. Труды Мурманского государственного технического университета. 2002;5(2):161–166.
9. <i>Барашиков А.Я</i>. Исследование длительной работы железобетонных конструкций при переменных нагрузках [диссертация]. Киев; 1978.
10. <i>Колесников Н.А.</i> Исследование нелинейной ползучести и релаксации напряжений в бетоне при повторных воздействиях напряжений или деформаций сжатия [диссертация]. Москва; 1970.
11. <i>Соломонов В.В.</i> Исследование предшествующего процесса деформирования на линейные и нелинейные деформации ползучести бетона при постоянных и переменных напряжениях сжатия [диссертация]. Москва; 1973.
12. <i>Галустов К.З</i>. Нелинейная теория ползучести бетона и расчет железобетонных конструкций. Москва: Физматлит; 2006.
13. <i>Назаренко В.Г</i>. Развитие основ теории расчета железобетонных конструкций с учетом особенностей режимного нагружения [диссертация]. Москва; 1990.
14. <i>Бондаренко С.В., Назаренко В.Г.</i> Методика теории ползучести. Москва: ВЗИСИ; 1981.
Об авторах
В. Г. НазаренкоРоссия
Виталий Григорьевич Назаренко, д-р техн. наук, профессор
А. И. Звездов
Россия
Андрей Иванович Звездов, д-р техн. наук, профессор, заместитель генерального директора по научной работе
e-mail.: zvezdov@list.ru
Е. А. Ларионов
Россия
Евгений Алексеевич Ларионов, д-р техн. наук, профессор
Рецензия
Для цитирования:
Назаренко В.Г., Звездов А.И., Ларионов Е.А. Некоторые соображения о построении современной теории расчета железобетонных конструкций (продолжение). Вестник НИЦ «Строительство». 2023;38(3):37-45. https://doi.org/10.37538/2224-9494-2023-3(38)-37-45. EDN: JOAGTR
For citation:
Nazarenko V.G., Zvezdov A.I., Larionov E.A. Calculation of reinforced concrete structures: considerations on developing new theory (continued). Bulletin of Science and Research Center of Construction. 2023;38(3):37-45. (In Russ.) https://doi.org/10.37538/2224-9494-2023-3(38)-37-45. EDN: JOAGTR


























