Перейти к:
Численное моделирование сейсмоизолированных зданий с фрикционно-маятниковыми опорами
https://doi.org/10.37538/2224-9494-2023-3(38)-143-154
EDN: YGFQNY
Аннотация
Введение. В настоящее время на территории Таджикистана проектируются и возводятся здания и сооружения на основе пассивных способов обеспечения сейсмостойкости, что в итоге приводит к увеличению жесткости и веса сооружений и, соответственно, увеличению сейсмической нагрузки. В статье рассматривается решение задачи, связанной с сейсмоизоляцией зданий с применением фрикционно-маятниковых опор. Динамическая модель исследуемого объекта представлена в виде системы, состоящей из суперструктуры, субструктуры и сейсмоизоляции.
Целью работы является дальнейшее развитие методов анализа и оценки параметров систем сейсмоизоляции и сейсмозащиты зданий и сооружений для обоснования условий эффективности их применения в сейсмостойком строительстве на территории Республики Таджикистан.
Материалы и методы. Использованы методы строительной механики, динамики сооружений, а также методы численного моделирования. Методика исследований включала построение математических моделей рассматриваемых систем, их численный анализ, сопоставление полученных результатов с имеющимися данными. Проводились экспериментальные исследования на модели фрагмента здания с использованием виброплатформы.
Результаты. Разработана математическая модель, позволяющая проводить исследования напряженно-деформированного состояния здания с маятниковыми скользящими опорами при различных внешних воздействиях, в том числе сейсмических. Система дифференциальных уравнений с использованием метода последовательных аппроксимаций преобразуется в систему алгебраических уравнений, которая решается на каждом шаге по времени. На основе разработанного алгоритма составлена компьютерная программа на языке Fortran и получены результаты численного решения динамической задачи по расчету многоэтажного здания с маятниковыми скользящими опорами. На примере 10-этажного каркасного здания получены результаты от действия мгновенного импульса.
Выводы. Сравнение результатов показывает, что применение сейсмоизоляции в виде фрикционно-маятниковых опор приводит к значительному уменьшению внутренних усилий в опорной части, а также к уменьшению скорости и ускорения в верхней части здания по сравнению с моделью без сейсмоизолирующих опор. При этом несколько увеличиваются перемещения как в нижней, так и верхней частях исследуемого объекта.
Ключевые слова
Для цитирования:
Низомов Д.Н., Сангинов А.М. Численное моделирование сейсмоизолированных зданий с фрикционно-маятниковыми опорами. Вестник НИЦ «Строительство». 2023;38(3):143-154. https://doi.org/10.37538/2224-9494-2023-3(38)-143-154. EDN: YGFQNY
For citation:
Nizomov D.N., Sanginov A.M. Numerical simulation of seismically isolated buildings with friction pendulum bearings. Bulletin of Science and Research Center of Construction. 2023;38(3):143-154. (In Russ.) https://doi.org/10.37538/2224-9494-2023-3(38)-143-154. EDN: YGFQNY
Фрикционно-маятниковые опоры (ФМО) (или маятниковые скользящие опоры) в зависимости от конструктивных решений подразделяются на опоры: с одной сферической поверхностью скольжения – одномаятниковые скользящие опоры; с двумя сферическими поверхностями скольжения – двухмаятниковые скользящие опоры; с четырьмя сферическими поверхностями скольжения – трехмаятниковые скользящие опоры. Фрикционные опоры называются маятниковыми скользящими, так как расположенная на них конструкция совершает колебания, подобные движениям математического маятника при наличии трения. Маятниковые опоры изготавливают из нержавеющей стали, а их сферические поверхности имеют покрытия из материалов, обладающих заданными фрикционными свойствами [1–3]. Вопросы численного решения динамических задач и сейсмозащиты рассмотрены в работах [4–11].
Рассмотрим многоэтажное здание с сейсмоизоляцией при сейсмическом воздействии. В качестве сейсмозоляции используются маятниковые скользящие опоры. Динамическая модель исследуемого объекта, которая состоит из n сосредоточенных масс, представлена на рис. 1а. Одномаятниковая скользящая опора состоит из двух горизонтальных плит, одна из которых имеет сферическую вогнутую поверхность и расположена между плитами сферического шарнирного ползуна (рис. 2а). Особенности поведения и сейсмоизолирующие свойства одномаятниковой скользящей опоры зависят от радиуса кривизны сферической поверхности R и значения коэффициента трения скольжения μ ползуна по сферической поверхности (рис. 2б). Как следует из статического равновесия сил, действующих и возникающих в процессе скольжения по сферической поверхности,
F = FTcosα + FN sinα, (1)
Q = FNcosα – FT sinα, (2)
sinα = u1/R, cosα = (R – δ)/R = 1 – δ/R,
где F, Q – горизонтальная и вертикальная силы, действующие на фрикционную опору;
FT , FN – тангенциальная и нормальная силы, действующие на ползунок скольжения;
R – радиус сферической поверхности.
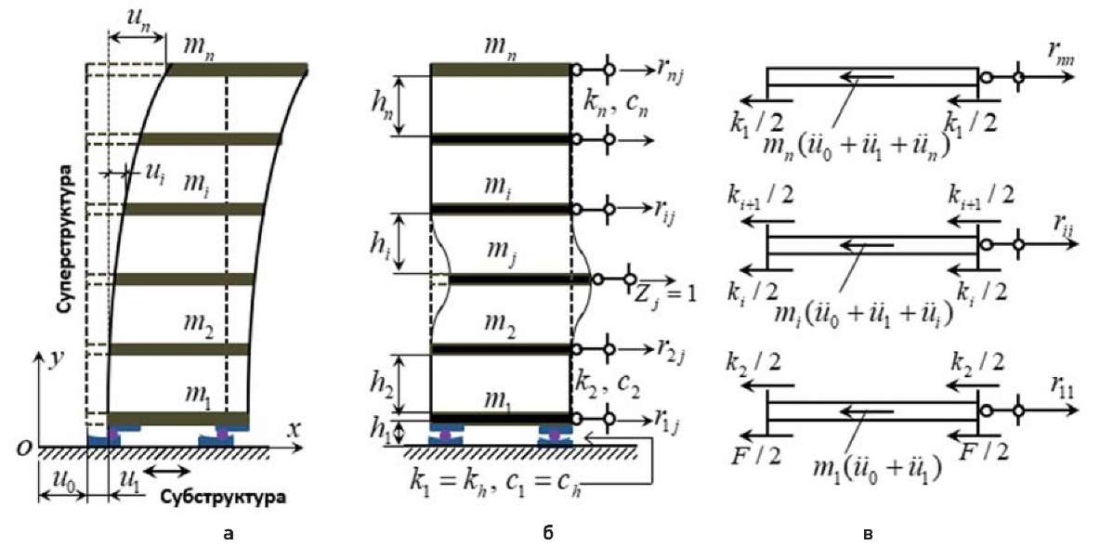
Рис. 1. Динамическая модель здания и основная система метода перемещений
Fig. 1. Dynamic building model and basic system of deflection method
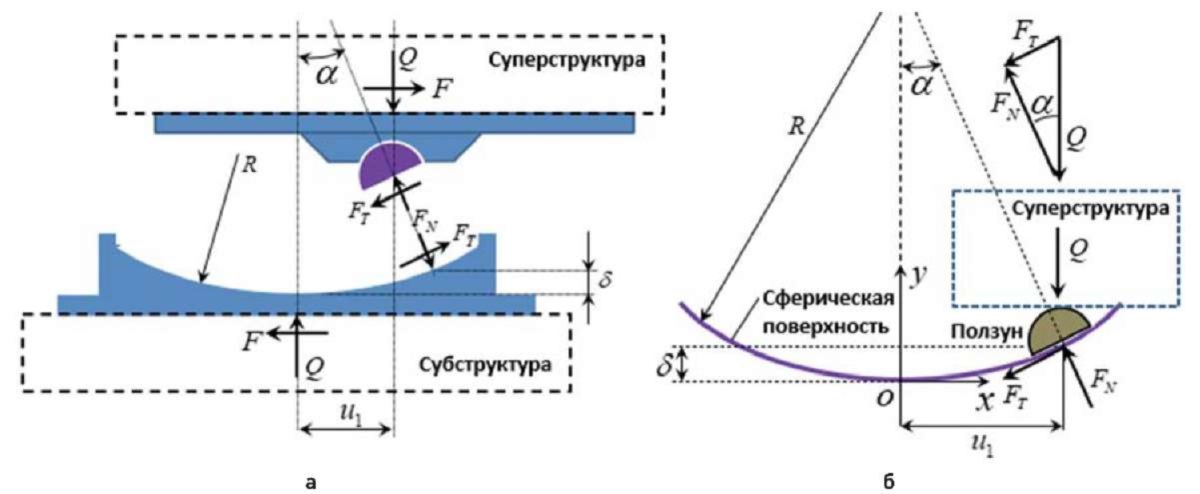
Рис. 2. Кинематика одномаятниковой скользящей опоры
Fig. 2. Kinematics of friction pendulum bearing
Тангенциальная сила как сила трения выражается через нормальную силу
FT = μFN , (3)
где μ – коэффициент трения.
Из (1) и (2) с учетом (3) получаем
F = FN(μcosα + sinα), Q = FN(cosα – μsinα),
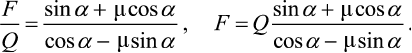 (4)
(4)
Из-за малости угла α можно предположить, что cosα – μsinα ≈ 1, тогда уравнение (4) можно представить в виде
F = Q(sinα + μcosα) = Q(u1/R + μcosα) = kh u1 + Qμcosα, (5)
F/Q = u1/R + μcosα,
где kh = k1 = Q/R – коэффициент горизонтальной жесткости ФМО;
Q, M – вес и масса суперструктуры: Q = M × g, M = m1 + m2 + ... + mn;
g – ускорение свободного падения.
Из (5) следует, что при R → ∞ и α → 0 горизонтальная сила F = μQ, что соответствует силе трения в обычной скользящей опоре.
Далее рассмотрим расчетную модель многоэтажного здания со скользящими одномаятниковыми опорами (рис. 1). В случае сейсмического воздействия, в момент времени t здание перемещается на величину u0, а за счет скольжения опоры перемещается еще на величину ub = u1, и только после этого оно деформируется (рис. 1а). Уравнение движения такой системы можно получить исходя из основной системы метода перемещений (рис. 1б). Систему уравнений движения можно получить исходя из равновесия каждой массы.
Уравнение динамического равновесия опорной массы здания mb = m1 (рис. 1в), с учетом затухания, представляется в виде
m1(ü0 + ü1) + chu•1 + F + r12u2 = 0, (6)
где r12 = –k2, k2 = 2 × 12EI/h23 – реакция в элементах первого этажа от единичного перемещения Z1 = 1;
ch = c1 – параметр затухания ФМО.
Сила F, которая состоит из суммы двух сил, представляется так:
F = kh × u1 + μQcosα × sgn(u•0 – u•1), (7)
kh = k1 = Q/R,
sgn(u•0 – u•1) – кусочно-постоянная нечетная функция действительного аргумента с областью определения (– ∞; + ∞) и областью значений (–1; 0; +1);
u•0 – скорость движения основания здания;
u•1 – скорость движения массы m1.
Подставив (7) в (6), получаем уравнение движения массы m1
m1 ü1 + c1 u•1 + μQcosα × sgn(u•0 – u•b) + k1u1 – k2u2 = – m1ü0(t), (8)
Функцию cosα(t) в (8) можно представить как производную от sinα(t) = u1(t)/R:
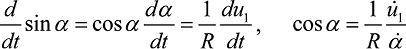 . (9)
. (9)
Если учесть, что круговая частота свободных колебаний математического маятника (рис. 2б) без учета и с учетом затухания соответственно равна:
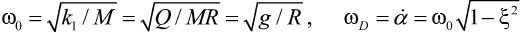 , (10)
, (10)
то уравнение (8), с учетом (9) и (10), можно представить в следующем виде
m1ü1 + c1u•1 + c0u•1 × usgn(u•0 – u•1) + k1u1 – k2u2 = – m1ü0(t), (11)
 .
.
Делим обе части (11) на m1 с учетом (10), где
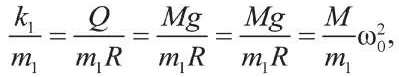 ,
,
получаем
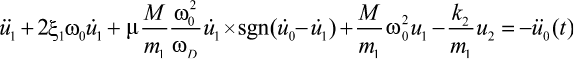 . (11а)
. (11а)
Коэффициент затухания ξ1 в (11а) зависит от фрикционных свойств материалов сферических поверхностей и ползунов, его можно принять в пределах от 10 до 30 % от критического затухания
ξ1 = ch/ccr; ccr = 2m1ω0; 0,1 ≤ ξ1 ≤ 0,3.
Уравнения движения массы mj и mn записываются в виде
mj(ü0 + ü1 + üj) + cju•j + rjj–1 uj–1 + rjj uj + rjj+1 uj+1 = 0,
ј = 2, 3, ..., n–1,
mn(ü0 + ü1 + üj) + cnu•j + rnn–1 un–1 + rnnun = 0,
здесь rjj–1 = – kj, rjj = kj + kj+1, rjj+1 = – kj+1, rnn–1 = – kn, rnn = kn,
mjüј + cju•j – kjuj–1 + (kj + kj+1)uj – kj+1 uj+1 = – mj(ü0 + ü1), (12)
üj + 2ωjξju•j – ω2juj–1 + (ω2j + ω2j+1)uj – ω2j+1uj+1 = – (ü0 + ü1),
ω2j = kj /mj , cj = ξccr = ξ2ωjmj, j = 2, 3, ..., n – 1.
Уравнение движения массы mn представляется в виде
mnün + cnu•n – knun–1 + kn un = – mn(ü0 + ü1), (13)
ün + 2ωnξnu•n – ω2nun–1 + ω2nun = – (ü0 + ü1),
ω2n = kn/mn.
Если предположить, что жесткости вертикальных элементов динамической модели здания стремятся к бесконечности, где относительные перемещения u2 = u3 = ... = un = 0, то задача сводится к рассмотрению уравнения
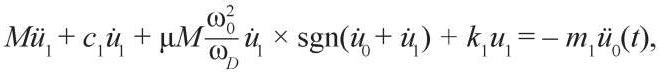
которое описывает движения абсолютно жесткого тела, установленного на фрикционно-маятниковых опорах.
Систему уравнений (11)–(13) можно представить в матричной форме
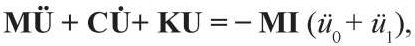 (14)
(14)
где M = diag(m1, m2, ..., mn) – диагональная матрица масс;
I – единичный вектор влияния;
C – матрица затухания.
Матрица жесткости и векторы перемещений, скоростей и ускорений представляются в виде
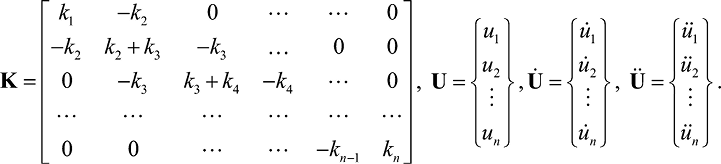 (15)
(15)
Матрицу затухания в (14), соответствующей верхней части здания в первом приближении, можно принять пропорционально матрице масс
C = diag(m2, m3, ..., mn) × a,
где a – коэффициент пропорциональности.
С целью численного моделирования задачи по расчету сейсмоизолированного здания с одномаятниковыми скользящими опорами используем метод последовательных аппроксимаций [2][3], в котором скорость и ускорения, соответствующие моменту времени tn, представляются в виде
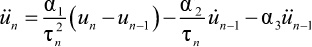 , (16)
, (16)
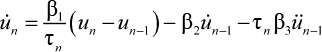 , (17)
, (17)
n = 1, 2, ..., N,
здесь τn – шаг интегрирования на отрезке времени [tn–1,tn];
αj, βj – коэффициенты аппроксимации [3–6].
Подставляя (16) и (17) в (11), получим
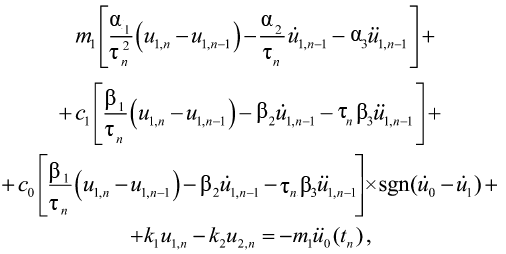 (18)
(18)
k1 = Q/R, k2 = 2 × 12EI/h23.
Уравнение (18) можно представить в виде
– a11u1,n – a12u2,n = m1 × us1,n–1 + c1 × sk1,n–1 + c0 × sk1,n–1 × sgn(u•0 + u•1) – m1ü0(tn),(19)
здесь
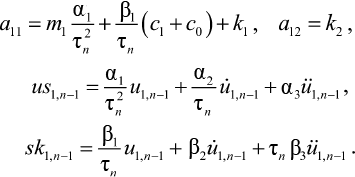
Проведя аналогичную процедуру к уравнению (12), получаем
– aj,i–1uj–1,n + ajjuj,n – ajj+1uj+1 = mj × usj,n–1 + cj × skj,n–1 – mj(ü0+ü1),(20)
здесь
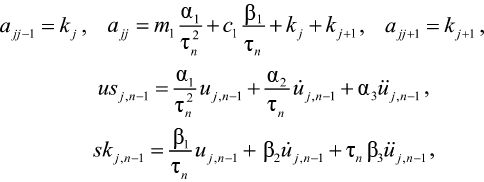
j = 2, 3, ..., n – 1.
Дифференциальное уравнение (13) с использованием аппроксимирующих формул (16) и (17) приводится к следующему виду
– ann–1un–1,n + an,nun,n = mn × usn,n–1 + cn × skn,n–1 – mn(ü0+ü1),(21)
где
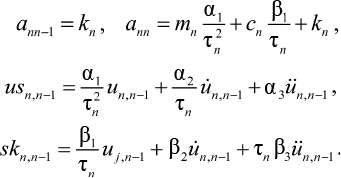
Полученные алгебраические уравнения (19)–(21) можно представить в матричной форме:
AU = B, (22)
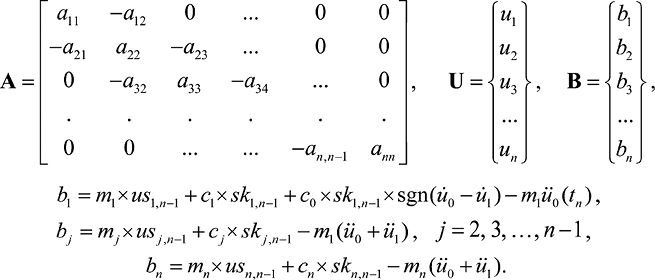 (23)
(23)
Система алгебраических уравнений (22) решается на каждом шаге по времени. Видно, что матрица A является ленточной, поэтому для ее решения можно использовать итерационный метод Зейделя.
Пример
Исследование динамической модели здания от действия мгновенного импульса. В качестве примера рассматривается 10-этажное каркасное здание со следующими геометрическими данными: размеры в плане – 18 × 36 м; сетка колонн – 6 × 6 м: высота этажа – 3 м, высота здания – 30 м. На опорной части здания установлены 28 фрикционно-маятниковых опор. Суммарная масса и суммарный вес здания соответственно равны:
M = 9 × 51,79 + 2 × 49,12 = 564,35 тс˖с²/м, Q = M × 9,81 = 5536,27 тс.
Изгибная жесткость и коэффициенты жесткости стоек и фрикционной опоры соответственно равны
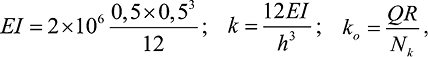
где R – радиус сферической поверхности опоры; Nk = 28 – количество опор.
На основе изложенной математической модели разработаны алгоритм и компьютерная программа FPB-1 (Friction pendulum bearings) и получены результаты для модели здания М1 – без сейсмоизоляции и модели М2 – с фрикционными опорами. Результаты для М2 получены при μ = 0,1, R = 5 м, ξ = 0,02 и при шаге численного интегрирования τ = 0,01 с. С целью анализа сходимости и точности результатов были проведены численные эксперименты при различных значениях шага по времени.
На рис. 3 приведены графики перемещения масс m1 (кривая 2) и m10 (кривая 1) модели М1, а также опорной массы mb = m1 (кривая 4) и массы m11 (кривая 3) модели М2. В табл. 1 приведены максимальные значения опрокидывающего момента и поперечной силы в опорной части, а также максимальные значения перемещения, скорости и ускорения, соответствующие массе перекрытия.
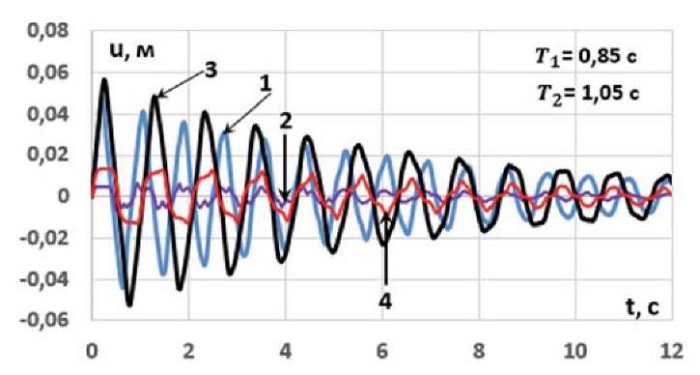
Рис. 3. Сравнение результатов колебания модели здания
Fig. 3. Comparison of vibration results of the building model
Таблица 1
Сравнение результатов
Table 1
Comparison of the results
|
Модель |
Mmax, тм |
Qmax, т |
umax, м |
u•max, м/с |
ümax, м/²с² |
|
М1 |
6,25 × 104 |
4,72 × 103 |
4,75 × 10–2 |
0,346 |
9,01 |
|
М2 |
3,69 × 104 |
2,53 × 103 |
5,63 × 10–2 |
0,255 |
5,97 |
Сравнение результатов показывает, что применение сейсмоизоляции в виде фрикционно-маятниковых опор (модель М2) приводит к значительному уменьшению внутренних усилий в опорной части, а также к уменьшению скорости и ускорения в верхней части здания по сравнению с моделью М1. При этом несколько увеличиваются перемещения как в нижней, так и верхней частях исследуемого объекта.
Вывод
Разработаны математическая модель и алгоритм расчета, которые позволяют исследовать сейсмоизолированные здания при различных воздействиях, в том числе сейсмических в виде заданной акселерограммы землетрясения. В результате численного моделирования динамической задачи здания с применением метода последовательных аппроксимаций разработана компьютерная программа и получены результаты, которые сопоставлены с данными аналогичной модели без сейсмозащиты. Применение сейсмоизоляции в виде фрикционно-маятниковых опор приводит к значительному уменьшению внутренних усилий в сечениях исследуемого объекта по сравнению с аналогичным объектом без сейсмоизоляции.
Список литературы
1. Свод правил. Здания сейсмостойкие и сейсмоизолированные. Правила проектирования. Москва: Минрегион России; 2013.
2. <i>Ozer M.</i> The linear formulation for the equations of the dynamic responses of rigid and flexible structures supported by friction pendulum sliding (fps) bearings. In: 13th World Conference on Earthquake Engineering [internet]; 2004 August 1–6; Vancouver, B.C., Canada, Paper No. 1675. Available at: https://www.iitk.ac.in/nicee/wcee/article/13_1675.pdf
3. <i>Kelly J.M.</i> Aseismic base isolation: Review and bibliography. Soil Dyn. Earthq. Eng. 1986;5(4):202–216. https://doi.org/10.1016/0267-7261(86)90006-0
4. <i>Низомов Д.Н.</i> Методы прямого интегрирования дифференциальных уравнений движения дискретных систем. В: Строительство и архитектура: сб. науч. тр. Таджикского технического университета. Душанбе: ТТУ; 1992. Вып. 2, с. 39–46.
5. <i>Низомов Д.Н.</i> Численные методы решения динамических задач строительной механики. Изв. АН Респ. Тадж. Отделение физико-математических, химических, геологических и технических наук. 1993;(1):62–72.
6. <i>Низомов Д.Н.</i> Проблемы сейсмостойкого строительства в Таджикистане. Строительствo и архитектура. 2010;(5):25–27.
7. <i>Низомов Д.Н., Каландарбеков И., Каландарбеков И.И.</i> Численное моделирование динамической системы «платформа – модель – здания». Вестник гражданских инженеров. 2018;(3):66–72.
8. <i>Низомов Д.Н., Каландарбеков И., Ходжибоев А.А.</i> Концепция сейсмоизоляции как стратегия в области сейсмостойкого строительства. В: Практика, проблемы и перспективы повышения качества проектирования, строительства и производства строительных материалов. Материалы респ. конф.; 2016; Душанбе; 2016, с. 139–147.
9. <i>Низомов Д.Н., Каландарбеков И., Ходжибоев А.А.</i> Численный анализ модели сейсмоизолированного многоэтажного здания. Сейсмостойкое строительство. Безопасность сооружений. 2017;(3):16–20.
10. <i>Низомов Д.Н., Каландарбеков И.К., Каландарбеков И.И.</i> Численное моделирование сейсмоизолированных зданий с сухим трением. Доклады Академии наук Республики Таджикистан. 2018;61(1):47–53.
11. <i>Низомов Д.Н., Каландарбеков И.К., Каландарбеков И.И.</i> Исследования свободных колебаний зданий с учетом сейсмоизоляции. Труды Института геологии, сейсмостойкого строительства и сейсмологии АН Респ. Таджикистан. Душанбе, с. 182–189.
Об авторах
Д. Н. НизомовТаджикистан
Джахонгир Низомович Низомов, д-р техн. наук, профессор, член-корреспондент НАНТ, заведующий лабораторией сейсмостойкости зданий и сооружений
e-mail: tiees@mail.ru
А. М. Сангинов
Таджикистан
Абдусамад Мирвафоевич Сангинов, канд. техн. наук, ведущий научный сотрудник лаборатории сейсмостойкости зданий и сооружений
e-mail: samad80@mail.ru
Рецензия
Для цитирования:
Низомов Д.Н., Сангинов А.М. Численное моделирование сейсмоизолированных зданий с фрикционно-маятниковыми опорами. Вестник НИЦ «Строительство». 2023;38(3):143-154. https://doi.org/10.37538/2224-9494-2023-3(38)-143-154. EDN: YGFQNY
For citation:
Nizomov D.N., Sanginov A.M. Numerical simulation of seismically isolated buildings with friction pendulum bearings. Bulletin of Science and Research Center of Construction. 2023;38(3):143-154. (In Russ.) https://doi.org/10.37538/2224-9494-2023-3(38)-143-154. EDN: YGFQNY


























