Перейти к:
Особенности построения конечно-элементной расчетной модели трубчатой башни ветроагрегата
https://doi.org/10.37538/2224-9494-2023-4(39)-7-27
EDN: HFKNZG
Аннотация
Введение. Не вызывает сомнений актуальность проблемы выявления особенностей моделирования сооружений башенного типа, что позволит упростить работу инженера и в то же время выйти на качественно новый уровень в принятии проектных решений.
Целью данной работы является комплексная оценка влияния особенностей создания расчетной схемы на результирующий параметр – частотное поведение трубчатой башни под ветроэнергетические установки
Материалы и методы. Численные исследования проведены в отечественном ПВК SCAD Office. При создании расчетных моделей использованы типы КЭ 41, 42, 44 и 50. При определении оценки влияния типа конечного элемента были произведены расчеты цилиндрической башни с фиксированными параметрами с учетом изменений типа и размера КЭ. При расчетах оценивающими факторами являлись: изменение напряжений, а также изменение частоты первой формы собственных колебаний. При сравнении значений напряжений в качестве расчетной принималась пластина третьего ряда от закрепленного основания. В качестве ветроагрегатов рассмотрены установки Turbowind T600–48 и Eviag EV 100.
Результаты. Достаточную величину дискретизации расчетной схемы для определения частоты собственных колебаний следует принимать nR = 12, т. к. дальнейшее увеличение значения nR приведет к изменению частоты собственных колебаний менее чем на 1 %. Определены фиксированные частоты для ветроагрегата Eviag EV 100, равные 0,275 и 0,825 Гц. Для Turbowind T600–48 определен диапазон резонансных частот по причине наличия переменной частоты вращения ротора: диапазон стартовых частот – от 0,255 до 0,765 Гц, а диапазон максимальных частот – от 0,383 до 1,149 Гц.
Выводы. При формировании расчетной схемы башни в ПВК SCAD рационально использовать 44-й тип конечного элемента с учетом полученной достаточной величины дискретизации. Полученный спектр собственных и резонансных частот позволяет при принятии проектных решений избежать появления резонансного эффекта.
Ключевые слова
Для цитирования:
Гаранжа И.М., Танасогло А.В., Писарева М.М. Особенности построения конечно-элементной расчетной модели трубчатой башни ветроагрегата. Вестник НИЦ «Строительство». 2023;39(4):7-27. https://doi.org/10.37538/2224-9494-2023-4(39)-7-27. EDN: HFKNZG
For citation:
Garanzha I.M., Tanasoglo A.V., Pisareva M.M. Features of a finite-element modeling of a tubular tower for a wind-power unit. Bulletin of Science and Research Center of Construction. 2023;39(4):7-27. (In Russ.) https://doi.org/10.37538/2224-9494-2023-4(39)-7-27. EDN: HFKNZG
Введение
На сегодня повсеместно расчет и проектирование конструкций выполняются с использованием метода конечных элементов, реализованного как в различных зарубежных (ANSYS, NASTRAN, RSA, Sap2000, Abaqus, Etabs) [1–4], так и в отечественных программных комплексах (Lira SAPR, Lira 10, SCAD и др.), которые требуют определения особенностей создания расчетной схемы (тип и размер конечного элемента, условия сопряжения элементов в пространстве и т. д.) [5–8]. Данный подход к решению численных задач позволяет рассчитывать на максимальный уровень качества проектных решений при условии создания адекватной и в то же время простой в исполнении расчетной модели, что напрямую определяет уровень точности получаемых результатов при определении параметров напряженно-деформированного состояния (НДС), а также динамических характеристик зданий и сооружений. Проектировщику принципиально необходимо знать степень влияния различных факторов при создании конечно-элементной расчетной модели на динамический отклик объекта проектирования. Следовательно, не вызывает сомнений актуальность проблемы выявления особенностей моделирования сооружений башенного типа, что позволит упростить работу инженера и в то же время выйти на качественно новый уровень в принятии проектных решений в области ветроэнергетики в частности, находящейся сегодня на стадии активного становления и развития и оказывающей значимое влияние на энергетическую отрасль России. Вопросы, связанные с созданием и рационализацией КЭ-моделей трубчатых башенных сооружений, уже рассматривались в работах [9–14]. Непосредственно моделированию ветроэнергетических объектов в России и за рубежом посвящены исследования [15–21]. Но их результаты в полной мере не отражают особенностей моделирования вышеупомянутых конструкций и не в достаточном объеме дают представление о зависимости между геометрическими размерами башен, их напряженным состоянием и динамическими характеристиками. В связи с чем целью данной работы является комплексная оценка влияния особенностей создания расчетной схемы на результирующий параметр – частотное поведение трубчатой башни под ветроэнергетические установки Turbowind T600-48 и Eviag EV 100, наиболее популярные на ветростанциях России за последние два десятилетия [22–24]. Для проведения численных исследований использован отечественный проектно-вычислительный комплекс SCAD Office [5][14].
Для достижения поставленной цели решены следующие задачи:
- определен рациональный тип конечного элемента при моделировании трубчатой конусообразной башни;
- выявлен достаточный уровень дискретизации расчетной модели;
- выполнена оценка влияния размеров башни на параметры ее НДС и частотные характеристики, учитывая вариации геометрических параметров (высота, диаметр у основания, толщина стенки башни);
- сравнительно изучено изменение напряжений между цилиндрической башней кольцевого и многогранного сечения;
- определены геометрические параметры башен, частота собственных колебаний которых попадает между диапазонами вынужденных колебаний ротора ВЭУ, для избегания попадания конструкции в резонансное состояние еще на этапе конструирования объекта.
Предметом исследования в данной работе являются параметры НДС и частотные характеристики трубчатой башни под ветроэнергетические установки.
В качестве объекта исследования принята конструкция стальной трубчатой башни под ветроэнергетические установки.
Материалы и методы
Программный комплекс SCAD автоматически определяет тип конечного элемента в зависимости от заданной расчетной схемы. Однако тип конечного элемента пользователь может изменить вручную, при изменении КЭ возможны расхождения в результатах расчета. Универсальные конечные элементы, описанные ниже, предназначены для расчета тонких пологих оболочек. Каждый узел конечных элементов имеет по шесть степеней свободы [5][14]:
- U, V, W– линейные перемещения по осям X, Y и Z;
- угол поворота относительно оси OX, положительное направление которого противоположно направлению вращения часовой стрелки, если смотреть с конца оси;
- угол поворота относительно оси OY, положительное направление которого противоположно направлению вращения часовой стрелки, если смотреть с конца оси;
- угол поворота относительно оси OZ.
Степени свободы U, V отвечают мембранным, а W, UX, UY – изгибным деформациям. Угол поворота UZ в местной системе координат элемента всегда равен нулю. Он вводится для стыковки элементов, не лежащих в одной плоскости, и необходим для пространственной работы конструкции.
Введение шарниров в узлах элементов не допускается.
Материал пластины может быть изотропным, ортотропным и анизотропным.
Произвести расчет пластинчатых элементов возможно при использовании следующих типов конечных элементов:
- прямоугольный (тип 41), рис.1а;
- треугольный (тип 42), рис.1б;
- четырехугольный (тип 44), рис.1в;
- четырехугольный с числом узлов от четырех до восьми (тип 50), рис.1г. Кроме вершин четырехугольника на каждой из сторон может находиться еще по одному узлу. Нумерация узлов с 5-го по 8-й произвольная.
Порядок задания первых четырех (трех) узлов элементов приведен на рис. 1а–г.
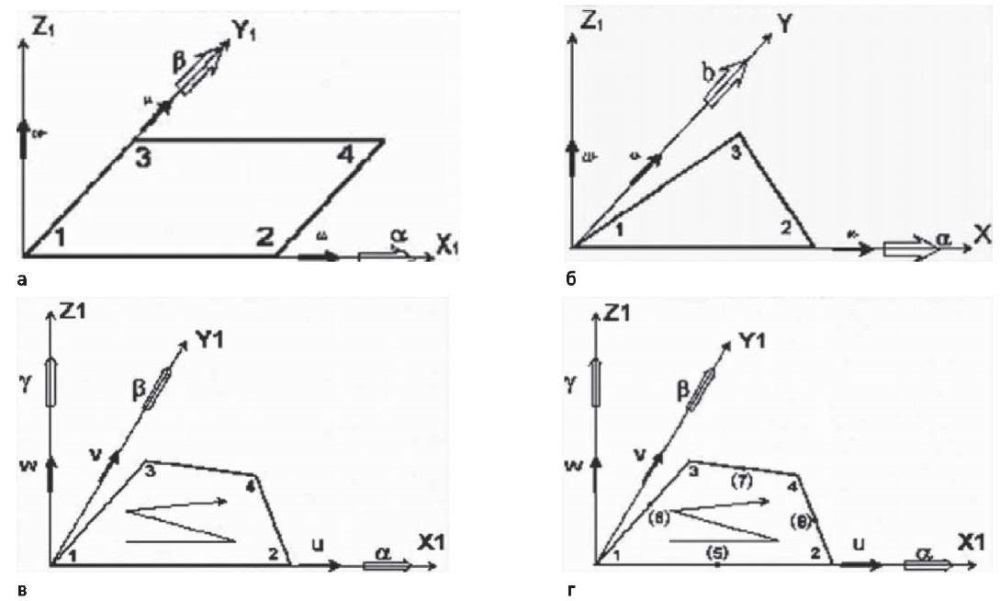
Рис. 1. Типы конечных элементов
Fig. 1. Finite element types
Все элементы оболочки имеют местную систему координат X1 Y1 Z1, в которой ось X1 проходит от первого узла ко второму, ось Y1 лежит в плоскости элемента ортогонально X1 и направлена в сторону третьего узла, а ось Z1 образует с осями X1 и Y1 правую тройку.
Во всех элементах оболочки тангенциальные и нормальное перемещения аппроксимировались независимо. Использовались функции элементов такой же формы для расчета плит и балок стенок.
Если в соответствующей строке документа «жесткости» не задана система координат выдачи усилий, то по умолчанию усилия вычисляются в местной системе координат элемента. В центре тяжести элемента и, по требованию, в узлах вычисляются усилия NX, NY, τXY, MX, MY, MXY, QX, QY (при наличии упругого основания RZ) и узловые реакции Rxi, Ryi, Rzi, RUXi, RUYi, RUZi.
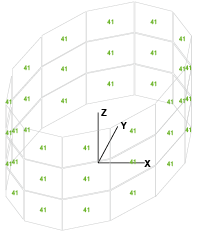
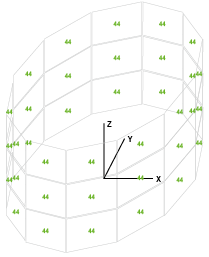
При определении оценки влияния типа конечного элемента, применяемого для расчета трубчатой башни ВЭУ, были произведены расчеты цилиндрической башни с фиксированными параметрами (рис. 2). Оценка выполнялась с точки зрения влияния типа КЭ на частоту собственных колебаний.

Рис. 2. Схема башни
Fig. 2. Scheme of a tower
При расчетах оценивающими факторами являлись: изменение главных (σX, σY, τXY) и эквивалентных напряжений (σ), а также изменение частоты первой формы собственных колебаний. При сравнении значений главных и эквивалентных напряжений в качестве расчетной принималась пластина третьего ряда от основания. Это делалось для того, чтобы на значение напряжений не повлияло явление краевого эффекта, присутствующее у пластин, защемленных в основании (для КЭ 41, 44, 50), и среднее значение напряжений в четырех пластинах третьего ряда (для КЭ 42). Результаты расчета напряжений представлены в табл. 1. В таблице приведены значения нормальных и касательных напряжений, а также рассчитаны значения суммарных напряжений, вычисленных по формуле (1):
σ = N2x + N2y – Nx × Ny + 3 × τ2xy ≤ 1,15 × R × γсσ = N2x + N2y – Nx × Ny + 3 × τ2xy ≤ 1,15 × R × γс (1)
Таблица 1
Значения нормальных и касательных напряжений при изменении типа КЭ
Table 1
Values of normal and shear stresses for various FE types
|
Тип КЭ |
Фрагмент КЭ модели |
Напряжения, МПа |
|||
|
σX |
σY |
τXy |
σ |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
41 |
|
8,93 |
-0,01 |
8,93 |
47,11 |
|
42 |
|
8,87 |
-0,01 |
8,88 |
46,69 |
|
44 |
|
8,93 |
-0,01 |
8,93 |
47,11 |
|
50 |
|
8,98 |
0,00 |
8,93 |
47,12 |
Результаты исследования и обсуждения
Диаграмма изменения суммарных напряжений приведена на рис. 3.
Помимо значений напряжений учитывалась частота «первой» формы собственных колебаний башни. Первой формой является изгибная форма колебаний, представленная на рис. 4.
Значения частот собственных колебаний представлены в табл. 2.
Диаграмма изменения частот собственных колебаний при изменении типа конечного элемента предоставлена на рис. 5.
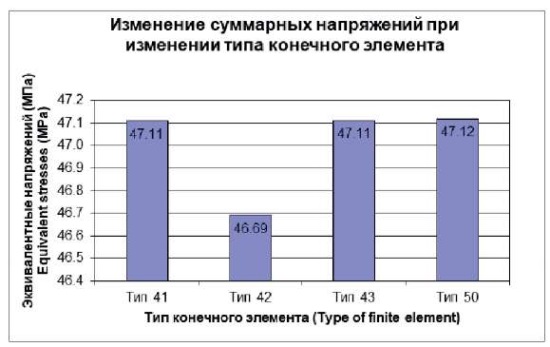
Рис. 3. Изменение эквивалентных напряжений при изменении типа КЭ
Fig. 3. Variations in equivalent stresses for various FE types

Рис. 4. Первая «изгибная» форма колебаний башни
Fig. 4. First “bending” mode of tower oscillations
Таблица 2
Значения частот собственных колебаний
Table 2
Frequency values of natural oscillation
|
Тип КЭ |
Частота собственных колебаний, Гц |
|
41 |
11,19 |
|
42 |
11,22 |
|
44 |
11,19 |
|
50 |
18,06 |
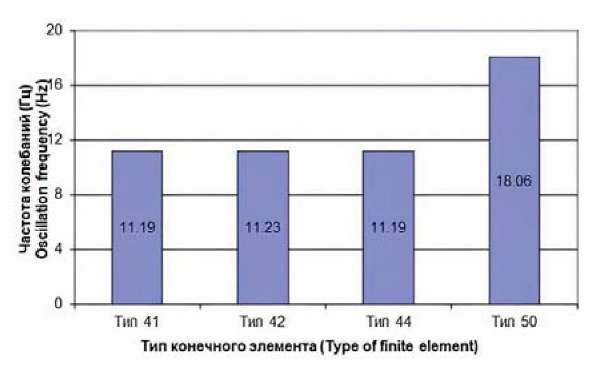
Рис. 5. Изменение частоты собственных колебаний при изменении типа КЭ
Fig. 5. Variations in the frequency of natural oscillations for various FE types
Оценка влияния размера конечного элемента на результаты расчета
Первым шагом при проектировании любой конструкции является создание расчетной схемы. Последняя должна наиболее точно характеризовать проектируемую конструкцию, однако ее схема должна быть как можно проще. При расчете цилиндрических, а также конусообразных металлических башен в программном комплексе SCAD необходимо задать несколько параметров. Помимо высоты, диаметров у основания и у оголовка, толщины стенки оболочки SCAD требует ввода количества сегментов. Программа представляет цилиндр в виде оболочки, состоящей из множества пластин. Целью нижеизложенных исследований является оценка влияния размера конечного элемента на результаты расчета.
В качестве расчетных были приняты конструкции башен цилиндрической формы. Изменяемыми параметрами были:
- диаметр башни, D;
- высота конструкции, H.
Анализируемые габариты башен приведены в табл. 3.
Таблица 3
Анализируемые габариты башен
Table 3
Analyzed tower dimensions
|
D, м |
Высота башни, м, при H/D |
|||
|
H/D = 5 |
H/D = 7 |
H/D = 10 |
H/D = 13 |
|
|
3 |
15 |
21 |
30 |
39 |
|
5 |
25 |
35 |
50 |
65 |
|
8 |
40 |
56 |
80 |
104 |
Помимо изменения геометрических характеристик производилась дискретизация построения каждой расчетной схемы. Параметром дискретизации являлось число элементов в основании схемы, запрашиваемое программным комплексом (рис. 6).
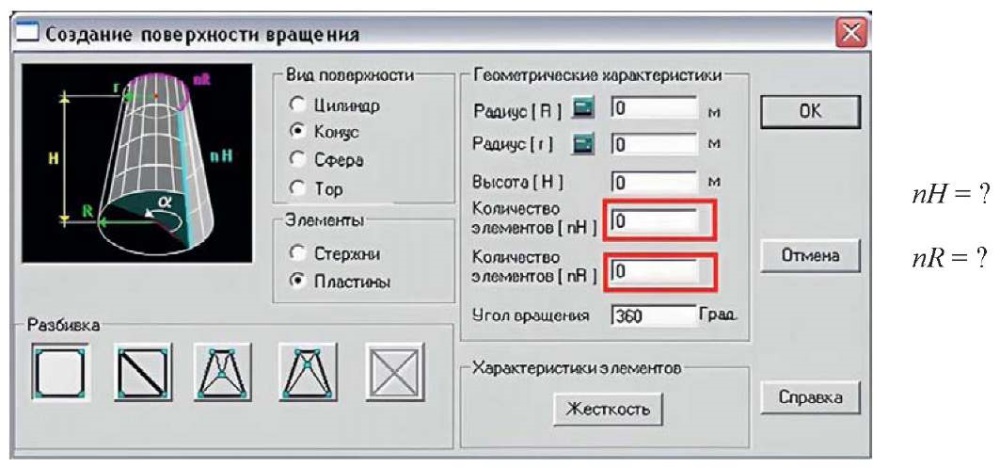
Рис. 6. Требуемые параметры расчетной схемы
Fig. 6. Required computational model parameters
На рис. 6 в качестве искомых параметров дискретизации расчетной модели стойки приведены: nH – количество элементов по высоте схемы и nR – количество элементов в основании схемы.
Таким образом, каждая конструкция башни с фиксированными параметрами высоты и диаметра была просчитана при количестве элементов в основании nR. Соотношение ширины и высоты единичной пластины 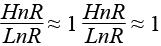 (рис. 7).
(рис. 7).
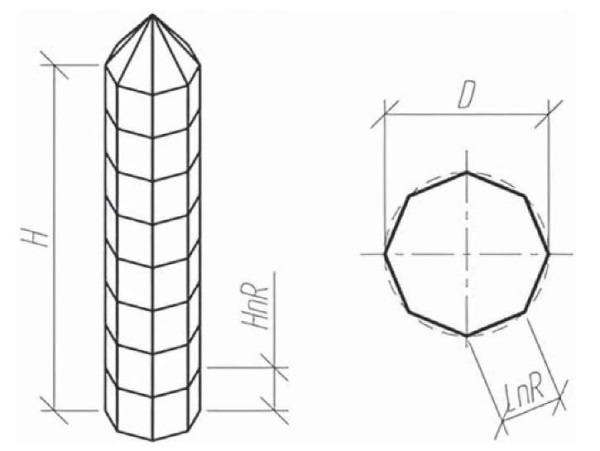
Рис. 7. Размеры конечного элемента
Fig. 7. Finite element dimensions
Параметр nH определялся по формуле 2:
nH ≈ H × nR2π × R. (2)
Пример 1. Башня диаметром у основания 3 м и высотой 15 м была рассчитана при nR = 6, 8, 10, 12, 14, 16. Исходные данные для расчета, а также результат расчета – частота собственных колебаний башни приведены в табл. 4.
Таблица 4
Изменение частоты собственных колебаний при различном значении nR
Table 4
Variations in the frequency of natural oscillations at various nR values
|
H, м |
D, м |
nR |
nH |
ν, Гц |
|
15 |
3 |
6 |
10 |
1,507 |
|
8 |
13 |
1,177 |
||
|
10 |
16 |
0,942 |
||
|
12 |
19 |
0,785 |
||
|
14 |
22 |
0,671 |
||
|
16 |
25 |
0,588 |
Аналогичным образом были произведены расчеты для башен (табл. 3). После определения частоты собственных колебаний башен с различными геометрическими параметрами, а также с различным уровнем дискретизации единичных пластин были построены графики зависимости частоты башни от величины дискретизации, а также определена относительная погрешность между предыдущим и последующим уровнями дискретизации. Для D = 3 м (см. табл. 5 и рис. 8), для D = 5 м (см. табл. 6 и рис. 9), для D = 8 м (см. табл. 7 и рис. 10).
Таблица 5
Изменение частоты собственных колебаний башни (D = 3 м)
Table 5
Variations in the frequency of tower natural oscillations (D = 3 m)
|
R, м |
nR |
H/D = 5 |
H/D = 7 |
H/D = 10 |
H/D = 13 |
||||
|
ν |
% |
ν |
% |
ν |
% |
ν |
% |
||
|
3 |
6 |
5,17 |
– |
3,13 |
– |
2,73 |
– |
1,68 |
– |
|
8 |
5,34 |
3,4 |
3,23 |
3,2 |
2,81 |
2,9 |
1,72 |
2,4 |
|
|
10 |
5,42 |
1,5 |
3,28 |
1,6 |
2,85 |
1,4 |
1,74 |
1,2 |
|
|
12 |
5,47 |
0,8 |
3,31 |
0,8 |
2,87 |
0,6 |
1,76 |
0,9 |
|
|
14 |
5,49 |
0,5 |
3,32 |
0,5 |
2,88 |
0,4 |
1,76 |
0,4 |
|
|
16 |
5,51 |
0,3 |
3,33 |
0,3 |
2,89 |
0,3 |
1,77 |
0,3 |
|
Таблица 6
Изменение частоты собственных колебаний башни (D = 5 м)
Table 6
Variations in the frequency of tower natural oscillations (D = 5 m)
|
R, м |
nR |
H/D = 5 |
H/D = 7 |
H/D = 10 |
H/D = 13 |
||||
|
ν |
% |
ν |
% |
ν |
% |
ν |
% |
||
|
5 |
6 |
4,48 |
– |
3,39 |
– |
1,74 |
– |
1,05 |
– |
|
8 |
4,61 |
3,0 |
3,47 |
2,3 |
1,78 |
2,5 |
1,08 |
2,7 |
|
|
10 |
4,68 |
1,4 |
3,51 |
1,2 |
1,80 |
1,1 |
1,09 |
1,3 |
|
|
12 |
4,71 |
0,7 |
3,54 |
0,6 |
1,82 |
0,8 |
1,10 |
0,7 |
|
|
14 |
4,73 |
0,4 |
3,55 |
0,4 |
1,82 |
0,4 |
1,10 |
0,4 |
|
|
16 |
4,75 |
0,3 |
3,56 |
0,2 |
1,83 |
0,3 |
1,11 |
0,3 |
|
Таблица 7
Изменение частоты собственных колебаний башни (D = 8 м)
Table 7
Variations in the frequency of tower natural oscillations (D = 8 m)
|
R, м |
nR |
H/D = 5 |
H/D = 7 |
H/D = 10 |
H/D = 13 |
||||
|
ν |
% |
ν |
% |
ν |
% |
ν |
% |
||
|
8 |
6 |
3,45 |
– |
2,18 |
– |
1,11 |
– |
0,67 |
– |
|
8 |
3,54 |
2,7 |
2,23 |
2,2 |
1,14 |
2,5 |
0,69 |
2,6 |
|
|
10 |
3,58 |
1,2 |
2,26 |
1,1 |
1,15 |
1,1 |
0,69 |
1,2 |
|
|
12 |
3,61 |
0,6 |
2,27 |
0,6 |
1,16 |
0,7 |
0,70 |
0,7 |
|
|
14 |
3,62 |
0,4 |
2,28 |
0,4 |
1,16 |
0,4 |
0,70 |
0,4 |
|
|
16 |
3,63 |
0,2 |
2,28 |
0,2 |
1,16 |
0,3 |
0,70 |
0,3 |
|
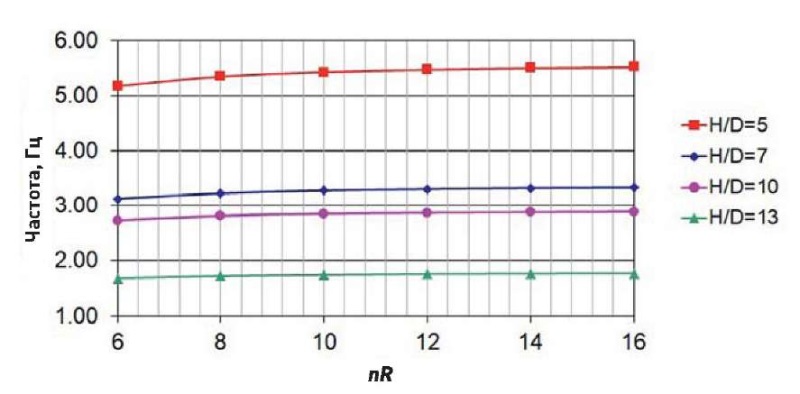
Рис. 8. Изменение частоты собственных колебаний башни (D = 3 м)
Fig. 8. Variations in the frequency of tower natural oscillations (D = 3 m)
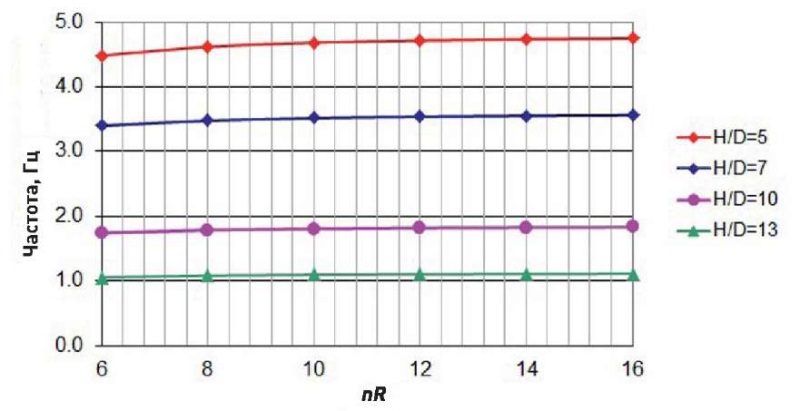
Рис. 9. Изменение частоты собственных колебаний башни (D = 5 м)
Fig. 9. Variations in the frequency of tower natural oscillations (D = 5 m)
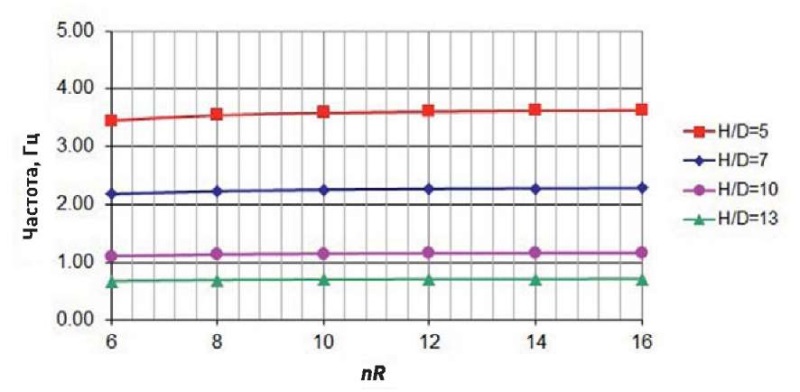
Рис. 10. Изменение частоты собственных колебаний башни (D = 8 м)
Fig. 10. Variations in the frequency of tower natural oscillations (D = 8 m)
С увеличением значения nR при расчете частоты собственных колебаний точность результатов незначительно повышается, однако и усложняется анализ расчетной схемы. С каждым последующим увеличением величины дискретизации количество элементов увеличивается в геометрической прогрессии. Проанализировав полученные результаты, можно сделать вывод, что достаточный уровень дискретизации составляет 12 элементов, т. к. дальнейшее увеличение значения nR приведет к изменению частоты собственных колебаний менее чем на 1 %.
Принятое для дальнейших расчетов значение дискретизации nR = 12 достаточно для динамических расчетов конструкций, определения частоты собственных колебаний. Необходимо оценить относительную погрешность в определении напряжений. Программный комплекс SCAD позволяет определить значение напряжений в срединной точке единичной пластины. Изменяя значение дискретизации, изменяется и геометрические размеры КЭ.
Пример 2. Рассмотрим опорный участок расчетной схемы цилиндрической башни с высотой H и диаметром основания D, но при различных значениях числа дискретизации. Рассмотрим пластину третьего ряда от основания, дабы пренебречь явлением краевого эффекта (рис. 11).
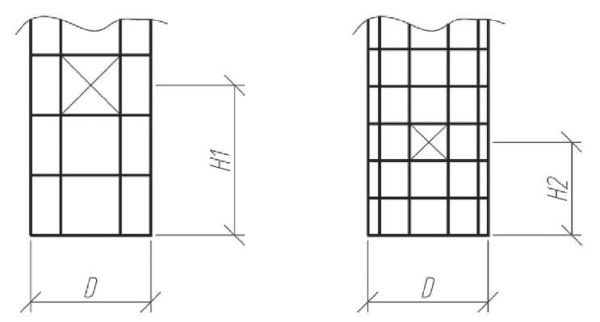
Рис. 11. Абсолютная высота расчетного КЭ при различном уровне дискретизации
Fig. 11. Absolute height of a computational FE at various discretization levels
При неизменяемых геометрических параметрах башни (высота, диаметр основания) были получены различные значения напряжения в точках с различной абсолютной высотой. Поэтому определить изменение значений напряжений при различной степени дискретизации невозможно из-за высокой погрешности. Для этого необходимо использовать альтернативный подход.
Упростив расчетную схему башни до вертикального жестко защемленного у основания консольного стержня, можно определить напряжения как отношение изгибающего момента к моменту сопротивления. Изменение напряжений между цилиндрической башней с моментом сопротивления WКОЛЬЦА и башней, имеющей в сечении 12-угольник с Wn = 12, не превышает 5 %. В рамках расчетов по изучению частотного поведения башни ВЭУ это не приведет к значительным погрешностям и является допустимым, т. к. изменение толщины стенки на 1–2 мм приведет к изменению частоты на 0,5 %.
Оценка влияния размеров трубчатой башни ветроагрегата на НДС и частотные характеристики
Воздействия от ВЭУ часто являются источником сильных вибраций. Возбуждение происходит главным образом на двух частотах:
- основная частота f*, которая определена числом оборотов ротора в единицу времени;
- дополнительная частота f**, которая определена проходом лопастей мимо башни (f**= nf*, где n – количество лопастей ротора).
В пределах 20-летнего срока прогнозируемой эксплуатации ВЭУ при ежегодной работе 2000–3000 часов и скорости ротора 40–70 оборотов в минуту башня противостоит более чем 10⁸ циклам нагружения. Это требует использования специальных методов для вычисления выносливости, основанных на теории накопления эффекта повреждений, что особенно важно для сварной трубчатой опоры под ВЭУ большой мощности.
Для башен с первой собственной частотой f01 < f** должно рассматриваться явление стартового резонанса при выходе на расчетный режим и при остановке.
При проектировании башен необходимо выполнение условий для отношения частоты вращения ветротурбины f** к первой частоте собственных колебаний системы «башня – ВЭУ» f01 согласно [25].
Согласно закону деформирования бетона Мандера вышеупомянутые характеристики определяются по (3):
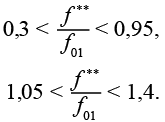 (3)
(3)
Это может достигаться за счет увеличения жесткости конструкции башни.
Были произведены расчеты по определению частоты собственных колебаний трубчатых башен с различными геометрическими характеристиками. Задачей этих расчетов было определение изменений частотных характеристик конструкции при увеличении высоты, диаметра у основания, толщины стенки башни. Неизменным оставался лишь диаметр башни у оголовка d = 2 м, который регламентировался заводом-производителем ветроагрегата Turbowind T600-48.
Определение частотных характеристик производилось в программном комплексе SCAD, с построением расчетных моделей, имеющих основные параметры, указанные на рис. 2:
- величина дискретизации по окружности составляет nR= 12;
- высота единичной пластины приблизительно равна ее ширине HnR≈ LnR.
Основные геометрические характеристики анализируемых башен приведены на рис. 12 и 13. Особенностью расчетной модели башен является изменение жесткостных характеристик конструкции по высоте. Каждая башня условно была разделена на 20-метровые секции по высоте. Толщина стенки верхней секции для Turbowind T600-48 составляла 16 мм и увеличивалась на 1 порядок (согласно сортаменту листовой стали) для нижележащей секции, соответственно для Eviag EV 100 толщина верхней секции составляла 18 мм и увеличивалась на 1 порядок для нижележащей секции.
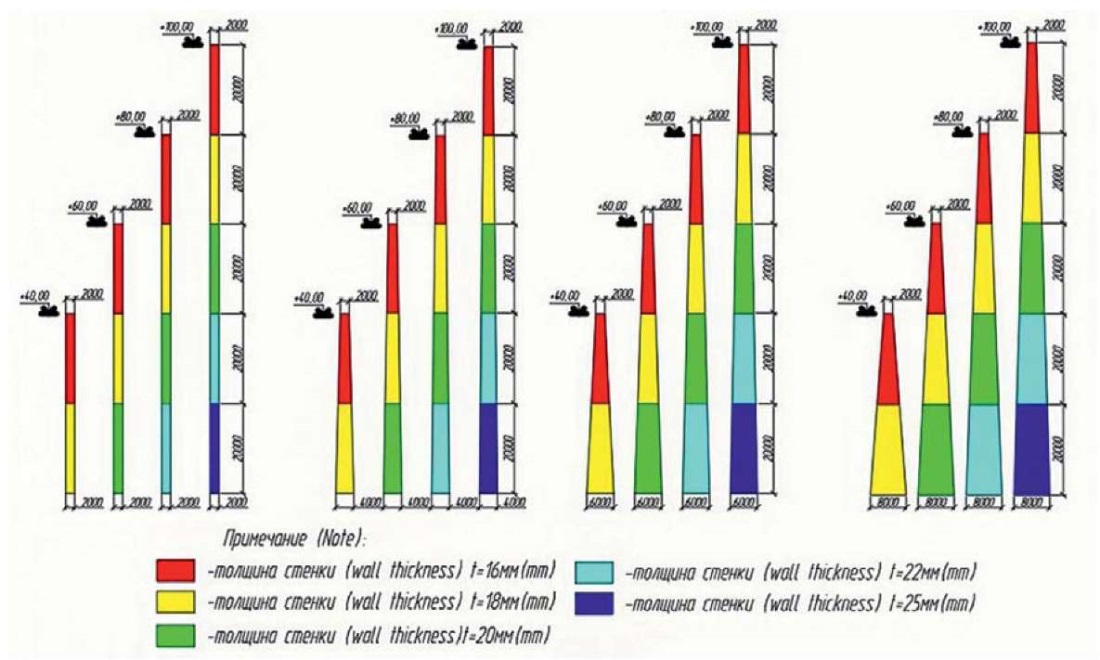
Рис. 12. Расчетные габариты башен для Turbowind T600-48
Fig. 12. Calculated dimensions of Turbowind T600–48 towers

Рис. 13. Расчетные габариты башен для Eviag EV 100
Fig. 13. Calculated dimensions of Eviag EV 100 towers
Для увеличения жесткости конструкции на границах секций в расчетную схему были введены диафрагмы (пластины толщиной 10 мм).
Массы внутренних лестниц, ограждений, коммуникаций не учитывались из-за незначительной величины
Масса ротора (с лопастями) и гондолы ветроагрегатов Turbowind T600-48 была представлена в виде сосредоточенной в точке массы, находившейся по (4):
M = Mp + MГ (4)
и составляет для Turbowind T600-48 – 41 т, а для Eviag EV 100 – 81 т.
Для Eviag EV 100 характерна постоянная скорость вращения ротора, поэтому резонансные частоты имеют конкретное значение:
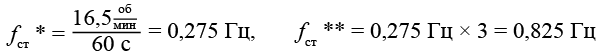 .
.
Основной задачей являлось определение геометрических параметров башен, частота собственных колебаний которых попадает между диапазонами вынужденных колебаний ротора ВЭУ. При анализе рис. 14 и 15 был сделан вывод о том, что наиболее удовлетворяющими требованиям формулы 4 являются башни высотой от 60 до 80 м и диаметром основания 4–6 м (для Turbowind T600-48), высотой от 90 до 100 м и диаметром основания 8 м (для Eviag EV 100).
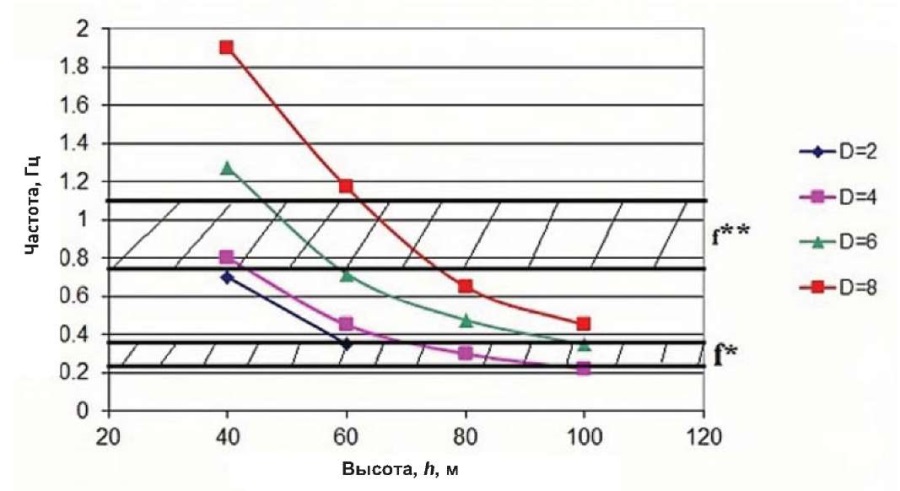
Рис. 14. Изменение частоты собственных колебаний башни c Turbowind T600–48
Fig. 14. Variations in the frequency of natural oscillations
for a Turbowind T600–48 tower
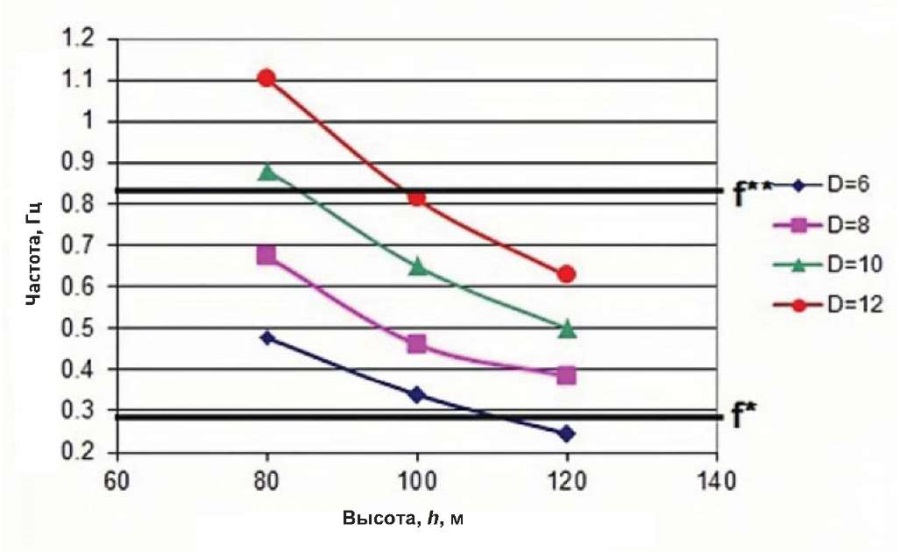
Рис. 15. Изменение частоты собственных колебаний башни с Eviag EV 100
Fig. 15. Variations in the frequency of natural oscillations for an Eviag EV 100 tower
Методика определения рациональной высоты ветроагрегата зависит не только от частоты собственных колебаний конструкции, но и от ряда других факторов:
- потенциальной выработки ветроагрегата;
- массы конструкции;
- стоимости монтажа и дальнейшего обслуживания.
В последующих расчетах определяется рациональная высота размещения ВЭУ с учетом всех вышеупомянутых показателей. График изменения массы конструкций башен показан на рис. 16, 17.
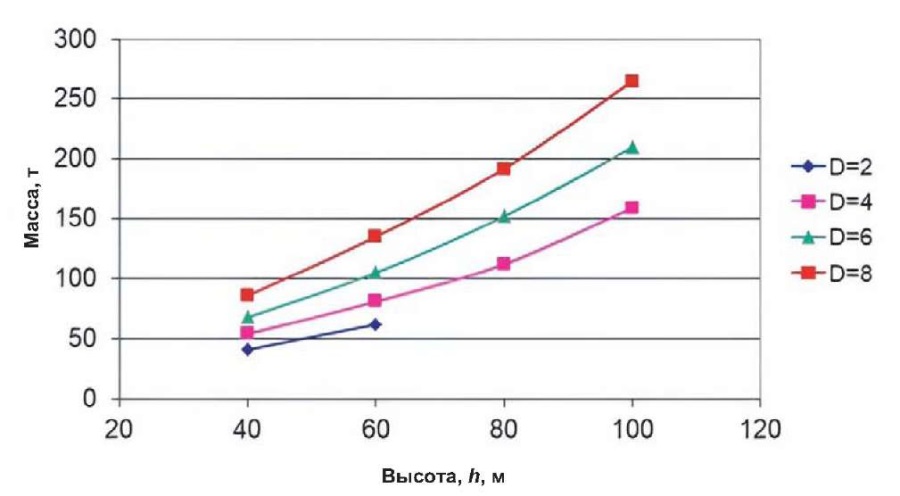
Рис. 16. Изменение массы башни c Turbowind T600–48
Fig. 16. Variations in the mass of a Turbowind T600–48 tower
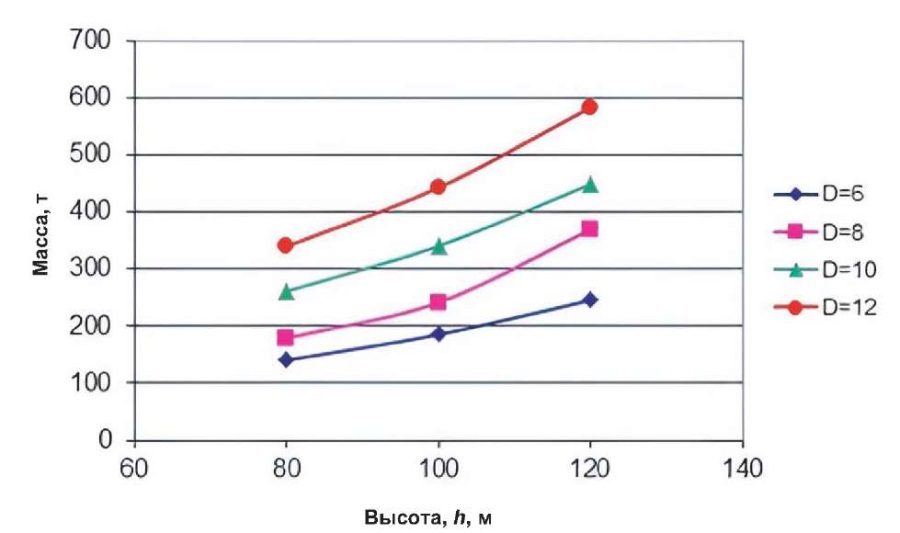
Рис. 17. Изменение массы башни c Eviag EV 100
Fig. 17. Variations in the mass of an Eviag EV 100 tower
Выводы
- При формировании расчетной схемы конусообразной башни в программном комплексе SCAD рационально использовать 44-й тип конечного элемента (4-узловая пластина).
- Значение частоты собственных колебаний при использовании типа КЭ 50 значительно отличается от частот, полученных при использовании других типов КЭ. Изменение частоты при использовании типов КЭ 41, 42, 44 не превышает 0,5 %. Однако в дальнейших расчетах будет использоваться тип КЭ 44 как наиболее универсальный. Применение треугольного типа КЭ 42 приведет к увеличению числа элементов и незначительно повлияет на результат.
- Достаточную величину дискретизации расчетной схемы для определения частоты собственных колебаний следует принимать nR= 12, т. к. дальнейшее увеличение значения nR приведет к изменению частоты собственных колебаний менее чем на 1 %.
- Определены фиксированные частоты для ветроагрегата Eviag EV 100, равные 0,275 и 0,825 Гц. Для Turbowind T600-48 определен диапазон резонансных частот по причине наличия переменной частоты вращения ротора: диапазон стартовых частот – от 0,255 до 0,765 Гц, а диапазон максимальных частот – от 0,383 до 1,149 Гц.
- При вариации высот башен с шагом 20 м при D= 2–8 м значение первой собственной частоты снижается нелинейно от 1,86 до 0,23 Гц для ветротурбины Turbowind T600-48 и от 1,11 до 0,25 Гц для ветротурбины Eviag EV 100. На этапе предварительных расчетов башни необходимо сопоставлять собственные частоты с резонансными и при угрозе попадания конструкции в состояние резонанса вносить коррективы в первично принятые размеры с целью ликвидации резонансной угрозы.
Список литературы
1. Басов К.А. ANSYS для конструкторов. Москва: ДМК Пресс; 2019.
2. Рычков С.П. Моделирование конструкций в среде Femap NX Nastarn. Москва: ДМК Пресс; 2013.
3. Теличко В.Г., Злобин С.Ф., Теличко Г.Н. Параметрическое моделирование расчётных схем в среде РПК SAP2000. Тула: Наука; 2017.
4. Zolochevskiy A.A., Becker A.A. Introduction to ABAQUS. Bristol: Business Investor Group; 2018.
5. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. Киев: Сталь; 2002.
6. Маковкин Г.А., Лихачева С.Ю. Применение МКЭ к решению задач механики деформируемого твердого тела. Н. Новгород: ННГАСУ; 2016.
7. Ermakova A.V. Additional Finite Element Method for Analysis of Reinforced Concrete Structures at Limit States. Moscow: ASV; 2012.
8. Барабаш М.С. Компьютерное моделирование процессов жизненного цикла объектов строительства. К.: Сталь; 2014.
9. Godat A., Legeron F., Bazonga D. Stability investigation of local buckling behavior of tubular polygon columns under concentric compression. Thin-Walled Structures. 2012;53:31–140. h ttps://doi.org/10.1016/j.tws.2011.12.013
10. Trahair N.S. Flexural-torsional buckling of structures. London: E & FNSpon; 2003.
11. Garifullin M., Trubina D., Vatin N. Local Buckling of Cold-Formed Steel Members with Edge Stiffened Holes. Applied Mechanics and Materials. 2014;725-726:697–702. https://doi.org/10.4028/www.scientific.net/AMM.725-726.697
12. Gonçalves R. Camotim D. Elastic buckling of uniformly compressed thin-walled regular polygonal tubes. Thin-Walled Structures. 2013;71:35–45. https://doi.org/10.1016/j.tws.2013.04.016
13. Godat A., Legeron F., Bazonga D. Stability investigation of local buckling behavior of tubular polygon columns under concentric compression. Thin-Walled Structures. 2012;53:131–140. https://doi.org/10.1016/j.tws.2011.12.013
14. Васылев В.Н., Гаранжа И.М. Особенности построения расчетной конечно-элементной модели многогранных гнутых стоек в программно-вычислительном комплексе SCAD Office. Металлические конструкции. 2009;15(2):133–140.
15. Гордиевский Е.М., Мирошниченко А.А., Кулганатов А.З., Соломин Е.В., Станчаускас В.И. Имитационное моделирование ветроэнергетической установки в программе Matlab/Simulink. Известия ВУЗОВ. Северо-Кавказский регион. Технические науки. 2020;(1):25–32. https://doi.org/10.17213/1560-3644-2020-1-25-32
16. Alvare z-Anton L., Koob M., Diaz J., Minnert J. Optimization of a hybrid tower for onshore wind turbines by Building Information Modeling and prefabrication techniques. Vizualization in Engineering. 2016;4:3. https://doi.org/10.1186/s40327-015-0032-4
17. Горохов Е.В., Васылев В.Н., Кузнецов С.Г., Гаранжа И.М., Лозинский Э.А., Щербонос А.Г., Павловский Р.Н. Методика определения геометрических параметров конструкций свободностоящих многогранных стоек с учетом регулирования собственных и вынужденных колебаний. Металлические конструкции. 2012;18(2):85–96.
18. Перельмутер А.В., Микитаренко М.А. Башни для ветроэнергетических установок: тенденции развития. Вестник ДонНАСА. 2014;(5):8–13.
19. Wang L., Kolios A.J., Luengo M.M., Liu X. Structural optimization of wind turbine towers based on finite element analysis and genetic algorithm. Wind Energy Science. 2016;41. https://doi.org/10.5194/wes-2016-41
20. Kudelin A., Kucherov V. Wind ENERGY in Russia: The current state and development trends. Energy Strategy Reviews. 2021;34:100627. https://doi.org/10.1016/j.esr.2021.100627
21. Lu X., McElroy M.B. Global potential for wind-generated electricity. Wind Energy Onshore Offshore Wind Turbines. 2017;(11):51–73. https://doi.org/10.1016/B978-0-12-809451-8.00004-7
22. Жаворонок А.В., Харченко У.А. Проблемы развития ветроэнергетической отрасли на примере России и стран Европы. Современные научные исследования и инновации. 2015;(7):106–110.
23. Афанасьев А.А., Баранов Н.Н. Мировая энергетика: глобальные проблемы и перспективы развития. Энергия: экономика, техника, экология. 2021;(4):34–48. https://doi.org/10.7868/S0233361921040054
24. Фоменко Н.Е., Удовиков А.К., Манаенко И.Н., Фоменко Л.Н. Опыт применения электроразведочных методов для оценки экологической безопасности строительства ветроэнергетических установок в Восточном Донбассе. Инженерный вестник Дона. 2020;(1). Режим доступа: http://www.ivdon.ru/ru/magazine/archive/N1y2020/6270
25. Некрасов Ю.П. Динамические воздействия ветра на металлические решетчатые башни ветроэнергетических установок [диссертация]. Макеевка: ДонГАСА; 2002.
Об авторах
И. М. ГаранжаРоссия
Игорь Михайлович Гаранжа, канд. техн. наук, доцент, доцент кафедры металлических и деревянных конструкций
тел.: +7 (926) 284-55-17
Ярославское шоссе, д. 26, г. Москва, 129337, Российская Федерация
А. В. Танасогло
Россия
Антон Владимирович Танасогло, канд. техн. наук, доцент, доцент кафедры металлических и деревянных конструкций
тел.: +7 (915) 544-36-23
Ярославское шоссе, д. 26, г. Москва, 129337, Российская Федерация
М. М. Писарева
Россия
Милена Михайловна Писарева, студент кафедры металлических и деревянных конструкций
тел.: +7 (985) 906-51-93
Ярославское шоссе, д. 26, г. Москва, 129337, Российская Федерация
Рецензия
Для цитирования:
Гаранжа И.М., Танасогло А.В., Писарева М.М. Особенности построения конечно-элементной расчетной модели трубчатой башни ветроагрегата. Вестник НИЦ «Строительство». 2023;39(4):7-27. https://doi.org/10.37538/2224-9494-2023-4(39)-7-27. EDN: HFKNZG
For citation:
Garanzha I.M., Tanasoglo A.V., Pisareva M.M. Features of a finite-element modeling of a tubular tower for a wind-power unit. Bulletin of Science and Research Center of Construction. 2023;39(4):7-27. (In Russ.) https://doi.org/10.37538/2224-9494-2023-4(39)-7-27. EDN: HFKNZG