Содержание
Перейти к:
Вариативность оценки прочности и жесткости для непрофильных балочных конструкций
https://doi.org/10.37538/2224-9494-2024-2(41)-79-85
EDN: MHYGBD
Аннотация
Введение. Традиционные пути повышения конструкционной прочности и жесткости балок в настоящее время практически исчерпаны, и оптимизация технологий производства и эксплуатации вероятнее всего находится на сочетании применения новых материалов и повышения их надежности как несущих элементов сложного геометрического профиля.
Несущие элементы строительных конструкций работают в условиях высоких нагрузок и, даже несмотря на их преимущественно статический характер, могут испытывать сложное объемное напряженно-деформированное состояние, что не всегда удается подтвердить эмпирическим и статистическим путями.
Цель настоящей статьи состоит в предложении одного подхода оценки прочности и жесткости балочных конструкций, работающих в условиях поперечного изгиба сложного геометрического профиля.
Материалы и методы. Для оценки прочности и жесткости непрофильных балочных конструкций используются классические энергетические приемы расчета прочности и жесткости Кастильяно, Максвелла – Мора или Верещагина (метод моментных площадей), начальных параметров, дифференциальных уравнений изогнутой оси балки.
Результаты. В ходе решения таких задач используются критерии подобия (сглаживания, согласования) Мизеса – Генки и Журкова, хорошо отражающие работу хрупкого или пластичного материала балки. И эти характеристики предлагается объединить в функции долговечности Журкова – Аррениуса.
Выводы. Приведенные в расчетах зависимости можно рекомендовать при проектировании в рамках улучшения изгибной статической и усталостной прочности, а также жесткости несущих элементов строительных конструкций.
Ключевые слова
прочность,
жесткость,
надежность,
непрофильные статически определимые и неопределимые балочные конструкции,
энергетические методы,
критерии подобия
Для цитирования:
Кулагин А.В. Вариативность оценки прочности и жесткости для непрофильных балочных конструкций. Вестник НИЦ «Строительство». 2024;41(2):79-85. https://doi.org/10.37538/2224-9494-2024-2(41)-79-85. EDN: MHYGBD
For citation:
Kulagin A.V. Variability of strength and stiffness assessment for non-profile beam structures. Bulletin of Science and Research Center of Construction. 2024;41(2):79-85. (In Russ.) https://doi.org/10.37538/2224-9494-2024-2(41)-79-85. EDN: MHYGBD
Задача № 1
Условие задачи. Две консольно-закрепленные балки нагружены силой P. Размеры балок H, B, l. Сравнить значения максимальных прогибов и напряжений.
Решение. В прямоугольной балке наибольшие напряжения возникают в сечении у заделки (рис. 1).
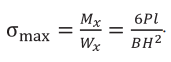
В треугольной балке (рис. 1) осевой момент сопротивления изгибу определится по формуле
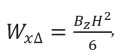
где переменная ширина сечения будет меняться по закону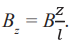 
В сечении, находящемся на расстоянии z от силы P, напряжение найдется по формуле
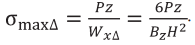
Максимальный прогиб балки на свободном торце определяется с помощью интеграла Мора
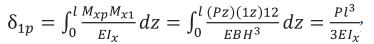
где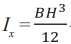 
– осевой момент инерции сечения прямоугольной балки.
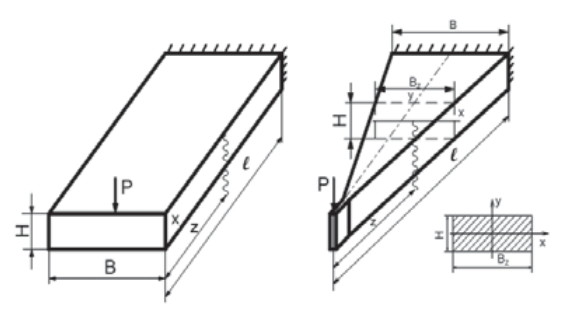
Рис. 1. Прямоугольная и треугольная балки, нагруженные силой Р
Fig. 1. Rectangular and triangular beams loaded with force P
Максимальный прогиб треугольной балки определим с использованием тех же эпюр моментов, как и для балки прямоугольной (рис. 2)
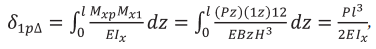
где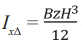 
– осевой момент инерции сечения треугольной балки.
Составим соотношение прогибов и напряжений:
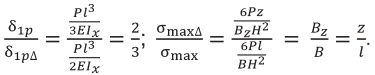
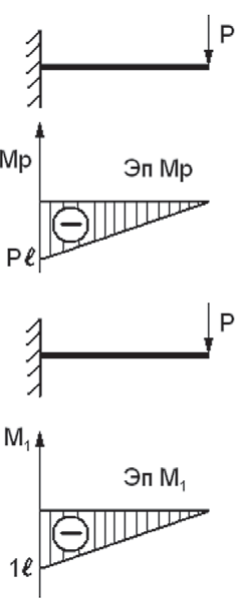
Рис. 2. Схема определения максимального прогиба с помощью интеграла Мора
Fig. 2. Scheme for determining the maximum deflection using the Mohr integral
Задача № 2
Условие задачи. Конструкция состоит из балок одинаковой жесткости EI = const, нагружена силой P, длиной: AB = 3l и CD = 4l. Построить эпюры изгибающих моментов (рис. 3).
Решение. Задача статически неопределимая. Примем за неизвестное усилие X (рис. 4). Перемножим способом Верещагина эпюры изгибающих моментов для балки AB и для балки CD, получим перемещения общего для двух балок сечения B:
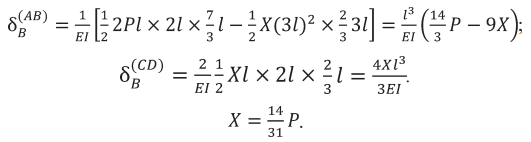
Эпюры изгибающих моментов с найденным значением Х показаны на риc. 4.
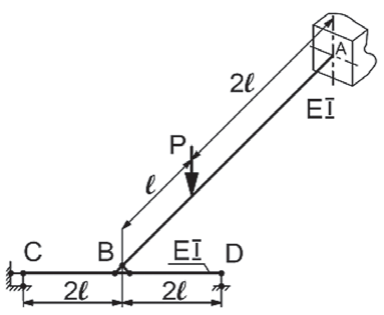
Рис. 3. Конструкция, состоящая из двух жестко соединенных балок одинаковой жесткости
Fig. 3. Structure consisting of two rigidly connected beams of equal stiffness
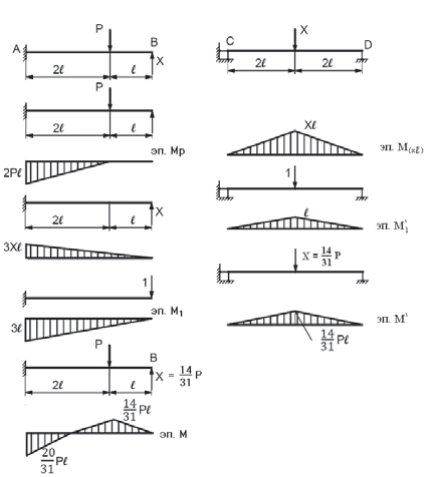
Рис. 4. Эпюры изгибающих моментов, построенные в соответствии с найденным значением Х
Fig. 4. Diagrams of bending moments plotted according to the found value X
Задача № 3
Условие задачи. Брус поперечного сечения 2с × 2с нагружен вертикальной силой P на свободном торце. Длина бруса l. По длине сечения бруса выполнены два отверстия с размерами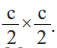 
Определить максимальное напряжение в брусе (рис. 5).
Решение. Моменты инерции относительно главных осей x и y поперечного сечения бруса (рис. 5) определятся по формулам
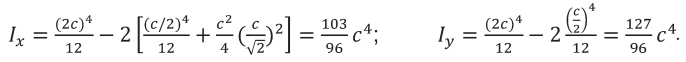
Изгибающие моменты в опасном сечении у заделки относительно этих осей
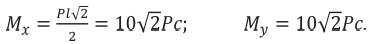
Уравнение нейтральной линии выглядит так
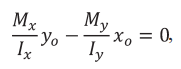
где xo и yo – координаты нейтральной линии сечения бруса.
Опасные точки будут в точках К1 и К2 от нейтральной линии (рис. 6). Напряжения σК1 и σК2 равны
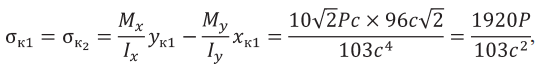
где xк1 и yк1 расстояния наиболее удаленной точки К1 до нейтральной линии.
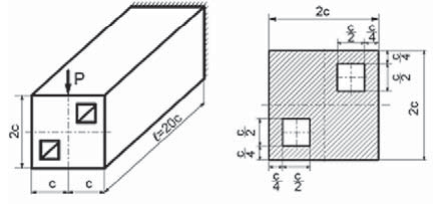
Рис. 5. Расчетная схема бруса с двумя кососимметричными квадратными отверстиями
Fig. 5. Design diagram of a beam with two antisymmetric square holes
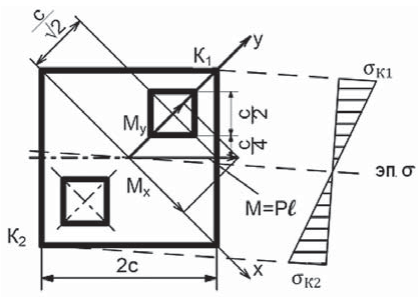
Рис. 6. Наиболее опасные точки и эпюра нормальных напряжений
Fig. 6. The most dangerous points and normal stress distribution diagram
Заключение. Непрофильность рассмотренных балочных систем заключается в особенности исследования геометрии и приложения нагрузок при поперечном изгибе [1–15].
Вариативность перемещений и напряжений учитывается функцией долговечности Журкова – Аррениуса в виде температурно-временной зависимости [2][3].
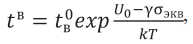
где параметры tВ – текущее время процесса (подстановка напряжений или перемещений вместо tВ) и – константа среды, не зависящая от температуры, заменяются на начальные напряжения или перемещения;
U0 – γσэкв – энергия активации процесса разрушения балки;
k – постоянная Больцмана;
T – температура окружающей среды;
γ – показатель локальных повреждений балки.
Основная характеристика работы непрофильной балки по критерию Мизеса – Генки, согласно теории удельной энергии формоизменения, представляет собой эквивалентное (опасное) напряжение
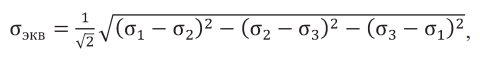
где σ1, σ2, σ3 – наибольшее растягивающее, среднее и наибольшее сжимающее главные напряжения.
Представленные расчеты рекомендуется использовать при проектировании колонн и стен к модульным разбивочным осям, сквозным ригелям рам, подкрановым траверсам и фермам.
Список литературы
1. <i>Тимошенко С.П., Гере Дж.</i> Механика материалов. Санкт Петербург: Издательство «Лань»; 2002.
2. <i>Бабкин А.В., Селиванов В.В.</i> Основы механики сплошных сред. T. 1. Прикладная механика сплошных сред. Москва: Издательство МГТУ им. Н.Э. Баумана; 2006.
3. <i>Селиванов В.В.</i> Механика разрушения деформируемого тела. T. 2. Прикладная механика сплошных сред. Москва: Издательство МГТУ им. Н.Э. Баумана; 1999.
4. <i>Ананьин М.Ю.</i> Основы архитектуры и строительных конструкций. Термины и определения. Екатеринбург: Издательство Уральского Федерального университета; 2016.
5. <i>Зайцев Ю.В., Окольникова Г.Э., Доркин В.В.</i> Механика разрушения для строителей. Москва: ИНФРА-М; 2018.
6. <i>Келлер И.Э., Петухов Д.С.</i> Критерии прочности и пластичности. Пермь: Издательство Пермского национального исследовательского политехнического университета; 2020.
7. <i>Порошин В.Б.</i> Конструкционная прочность. Челябинск: Издательский центр ЮУрГУ; 2019.
8. <i>Атапин В.Г.</i> Сопротивление материалов. Москва: Издательство Юрайт; 2020.
9. <i>Альбакасов А.И., Кудина Л.И., Гаврилов А.А.</i> Строительная механика. Часть I. Статически определимые системы. Оренбург: Издательство Оренбургского государственного университета; 2018.
10. <i>Холодарь Б.Г.</i> Изгиб стержня с произвольной диаграммой деформирования материала. В: Сборник научных статей кафедры «Сопротивление материалов и теоретическая механика». Брест: Издательство Брестского политехнического института; 1994, с. 45–50.
11. <i>Рочняк О.А., Гашко В.И.</i> К вопросу о механизме сопротивления предварительно напряженных железобетонных балок, работающих с двузначной эпюрой изгибающих моментов, действию изгиба с поперечной силой. В: Сборник научных статей кафедры «Сопротивление материалов и теоретическая механика». Брест: Издательство Брестского политехнического института; 1994, с. 121–125.
12. <i>Davidson D.L., Lankford J.</i> Fatigue crack growth in metals and alloys: mechanisms and micromechanics. International Materials Reviews. 1992;37(2):45–76. https://doi.org/10.1179/imr.1992.37.1.45
13. <i>Дородов П.В., Кулагин А.В.</i> О запасе прочности и оценке надежности узлов металлоконструкций. Инженерный вестник Дона [интернет]. 2012;(2):420–423. Режим доступа: http://www.ivdon.ru/uploads/article/pdf/2012_2_66.pdf_810.pdf (дата доступа 01.06.2024).
14. <i>Звездов А.И., Ведяков И.И., Соловьев Д.В.</i> Развитие нормативных подходов по анализу риска прогрессирующего обрушения. Промышленное и гражданское строительство. 2023;(10):34–40. https://doi.org/10.33622/0869-7019.2023.10.34-40
15. <i>Федорова Н.В., Савин С.Ю.</i> Анализ особенностей сопротивления прогрессирующему обрушению конструктивных систем зданий и сооружений при внезапных структурных перестройках: аналитический обзор научных исследований. Строительство и реконструкция. 2021;(3):76–108. https://doi.org/10.33979/2073-7416-2021-95-3-76-108
Об авторе
А. В. Кулагин
ФГБОУ ВО «Удмуртский государственный университет» (УдГУ)
Россия
Россия
Андрей Владимирович Кулагин, канд. техн. наук, доцент кафедры «Защита в чрезвычайных ситуациях
и управление рисками», Институт гражданской защиты
Университетская ул., д. 1, г. Ижевск, 426034, Российская Федерация
e-mail: rekfuby2@rambler.ru
Рецензия
Для цитирования:
Кулагин А.В. Вариативность оценки прочности и жесткости для непрофильных балочных конструкций. Вестник НИЦ «Строительство». 2024;41(2):79-85. https://doi.org/10.37538/2224-9494-2024-2(41)-79-85. EDN: MHYGBD
For citation:
Kulagin A.V. Variability of strength and stiffness assessment for non-profile beam structures. Bulletin of Science and Research Center of Construction. 2024;41(2):79-85. (In Russ.) https://doi.org/10.37538/2224-9494-2024-2(41)-79-85. EDN: MHYGBD
Просмотров:
197
Послать статью по эл. почте 