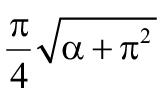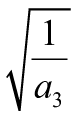Перейти к:
Развитие инженерной методики расчета устойчивости плоской формы изгиба двутавровой балки
https://doi.org/10.37538/2224-9494-2025-3(46)-22-42
EDN: FKKCEI
Аннотация
Введение. Нет сомнений в том, что методика расчета устойчивости плоской формы изгиба балки является одним из самых слабых мест в текущем своде правил по стальным конструкциям. Из-за ограничений метода результаты расчета часто не согласуются с численными расчетами и исследованиями. Нормативный метод расчета основан на трехфакторной формуле и позволяет рассчитывать только простые случаи. В то время как применение стальных зданий для различных нужд растет, нормы проектирования отстают от сегодняшних потребностей и часто оказываются неспособными следовать за расчетами и давать достаточные ответы на вопросы. Как кажется, причина кроется в том, что в области теории устойчивости нет современных разработок. Мы никак не пересматриваем наши предыдущие результаты и даже не пытаемся улучшить текущую теорию. А в случае с теорией балок похоже, что мы завели ее в тупик.
Цель. Создание современного подхода в разрешении вопроса изгибно-крутильной потери устойчивости балки. Создание единого уравнения коэффициента устойчивости при изгибе.
Материалы и методы. Переработка бифуркационной задачи по теории В.З. Власова для тонкостенных стержней и разработка формулы в деформационной теории на основании формулы Мерчанта, показательной и степенной функций.
Результаты. По результатам работы предлагается усовершенствованная методика расчета устойчивости плоской формы изгиба балки, а также новый набор коэффициентов и уравнений для решения задачи. Предложенные решения дополняют и расширяют СП 16.13330.2017.
Выводы. Показывается возможность расширения методов и норм расчета стальных конструкций в части общей устойчивости балок.
Ключевые слова
Для цитирования:
Ильюшенков А.О. Развитие инженерной методики расчета устойчивости плоской формы изгиба двутавровой балки. Вестник НИЦ «Строительство». 2025;46(3):22-42. https://doi.org/10.37538/2224-9494-2025-3(46)-22-42. EDN: FKKCEI
For citation:
Ilyushenkov A.O. Development of engineering methodology for calculating the plane bending stability of an I-beam. Bulletin of Science and Research Center of Construction. 2025;46(3):22-42. (In Russ.) https://doi.org/10.37538/2224-9494-2025-3(46)-22-42. EDN: FKKCEI
Введение
Техническая теория пространственной устойчивости тонкостенного стержня открытого профиля постоянного сечения была изложена в трудах В.З. Власова [1] в 50-х годах прошлого столетия. Для того чтобы составить понимание, что заключено в сегодняшних нормах по стальному строительству в отношении расчета балок на общую устойчивость, достаточно изучить книгу Б.М. Броуде [2]. Справочную информацию, способствующую пониманию методов решения задач устойчивости, можно найти в книге [3]. Расчет балки на общую устойчивость осуществляется по бифуркационной теории по «трехфакторной формуле». Для вычисления изгибно-крутильного критического момента требуется определить три числовых коэффициента. Каждому виду и месту приложения поперечной нагрузки по длине балки и высоте поперечного сечения определен свой набор коэффициентов. Настоящие нормы по стальным конструкциям [4] содержат достаточно ограниченную инженерную методику расчета устойчивости плоской формы изгиба балки. Остающаяся неизменной со времени публикации книги Б.М. Броуде, методика не различает комбинационного приложения поперечных нагрузок к балке, как и действий разных концевых изгибающих моментов. А наличие уравнений аппроксимационных кривых изгибно-крутильной характеристики балки ψ(α) только усугубляет статус методики, так как требует индивидуальной формулы ψ(α) для каждого случая. В связи с этим требуется пересмотреть классическое решение и продемонстрировать иной путь решения задачи.
Постановка задачи
За основу в разрешении проблемы устойчивости плоской формы изгиба балки двутаврового симметричного сечения принимаем дифференциальное уравнение равновесия:
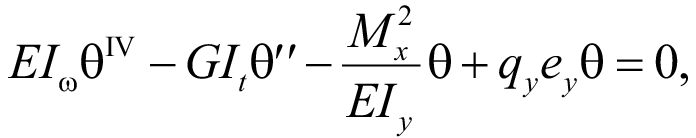 (1)
(1)
где EIω – секториальная жесткость (жесткость при депланации);
GIt – жесткость при кручении;
EIy – изгибная жесткость из плоскости действия изгибающего момента Mx;
ey – расстояние по высоте балки от центра тяжести совпадающего с центром изгиба до точки приложения поперечной нагрузки;
Mx – изгибающий момент от внешней поперечной нагрузки, действующий на длине балки l в точке z;
qy – интенсивность нагрузки.
Мы будем следовать организации и традициям свода правил по стальным конструкциям [4][5] и получим конечные формулировки в удовлетворяющей форме записи документа СП 16.13330.2017. В разработке инженерной методики будет полезен справочник интегралов [6], а также идеи и мысли, изложенные в книге П.И. Алексеева [7].
Решение осуществляем в безразмерной форме.
Длина балки в безразмерной форме:
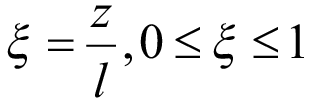 . (2)
. (2)
Первая и вторая производные ξ:
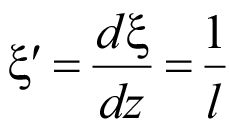 , (3)
, (3)
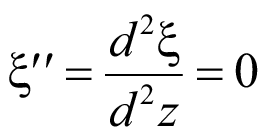 . (4)
. (4)
Безразмерный параметр для изгибающего момента mb:
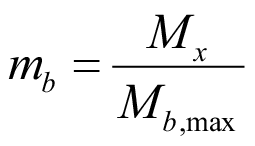 , (5)
, (5)
где Mb,max – максимальный балочный изгибающий момент.
Первая производная mb (5) по dz дает поперечную силу:
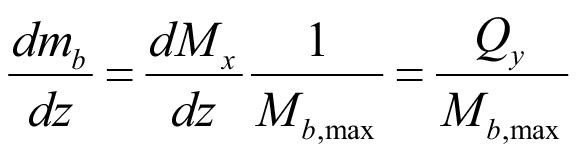 . (6)
. (6)
Первая производная mb по dξ с учетом (3):
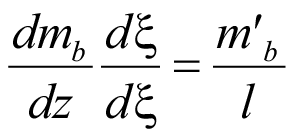 . (7)
. (7)
Вторая производная mb (5) по dz дает равномерно распределенную нагрузку:
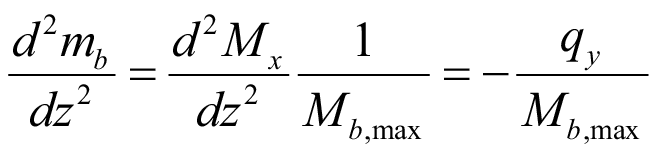 . (8)
. (8)
Вторая производная mb по dξ с учетом (4):
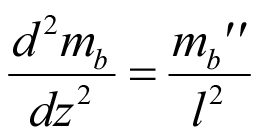 . (9)
. (9)
Приравнивая (8) и (9), выражаем равномерно распределенную нагрузку:
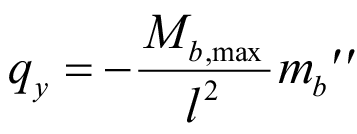 . (10)
. (10)
Для разрешения дифференциального уравнения (1) применяем аналитический метод Бубнова – Галеркина. Для шарнирно опертой балки применяется базисная функция в виде ряда синуса:
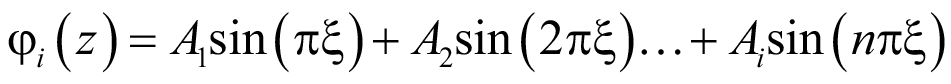 . (11)
. (11)
Удерживая в методе Бубнова – Галеркина только первый член базисной функции синуса (11) и подставляя безразмерные переменные в уравнение равновесия (1), получим интегральное равенство:
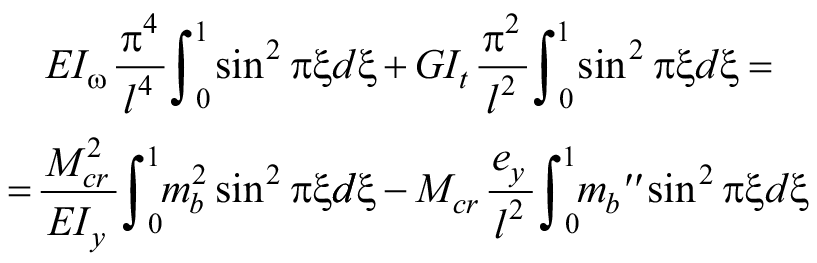 . (12)
. (12)
Решение дифференциального уравнения
Обозначим интегральные выражения, содержащие изгибающий момент, через:
 . (13)
. (13)
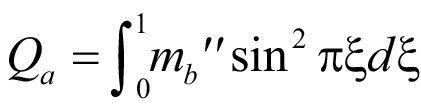 . (14)
. (14)
Интегралы при секториальной и крутильной жесткости решаются таблично [6], поэтому с учетом введенных обозначений (13) и (14) решение (12) в сокращенном виде:
 . (15)
. (15)
Формулировка уравнения упругого критического изгибающего момента
При рассмотрении вопроса устойчивости интересует только положительный корень квадратного уравнения (15):
 . (16)
. (16)
В (16) присутствует эксцентриситет ey, который определяет место приложения поперечной нагрузки по высоте сечения. ey заключен в границы, считая, что центр тяжести и центр изгиба балки – это ноль:
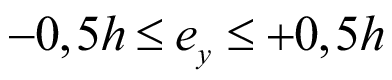 . (17)
. (17)
В безразмерном виде:
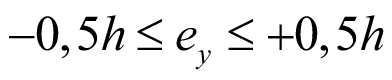 . (18)
. (18)
Вводим безразмерный параметр 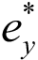 , который обратится в равенство:
, который обратится в равенство:
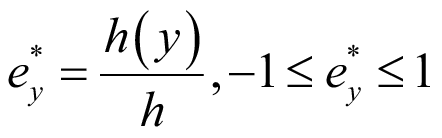 , (19)
, (19)
где h – полная высота двутавра;
h(y) – ордината по высоте поперечного сечения балки, отсчитываемая от центра тяжести, на которой будет приложена поперечная нагрузка, –h ≤ h(y) ≤ +h.
Нормативный параметр изгибно-крутильной характеристики:
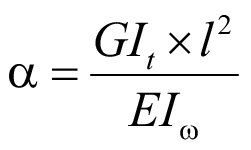 . (20)
. (20)
Преобразуем уравнение (16) с учетом (18) и (20):
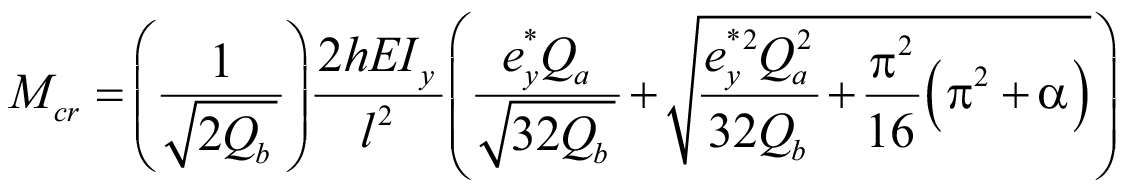 . (21)
. (21)
В (21) выделяем новый изгибно-крутильный параметр балки при чистом изгибе:
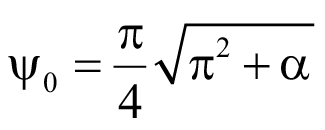 . (22)
. (22)
 . (23)
. (23)
В (23) выделим два коэффициента. Первый коэффициент влияния градиента изгибающего момента:
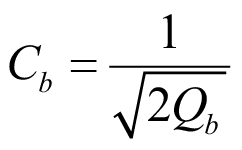 . (24)
. (24)
Второй коэффициент определяет вид поперечной нагрузки взаимоувязанный с 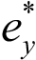 :
:
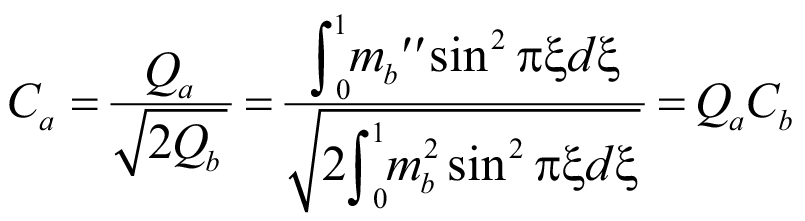 . (25)
. (25)
Инженерная методика расчета устойчивости плоской формы изгиба балки
Расчет на устойчивость изгибаемого элемента сплошного сечения при изгибе в плоскости стенки, совпадающей с плоскостью симметрии сечения, согласно СП 16.13330.2017 [4], производят по формуле:
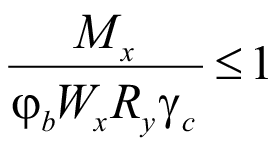 . (26)
. (26)
Критические напряжения для симметричного двутавра:
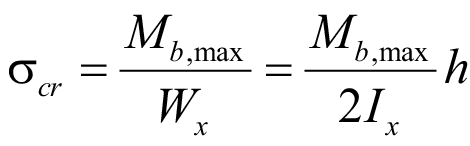 . (27)
. (27)
Коэффициент устойчивости при изгибе φb определяется через напряжения текучести:
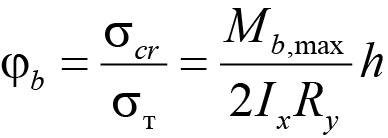 . (28)
. (28)
Подставляем (28) в (23):
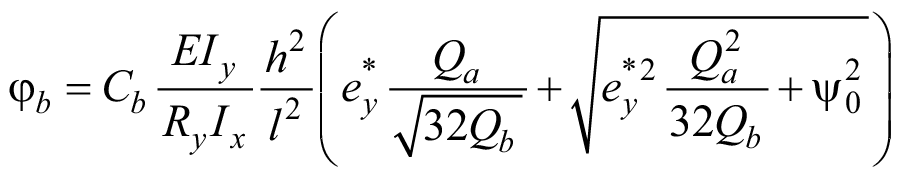 . (29)
. (29)
Из (29) выделяем нормативный параметр ψ:
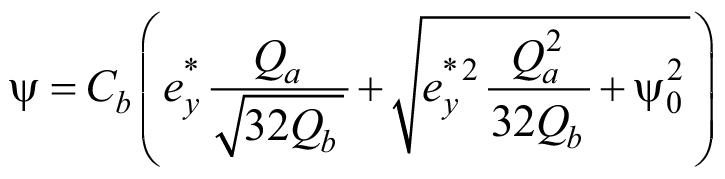 . (30)
. (30)
Квадратный корень в (30) подлежит разложению в степенной ряд:
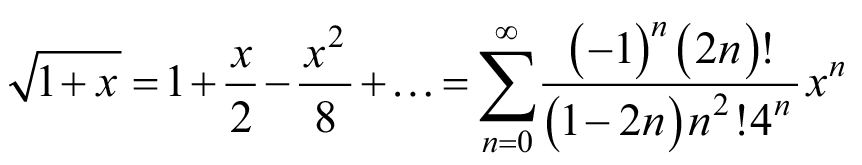 . (31)
. (31)
Ряд (31) ограничиваем удержанием первых двух членов в силу малой поправки последующих членов более высоких порядков:
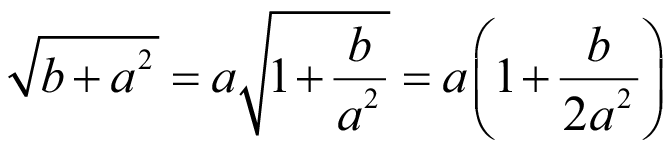 . (32)
. (32)
Тогда (30) с учетом (32) дает:
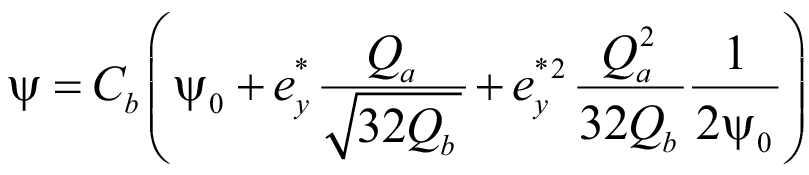 . (33)
. (33)
Или в сокращенной форме:
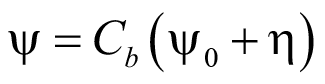 , (34)
, (34)
где Cb – коэффициент, зависящий от вида поперечной нагрузки, по (24);
ψ0 – изгибно-крутильный коэффициент при чистом изгибе по (22);
η – новый обобщенный коэффициент места приложения поперечной нагрузки (35).
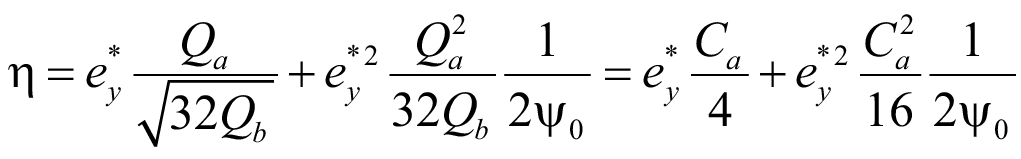 . (35)
. (35)
В (35) по-прежнему присутствует характеристика ψ0. Однако второе слагаемое в целом всегда вносит очень малую поправку и только лишь при α → 0. Коэффициент η можно рассмотреть через верхнюю и нижнюю границы решения.
При α = 0, ψ0 = 0,25 π², поэтому:
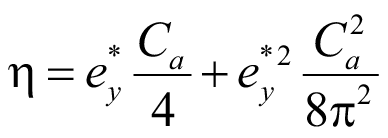 . (36)
. (36)
При α = 400, ψ0 ≈ 16:
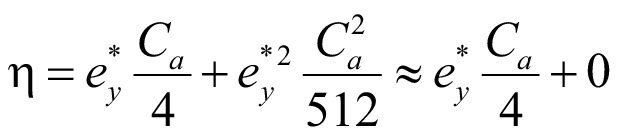 . (37)
. (37)
Уравнение (37) – это нижняя граница коэффициента η, отделенная от изгибно-крутильной части ψ0. Его значение зависит только от второй производной изгибающего момента (25), что делает его простым числом. Его возможно обобщить от множества случаев к одному, что в свою очередь делает уравнение изгибно-крутильного параметра ψ (34) свободным от необходимости иметь таблицы или полиномы, как это существует сейчас в [4]. Коэффициент η можно аппроксимировать и с помощью интерполяционного полинома Лагранжа и Ньютона [3]:
 . (38)
. (38)
При 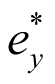 = 0, A0 = 0. Тогда в виде неполного квадратного уравнения:
= 0, A0 = 0. Тогда в виде неполного квадратного уравнения:
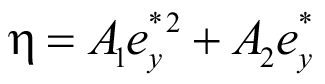 . (39)
. (39)
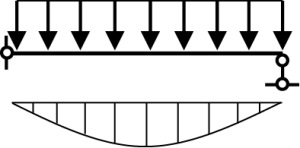
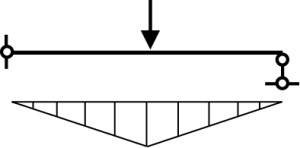
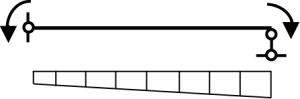
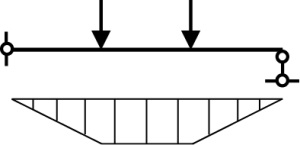
Будем рассматривать шарнирно опертую балку, нагруженную равномерно распределенной нагрузкой и концевыми изгибающими моментами, одновременно. Расчетная схема балки показана на рис. 1а.
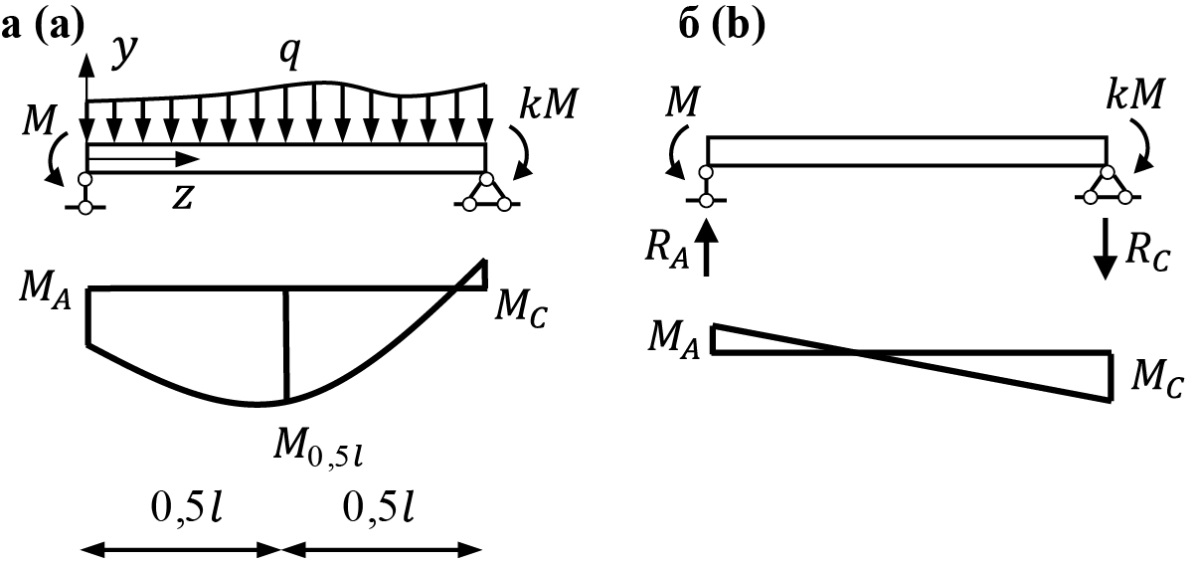
Рис. 1. Шарнирно опертая балка, подверженная действию разных концевых изгибающих моментов и равномерно распределенной нагрузки
Fig. 1. A pinned beam subjected to different end bending moments and a uniformly distributed load
При действии двух внешних нагрузок одновременно безразмерный параметр (5):
 . (40)
. (40)
Изменение изгибающего момента по длине стержня от действия разных концевых изгибающих моментов происходит линейно:
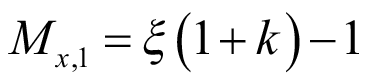 . (41)
. (41)
Закон изменения изгибающего момента от действия равномерно распределенной нагрузки:
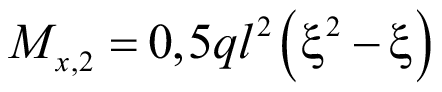 . (42)
. (42)
Максимальный изгибающий момент для Mx,1 находится на одной из опор, поэтому:
Mb1,max = MA. (43)
Максимальный изгибающий момент на середине балки от равномерно распределенной нагрузки:
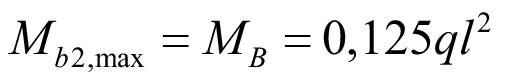 . (44)
. (44)
Подставляем сумму моментов (40) в уравнение градиента изгибающего момента Cb (24):
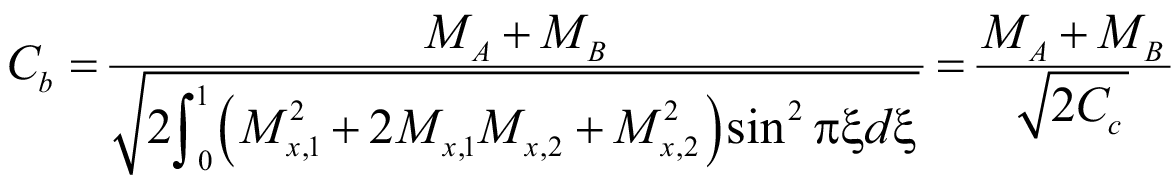 . (45)
. (45)
В знаменателе (45) находится квадрат суммы. Выделяем его отдельно и подставляем (41) и (42):
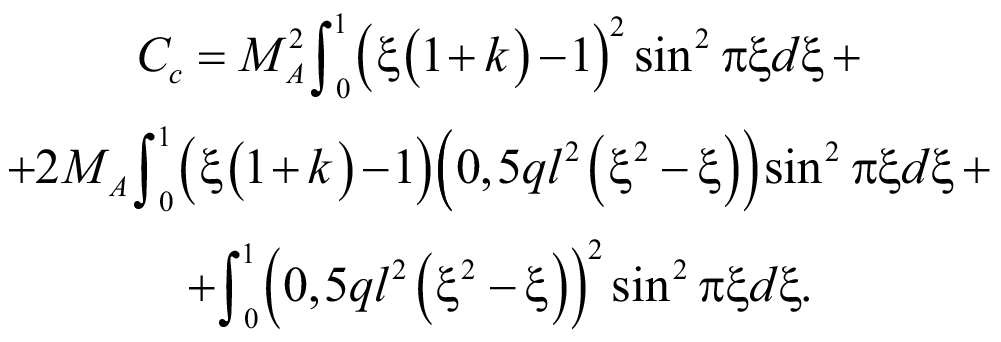 (46)
(46)
Для решения (46) следует использовать свойство дистрибутивности интеграла; понижение степени синуса; интегрирование по частям. Запишем конечный результат интегрирования:
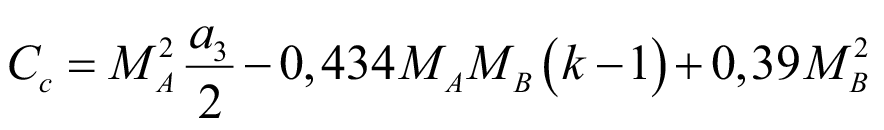 , (47)
, (47)
где
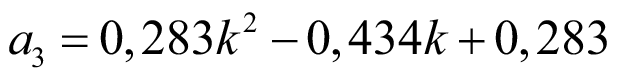 ;
;
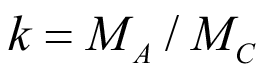 .
.
Подставляем (47) в (45) и находим, что коэффициент влияния градиента момента Cb при действии двух внешних нагрузок одновременно:
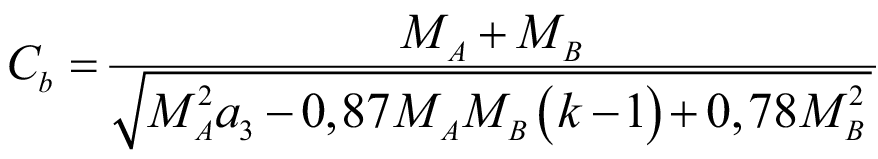 . (48)
. (48)
Если одна из нагрузок в (48) отсутствует, например k = 0, MA = 0, тогда имеет случай только равномерно распределенной нагрузки, для которой существует единственное решение:
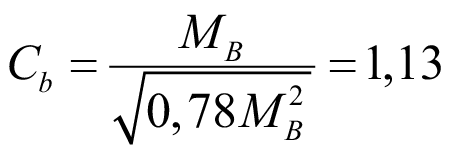 . (49)
. (49)
Для случая, когда балка подвержена только действию концевых изгибающих моментов и MB = 0, либо эпюра изгибающих моментов такова, что она может быть описана линейной зависимостью или имеет пологий и близкий к линейному вид:
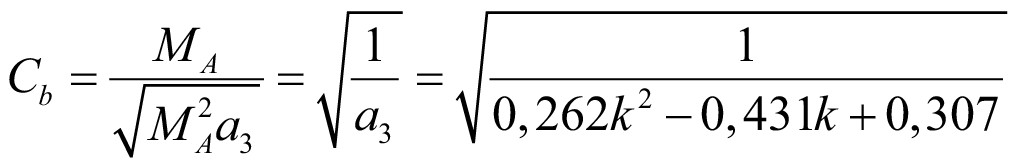 . (50)
. (50)
В формуле (50) приведен уточненный коэффициент α3 [8] при условии удержания большего количества членов ряда синуса (11). Для шарнирно опертой балки в методе Бубнова – Галеркина обычно достаточно удерживать только первый член ряда (11). Погрешность мала при сравнении с численным решением. Но для концевых моментов (41) в области двойной кривизны, когда эпюра изгибающих моментов меняет знаки по длине балки, погрешность составляет 4–5 %. На рис. 2 сплошной линией показана кривая при удержании только первого слагаемого ряда (11). Пунктиром показана точная кривая по (50), полученная методом конечных разностей в работе [8].
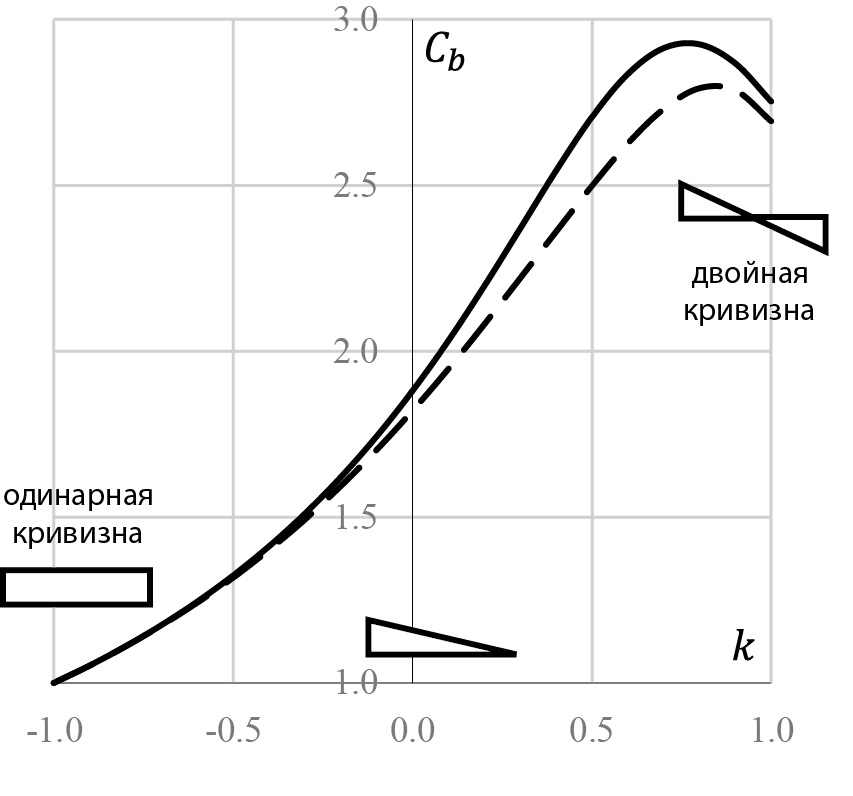
Рис. 2. Приближенная и точная кривая коэффициента Cb при действии разных концевых изгибающих моментов
Fig. 2. Approximate and exact curve of the Cb coefficient under different end bending moments
Когда балка загружена только концевыми изгибающими моментами (рис. 1б), опорная реакция:
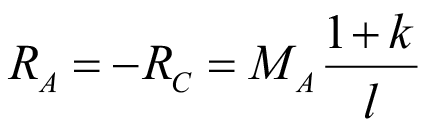 . (51)
. (51)
Тогда изгибающий момент на середине балки:
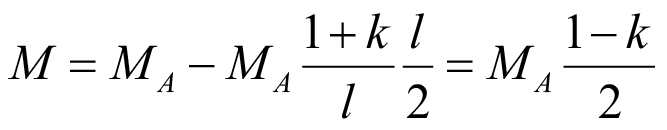 . (52)
. (52)
Изгибающий момент только от равномерно распределенной нагрузки:
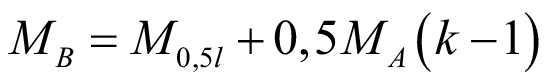 , (53)
, (53)
где M0,5l – изгибающий момент из эпюры моментов по середине балки при действии двух нагрузок одновременно.
Соответственно, отношение моментов MA/MB можно выразить как:
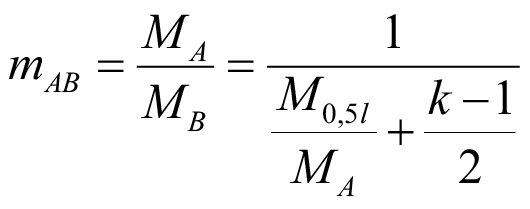 . (54)
. (54)
Используя свойство (54), приходим к обобщенной формуле коэффициента градиента момента в безразмерных величинах (48):
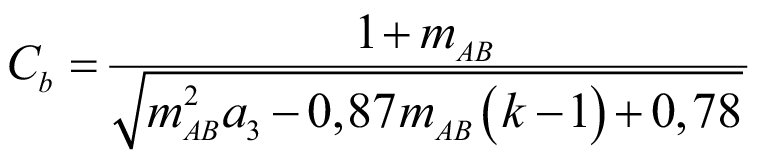 . (55)
. (55)
Уравнение (55) позволяет найти коэффициент Cb, когда эпюра изгибающих моментов имеет криволинейное очертание, как это показано на рис. 1а. Чаще всего этот случай справедлив для балок в рамных каркасах. Если рассматривается комбинация концевых моментов и сосредоточенных сил, уравнение (55) будет иметь числовые коэффициенты немногим ниже. Равномерно распределенная нагрузка образует нижнюю границу результатов. Данную идею можно встретить в книге П.И. Алексеева [7]. Автор рассматривает сложные случаи путем суммирования по формуле (40).
Вторая производная mb суммы двух нагрузок (41) и (42):
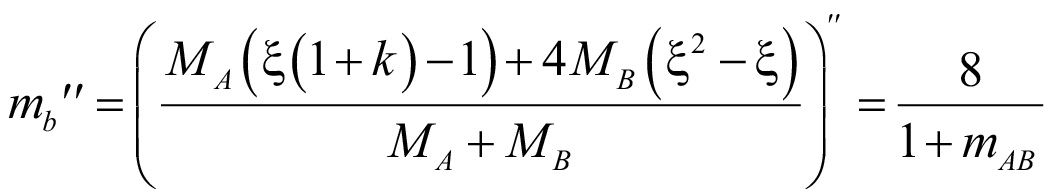 . (56)
. (56)
Подставляя (56) в интегральное выражение (25), находим коэффициент учета места приложения поперечной нагрузки по высоте:
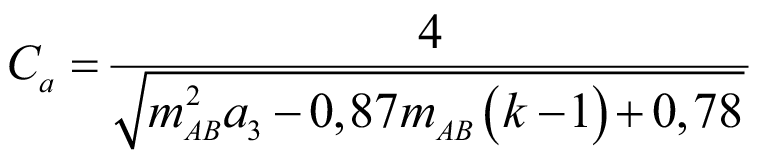 . (57)
. (57)
На сегодняшний день любая из существующих методик не позволяет учитывать влияние места приложения поперечной нагрузки по высоте поперечного сечения балки при одновременном действии нескольких нагрузок. Данный вопрос практически не развит. Учет только одной поперечной нагрузки обычно приводит к занижению результатов, но при этом делает расчет более простым.
Если одна из нагрузок в (57) отсутствует, например k = 0, MA = 0, тогда только для равномерно распределенной нагрузки:
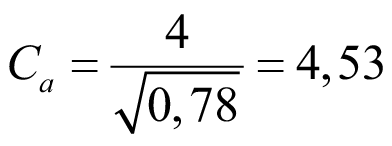 . (58)
. (58)
Очевидно, что при MB = 0:
Ca = 0. (59)
Дальнейшее решение продолжаем с коэффициентом (58). Подставляем значение Ca (58) в уравнение (35):
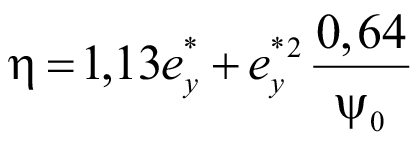 .
.
Изгибно-крутильный коэффициент при действии только равномерно распределенной нагрузки:
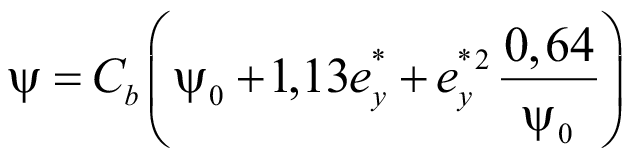 . (60)
. (60)
Если нагрузка прикладывается к верхнему (сжатому) поясу,  = –1:
= –1:
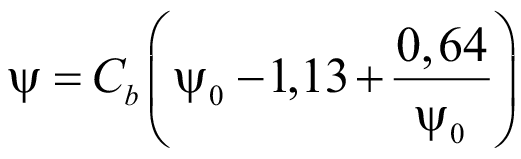 . (61)
. (61)
К нижнему (растянутому) поясу, 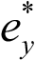 = +1:
= +1:
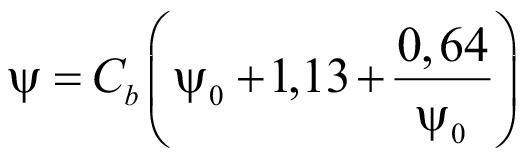 . (62)
. (62)
Для (61) и (62) построим графики зависимости ψ0 – ψ и покажем их на рис. 3. Это прямые отрезки. Что означает возможность аппроксимации (61) и (62) в форме линейного алгебраического уравнения.
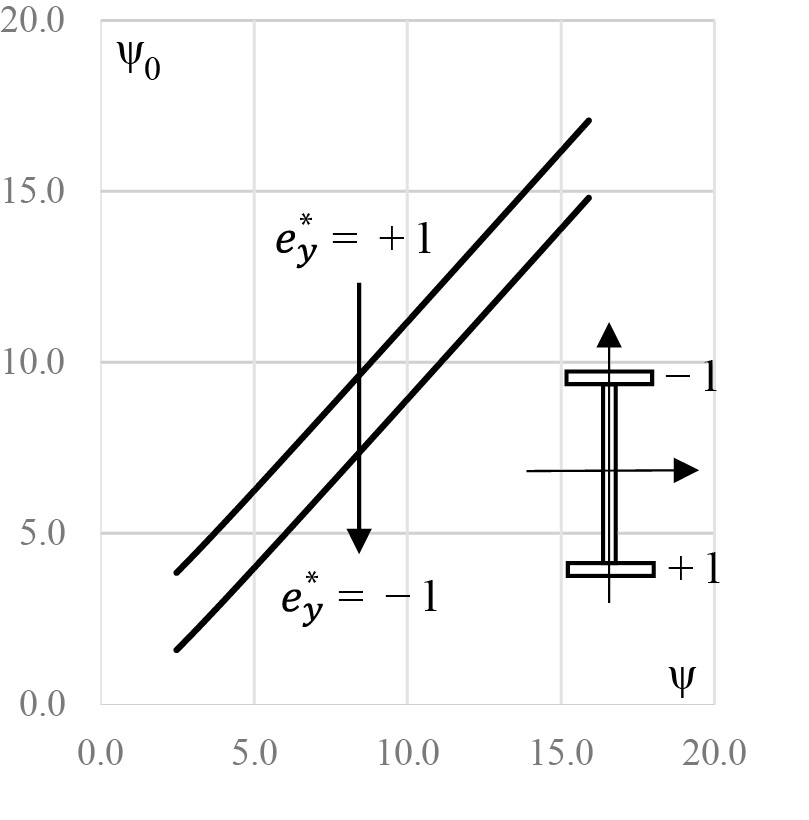
Рис. 3. График зависимости ψ0 – ψ для шарнирно опертой балки при действии равномерно распределенной нагрузки
Fig. 3. Dependence of ψ0 – ψ for a pinned beam under a uniformly distributed load
Аппроксимация по графику, показанному на рис. 3, дает следующие линейные зависимости:
При 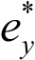 = –1, коэффициент:
= –1, коэффициент:
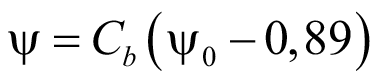 . (63)
. (63)
При 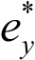 = +1, коэффициент:
= +1, коэффициент:
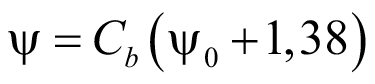 . (64)
. (64)
В уравнении (38) первая точка имеет координаты [ 0,0], A0 = 0. При ey = –1 из (63) следует, –0,89 = –A1 + A2. При ey = +1 из (64) следует, 1,38 = A1 + A2. Устанавливаем, что при действии равномерно распределенной нагрузки коэффициент η:
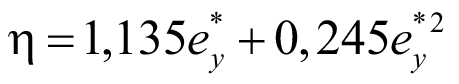 . (65)
. (65)
Уравнение (65) отделено от изгибно-крутильного параметра и в точности определяет поправку изгибно-крутильного состояния балки от места приложения поперечной нагрузки по высоте, а также позволяет находить промежуточные значения по высоте.
Возвращаясь к уравнению (37), линейная зависимость:
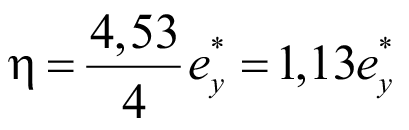 . (66)
. (66)
На графике, показанном на рис. 4а, приведены зависимости η по (65) и (66). Линейная зависимость образует нижнюю границу. Это искажает конечный результат расчета, но делает его настолько простым, что инженеру больше нет необходимости выбирать вид поперечной нагрузки. На рис. 4б показан график с кривыми η по (35) для набора случаев приложения сосредоточенной силы по середине, двух и трех равноудаленных друг от друга сосредоточенных сил. Из этого графика можно заключить, что одно простое уравнение (66) дает возможность выполнить практический расчет и учесть с достоверной точностью влияние места приложения поперечной нагрузки по высоте. Поэтому заключаем, что изгибно-крутильный коэффициент может быть формализован в виде одного уравнения:
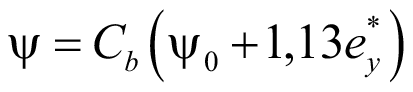 . (67)
. (67)
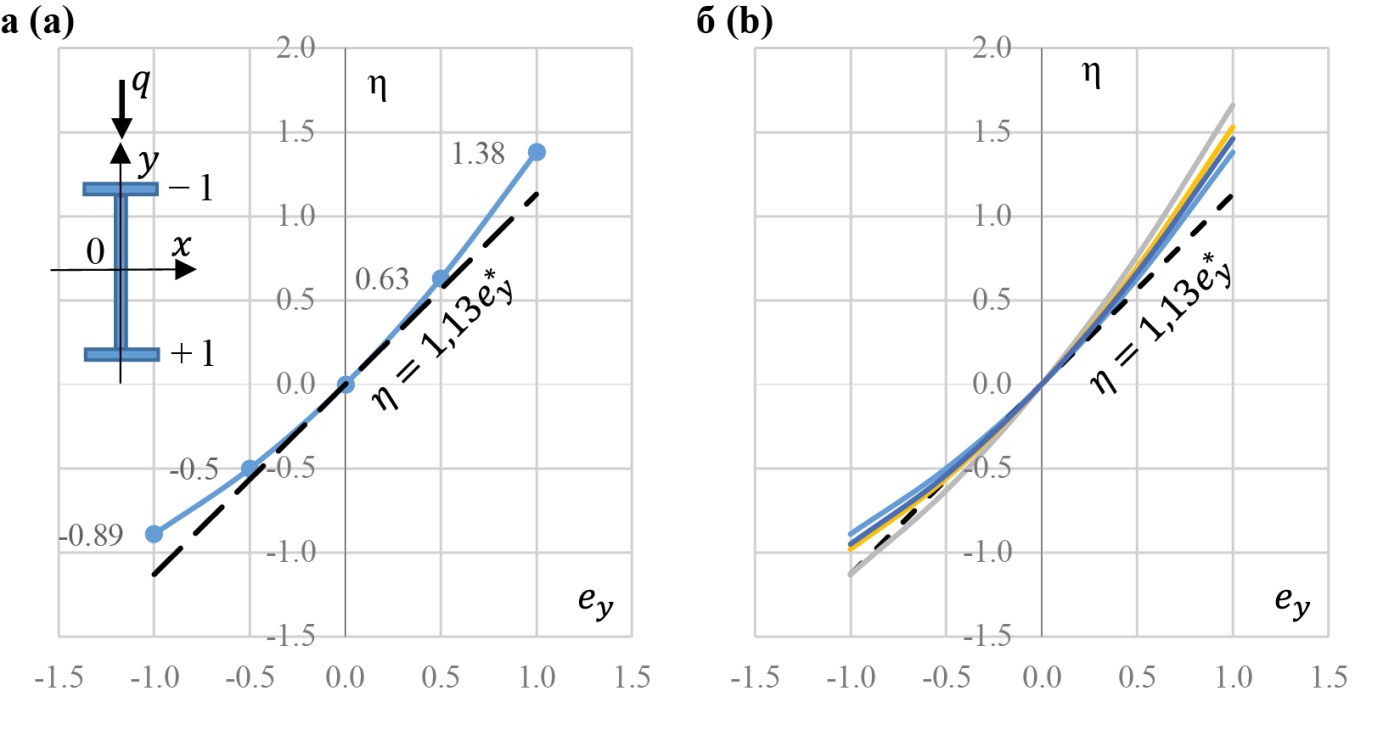
Рис. 4. Графики зависимости ey – η для шарнирно опертой балки при действии равномерно распределенной нагрузки в зависимости от места приложения поперечной нагрузки по высоте сечения балки (а) и набора сосредоточенных сил (б)
Fig. 4. Dependences of ey – η for a pinned beam under a uniformly distributed load depending on the location of transverse load application along the height of the beam section (a) and the set of concentrated forces (b)
В уравнении (67) коэффициент Cb вычисляется по обобщенной формуле (55) либо с помощью табл. 1. По табл. 1 также можно наблюдать насколько близки коэффициенты η.
Таблица 1
Таблица коэффициента ψ для балок двутаврового сечения с двумя осями симметрии
Table 1
Calculation of the ψ coefficient for I-beams with two symmetry axes
Вид нагрузки в пролете | ψ = Cb(ψ0 + η) | ||
ψ0 | Cb | η | |
Равномерно распределенная
|
| 1,13 | 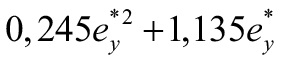 |
Сосредоточенная на середине
| 1,35 | 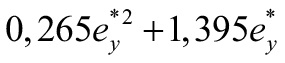 | |
Изгибающие моменты по концам стержня
|
| 0 | |
Две равноудаленные сосредоточенные силы
| 1,08 | 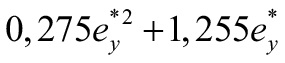 | |
Три равноудаленные сосредоточенные силы
| 1,17 | 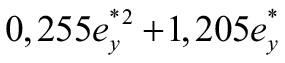 | |
С учетом всего вышеизложенного упругий критический изгибающий момент будет записан в обновленной форме:
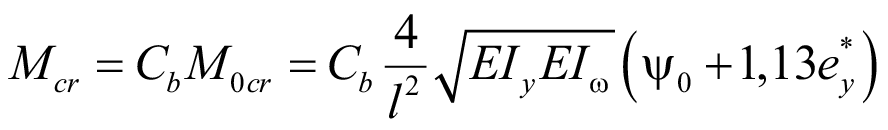 . (68)
. (68)
Деформационный расчет устойчивости плоской формы изгиба балки
Формула Мерчанта является одним из возможных способов решить деформационную задачу устойчивости плоской формы изгиба двутавровой балки. В самом общем смысле расчет по Мерчанту на устойчивость представляется в форме, приведенной из двух линейных систем – линейно-упругой системы и жесткопластической на предельное равновесие. Графически уравнение Мерчанта можно представить в виде треугольника, который показан пунктирной линией на рис. 5. Сплошной кривой линией описывается реальное поведение балки, когда уравнение имеет некоторую степень n. При n = 1 уравнение Мерчанта образует нижнюю и верхние границы, куда заключена реальная кривая со степенью n:
 . (69)
. (69)
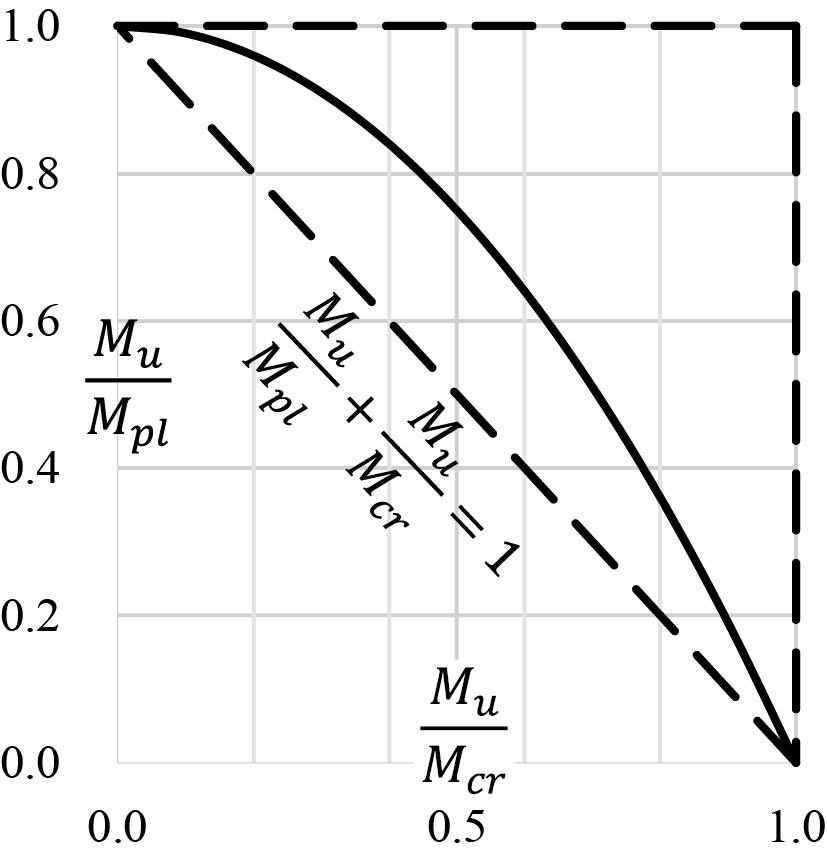
Рис. 5. Графическая интерпретация формулы Мерчанта
Fig. 5. Graphical representation of Merchant’s formula
За предельный изгибающий момент Mu в (69) следует считать величину, получаемую по результатам испытаний от соответствующей ему предельной нагрузки, поэтому в (69) под Mu следует понимать номинальную прочность на изгиб:
Mu = WxRy. (70)
Полный пластический момент Mpl:
Mpl = WplRy. (71)
Упругий изгибно-крутильный момент Mcr,el вычисляется по бифуркационной теории по (68) при чистом изгибе Cb = 1.
Коэффициент устойчивости при изгибе:
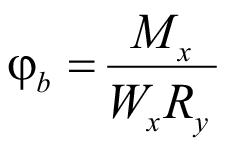 . (72)
. (72)
Изгибно-крутильная условная гибкость:
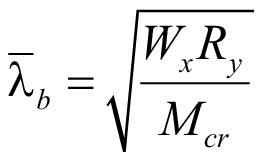 . (73)
. (73)
Используя зависимости 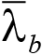 и φb по (72) и (73), формулу Мерчанта (69) можно преобразовать в условие для проверки на общую устойчивость изгибаемого элемента при изгибе в плоскости стенки.
и φb по (72) и (73), формулу Мерчанта (69) можно преобразовать в условие для проверки на общую устойчивость изгибаемого элемента при изгибе в плоскости стенки.
Чтобы учесть фактическую эпюру изгибающего момента, уравнение Мерчанта (69) следует скорректировать путем следующих изменений:
Упругий критический момент:
Mcr,el = CbM0cr,el. (74)
Предельный изгибающий момент:
Mu = CbM0u. (75)
Тогда, подставляя (74) и (75) в (69), получим:
 . (76)
. (76)
Подставляя сокращенные обозначения 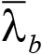 (73) и φb (72), получаем:
(73) и φb (72), получаем:
 . (77)
. (77)
M. Kubo, Y. Fukumoto, Y. Itoh и T. Usami [9–12] провели ряд важных исследований и испытаний над двутавровыми балками с учетом места приложения нагрузки и изменения градиента момента по длине балки. Они обобщили экспериментальные и численные данные испытаний балок (всего 544, 420 из них в Японии) на тот момент времени, к 1996 году. Были созданы кривые зависимости коэффициента устойчивости при изгибе от условной гибкости для прокатных и сварных балок 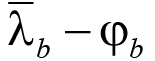 , которые показали несогласованность с существующими предложениями в определении степени n в формуле Мерчанта. На основании статистического анализа было установлено, что нижняя граница кривой коэффициента устойчивости при изгибе должна быть образована со степенью n = 1,5.
, которые показали несогласованность с существующими предложениями в определении степени n в формуле Мерчанта. На основании статистического анализа было установлено, что нижняя граница кривой коэффициента устойчивости при изгибе должна быть образована со степенью n = 1,5.
Вместе с формулой Мерчанта одной из современных и успешных формулировок кривой устойчивости при изгибе следует назвать экспоненциальную (показательную) функцию следующего вида:
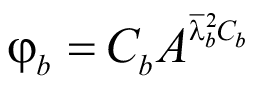 , (78)
, (78)
где A – некоторый подбираемый числовой коэффициент кривой.
Формула (78) была разработана в методе предельных состояний R.H.R. Tide в 1984 году [13] с целью уйти от мультикривых устойчивости колонн к одной кривой, которые были разработаны комитетом стального строительства США и R. Bjorhovde в 60-х годах [14]. На рис. 6 наглядно показано, как показательная зависимость (78) способна описать кривую устойчивости в области средней и малой гибкостей.
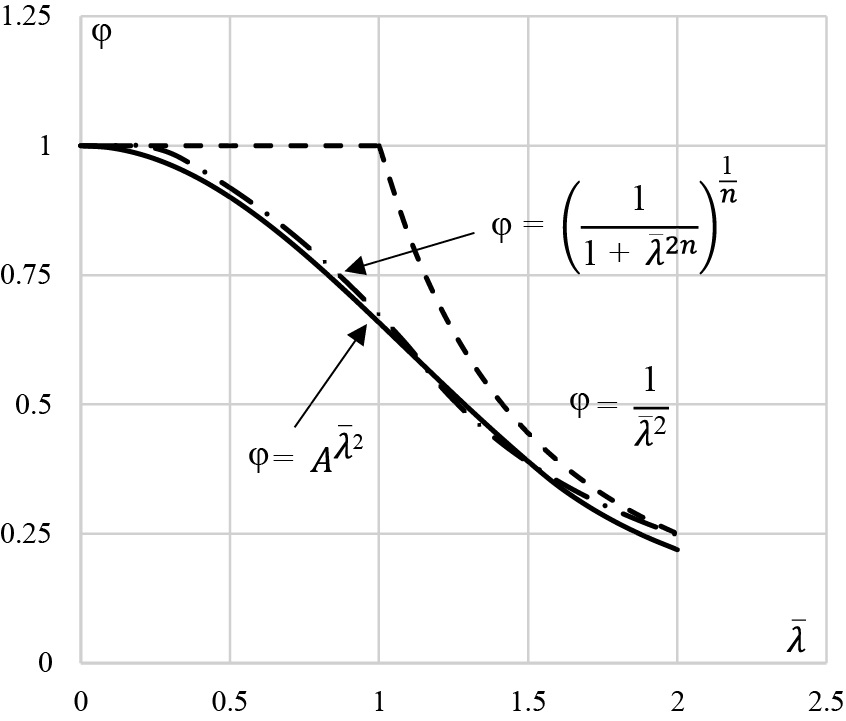
Рис. 6. График зависимости 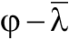 коэффициента продольного изгиба от условной гибкости в экспоненциальной и степенной формах записей
коэффициента продольного изгиба от условной гибкости в экспоненциальной и степенной формах записей
Fig. 6. Relationship between the 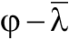 longitudinal bending coefficient and the conditional flexibility in exponential and degree forms of the records
longitudinal bending coefficient and the conditional flexibility in exponential and degree forms of the records
Редукционный коэффициент в прямом методе расчета конструкций
Нормы США по стальному строительству ANSI/AISC 360-22 [15] уже некоторое время практикуют метод прямого анализа. В этом методе расчета стальных конструкций изгибная жесткость элементов, в зависимости от напряженного состояния, напрямую модифицируется коэффициентом редукции. Всего существует две модели коэффициента редукции. Первый коэффициент редукции, обозначаемый через τb, считается по бифуркационной теории в методе по допустимым напряжениям и включает в себя остаточные напряжения. Геометрическое несовершенство учитывается путем умножения на дополнительный понижающий коэффициент точно так же, как это делается и в отечественном методе расчета балочных элементов. Второй коэффициент τa вычисляется из деформационной теории путем обработки кривой коэффициента продольного изгиба в методе предельного состояния.
Поэтому можно предположить, что и упруго-пластический момент балки может быть также вычислен с помощью коэффициента редукции τb:
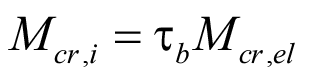 . (79)
. (79)
Коэффициент редукции балки τb в деформационной теории можно переписать через коэффициент устойчивости φb и условную изгибно-крутильную гибкость 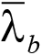 :
:
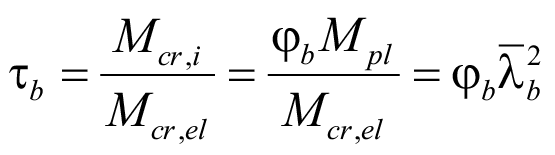 . (80)
. (80)
В упругой области гипербола Эйлера с учетом влияния градиента момента Cb:
 . (81)
. (81)
Из (80) выразим условную гибкость и подставим в (81). Получим упруго-пластическое равенство:
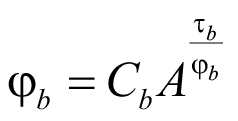 . (82)
. (82)
Используя свойство логарифма ax = ex×lna = lna×ex и свойство экспоненты ex = b → lnb = x, найдем τb:
 . (83)
. (83)
Степень n = 1,5 соответствует числовому коэффициенту в показательной функции (78) A ≈ 0,63. А кривая продольного изгиба b центрально-сжатой колонны со случайными эксцентриситетами по отечественным нормам [4] и кривая 2P по нормах США коэффициентам равны A = 0,615 и A = 0,658 соответственно. Что делает формулу (78) в методе прямого расчета стальных конструкций универсальной для описания устойчивости центрально-сжатой колонны со случайными эксцентриситетами и балки с начальными несовершенствами в деформационной теории.
Если для расчета балок принять A = 0,63, тогда при чистом изгибе получим уравнение:
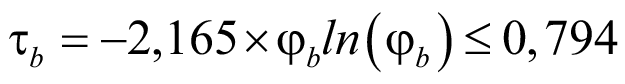 . (84)
. (84)
Для расчета двутавровых центрально-сжатых колонн при A = 0,615 при одинаковых эксцентриситетах по СП 16.13330.2017 [4]:
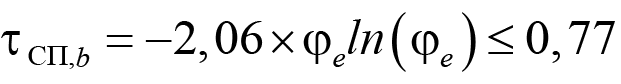 , (85)
, (85)
где φe – нормативные значения коэффициента продольного изгиба для кривой b.
Коэффициент редукции τa согласно нормам [15]:
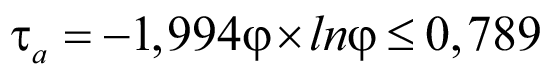 . (86)
. (86)
В нормативном методе расчета по бифуркационной теории вводят эмпирический понижающий коэффициент γc = 0,87, который учитывает совокупность геометрических несовершенств. Поэтому упругий критический изгибающий момент, определяемый по формуле (68), умножается на γc в обязательном порядке. Из деформационной теории следует, что γc = 0,8.
Заключение
Вышеизложенный материал был создан с целью демонстрации развития инженерной методики расчета устойчивости плоской формы изгиба двутавровой балки, которая объективно остается одним из самых слабых мест в настоящем своде правил по стальным конструкциям. Продемонстрированный путь решения задачи устойчивости плоской формы двутавровой балки предлагает отказаться от сложных полиномиальных зависимостей ψ(α) и перейти к развитому и универсальному уравнению изгибно-крутильного параметра. Также в статье приводится достаточно простая возможность совершить переход от бифуркационной к деформационной теории расчета балок, используя концепцию формулы Мерчанта и широкомасштабные исследования ученых из Японии. В дополнение к этому рассмотренный коэффициент редукции в методе прямого расчета строительных конструкций может объединить продольный изгиб балок и колонн в одно единое целое.
Список литературы
1. <i>Власов В.З.</i> Тонкостенные упругие стержни. Москва: Физматгиз; 1959.
2. <i>Броуде Б.М.</i> Предельные состояния стальных балок. Москва: Стройиздат; 1953.
3. <i>Ильин В.П.</i> Численные методы решения задач строительной механики. Минск: Вышэйшая школа; 1990.
4. СП 16.13330.2017. Стальные конструкции. Актуализированная редакция СНиП II-23-81*. Москва: Минстрой России; 2017.
5. СП 294.1325800.2017. Конструкции стальные. Правила проектирования. Москва: Минстрой России; 2017.
6. <i>Градштейн И.С.</i> Таблицы интегралов. Москва: Физмат; 1963.
7. <i>Алексеев П.И.</i> Устойчивость стержней и балок. Киев: Будивельник; 1964.
8. <i>Uzun E.T.</i> Lateral torsional buckling of doubly symmetric I-shaped steel members under linear moment. Pamukkale University Journal of Engineering Sciences. 2019;25(6):635–642. https://doi.org/10.5505/pajes.2018.46656.
9. <i>Fukumoto Y.</i> Lateral-torsional buckling strength of steel beams from test data. Proceedings of the Japan Society of Civil Engineers. 1984;1984(341):137–146. https://doi.org/10.2208/jscej1969.1984.137.
10. <i>Itoh Y.</i> Experimental and numerical analysis database on structural stability. Engineering Structures. 1996;18(10):812–820. https://doi.org/10.1016/0141-0296(96)00010-7.
11. <i>Kubo M.</i> Effects of moment distribution on lateral-torsional buckling strength of rolled steel I-beams. Doboku Gakkai Ronbunshu.1986;1986(368):255–263. https://doi.org/10.2208/jscej.1986.368_255.
12. <i>Kubo M., Fukumoto Y.</i> Lateral-torsional buckling of thin-walled I-beams. Journal of Structural Engineering. 1988;114(4):841–855. https://doi.org/10.1061/(ASCE)0733-9445(1988)114:4(841).
13. <i>Tide R.H.R.</i> Reasonable Column Design Equations. In: Conference Proceedings, Annual Technical Session of Structural Stability Research Council, April 16–17, Cleveland, Ohio, Lehigh University, Bethlehem, PA, 1985. Available at: https://www.aisc.org/globalassets/aisc/manual/15th-ed-ref-list/reasonable-column-design-equations.pdf.
14. <i>Bjorhovde R., Tall L.</i> Development of Multiple Column Curves. IABSE reports of the working commissions. 1975;23:378–384.
15. ANSI/AISC 360-22. Specification for Structural Steel Buildings [internet]. American Institute of Steel Construction; 2022. Available at: https://www.aisc.org/globalassets/product-files-not-searched/publications/standards/a360-22w.pdf.
Об авторе
А. О. ИльюшенковРоссия
Александр Олегович Ильюшенков, инженер промышленного и гражданского строительства, АО «Территориальный проектный институт «Хабаровскпромпроект», Хабаровск
ул. Уссурийский бульвар, д. 2, г. Хабаровск, 680000, Российская Федерация
e-mail: revivaltree@gmail.com
Рецензия
Для цитирования:
Ильюшенков А.О. Развитие инженерной методики расчета устойчивости плоской формы изгиба двутавровой балки. Вестник НИЦ «Строительство». 2025;46(3):22-42. https://doi.org/10.37538/2224-9494-2025-3(46)-22-42. EDN: FKKCEI
For citation:
Ilyushenkov A.O. Development of engineering methodology for calculating the plane bending stability of an I-beam. Bulletin of Science and Research Center of Construction. 2025;46(3):22-42. (In Russ.) https://doi.org/10.37538/2224-9494-2025-3(46)-22-42. EDN: FKKCEI