Перейти к:
Учет горизонтально-вращательных колебаний фундаментов при вычислении сейсмических сил
https://doi.org/10.37538/2224-9494-2021-4(31)-66-78
Аннотация
В статье приводится и иллюстрируется на примере расчета семиэтажного здания-башни с массивным фундаментом метод и алгоритм расчета плоских колебаний сооружений на сейсмические воздействия с учетом смещения фундамента, близкого к горизонтально-вращательным колебаниям, при вычислении сейсмических сил. Построены передаточные функции для массивного жесткого тела, которые используются при расчете фундаментов на горизонтальные силы и моменты, передающиеся на внешнюю плоскость фундамента от сейсмических сил. Результаты расчета зданий – гибких с первой частотой ~2,4 Гц и более жестких с первой частотой 7,1 Гц – показали, что значения приведенных сейсмических сил в зависимости от жесткости зданий возрастают в 1,5–2 раза. Полученные качественные и частично количественные результаты означают, что при проектировании сооружений в сейсмоопасных районах в той или иной форме следует учитывать возможную податливость фундаментов при различных типах грунта и конструктивных решений самих сооружений.
Ключевые слова
Для цитирования:
Чернов Ю.Т., Кбейли Д. Учет горизонтально-вращательных колебаний фундаментов при вычислении сейсмических сил. Вестник НИЦ «Строительство». 2021;31(4):66-78. https://doi.org/10.37538/2224-9494-2021-4(31)-66-78
For citation:
Chernov Yu.T., Qbaily J. Accounting for horizontal torsional vibrations of foundations when calculating seismic load. Bulletin of Science and Research Center of Construction. 2021;31(4):66-78. (In Russ.) https://doi.org/10.37538/2224-9494-2021-4(31)-66-78
-
Основные зависимости
Метод и алгоритм расчета иллюстрируются на примере семиэтажного здания-башни с массивным фундаментом в виде железобетонного блока, на который передаются усилия от сейсмических сил в виде горизонтальной составляющей и момента (рис. 1). Рассматриваются плоские колебания в направлении меньшей жесткости (рис. 1) [1][2].

Рис. 1. а – общая схема фасада; б – вид с торцевой части
Fig. 1. а – the general plane of the facade; б – end view
Для некоторых типов зданий, конструктивная схема которых позволяет считать, что плоскость x0z, проходящая через центр масс, является плоскостью симметрии реакций грунта под фундаментом, система трех уравнений плоских колебаний распадается на уравнение вертикальных и систему горизонтально-вращательных колебаний. Вычисленные по известной схеме передаточные (ПФ) и импульсные (ИПФ) переходные функции и определяют принятый алгоритм расчета [3]:
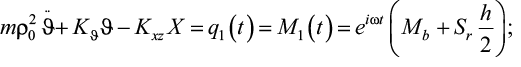
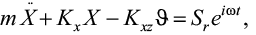 (1)
(1)
где 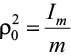 – приведенный радиус инерции;
– приведенный радиус инерции;
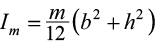 – момент инерции массы фундамента относительно оси 0y;
– момент инерции массы фундамента относительно оси 0y;
m – масса фундамента;
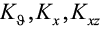 – коэффициенты, определяющие упругие свойства грунта в зависимости от величины
– коэффициенты, определяющие упругие свойства грунта в зависимости от величины  и вида напряженного состояния:
и вида напряженного состояния:
– в основании: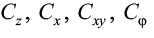 – соответственно равномерного сжатия, равномерного сдвига, неравномерного сдвига, неравномерного сжатия;
– соответственно равномерного сжатия, равномерного сдвига, неравномерного сдвига, неравномерного сжатия;
– по боковым граням: 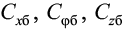 – равномерного бокового сжатия, неравномерного сжатия, равномерного сдвига;
– равномерного бокового сжатия, неравномерного сжатия, равномерного сдвига;
– по торцевым граням: 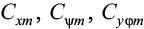 – равномерного сдвига, неравномерного сдвига, при повороте относительно оси 0y.
– равномерного сдвига, неравномерного сдвига, при повороте относительно оси 0y.
Равнодействующие усилий от реакций грунта показаны на рис. 2. Формулы для вычисления реакций и моментов от них приведены ниже. Значения моментов во всех случаях зависят от величины и направлений равнодействующих.

Рис. 2. Положительные направления реакций в системе:
а – при горизонтальном смещении фундамента вправо;
б – при повороте фундамента по часовой стрелке
Fig. 2. Positive directions of response in the system:
а – the foundation is horizontally shifted to the right;
б – the foundation is rotated clockwise
При единичном смещении центра масс:
– горизонтальные реакции в основании и моменты от этих реакций:
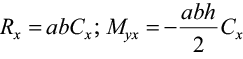 ; (2)
; (2)
– равнодействующая горизонтальных реакций по боковым граням и моменты:
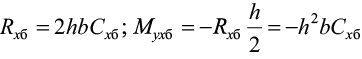 ; (3)
; (3)
– равнодействующие реакции на торцах и моменты относительно оси y:
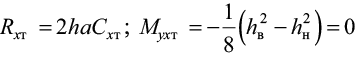 . (4)
. (4)
При единичном повороте относительно оси Оy:
– вертикальные реакции в основании и моменты:
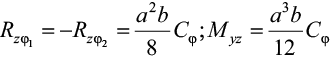 ; (5)
; (5)
– равнодействующие горизонтальных реакций в основании и моменты:
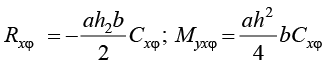 ; (6)
; (6)
– равнодействующие горизонтальных реакций по боковым граням и моменты:
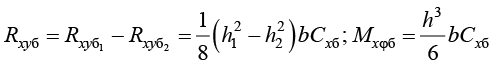 ; (7)
; (7)
– суммарная вертикальная реакция по боковым граням и момент:
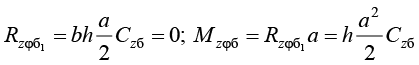 . (8)
. (8)
Воспользовавшись зависимостями (2)–(8), запишем формулы для вычисления коэффициентов системы (1):
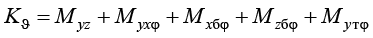 ;
;
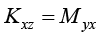 ;
;
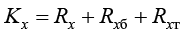 . (9)
. (9)

Следуя общей схеме записи ПФ и ИПФ, полагаем в определителе системы (1) ω2 = p2, и приравняв его нулю, получают частотное уравнение, корни которого определяют частоты собственных колебаний системы. В частности, при 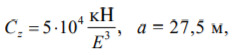
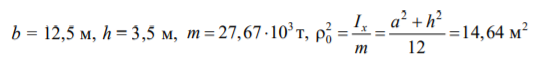 частоты собственных колебаний вычислим из уравнения [4]:
частоты собственных колебаний вычислим из уравнения [4]:
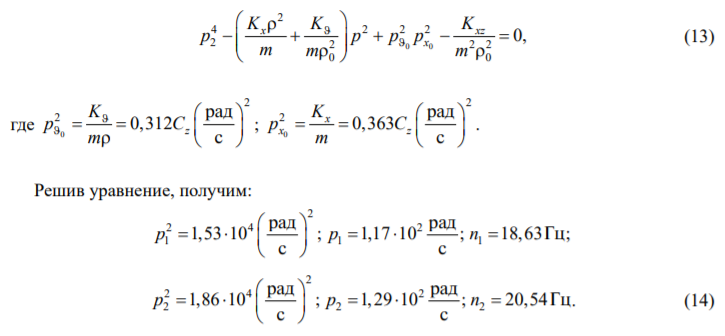
-
Передаточные иимпульсные переходные функции взадачах расчета плоских колебаний массивных тел в грунте
При построении передаточных функций уравнение (1) принимает вид [5]:
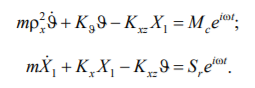 (15)
(15)
Подставив в (15) , после сокращения на получим уравнение форм для этого случая:
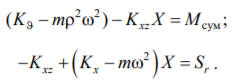 (16)
(16)
Определитель системы вычислен в (13), (14).
Формулы для передаточных функций записываются так [6]:
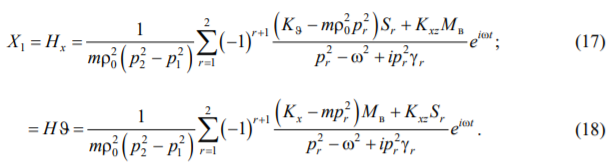
Коэффициенты при можно вычислить, выделив действительную часть в зависимостях (17), (18). Например:
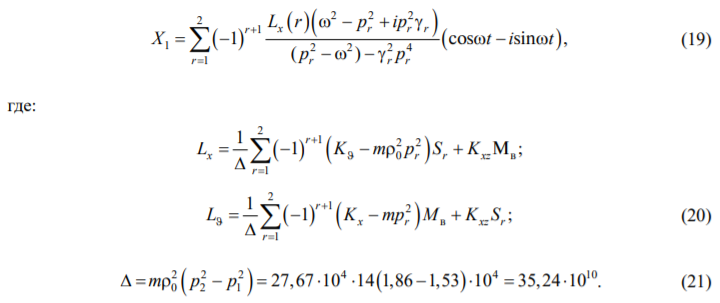
Приняв 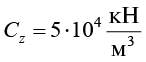 для грунтов, уточним значение коэффициентов в уравнении (1). Тогда:
для грунтов, уточним значение коэффициентов в уравнении (1). Тогда:
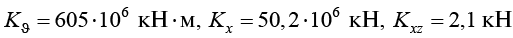 . (22)
. (22)
Значения Lx и Lϑ вычислим по формулам (20). Получаем:
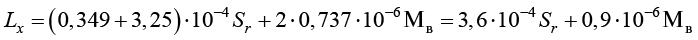 ; (23)
; (23)
 . (24)
. (24)
В результате можем записать:
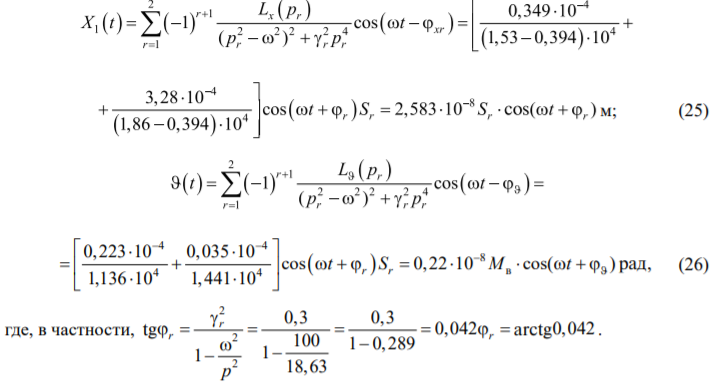
Влияние колебаний фундамента на величины сейсмических сил можно оценить, сравнивая амплитудные значения ускорений грунта с дополнительными амплитудами ускорений и сейсмических сил, определенных с учетом горизонтально-вращательных колебаний фундамента. Где, в частности, используя модифицированную гипотезу Фойгта и полагая 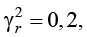 запишем [7][8]:
запишем [7][8]:
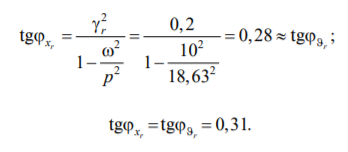
-
Пример расчета
Влияние перемещений фундамента от вычисленных ранее сейсмических сил оценим на примере расчета семиэтажного здания-башни (рис. 3).
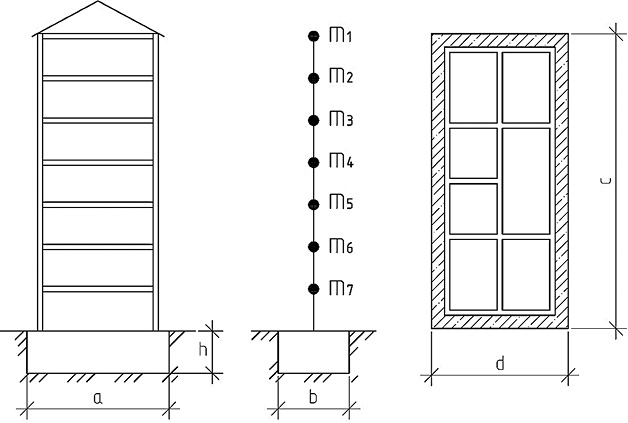
Рис. 3. Вертикальный и горизонтальный разрезы (а, в); расчетная схема (б)
Fig. 3. Vertical and horizontal sections (а, в); calculation scheme (б)
Размеры и масса фундамента: 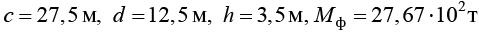 .
.
При вычислении сейсмических сил ограничимся первой формой, нормированные значения ординат которой:
(0,0176; 0,0147; 0,0116; 0,0085; 0,0055; 0,003; 0,001). (27)
Приведенные массы:
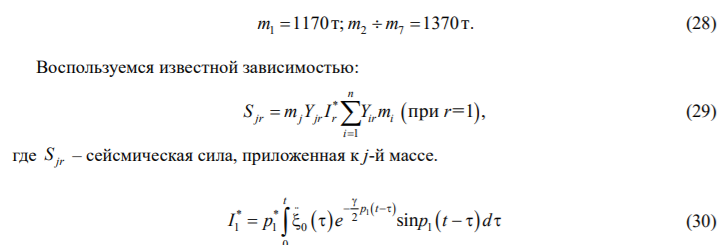
Поскольку речь идет об оценке влияния колебаний фундамента на сейсмические силы, примем некоторую идеализированную зависимость для 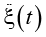 :
:

На верхнюю плоскость фундамента при амплитудных значениях сейсмических сил передаются:

Используя зависимости (31)–(38), вычислим:
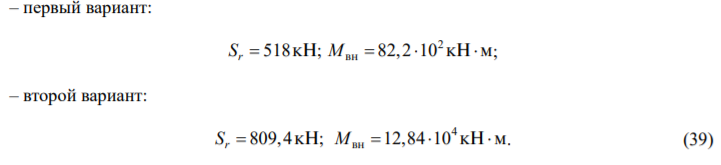
Перемещения центра масс фундамента и угол поворота относительно оси Oy для обоих вариантов определим из зависимостей (23)–(26):
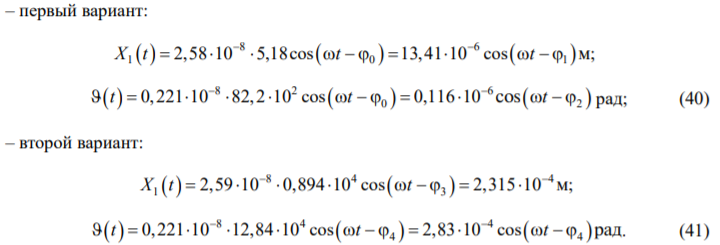
Дополнительные горизонтальные ускорения центра масс при частоте воздействия 10 Гц ( вычислим, воспользовавшись (40), (41). Получаем:

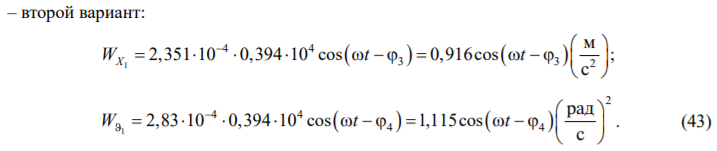
Влияние дополнительных перемещений (и ускорений) центра масс фундамента на величины сейсмических сил оценивалось сравнением величины дополнительных и начальных ускорений. При оценке влияния угла поворота относительно оси Oy следует учитывать дополнительные сейсмические силы, величина которых может быть значительной.
При оценке влияния колебаний фундамента на величину сейсмических сил следует учитывать:
а) сейсмические силы и моменты при горизонтальном смещении центра масс;
б) сейсмические силы и моменты при угле поворота относительно оси Oy.
В примере частота вынужденных колебаний принята равной 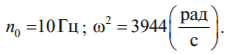 Дополнительные горизонтальные силы и моменты следует вычислять по формулам:
Дополнительные горизонтальные силы и моменты следует вычислять по формулам:
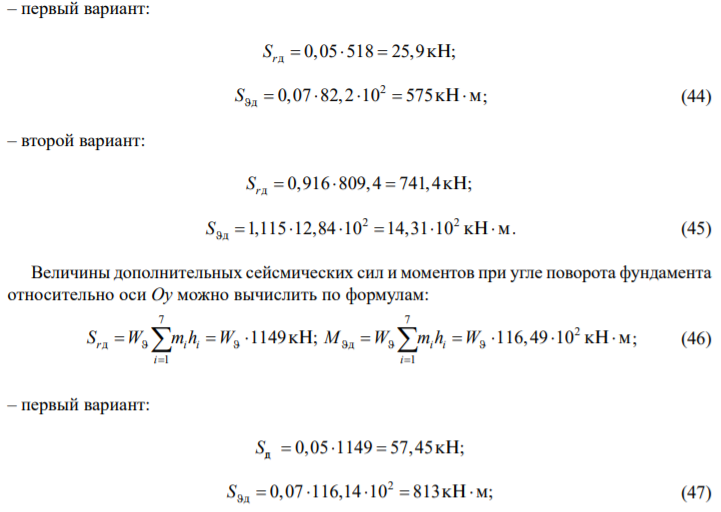
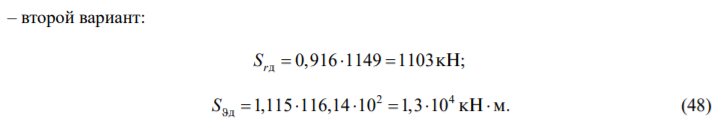
Результаты расчетов сведены в таблице.
Таблица
Сейсмические силы и моменты, возбуждаемые при горизонтально-вращательных колебаниях фундамента, и их сравнение с начальными величинами
Table
Seismic forces and moments excited by horizontal torsional vibrations
of the foundation, and their comparison with the initial values
|
Начальные |
При горизонтальном |
При угловых |
Отношение |
||||||
|
сейсмических сил, кН |
моментов, кН·м |
ускорение, м/с2 |
сейсмические силы, кН |
моменты, кН·м |
ускорение (рад/с)2 |
сейсмические силы, кН |
моменты, кН·м |
сейсмические силы |
моменты |
|
Первый вариант |
|||||||||
|
518 |
8220 |
0,05 |
25,9 |
575 |
0,07 |
57,45 |
813 |
16 |
16,8 |
|
Второй вариант |
|||||||||
|
8094 |
128400 |
0,916 |
7414 |
1432 |
1,115 |
9024 |
14310 |
101 |
112 |
-
Выводы
- Жесткость надфундаментного строения заметно влияет на величины сейсмических сил и моментов, связанных с горизонтально-вращательными колебаниями фундамента. При увеличении первой собственной частоты здания с 2,4до 7,1Гц суммарные значения сейсмических сил увеличиваются ~ в 2 раза, что, естественно, увеличивает расчетную балльность.
- Уточнение результатов расчета реальных зданий связано:
- с учетом сдвига фаз между величинами сейсмических сил и перемещениями фундамента;
- уточнением величин суммарных сейсмических сил и характера ихизменений во времени. - Из-заусловностей в задании упругих характеристик грунта количественные результаты, полученные в работе, следует рассматривать как качественные и достаточно приближенные. Хотя полученные соотношения, на наш взгляд, представляют определенный интерес при проектировании сейсмостойких зданий.
Список литературы
1. Савинов О.А. Современные конструкции фундаментов под машины и их расчет / О.А. Савинов. – 2-е изд. – Л.: Стройиздат, 1979. – 346 c.
2. Пятецкий В.М. Современные фундаменты машин и их автоматизированное проектирование / В.М. Пятецкий, Б.К. Александров, О.А. Савинов. – М.: Стройиздат, 1993. – 415 с.
3. Чернов Ю.Т. Вибрации строительных конструкций. Аналитические методы расчета. Основы проектирования и нормирования вибраций строительных конструкций, подвергающихся эксплуатационным динамическим воздействиям / Ю.Т. Чернов. – 2-е изд., испр. и доп. – М.: АСВ, 2011. – 383 с.
4. Чернов Ю.Т., Зебилила М. К расчету систем виброизоляции с демпферами вязкого трения / Ю.Т. Чернов // Сейсмостойкое строительство. Безопасность сооружений. – 2018. – № 2. – С. 34–38.
5. Коренев Б.Г. Динамический расчет зданий и сооружений (Справочник проектировщика) / Б.Г. Коренев, И.М. Рабинович. – 2-е изд., перераб. и доп. – М.: Стройиздат, 1984. – 303 с.
6. Бахвалов Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – 6-е изд. – М.: БИНОМ. Лаборатория знаний, 2008. – 636 с.
7. Пособие по проектированию конструкций зданий, испытывающие динамические воздействия: РТМ 6596‐86 / ЦНИИСК им. В.А. Кучеренко. – Москва, 1986.
8. Руководство по проектированию виброизоляции машин и оборудования / ЦНИИСК им. В.А. Кучеренко. – М.: Стройиздат, 1972. – 157 с.
Об авторах
Ю. Т. ЧерновРоссия
Юрий Тихонович Чернов, д-р техн. наук, профессор кафедры строительной и теоретической механики
Ярославское шоссе, д. 26, г. Москва, 129337
Дж. Кбейли
Россия
Джаафар Кбейли, аспирант кафедры строительной и теоретической механики
Ярославское шоссе, д. 26, г. Москва, 129337
Рецензия
Для цитирования:
Чернов Ю.Т., Кбейли Д. Учет горизонтально-вращательных колебаний фундаментов при вычислении сейсмических сил. Вестник НИЦ «Строительство». 2021;31(4):66-78. https://doi.org/10.37538/2224-9494-2021-4(31)-66-78
For citation:
Chernov Yu.T., Qbaily J. Accounting for horizontal torsional vibrations of foundations when calculating seismic load. Bulletin of Science and Research Center of Construction. 2021;31(4):66-78. (In Russ.) https://doi.org/10.37538/2224-9494-2021-4(31)-66-78


























