Перейти к:
Динамический анализ сооружений АЭС совместно с грунтовым основанием на сейсмическое воздействие
https://doi.org/10.37538/2224-9494-2021-4(31)-79-88
Аннотация
При проведении расчетов сооружений совместно с грунтовым основанием с использованием специализированных программных комплексов на действие сейсмического нагружения прямыми динамическими методами используются различные подходы моделирования сейсмовоздействия и совместной работы сооружения и грунтового основания. В данной работе проведены расчеты кинематических параметров сооружения совместно с грунтовым основанием для различных моделей сооружения и грунтового основания с использованием специализированных ПК SCAD и STAR_T. Проведены расчеты эталонного сооружения типа этажерка на сейсмические воздействия интенсивностью 7 баллов. В результате проведенных расчетов получены расчетные поэтажные акселерограммы и построены поэтажные спектры ответа. Проведен анализ и сравнение результатов расчета по различным методикам и моделям сооружения.
Ключевые слова
Для цитирования:
Коваль C.В., Кузьминов А.В., Родин П.А., Сидоров Н.М. Динамический анализ сооружений АЭС совместно с грунтовым основанием на сейсмическое воздействие. Вестник НИЦ «Строительство». 2021;31(4):79-88. https://doi.org/10.37538/2224-9494-2021-4(31)-79-88
For citation:
Koval S.V., Kuzminov A.V., Rodin P.A., Sidorov N.M. Dynamic seismic analysis of nuclear power plant buildings and bearing stratum. Bulletin of Science and Research Center of Construction. 2021;31(4):79-88. (In Russ.) https://doi.org/10.37538/2224-9494-2021-4(31)-79-88
При проведении расчетов сооружений совместно с грунтовым основанием с использованием специализированных программных комплексов на действие сейсмического нагружения прямыми динамическими методами используются различные подходы моделирования сейсмовоздействия и совместной работы сооружения и грунтового основания.
В качестве расчетных моделей могут использоваться различные конечные элементы, моделирующие строительные конструкции.
Немаловажную роль играет и выбор метода расчета динамических процессов на продолжительном отрезке времени, свойственном сейсмическим процессам, продолжительностью десятки секунд.
Основания, фундаменты, перекрытия, покрытия, стены, ригели, балки и другие конструкции сооружений могут моделироваться различными конечными элементами и их комбинациями, включающими стержневые, оболочечные, пластинчатые, объемные конечные элементы.
В данной работе проведены расчеты и проанализированы результаты расчета кинематических параметров сооружения совместно с грунтовым основанием для различных моделей сооружения и грунтового основания.
Оценка параметров сейсмических колебаний модельного сооружения совместно с грунтовым основанием проведена с использованием специализированных ПК SCAD и STAR_T /3/.
В качестве задачи выбрана железобетонная «этажерка» на плитном фундаменте совместно с грунтовым массивом. Рассматривается сооружение, представляющее собой трехэтажную конструкцию, состоящую из абсолютно жесткой фундаментной плиты толщиной 500 мм, на которую опираются шесть колонн сечением 500 × 800 мм, и трех перекрытий толщиной 300 мм на отметках 3, 6 и 9 м, шаг колонн 3 × 5 м. Центр координат находится в геометрическом центре фундаментной плиты.
Исходные данные для расчета:
- h =0,3 м – толщина плит перекрытия;
- Н= 0,5 м – толщина фундаментной плиты;
- сечение колонн 500 × 800 мм;
- ρ1 = 2,5т/м3 – плотность материала конструктивных элементов;
- Е= 3,1 × 1010 Па – модуль упругости конструктивных элементов;
- μ1= 0,17 – коэффициент Пуассона конструктивных элементов;
- ξ = 0,07– коэффициент затухания конструктивных элементов;
- ρ2 = 2,0т/м3 – плотность материала грунта;
- μ2= 0,25 – коэффициент Пуассона грунта;
- v= 350 м/с – скорость поперечной волны в грунте.
Для анализа кинематических параметров выбраны:
- вПК SCAD (точка покрытия);
- вПК STAR_T (свободная поверхность грунта, фундаментная плита, точка покрытия).
Расчет в SCAD
Рассматривается этажерка из пластинчатых и стержневых элементов (рис. 1а), модель основания – пружина конечной жесткости, к которой приложены акселерограммы. Вязкие свойства грунта учитываются демпфированием по Релею.

Рис. 1. а – конечно-элементная модель из стержневых и пластинчатых элементов; б – общий вид расчетной области
Fig. 1. a – finite element model of bar and plate elements; б – general view of computational domain
Воздействие на сооружение задается трехкомпонентной синтезированной акселерограммой уровня проектного землетрясения (ПЗ) интенсивностью 7 баллов по шкале MSK-64. Максимальные ускорения в горизонтальных направлениях составляют 0,12 g, в вертикальном – 0,08 g. Длительность воздействия равняется 22,5 с (в рассматриваемом примере длительность воздействия ограничена 10 с), шаг оцифровки – 0,01 с (рис. 2а).
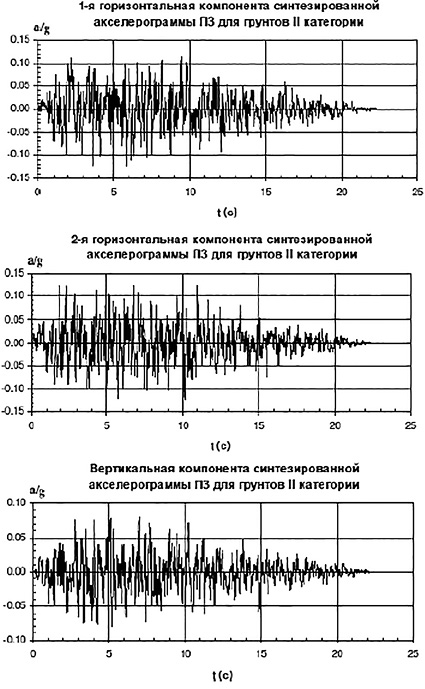
Рис. 2. а – трехкомпонентная акселерограмма; б – расчетная акселерограмма на покрытии – SCAD (Amax = 0,5 м/c2)
Fig. 2. a – three-component accelerogram; б – calculated accelerogram on surface – SCAD (Amax = 0.5 m/s2)
Расчет в STAR_T
Рассматривается волновая контактная задача об распространении волны в полупространстве. Расчетная область состоит из сооружения и полупространства и моделируется объемными изопараметрическими 8-точечными конечными элементами типа трапецоид (рис. 3).
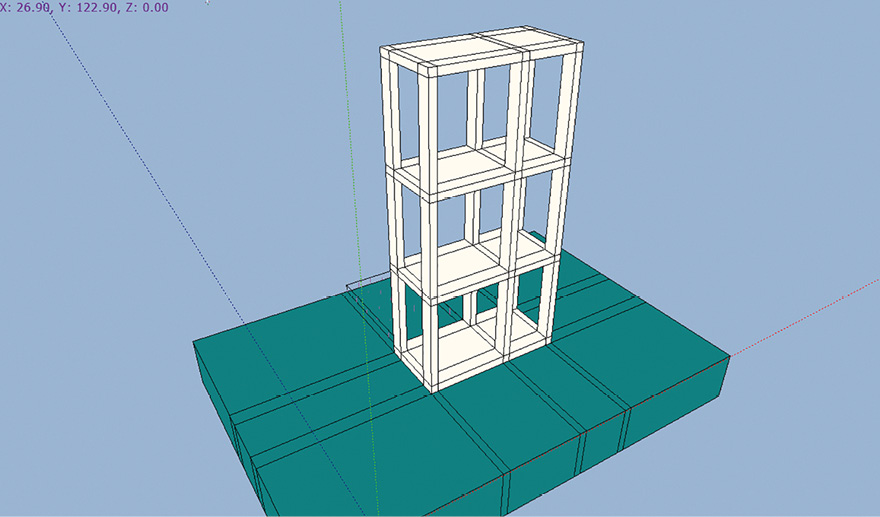
Рис. 3. Общий вид расчетной области модельной задачи (белый цвет – железобетон, зеленый цвет – грунтовое основание)
Fig. 3. General view of computational domain for model problem (white – reinforced concrete, green – soil base)
Исходные данные
Вязкопластические свойства грунта учитываются моделью упруго-вязкопластического грунта типа Рыкова – Григоряна.
Основные размеры и физико-механические характеристики расчетной области приведены выше, грунтовый массив под всей областью толщиной 5 м.
Граничные условия – ограничение перемещений только нижней грани расчетной области, боковые грани свободны и не закреплены (усиление условий консервативности).
В качестве начальных условий заданы исходные волновые сейсмические воздействия в грунтовом массиве 1, 2 (выделены на расчетной схеме объемы грунта, рис. 4) в виде трехкомпонентных ускорений.
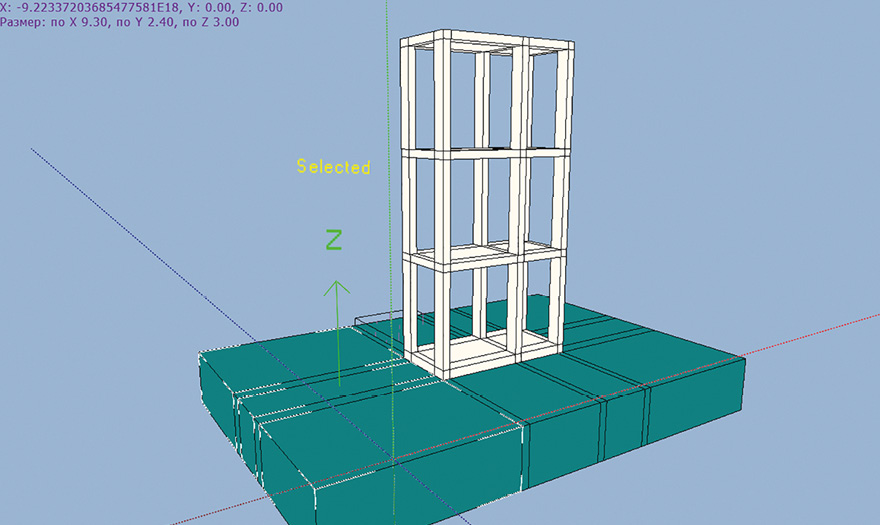
Рис. 4. Выделенные объемы с заданными начальными ускорениями А1, А2, А3 = 1 м/с2
Fig. 4. Selected volumes with given initial accelerations A1, A2, A3 = 1 m/s2
На свободной поверхности фундаментной плиты, грунтового основания и наземного строения задаются точки, в которых необходимо получить графики акселерограмм для сравнения их значений на грунте и фундаментной плите, а также для построения поэтажных спектров ответа на конструкциях верхнего строения (стены, колонны, ригели, перекрытия, покрытия).
По результатам расчета в STAR_T получены трехкомпонентные акселерограммы

Рис. 5. Точки вывода акселерограмм
Fig. 5. Accelerogram output points
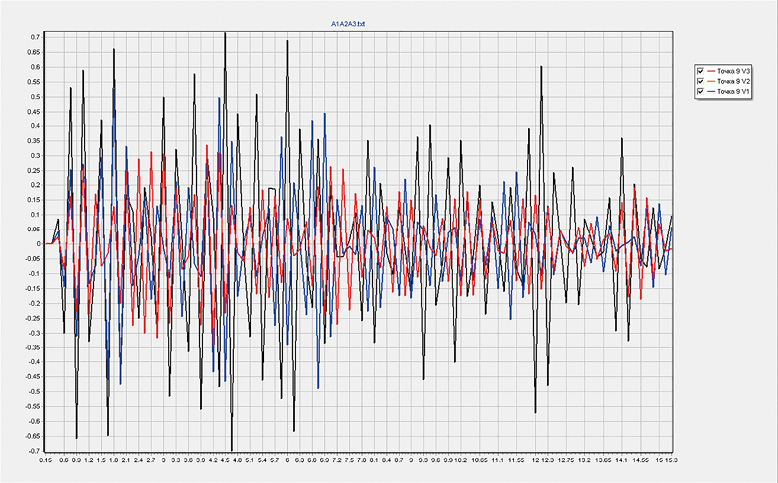
Рис. 6. Расчетные трехкомпонентные акселерограммы на поверхности грунта (3 графика на одном скане Amax = 0,7 м/c2)
Fig. 6. Calculated three-component accelerograms on ground surface (3 graphs in one scan Amax = 0.7 m/s2)
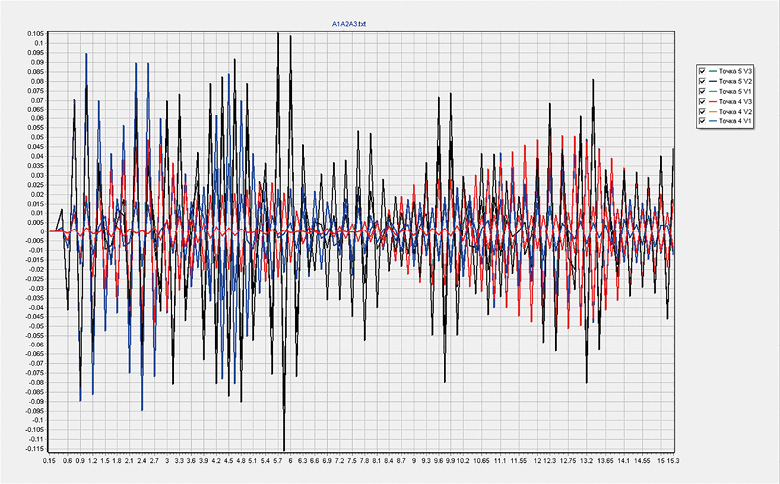
Рис. 7. Расчетные трехкомпонентные акселерограммы на фундаментной плите, Amax = 0,1 м/c2
Fig. 7. Calculated three-component accelerograms on raft foundation, Amax = 0.1 m/s2
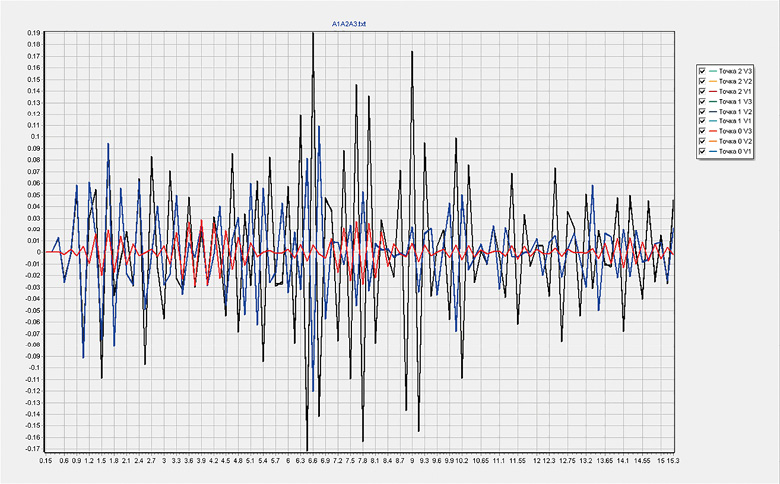
Рис. 8. Расчетные трехкомпонентные акселерограммы на покрытии STAR_T, Amax = 0,19 м/c2
Fig. 8. Calculated three-component accelerograms on surface STAR_T, Amax = 0.19 m/s2
Сравнение спектров ответа по расчетным акселерограммам в ПК SCAD и STAR_T
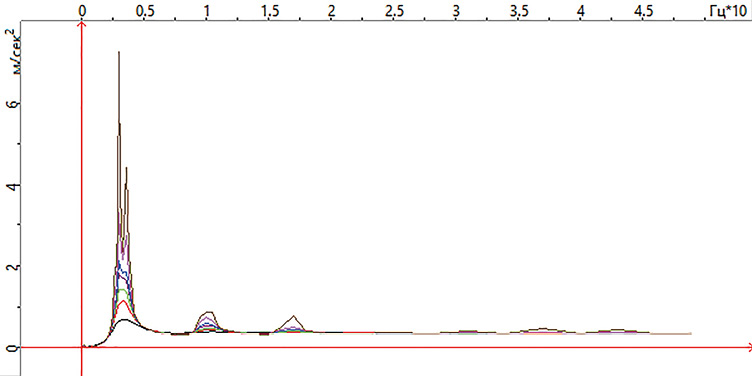
Рис. 9. Спектры ускорений на плите покрытия для всего диапазона логарифмических декрементов (ПК_STAR_T).
Максимальное ускорение – 0,3470324 м/с2 достигается в момент времени 4,05 с
Максимальная скорость – 0,005 м/с2 достигается в момент времени 3,45 с
Максимальное перемещение – 0,003 м достигается в момент времени 10,2 с
Fig. 9. Acceleration spectra on roof slab in entire range of logarithmic decrements (PC_STAR_T).
The maximum acceleration of 0.3470324 m/s2 is achieved at 4.05 s
The maximum speed of 0.005 m/s2 is achieved at 3.45 s
The maximum displacement of 0.003 m is achieved at 10.2 s
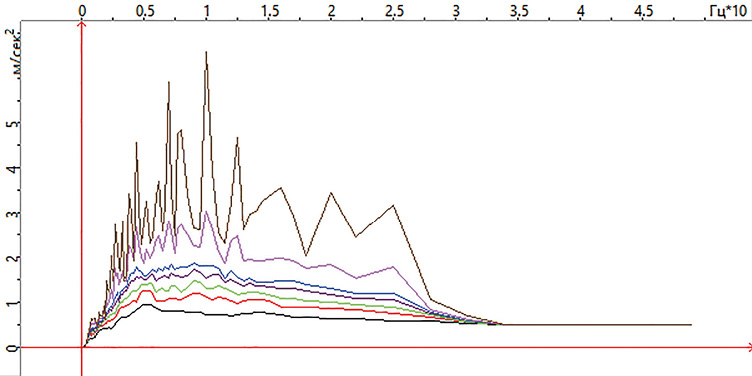
Рис. 10. Спектры ускорений на плите покрытия для всего диапазона логарифмических декрементов (ПК_SCAD).
Максимальное ускорение – 0,50401 м/с2 достигается в момент времени 4,03 с
Максимальная скорость – 0,034 м/с2 достигается в момент времени 4,83 с
Максимальное перемещение – 0,007 м достигается в момент времени 5,11 с
Fig. 10. Acceleration spectra on roof slab in entire range of logarithmic decrements (PC_SCAD).
The maximum acceleration of 0.50401 m/s2 is achieved at 4.03 s
The maximum speed of 0.034 m/s2 is achieved at 3.45 s
The maximum displacement of 0.007 m is achieved at 5.11 s
Результаты расчета кинематических параметров
По схеме точечного приложения акселерограмм в ПК_SCAD ускорения на покрытии достигают максимума 0,5 м/c2, а в ПК STAR_T – 0,2 м/с2.
Выводы
В данной работе проведен прямой динамический расчет для двух различных моделей объекта с использованием ПК SCAD и STAR_T на заданное сейсмовоздействие интенсивностью 7 баллов.
При расчете по упрощенной схеме в ПК SCAD отсутствует возможность получения акселерограмм на грунте и фундаментной плите, т. к. они задаются как исходное воздействие, также при расчетах по упрощенной схеме необходимо проведение многовариантных расчетов с различными коэффициентами демпфирования, т. к. небольшой разброс коэффициентов по Рэлею дает отличающиеся на порядок значения акселерограмм.
Расчет по схеме «сооружение – основание» показал, что при приходе сейсмовоздействия как волнового процесса и моделирования контактной задачи параметры колебаний свободной поверхности и фундаментной плиты отличаются почти на порядок (0,7 м/с2 на грунте и 0,08 м/с2 на фундаментной плите), причем на покрытии они отличаются всего в 2 раза.
При расчете по модели сооружения совместно с грунтовым основанием эти проблемы отсутствуют в связи с возможностью задания любой математической модели деформирования материалов конструкций и грунтового основания как по деформационной теории, так и по теории пластического течения.
Проведенный анализ показал, что для проведения расчетов на сейсмические воздействия наиболее эффективными из методов прямого интегрирования являются неявные методы (в частности примененный в расчетах метод Ньюмарка), обладающие безусловной устойчивостью и не требующие жестких ограничений на шаг по времени и сеточное разбиение расчетной области.
Список литературы
1. Снитко Н.К. Статическое и динамическое давление грунтов и расчет подпорных стенок / Н.К. Снитко. – Ленинград: Госстройиздат, 1963. – 295 с.
2. Глушков Г.И. Расчет сооружений, заглубленных в грунт / Г.И. Глушков. – Москва: Стройиздат, 1977. – 295 с.
3. Коваль С.В. Программный комплекс START_T для проведения расчетов наземных заглубленных и подземных сооружений / С.В. Коваль, Ф.Б. Киселев. – Москва: МГУ, 2014. – Рег. № 2015610074 от 10.11.2014.
Об авторах
C. В. КовальРоссия
Коваль Сергей Всеволодович, д-р техн. наук, заместитель начальника отдела надежности строительных конструкций
ул. Малая Красносельская, д.2/8, к. 5, Москва, 107140
А. В. Кузьминов
Россия
Кузьминов Александр Владимирович, старший научный сотрудник отдела надежности строительных конструкций
ул. Малая Красносельская, д.2/8, к. 5, Москва, 107140
П. А. Родин
Россия
Родин Павел Александрович, младший научный сотрудник отдела надежности строительных конструкций
ул. Малая Красносельская, д.2/8, к. 5, Москва, 107140
тел.: +7 (499) 264-40-45
Н. М. Сидоров
Россия
Сидоров Никита Маркович, младший научный сотрудник отдела надежности строительных конструкций
ул. Малая Красносельская, д.2/8, к. 5, Москва, 107140
Рецензия
Для цитирования:
Коваль C.В., Кузьминов А.В., Родин П.А., Сидоров Н.М. Динамический анализ сооружений АЭС совместно с грунтовым основанием на сейсмическое воздействие. Вестник НИЦ «Строительство». 2021;31(4):79-88. https://doi.org/10.37538/2224-9494-2021-4(31)-79-88
For citation:
Koval S.V., Kuzminov A.V., Rodin P.A., Sidorov N.M. Dynamic seismic analysis of nuclear power plant buildings and bearing stratum. Bulletin of Science and Research Center of Construction. 2021;31(4):79-88. (In Russ.) https://doi.org/10.37538/2224-9494-2021-4(31)-79-88


























