Перейти к:
Сейсмический расчет зданий АЭС с учетом податливости фундаментальной плиты
https://doi.org/10.37538/2224-9494-2021-4(31)-89-97
Аннотация
В настоящей работе предлагается математический метод учета податливости фундаментных плит зданий АЭС при динамических воздействиях. Подобный учет во многих случаях анализа позволяет существенно уточнить результаты, а иногда (для конструкций с «отрезанными» внешними стенами) при падении самолета и воздействии воздушной ударной волны он просто необходим.
Представленный метод базируется на применении «грунтовых» пружин и демпферов из ASCE 4-16, специальным образом распределенных по подошве фундаментной плиты здания.
В заключение представлены результаты расчета интегральных характеристик «грунтовых» пружин и демпферов при реалистичном (седловидном) законе их распределения по подошве фундаментной плиты типового здания.
Ключевые слова
Для цитирования:
Коротков В.А., Югай Т.З. Сейсмический расчет зданий АЭС с учетом податливости фундаментальной плиты. Вестник НИЦ «Строительство». 2021;31(4):89-97. https://doi.org/10.37538/2224-9494-2021-4(31)-89-97
For citation:
Korotkov V.A., Yugai T.Z. Seismic design of NPP structures taking into account foundation slab compliance. Bulletin of Science and Research Center of Construction. 2021;31(4):89-97. (In Russ.) https://doi.org/10.37538/2224-9494-2021-4(31)-89-97
При выполнении сейсмических расчетов в соответствии со стандартом ASCE 4-16 [1] необходимо учитывать эффекты взаимодействия сооружения с грунтовым основанием (SSI) зданий и сооружений АЭС, важных для безопасности. Существуют два основных метода решения данной задачи: прямой метод и метод импедансов. В прямом методе грунт моделируется детально элементами сплошной среды, а в методе импедансов применяются «грунтовые» пружины и демпферы, моделирующие эквивалентную жесткость и затухание. Метод импедансов является эффективным, удобным и часто применяется в расчетах по различным программам: ABAQUS, ANSYS, NASTRAN и др. для проектных целей. Однако эквивалентные характеристики пружин и демпферов определяются для штампа и их использование для реальных зданий АЭС, обладающих податливой фундаментной плитой, возможно только приближенно. Также приближенно учитываются неоднородности в грунте (слоистость, линзы и др.). При выполнении реальных расчетов компенсация названных приближений производится за счет учета вариабельности модуля сдвига в грунте по рекомендациям ASCE 4–16, п. 5.1.7. Для учета податливости фундаментной плиты необходимо выполнить реалистическое распределение эквивалентных жесткостей и затуханий по точкам ее подошвы таким образом, чтобы суммарная по всем точкам распределения жесткость в точности соответствовала эквивалентной жесткости. Суммарное затухание также должно соответствовать эквивалентным затуханиям либо консервативно быть несколько меньше.
В настоящей работе предлагается математический метод решения такой задачи.
Система уравнений движения при сейсмических колебаниях здания имеет вид:
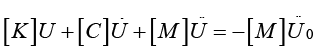 , (1)
, (1)
где
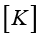 – матрица жесткости;
– матрица жесткости;
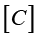 – матрица демпфирования;
– матрица демпфирования;
[M] – матрица массы;
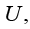
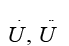 – векторы относительных перемещений, скоростей и ускорений;
– векторы относительных перемещений, скоростей и ускорений;
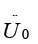 – исходная акселерограмма.
– исходная акселерограмма.
В системе уравнений (1)
[K] = [K1] + [K2], (2)
где [K1] и [K2] – парциальные матрицы жесткости сооружения и грунта соответственно;
[C] = [С1] + [С2], (3)
где [С1] – парциальная матрица демпфирования в материале системы, возникающего за счет трения, [С2] – парциальная матрица излучательного или волнового демпфирования, обусловленная оттоком энергии в грунт при колебаниях здания.
Для определения [K2] и [С2] использовались эквивалентные жесткости и затухания из ASCE 4–16. Обозначим 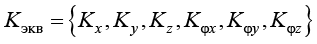 и
и 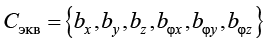 компоненты эквивалентной жесткости и эквивалентного затухания для штампа, показанного на рис. 1. Для формирования матриц [K2] и [C2] величины
компоненты эквивалентной жесткости и эквивалентного затухания для штампа, показанного на рис. 1. Для формирования матриц [K2] и [C2] величины 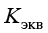 и
и 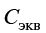 нужно распределить по точкам подошвы фундаментной плиты.
нужно распределить по точкам подошвы фундаментной плиты.
Пусть значения эквивалентных поступательных жесткостей и затуханий при поступательных перемещениях распределяются по произвольному закону z = f(x,y).
Тогда для j-й точки фундаментной плиты выражение для приведенной эквивалентной жесткости можно записать следующим образом:
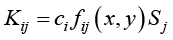 , где i – x, y, z, (4)
, где i – x, y, z, (4)
j – 1, …, N, N – число узловых точек на подошве плиты,
ci – константа,
fij(x,y) – значение функции f(x,y) в точке j по направлению i,
ΔSj – приведенная к точке j площадь фундаментной плиты.
Величину константы ci определим из условия:
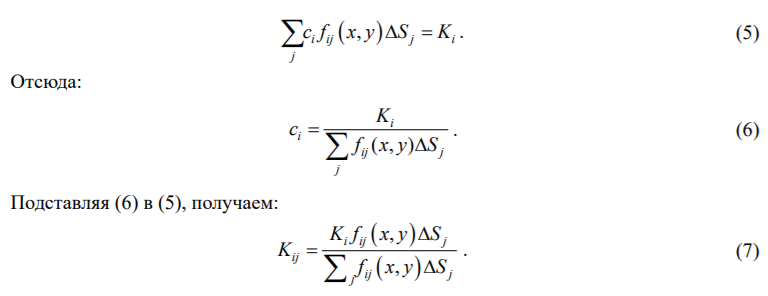
Формула (7) позволяет определить значение поступательной компоненты жесткости в j-й точке фундаментной плиты при произвольном законе распределения по подошве.
Аналогичное выражение для поступательных компонент затухания:
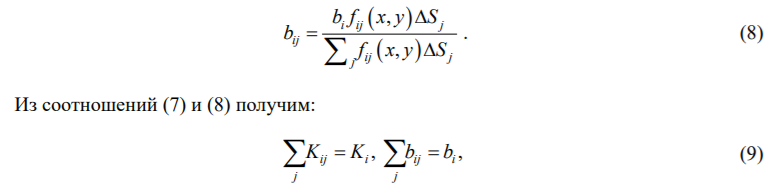
т. е. суммарные (интегральные) поступательные компоненты жесткости и затухания по всем точкам подошвы фундаментной плиты в точности соответствуют эквивалентным значениям.

Таблица 1
Значения коэффициентов при нагружении сосредоточенной силой P0
Table 1
Values of the coefficients under concentrated force loading P0
|
L/B |
a00 |
a20 |
a02 |
a40 |
a22 |
a04 |
a60 |
a42 |
a24 |
a06 |
|
1 |
0.556 |
0.267 |
0.267 |
0.3 |
−0.017 |
0.301 |
0.501 |
0.032 |
0.032 |
0.501 |
|
1.5 |
0.561 |
0.223 |
0.301 |
0.268 |
0.015 |
0.319 |
0.470 |
−0.060 |
0.126 |
0.530 |
|
2 |
0.565 |
0.196 |
0.322 |
0.234 |
0.029 |
0.332 |
0.433 |
−0.054 |
0.129 |
0.550 |
|
3 |
0.581 |
0.161 |
0.339 |
0.185 |
0.061 |
0.345 |
0.353 |
0.020 |
0.130 |
0.567 |
|
5 |
0.597 |
0.134 |
0.355 |
0.139 |
0.078 |
0.356 |
0.247 |
0.074 |
0.118 |
0.593 |
|
7 |
0.607 |
0.120 |
0.363 |
0.115 |
0.074 |
0.363 |
0.196 |
0.090 |
0.113 |
0.606 |
|
10 |
0.616 |
0.108 |
0.369 |
0.094 |
0.069 |
0.370 |
0.155 |
0.102 |
0.105 |
0.616 |
Узловые эквивалентные поступательные жесткости и затухания в совокупности создают интегральную угловую жесткость и затухание за счет вращения:
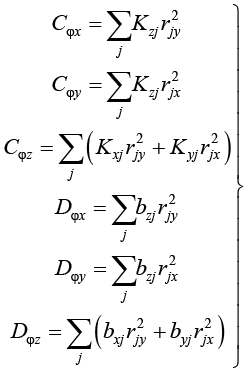 . (12)
. (12)
Здесь rjx и rjy – компоненты радиус-вектора j-й точки, выходящего из геометрического центра фундаментной плиты (рис. 1).
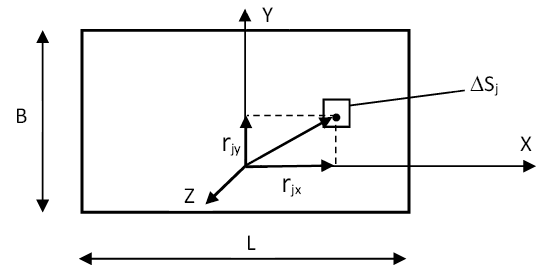
Рис. 1. Прямоугольный штамп
Fig. 1. Rectangular plate
Интегральные угловые жесткости и затухания из (12) существенно отличаются от эквивалентных. Следует отметить, что если расчет эквивалентных и интегральных характеристик грунта проводить по теории Винклера, учитывающей проседание грунта только под штампом, но не в соседних зонах (рис. 2), то отличия не будет.

Рис. 2. Зоны проседания грунта под штампом
Fig. 2. Soil subsidence areas under the plate
Компенсирующая разница в угловых жесткостях и затуханий составит:
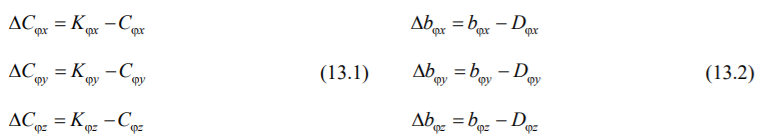
Как показали расчетные исследования на типовых конструкциях значения компенсирующих угловых жесткостей (13.1) положительные, а значения компенсирующих угловых затуханий (13.2) отрицательные. Консервативно принимаем:
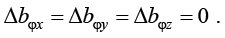 (14)
(14)
Из (14) получаем выражения для скорректированных эквивалентных затуханий:
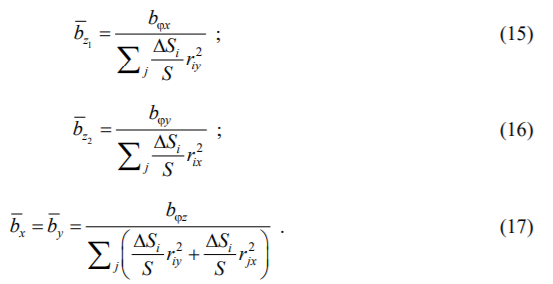
Консервативно принимаются минимальные значения из 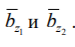 .
.
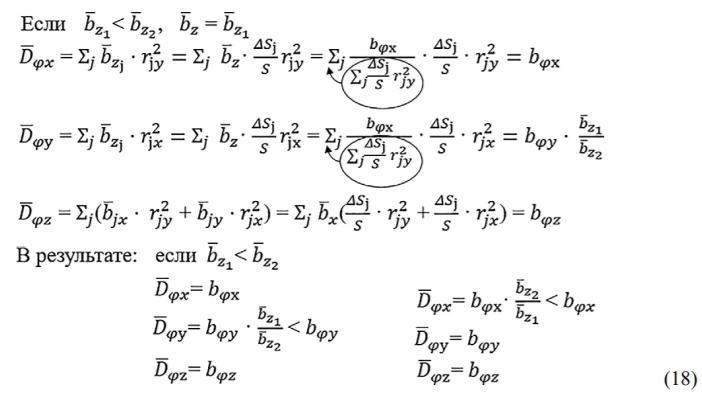
Если L = B, все скорректированные вращательные затухания равны эквивалентным.
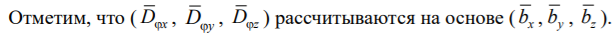
Таким образом, компоненты эквивалентных поступательных жесткостей, полученные по (7), распределяются по подошве фундаментной плиты по «седловидному» закону, а компенсирующие угловые жесткости, полученные по (13.1) – равномерно.
По предложенной методике была составлена программа, совместная с ПС ABAQUS, и выполнен ряд проектных расчетов. Результаты расчетов приводились в докладе на конференции [3].
Скорректированные компоненты эквивалентных поступательных затуханий (15), (16), (17) в совокупности создадут интегральные угловые затухания и, как видно из (18), их величины, в зависимости от соотношения сторон штампа, в точности соответствуют эквивалентным, либо будут несколько ниже.
В табл. 2 представлен пример расчета значений жесткости и затуханий в грунте по данной методике для типового здания. Размеры фундамента здания составляют L = 73 м, B = 50 м,
а общая масса здания – 110 т.
Таблица 2
Пример расчета грунтовых характеристик для типового здания
Table 2
Example of soil characteristics calculated for a typical building
|
Эквивалентные жесткости, кН/м, кН⋅м |
Эквивалентные затухания, кН·с/м, кН⋅с⋅м |
Скорректированные интегральные затухания, кН·с/м, кН⋅с⋅м |
|||
|
Gmin , VS30 = 927 м/с |
|||||
|
Kx, |
3.44E + 08 |
bx |
7.22E + 06 (59 %) |
bx |
4.98E + 06 (41 %) |
|
Ky, |
3.64E + 08 |
by |
7.65E + 06 (60 %) |
by |
4.98E + 06 (40 %) |
|
Kz |
4.13E + 08 |
bz |
1.28E + 07 (95 %) |
bz |
9.53E + 06 (71 %) |
|
Kφx |
2.65E + 11 |
bφx |
2.14E + 09 (25 %) |
bφx |
2.14E + 09 (25 %) |
|
Kφy |
4.55E + 11 |
bφy |
4.90E + 09 (37 %) |
bφy |
4.23E + 09 (32 %) |
|
Kφz |
5.24E + 11 |
bφz |
3.33E + 09 (27 %) |
bφz |
3.33E + 09 (27 %) |
|
Компенсирующие угловые жесткости, кН⋅м |
|||||
|
ΔCφx |
9.845·1010 |
||||
|
ΔCφy |
2.443·1011 |
||||
|
ΔCφz |
1.991·1011 |
||||
Из табл. 2 видно, что компенсирующие угловые жесткости имеют существенные значения и их необходимо учитывать, а компоненты скорректированных интегральных затуханий либо соответствуют эквивалентным значениям затуханий, либо консервативно ниже.
Представленный метод учета податливости фундаментной плиты можно применять в расчетах зданий при особых динамических воздействиях: сейсмика, падение самолета и действие воздушной ударной волны с использованием различных методов анализа.
Также предлагается использовать данный подход в стандарте РФ по сейсмостойкости зданий.
Список литературы
1. ASCE 4–16 Seismic Analysis of Safety-Related Nuclear Structures. – American Society of Civil Engineers (ASCE), 2017. – 202 p.
2. Горбунов-Посадов М.И. Расчет конструкций на упругом основании / М.И. Горбунов-Посадов, Т.А. Маликова, В.И. Соломин. – Москва: Стройиздат, 1984. – 679 с.
3. Коротков В.А. О применимости модального метода динамического анализа в расчётах строительных конструкций АЭС при падении самолета и при сейсмическом воздействии / В.А. Коротков, А.П. Иванов // Инженерные системы–2016: Труды Международного форума (Москва, 4–5 апреля 2016 г.) / Инжиниринговая компания «ТЕСИС». – М.: МАКС Пресс, 2016. – С. 94–105.
Об авторах
В. А. КоротковРоссия
Владимир Анатольевич Коротков, канд. техн. наук, главный специалист БКП-2
ул. Бакунинская, д. 7, к. 1, г. Москва, 107996
Т. З. Югай
Россия
Тамара Захаровна Югай, старший научный сотрудник
Малая Красносельская ул., д. 2/8, к. 5, г. Москва, 107140
Рецензия
Для цитирования:
Коротков В.А., Югай Т.З. Сейсмический расчет зданий АЭС с учетом податливости фундаментальной плиты. Вестник НИЦ «Строительство». 2021;31(4):89-97. https://doi.org/10.37538/2224-9494-2021-4(31)-89-97
For citation:
Korotkov V.A., Yugai T.Z. Seismic design of NPP structures taking into account foundation slab compliance. Bulletin of Science and Research Center of Construction. 2021;31(4):89-97. (In Russ.) https://doi.org/10.37538/2224-9494-2021-4(31)-89-97


























