Перейти к:
Оценка прочности и устойчивости железобетонных конструкций АЭС с учетом результатов вибродиагностики
https://doi.org/10.37538/2224-9494-2022-3(34)-79-91
Аннотация
Введение. Статья носит постановочный характер. В ней представляются методические шаги на пути решения вопроса об оценке ресурса действующих блоков с учетом деградации динамических свойств железобетонных конструкций, полученных методами вибродиагностики на примере «горячих» помещений объектов использования атомной энергии.
Целью статьи является уточнение метода оценки напряженно-деформированного состояния и прочности строительных конструкций АЭС с учетом старения элементов из железобетона при воздействии различных внешних факторов.
Материалы и методы. Предлагается методика оценки прочности (несущей способности) и устойчивости строительных конструкций АЭС, в которых в результате длительной эксплуатации произошли существенные изменения в свойствах железобетона, вызванные нарушением температурного режима их эксплуатации, что привело к ослаблению жесткостей конструктивных элементов и, как следствие, снижению их прочности и устойчивости. В связи с этим для оценки напряженно-деформированного состояния и прочности «горячих» помещений необходимо сделать расчет с учетом истории нагружения конструкций и процесса развития трещин, начиная от времени начала эксплуатации блока до настоящего времени. Однако за время эксплуатации здания не проводился анализ истории температурного нагружения. Также нет подходящей программы для ЭВМ нелинейного динамического анализа, которая учитывает историю нагружения при развитии трещин в железобетонных конструкциях и которая прошла аттестацию в Ростехнадзоре. Компенсация отмеченных недостатков возможна за счет проведения вибродиагностики стен и полов «горячих» помещений и определения следующих динамических характеристик: частот и форм собственных колебаний, логарифмических декрементов затуханий, модулей деформаций и коэффициентов Пуассона для каждого пола и стены.
Далее, после получения экспериментальной информации, необходимо провести расчет напряженнодеформированного состояния и прочности, в котором полученные данные из эксперимента будут использоваться в качестве исходной информации. Методика расчета базируется на неклассическом методе модальной суперпозиции с применением программ для ЭВМ типа ABAQUS, Ansys, Nastran.
Также в статье в качестве проверки методов вибродиагностики представлена оценка динамических характеристик пола на отметке +13,450 в рядах «П»–«Ж».
Результаты. По результатам эксперимента получены значения модуля деформации и частоты собственных колебаний, которые не выходят за пределы диапазона расчетных значений.
Выводы. Представлена методика оценки прочности строительных конструкций действующих АЭС с учетом старения железобетона под воздействием внешних факторов. В работе также проведена оценка достоверности динамических характеристик, полученных методами вибродиагностики.
Ключевые слова
Для цитирования:
Есенов А.В., Коротков В.А., Кузьминов А.В., Родин П.А., Сидоров Н.М., Югай Т.З. Оценка прочности и устойчивости железобетонных конструкций АЭС с учетом результатов вибродиагностики. Вестник НИЦ «Строительство». 2022;34(3):79-91. https://doi.org/10.37538/2224-9494-2022-3(34)-79-91
For citation:
Esenov A.V., Korotkov V.A., Kuzminov A.V., Rodin P.A., Sidorov N.M., Yugai T.Z. Strength and stability assessment of NPP reinforced concrete structures regarding the results of vibration analysis. Bulletin of Science and Research Center of Construction. 2022;34(3):79-91. (In Russ.) https://doi.org/10.37538/2224-9494-2022-3(34)-79-91
Введение
На этапах проектирования новых блоков вопросы расчета НДС и прочности строительных конструкций АЭС определяются в соответствии с российскими нормами [1]. Исходные данные для элементов железобетона при проведении таких расчетов соответствуют предусмотренным в проекте классам бетона.
Для выполнения подобных расчетов российские и зарубежные нормы рекомендуют применять различные методы динамического анализа [2], однако из теоретических соображений наиболее достоверным является неклассический метод модальной суперпозиции [3], позволяющий учитывать грунтовый массив в виде пружин и демпферов. Кроме того, метод реалистично учитывает демпфирование в различных материалах конструкции и гистерезисное демпфирование в грунте за счет применения опции: модальное композитное демпфирование.
Для применения данного метода в расчетах эксплуатируемых энергоблоков АЭС необходимо учитывать факторы старения. Прочность и устойчивость строительных конструкций зданий и сооружений АЭС напрямую зависит от их технического состояния. При появлении дефектов может произойти снижение несущей способности конструкций. Так, в результате действия повышенных температур (до +285 °С вместо +90 °С при нормальной эксплуатации) в строительных конструкциях «горячих» помещений блока АЭС стали возникать не предусмотренные проектом трещины (далее – запроектный случай), что привело к существенному ослаблению жесткостей конструктивных элементов (стен и полов) и, как следствие, снижению их прочности за почти 40-летний период эксплуатации блока.
Применение неразрушающих методов контроля конструкций, позволяющих определить фактические деформационные характеристики конструкций в местах появления дефектов, позволяет отразить в расчете реальное напряженно-деформированное состояние конструкции и установить их фактическую несущую способность. Одними из таких методов являются неразрушающие методы вибродиагностики, основанные на взаимосвязи деформационных характеристик с динамическими характеристиками строительных конструкций. Неклассический метод модальной суперпозиции позволяет достоверно учитывать полученные в результате вибродиагностики динамические характеристики «горячих» помещений (частоты и формы собственных колебаний, модули деформации, логарифмические декременты затуханий, коэффициенты Пуассона) для оценки НДС и прочности.
Таким образом, в данной статье предлагается подход оценки НДС и прочности строительных конструкций АЭС с учетом старения элементов из железобетона при воздействии различных внешних факторов. Подход основывается на следующих этапах:
- геометрически подобном конечно-элементном моделировании систем сооружение – основание;
- получении динамических характеристик фрагментов зданий методами вибродиагностики для дальнейшего использования в расчетах;
- применение неклассического метода модальной суперпозиции для оценки НДС и прочности здания.
Применение вибродиагностики
Одним из перспективных подходов для оценки динамических характеристик зданий, имеющих длительный срок эксплуатации, является вибродиагностика. В ее основе лежит исследование динамических процессов фрагментов здания (пол, стена), вызванных ударными нагрузками. В рамках вибродиагностики определяются динамические характеристики следующим образом:
- по показаниям вибродатчиков, расположенных на исследуемом фрагменте, определяется зависимость ускорения от времени;
- с помощью преобразования Фурье полученный сигнал преобразуется из временной области в частотную;
- далее выделяются пики на резонансных частотах для получения частот собственных колебаний;
- с помощью обратного преобразования Фурье производится получение импульсной реализации по выделенному тону во временной области для расчета логарифмического декремента затуханий;
- за счет выделения крутильного тона колебаний возможно определение модуля сдвига и коэффициента Пуассона.
На рис. 1 показан пример выделения первого тона собственных колебаний пола на отметке +13,450. Как видно из рис. 1, частота собственных колебаний составляет 37,5 Гц.

Рис. 1. Выделение 1 тона свободных колебаний для пола на отметке +13,450
Fig. 1. Determining 1 mode of natural vibrations for floor at the point +13.450
Оценка динамических характеристик пола
Рассмотрим состояние пола на отметке +13,450, так как данный фрагмент «горячих» помещений наиболее сильно подвергся температурному воздействию. При оценке динамических характеристик пол моделировался прямоугольной композитной плитой размерами a1 = 11,45 м и a2 = 6 м и толщиной h = 0,7 м. На рис. 2 представлено сечение плиты, состоящей из монолитного бетона, имеющего проектный модуль деформации E1 = 2,8 × 107 кН/м2 и из несъемной опалубки, имеющей проектный модуль деформации E2 = 3,25 × 107 кН/м2. Значение коэффициента Пуассона составило ν = 0,2, массовая плотность ρ = 2,4 т/м3. Размеры сечения плиты: h1 = 0,62 м, h2 = 0,08 м. Площади составных частей сечения F1 = 0,62 × 11,45 = 7,1 и F2 = 0,08 × 11,45 = 0,916.P1 = E1 × F1 = 1,988 × 108 и P2 = E2×F2 = 0,297 × 108. l1 = 0,31 – 0,26 = 0,05 и l2 = 0,26 + 0,04 = 0,3.
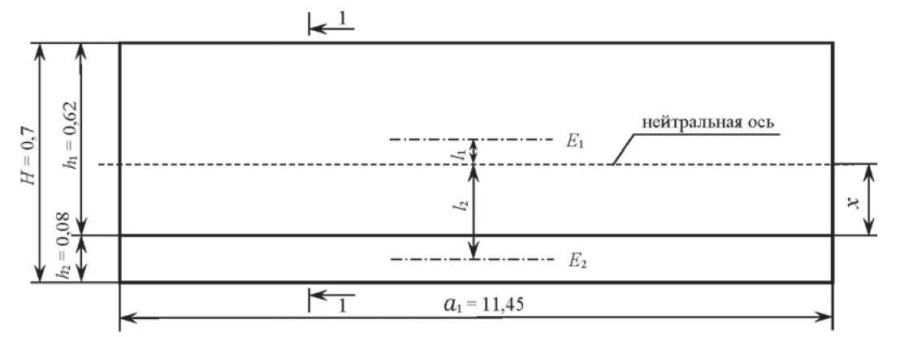
Рис. 2. Сечение фундаментной плиты пола
Fig. 2. Cross-section of floor foundation slab
Определим осредненное значение модуля деформации плиты относительно нейтральной оси из условия:
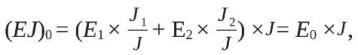
откуда
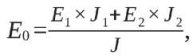
где J, J1, J2 – моменты инерции сечения и его частей относительно нейтральных осей.
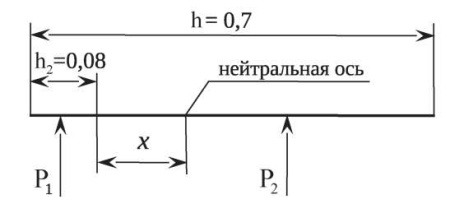
Рис. 3. Поперечный разрез 1-1
Fig. 3. Cross-sectional view 1-1
Для определения осредненного значения модуля деформации плиты E0 в соответствии с рис. 3 определим положение нейтральной оси (х) из условия равенства моментов:
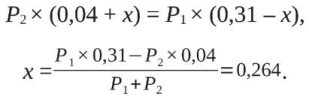
С учетом этого получим:
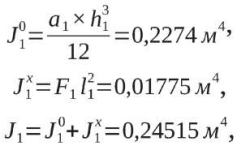
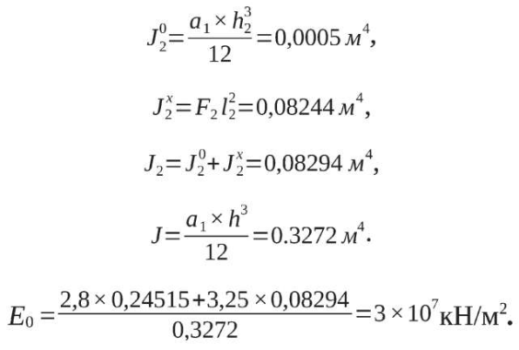
Величину цилиндрической жесткости определим следующим образом:
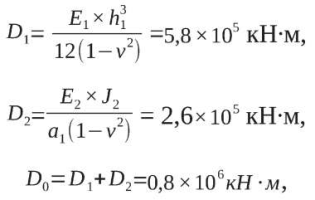
где D0 – осредненное значение цилиндрической жесткости плиты, соответствующее проектным значениям модулей деформации.
В соответствии с [4] частота первого тона собственных колебаний пола при свободном опирании и при m1 = m2 = 1 определяется как:

а в случае жесткого закрепления:
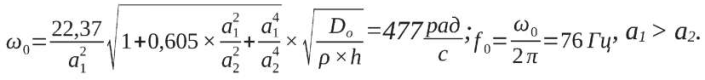
Таким образом, значение частоты собственных колебаний для рассматриваемого пола в системе здания лежит в диапазоне от 38 до 76 Гц для проектных свойств бетона. Частота первого тона собственных колебаний связана с жесткостью плиты соотношением:
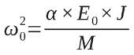 – частота для проектного значения модуля деформации,
– частота для проектного значения модуля деформации,
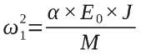 – частота для запроектного значения модуля деформации,
– частота для запроектного значения модуля деформации,
где E'0 – осредненный модуль деформации для запроектного случая;
α – коэффициент жесткости.
Из представленных формул получаем:
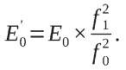
Полученная формула позволяет определить модуль деформации пола, если известна частота собственных колебаний f0 – для проектного случая и частота собственных колебаний f1 – для запроектного случая c учетом старения железобетона. Однако для проектного случая не проводилась вибродиагностика и единственный способ точного определения частоты f0 – это расчет всего здания, так как аналитические формулы дают только диапазон, в котором находится эта частота.
Зная из вибродиагностики значение частоты собственных колебаний пола для запроектного случая (f1 = 37,5 Гц), по вышеприведенной формуле можно получить граничные значения модуля деформации:
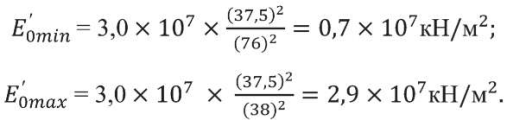
Из табл. 1, соответствующей результатам вибродиагностики, среднее значение модуля деформации для запроектного случая составляет E′0 =1,8×107 кН/м2.
Величина E′0 не выходит за пределы расчетных значений E′0min, E′0max, что характеризует достоверность результатов вибродиагностики.
Таблица 1
Плита перекрытия на отметке +13,450, толщина 0,7 м
Table 1
Intermediate slab at the point +13,450, 0.7 m thick
Измерительный луч в различных частях поверхности конструкции | Скорость рэлеевских волн (м/c) | Эффективная толщина (м) | Скорость продольных волнVp (м/c) | Модуль деформации (кН/м2) |
Луч 1 | 1450 | 0,7 | 2697 | 1,4 × 107 |
Луч 2 | 1800 | 0,5 | 3348 | 2,2 × 107 |
Луч 3 | 1650 | 0,7 | 3069 | 1,8 × 107 |
Луч 4 | 1800 | 0,5 | 3348 | 2,2 × 107 |
Луч 5 | 1400 | 0,7 | 2604 | 1,3 × 107 |
Среднее | 1620 | – | 3013 | 1,8 × 107 |
Далее рассмотрим получение частот собственных колебаний E′0 при различных граничных условиях. Для этого необходимо дополнительно определить коэффициент Пуассона для запроектного случая, так как эта информация не представлена в результатах вибродиагностики.
В соответствии с [5] динамические значения модуля деформации и коэффициента Пуассона в бетоне могут вычисляться через скорости распространения продольных Vp и поперечных волн Vs следующим образом:
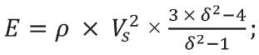 (1)
(1)
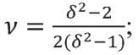 (2)
(2)
где
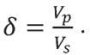 (3)
(3)
Из (2) получим:
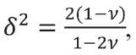
а из (3) получим
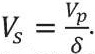
Подставляя полученные выражения в (1), получим следующую связь модуля деформации, скорости продольных волн и коэффициента Пуассона:
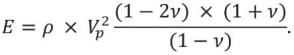
Приводя подобные члены, данное выражение можно свести к уравнению относительно ν следующим образом:
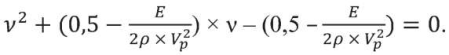
Введя обозначения
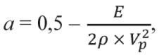
получим следующее квадратное уравнение:
v2 + a × v – a = 0.
Положительное решение данного уравнения имеет вид:
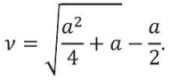
По полученной формуле определим значение коэффициента Пуассона для:
а) запроектных свойств бетона из табл. 1
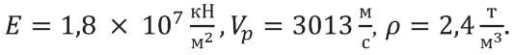
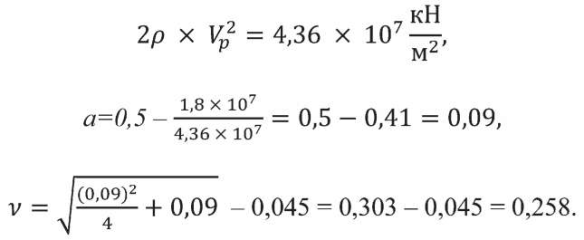
б) проектных свойств бетона E = 3×107 кН/м2, Vp = 3700 м/с, p = 2,4 т/м3.

Как видно, проектное значение коэффициента Пуассона соответствует его нормативной величине, что подтверждает достоверность полученной формулы.
После расчета коэффициента Пуассона для запроектного случая получим осредненное значение цилиндрической жесткости следующим образом:
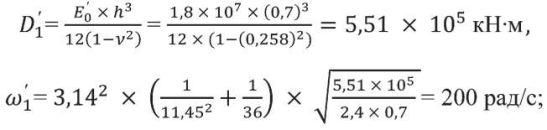
f1′ = 31,8 Гц – частота собственных колебаний плиты для свободно опертых граничных условий,
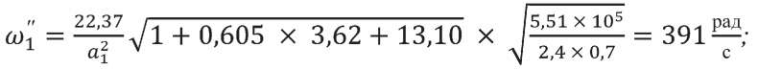
f1′′ = 62,2 – частота собственных колебаний плиты для жестко закрепленных граничных условий.
Следует отметить, что в рассматриваемом случае уточнение коэффициента Пуассона для запроектных свойств бетона не оказало существенного влияния на результаты.
Таким образом, экспериментальное значение частоты собственных колебаний плиты, составляющее 37,5 Гц для запроектного случая, лежит в пределах расчетных значений.
По итогам рассмотрения в табл. 2 представлены результаты сравнительного анализа расчетных и экспериментальных данных.
Таблица 2
Сравнение расчетных и экспериментальных данных
Table 2
Correlation of calculated and experimental data
Модуль деформации пола, Е (кН/м2) | Частота собственных колебаний пола, f (Гц) | |
Расчет для запроектного случая | 0,7 × 107 < Е < 2,9 × 107 | 31,8 < f < 62,2 |
Эксперимент для запроектного случая | Е = 1,8 × 107 | f = 37,5 |
Расчет для проектного случая | Е = 3,0 × 107 | 38 < f < 76 |
Как видно из представленной таблицы:
- экспериментальные значения модуля деформации и частоты собственных колебаний пола не выходят за пределы диапазона расчетных значений;
- проектное значение модуля деформации и частота собственных колебаний претерпели существенное падение из-за возникновения в «горячих» помещениях не предусмотренных проектом трещин в железобетоне.
Оценка НДС и прочности
Далее необходимо провести расчеты НДС здания при действии основных и особых сочетаний нагрузок и воздействий с учетом грунтового основания и с учетом динамических характеристик «горячих» помещений, полученных по результатам вибродиагностики. В результате расчетов формируются расчетные сочетания усилий, по которым определяются результирующие значения НДС и оценивается запас прочности.
Заключение
Представлена методика оценки прочности строительных конструкций действующих АЭС с учетом старения железобетона под воздействием внешних факторов. Методика базируется на неклассическом методе модальной суперпозиции, реализуемой с применением программ для ЭВМ, прошедших аттестацию в Ростехнадзоре, и на вибродиагностике стен и полов «горячих» помещений. В работе также проведена оценка достоверности динамических характеристик, полученных методами вибродиагностики.
В качестве недостатка методики следует отметить отсутствие результатов вибродиагностики по логарифмическим декрементам затуханий и коэффициентам Пуассона.
Список литературы
1. П-01-01-2021 Перечень нормативных правовых актов и нормативных документов, относящихся к сфере деятельности Федеральной службы по экологическому, технологическому и атомному надзору. Раздел I. Технологический, строительный, энергетический надзор. Москва; 2021.
2. АО «Концерн Росэнергоатом». МР 1.5.2.05.999.0025-2011 Расчет и проектирование сейсмостойких атомных станций [Интернет]. Режим доступа: https://eshop.rosenergoatom.ru/downloadable/download/linkSample/link_id/1622/
3. Коротков В.А., Кузьминов А.В., Родин П.А. Учет «грунтового» демпфера в методе модальной суперпозиции при динамическом расчете строительных конструкций АЭС. Сейсмостойкое строительство. Безопасность сооружений. 2022;(3):20–30. https://doi.org/10.37153/2618-9283-2022-3-20-30
4. Биргер И. А., Пановко Я.Г., ред. Расчет конструкций на сейсмостойкость. Том 3. Москва: Машиностроение; 1968.
5. Бирбраер А.Н. Расчет конструкций на сейсмостойкость. Санкт-Петербург: Наука; 1988.
Об авторах
А. В. ЕсеновРоссия
Амра Владимирович Есенов, канд. техн. наук, заместитель начальника отдела надежности строительных конструкций
107140, г. Москва, ул. Малая Красносельская, д. 2/8, к. 5
В. А. Коротков
Россия
Владимир Анатольевич Коротков, канд. техн. наук, ведущий научный сотрудник отдела надежности строительных конструкций
107140, г. Москва, ул. Малая Красносельская, д. 2/8, к. 5
А. В. Кузьминов
Россия
Александр Владимирович Кузьминов, старший научный сотрудник отдела надежности строительных конструкций
107140, г. Москва, ул. Малая Красносельская, д. 2/8, к. 5
П. А. Родин
Россия
Павел Александрович Родин, младший научный сотрудник отдела надежности строительных конструкций
107140, г. Москва, ул. Малая Красносельская, д. 2/8, к. 5
тел.: +7 (499) 264-40-45
Н. М. Сидоров
Россия
Никита Маркович Сидоров, младший научный сотрудник отдела надежности строительных конструкций
107140, г. Москва, ул. Малая Красносельская, д. 2/8, к. 5
Т. З. Югай
Россия
Тамара Захаровна Югай, старший научный сотрудник отдела надежности строительных конструкций
107140, г. Москва, ул. Малая Красносельская, д. 2/8, к. 5
Рецензия
Для цитирования:
Есенов А.В., Коротков В.А., Кузьминов А.В., Родин П.А., Сидоров Н.М., Югай Т.З. Оценка прочности и устойчивости железобетонных конструкций АЭС с учетом результатов вибродиагностики. Вестник НИЦ «Строительство». 2022;34(3):79-91. https://doi.org/10.37538/2224-9494-2022-3(34)-79-91
For citation:
Esenov A.V., Korotkov V.A., Kuzminov A.V., Rodin P.A., Sidorov N.M., Yugai T.Z. Strength and stability assessment of NPP reinforced concrete structures regarding the results of vibration analysis. Bulletin of Science and Research Center of Construction. 2022;34(3):79-91. (In Russ.) https://doi.org/10.37538/2224-9494-2022-3(34)-79-91


























