Перейти к:
Определение критического значения частоты собственных колебаний и модуля деформации железобетонных строительных конструкций для динамического мониторинга
https://doi.org/10.37538/2224-9494-2025-3(46)-62-74
EDN: IYVTTR
Аннотация
Введение. Статья является продолжением работ по учету в анализе с помощью вибродиагностики динамических характеристик строительных конструкций зданий, содержащих трещины в бетоне. Разработанные ранее авторами методики позволили сделать оценку ослабления жесткости и уменьшения частоты собственных колебаний в элементах строительных конструкций, а далее определить критическое значение частоты и соответствующего модуля деформации, по достижении которых дальнейшая эксплуатация здания невозможна. Дано описание оригинального подхода определения критического значения частоты собственных колебаний и соответствующего модуля деформации бетона.
Цель. Определение критической частоты собственных колебаний фрагмента здания (перекрытие/стена), по достижении которой дальнейшая эксплуатация здания невозможна.
Материалы и методы. На конкретных примерах получены значения критической частоты собственных колебаний и соответствующее значение модуля деформации перекрытия и стены. Рассмотрено влияние комбинированных граничных условий (сочетание шарнирных опор и жесткой заделки) на частоты собственных колебаний различных строительных конструкций.
Результаты. Полученные результаты расчетов с учетом вибродиагностики для перекрытия характеризуются запасом прочности и несущей способности, а для стены прочность обеспечена, но запас по несущей способности незначительный.
Выводы. Преимуществом предлагаемого подхода, по сравнению с изложенным в методике МЧС, является расчет критического значения частоты собственных колебаний и модуля деформации бетона строительных конструкций зданий.
Ключевые слова
Для цитирования:
Коротков В.А., Родин П.А. Определение критического значения частоты собственных колебаний и модуля деформации железобетонных строительных конструкций для динамического мониторинга. Вестник НИЦ «Строительство». 2025;46(3):62-74. https://doi.org/10.37538/2224-9494-2025-3(46)-62-74. EDN: IYVTTR
For citation:
Korotkov V.A., Rodin P.A. Calculating the critical value of the natural frequency and deformation modulus of reinforced concrete structures for dynamic monitoring. Bulletin of Science and Research Center of Construction. 2025;46(3):62-74. (In Russ.) https://doi.org/10.37538/2224-9494-2025-3(46)-62-74. EDN: IYVTTR
В соответствии с [1] рассмотрим методику решения задачи на примере расчета критической частоты собственных колебаний перекрытия здания, которое моделировалось прямоугольной пластиной. В расчетах автономной пластины учитывались два вида граничных условий – шарнирно опертые и жестко защемленные граничные условия [2], так как в пределах этих границ находится интересуемая частота.
Модальный анализ проводился по программе ЛОГОС1.
Исходные данные для расчета имеют вид (материал 1):
– длина а1 = 11,45 м; ширина а2 = 6 м; толщина h = 0,7 м;
– модуль Юнга Eпроект1 = 3 × 10⁷ кН/м² (проектный модуль деформации бетона класса В22,5);
– коэффициент Пуассона ν = 0,2;
– массовая плотность ρ = 2,4 т/м³.
Цилиндрическая жесткость определялась по формуле:
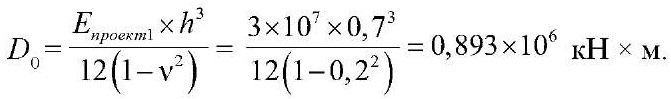
Частоту собственных колебаний шарнирно опертой по контуру прямоугольной пластины можно определить по следующей аналитической формуле [3]:
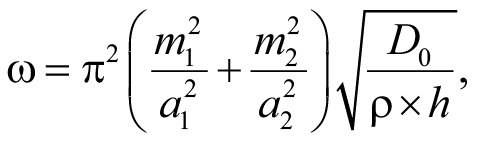
где m1 и m2 – целые числа, соответствующие номеру тона колебаний. В результате было получено аналитическое значение частоты собственных колебаний первого тона:
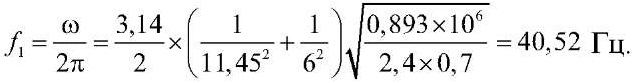
Расчеты по программе выполнялись сначала для сетки КЭ 10 × 10, а затем для сетки КЭ 20 × 20, что оказалось достаточным для сходимости решения.
В табл. 1 представлена оценка частоты собственных колебаний перекрытия, полученная аналитическим путем и по программе.
Таблица 1
Оценка частоты собственных колебаний перекрытия
Table 1
Assessment of the natural frequency of the slab
Частота, Гц | Аналитика | Расчет по программе (20 × 20) | Погрешность |
f1 | 40,52 Гц | 39,54 Гц | 2,4 % |
Погрешность расчета 2,4 % является приемлемой.
На рис. 1 представлена форма колебаний первого тона.
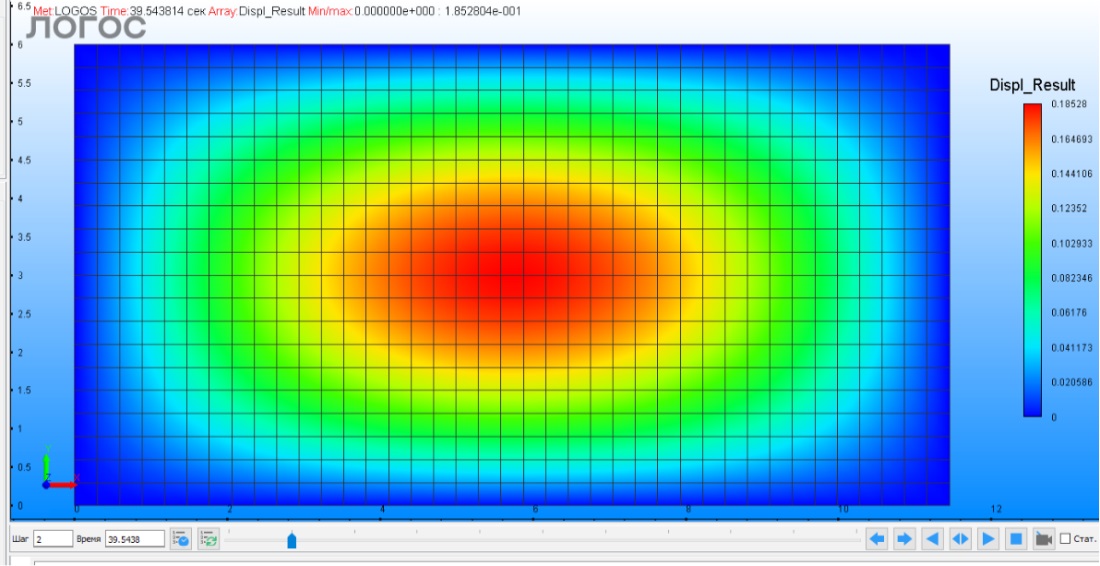
Рис. 1. Частота и форма собственных колебаний первого тона
Fig. 1. Frequency and shape of natural frequency of the first mode
Далее рассмотрим модель перекрытия, но с учетом арматуры, имеющей следующие свойства (материал 2):
− модуль Юнга Eпроект2 = 2 × 10⁸ кН/м² (проектный модуль деформации арматуры);
− коэффициент Пуассона ν = 0,3;
− массовая плотность ρ = 7,85 т/м³.
Бетон с арматурой моделировались в виде многослойного КЭ [4], состоящего из пяти слоев, показанных на рис. 2, где материал 1 соответствует бетону, а материал 2 соответствует стальной арматуре.
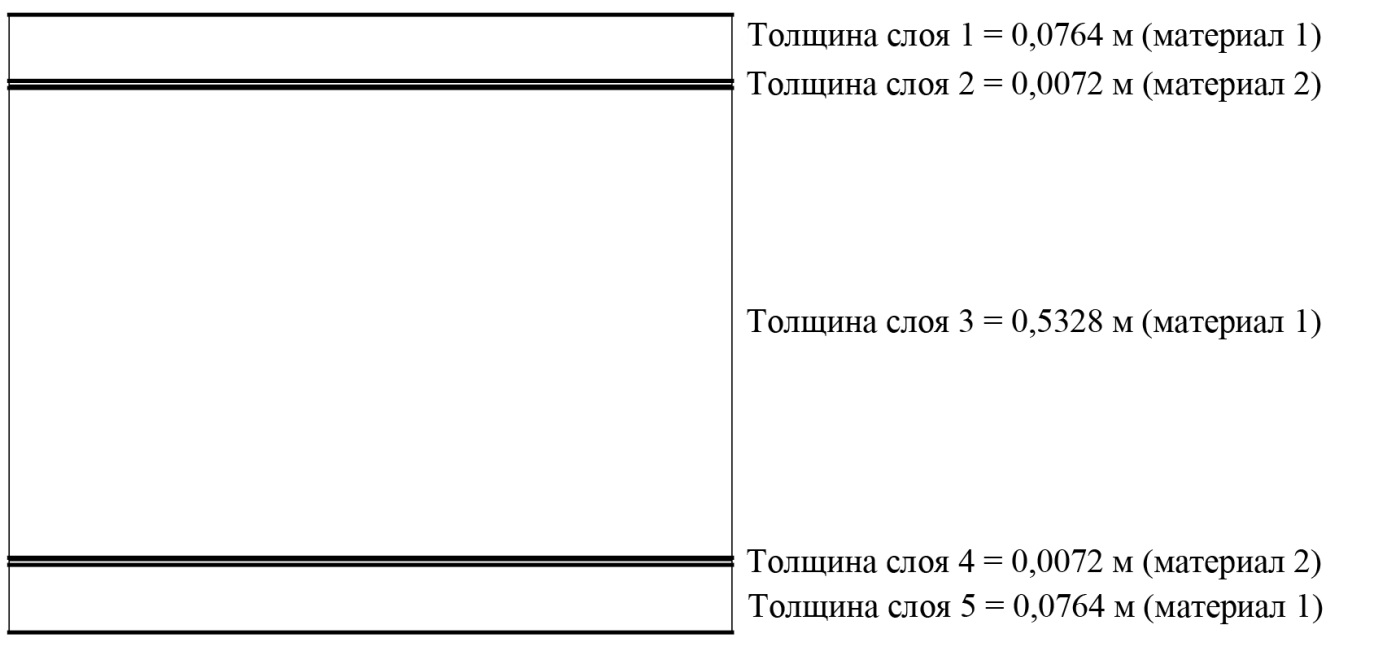
Рис. 2. Слоистая модель перекрытия из бетона и арматуры толщиной 0,7 м
Fig. 2. Layered model of a concrete and reinforcement slab with a 0.7 m thickness
В работе выполнялась серия расчетов частоты собственных колебаний плиты при уменьшении модуля деформации бетона от проектного до нулевого значения, соответствующего полностью разрушенному бетону. При этом учитывались инерционные свойства бетона и арматуры, которые считались неизменными во всех расчетах. Модуль деформации арматуры учитывался по двум сценариям. По сценарию жб1 модуль деформации арматуры оставался неизменным при деградации модуля деформации бетона от нормативного до нулевого значения, а по сценарию жб2 модули деформации бетона и арматуры одновременно уменьшались от нормативных до нулевых значений. Графики зависимости частоты собственных колебаний первого тона от модуля деформации бетона и железобетона в относительных единицах представлены на рис. 3, а оцифровка графиков представлена в табл. 2.
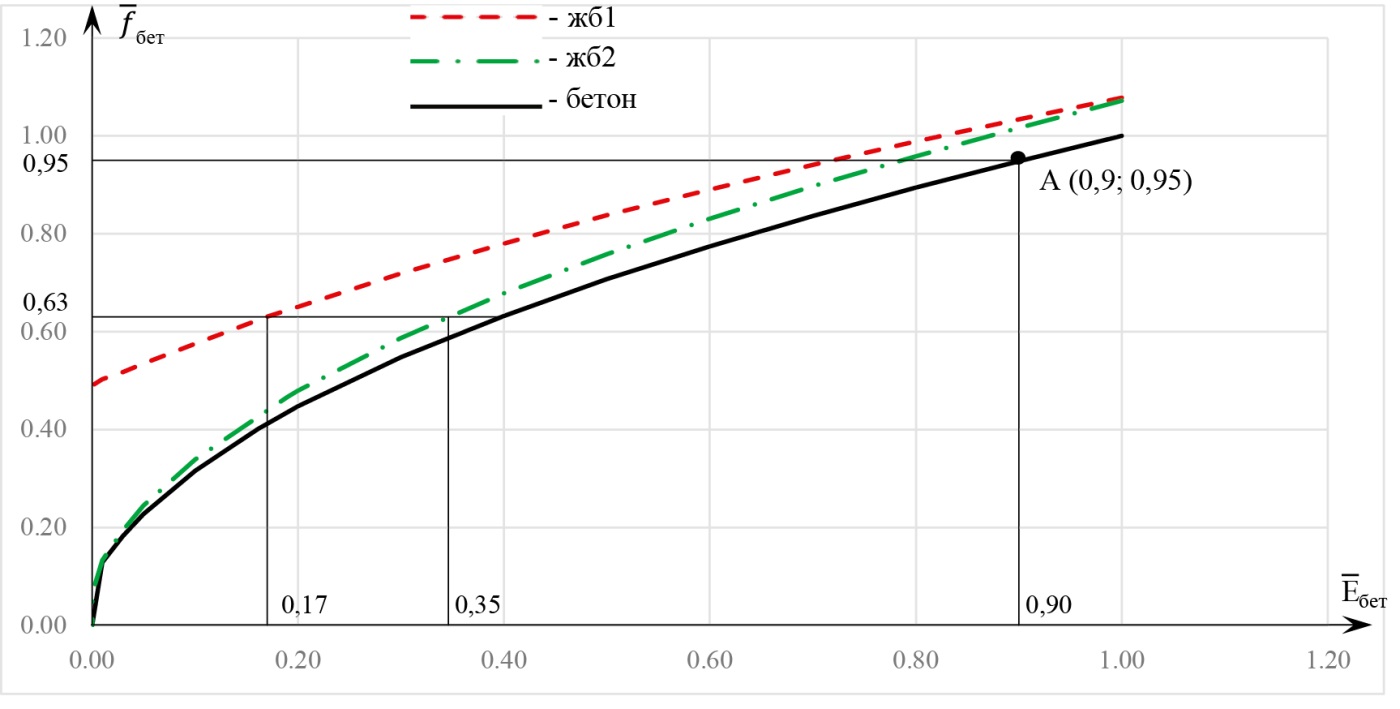
Рис. 3. Зависимость частоты собственных колебаний от модуля деформации перекрытия (шарнирное опирание)
Fig. 3. Relation between natural frequency and deformation modulus of the slab (hinged support)
Таблица 2
Сравнение частот собственных колебаний перекрытия из бетона и железобетона (шарнирно опертая плита)
Table 2
Comparison of natural frequencies of concrete and reinforced concrete slabs (hinge-supported slab)
№ п/п | Ебет = Еарм | Ебет, кН/м² | Еарм, кН/м² | fжб1, Гц | fжб2, Гц | fбет, Гц | fбет | fжб1 | fжб2 |
1 | 1,00 | 3,00 × 10⁷ | 2,00 × 10⁸ | 42,62 | 42,37 | 39,54 | 1,00 | 1,08 | 1,07 |
2 | 0,90 | 2,70 × 10⁷ | 1,80 × 10⁸ | 40,89 | 40,20 | 37,51 | 0,95 | 1,03 | 1,02 |
3 | 0,80 | 2,40 × 10⁷ | 1,60 × 10⁸ | 39,09 | 37,90 | 35,36 | 0,89 | 0,99 | 0,96 |
4 | 0,70 | 2,10 × 10⁷ | 1,40 × 10⁸ | 37,20 | 35,45 | 33,08 | 0,84 | 0,94 | 0,90 |
5 | 0,60 | 1,80 × 10⁷ | 1,20 × 10⁸ | 35,21 | 32,82 | 30,63 | 0,77 | 0,89 | 0,83 |
6 | 0,50 | 1,50 × 10⁷ | 1,00 × 10⁸ | 33,10 | 29,96 | 27,96 | 0,71 | 0,84 | 0,76 |
7 | 0,40 | 1,20 × 10⁷ | 0,80 × 10⁸ | 30,85 | 26,80 | 25,00 | 0,63 | 0,78 | 0,68 |
8 | 0,30 | 0,90 × 10⁷ | 0,60 × 10⁸ | 28,41 | 23,21 | 21,65 | 0,55 | 0,72 | 0,59 |
9 | 0,20 | 0,60 × 10⁷ | 0,40 × 10⁸ | 25,74 | 18,95 | 17,68 | 0,45 | 0,65 | 0,48 |
10 | 0,17 | 0,57 × 10⁷ | 0,38 × 10⁸ | 24,91 | 18,47 | 15,81 | 0,40 | 0,63 | 0,47 |
11 | 0,10 | 0,30 × 10⁷ | 0,20 × 10⁸ | 22,74 | 13,40 | 12,50 | 0,32 | 0,58 | 0,34 |
12 | 0,05 | 0,15 × 10⁷ | 0,10 × 10⁸ | 21,17 | 9,67 | 9,00 | 0,23 | 0,54 | 0,24 |
13 | 0,03 | 0,10 × 10⁷ | 0,06 × 10⁸ | 20,48 | 7,66 | 7,21 | 0,18 | 0,52 | 0,19 |
14 | 0,01 | 0,05 × 10⁷ | 0,02 × 10⁸ | 19,87 | 5,25 | 5,10 | 0,13 | 0,50 | 0,13 |
15 | 0,00 | 0,01 × 10⁷ | 0,01 × 10⁸ | 19,37 | 2,56 | 0,00 | 0,00 | 0,49 | 0,06 |
Ниже приводится список принятых обозначений:
Епроект1 – проектное значение модуля деформации бетона;
Епроект2 – проектное значение модуля деформации арматуры;
Ебет – текущее значение модуля деформации бетона от проектной до нулевой величины;
Еарм – текущее значение модуля деформации арматуры от проектной до нулевой величины;
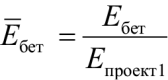 – относительное значение модуля деформации бетона;
– относительное значение модуля деформации бетона;
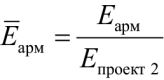 – относительное значение модуля деформации арматуры;
– относительное значение модуля деформации арматуры;
fбет – частота собственных колебаний перекрытия из бетона для текущих значений модуля деформации бетона;
fжб1 – частота собственных колебаний перекрытия из железобетона для текущих значений модуля деформации бетона и арматуры (сценарий жб1);
fжб2 – частота собственных колебаний перекрытия из железобетона для текущих значений модуля деформации бетона и арматуры (сценарий жб2);
fпроект = 39,54 Гц – проектное значение частоты собственных колебаний перекрытия из проектного бетона при шарнирном опирании и fпроект = 73,65 Гц в расчете на жесткой заделке;
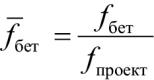 – относительное значение частоты собственных колебаний перекрытия из бетона;
– относительное значение частоты собственных колебаний перекрытия из бетона;
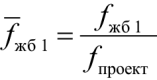 – относительное значение частоты собственных колебаний перекрытия из железобетона (сценарий жб1);
– относительное значение частоты собственных колебаний перекрытия из железобетона (сценарий жб1);
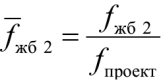 – относительное значение частоты собственных колебаний перекрытия из железобетона (сценарий жб2).
– относительное значение частоты собственных колебаний перекрытия из железобетона (сценарий жб2).
Как видно из рис. 3, при уменьшении модуля деформации бетона от проектных до нулевых значений частота собственных колебаний перекрытия снижается. Точкой А на рис. 3 отмечено экспериментальное (вибродиагностика) значение частоты собственных колебаний перекрытия 37,6 Гц, которое соответствует модулю деформации бетона 0,9Епроект1.
Для проектного значения модуля деформации частота собственных колебаний перекрытия из железобетона на 7,7 % превосходит частоту собственных колебаний перекрытия из бетона за счет влияния арматуры. При значении модуля деформации бетона, близком к нулю (полностью разрушенный бетон), значение частоты собственных колебаний перекрытия составило 19,24 Гц. Эта частота соответствует катастрофической (аварийной) степени повреждения рассматриваемого перекрытия и определяется на основании жесткости арматуры и инерционных свойств арматуры и бетона.
Для оценки критической частоты принимается подход, изложенный в таблице 9 методики МЧС [5]. Согласно данному подходу, при уменьшении квадрата частоты собственных колебаний конструкции на 60 % конструкция переходит из сильно ограниченно-работоспособного технического состояния в тяжелое аварийное техническое состояние. Уменьшению квадрата частоты собственных колебаний конструкции на 60 % соответствует значение самой частоты, составляющее 63 % от ее проектного значения. Как видно из рис. 3, для такого технического состояния перекрытия частота собственных колебаний, составляющая 0,63 от ее проектного значения, в зависимости от сценария лежит в диапазоне модулей деформации бетона от 0,17 до 0,35 первоначального значения.
Далее рассмотрим аналогичное решение по определению критического значения частоты собственных колебаний перекрытия, но с жестко защемленными граничными условиями [6]. Частоту собственных колебаний пластины можно определить по следующей формуле:
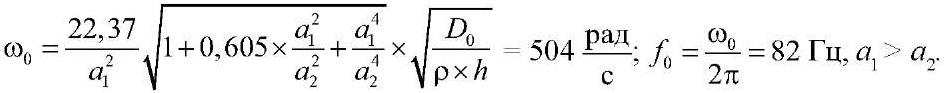
Погрешность при сравнении полученного результата с расчетом по программе ЛОГОС составила 10 %.
На рис. 4 и в табл. 3 представлены результаты расчетов, которые выполнены в той же постановке, как и в случае шарнирного опирания перекрытия.
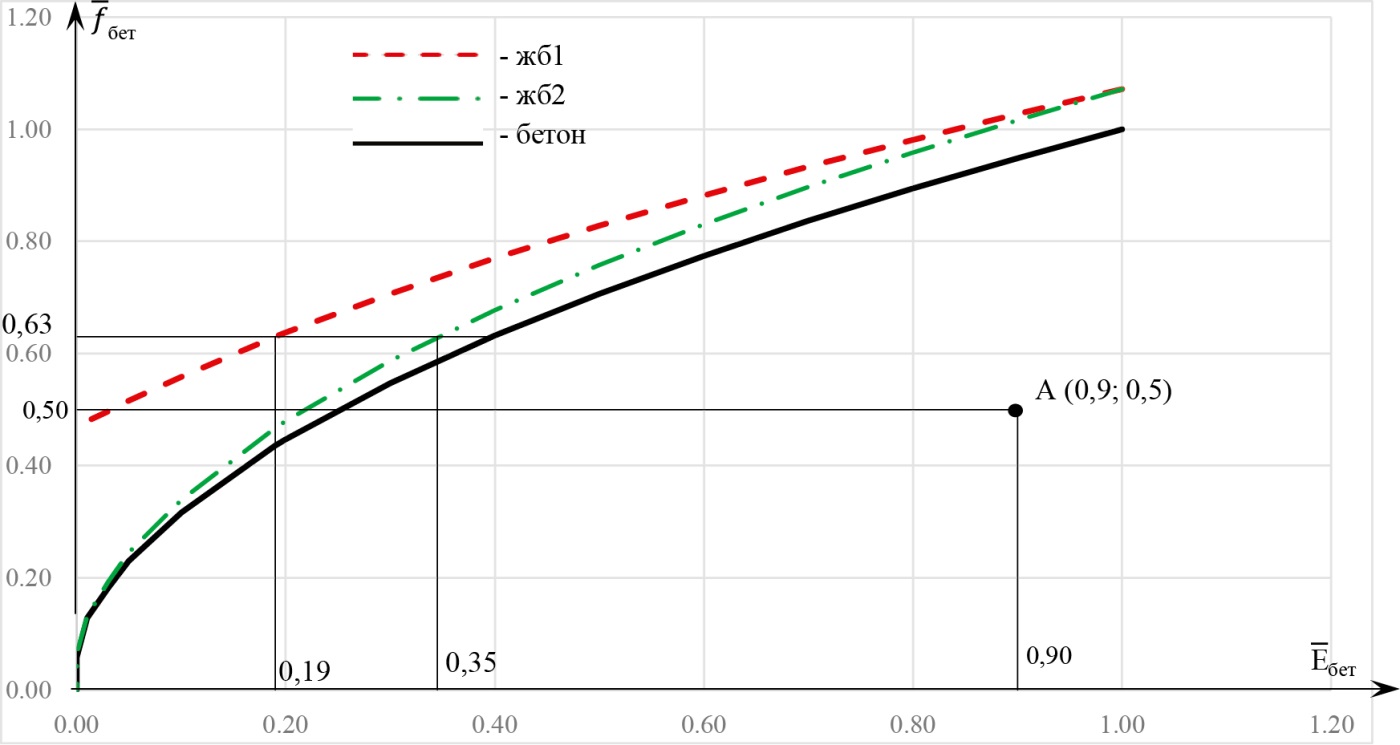
Рис. 4. Зависимость относительной частоты собственных колебаний от относительного значения модуля деформации перекрытия (жесткая заделка)
Fig. 4. Relation between the relative frequency of natural frequency and the relative value of the deformation modulus of the slab (rigid fixing)
Таблица 3
Сравнение частот собственных колебаний перекрытия из бетона и железобетона (жесткое защемление)
Table 3
Comparison of natural frequencies of concrete and reinforced concrete slabs (rigid fixing)
№ п/п | Ебет = Еарм | Ебет, кН/м² | Еарм, кН/м² | fжб1, Гц | fжб2, Гц | fбет, Гц | fбет | fжб1 | fжб2 |
1 | 1,00 | 3,00 × 10⁷ | 2,00 × 10⁸ | 78,93 | 78,93 | 73,65 | 1,00 | 1,07 | 1,07 |
2 | 0,90 | 2,70 × 10⁷ | 1,80 × 10⁸ | 75,69 | 74,88 | 69,87 | 0,95 | 1,03 | 1,02 |
3 | 0,80 | 2,40 × 10⁷ | 1,60 × 10⁸ | 72,30 | 70,60 | 65,87 | 0,89 | 0,98 | 0,96 |
4 | 0,70 | 2,10 × 10⁷ | 1,40 × 10⁸ | 68,75 | 66,04 | 61,62 | 0,84 | 0,93 | 0,90 |
5 | 0,60 | 1,80 × 10⁷ | 1,20 × 10⁸ | 64,99 | 61,14 | 57,05 | 0,77 | 0,88 | 0,83 |
6 | 0,50 | 1,50 × 10⁷ | 1,00 × 10⁸ | 61,00 | 55,81 | 52,08 | 0,71 | 0,83 | 0,76 |
7 | 0,40 | 1,20 × 10⁷ | 0,80 × 10⁸ | 56,72 | 49,92 | 46,58 | 0,63 | 0,77 | 0,68 |
8 | 0,30 | 0,90 × 10⁷ | 0,60 × 10⁸ | 52,08 | 43,23 | 40,34 | 0,55 | 0,71 | 0,59 |
9 | 0,20 | 0,60 × 10⁷ | 0,40 × 10⁸ | 46,95 | 35,30 | 32,93 | 0,45 | 0,64 | 0,48 |
10 | 0,19 | 0,57 × 10⁷ | 0,38 × 10⁸ | 46,40 | 34,40 | 32,10 | 0,44 | 0,63 | 0,47 |
11 | 0,10 | 0,30 × 10⁷ | 0,20 × 10⁸ | 41,11 | 24,96 | 23,29 | 0,32 | 0,56 | 0,34 |
12 | 0,05 | 0,15 × 10⁷ | 0,10 × 10⁸ | 37,98 | 18,02 | 16,90 | 0,23 | 0,52 | 0,24 |
13 | 0,03 | 0,10 × 10⁷ | 0,06 × 10⁸ | 36,60 | 14,27 | 13,44 | 0,18 | 0,50 | 0,19 |
14 | 0,01 | 0,05 × 10⁷ | 0,02 × 10⁸ | 35,35 | 9,78 | 9,50 | 0,13 | 0,48 | 0,13 |
15 | 0,00 | 0,01 × 10⁷ | 0,01 × 10⁸ | 34,30 | 4,77 | 4,25 | 0,06 | 0,47 | 0,06 |
По результатам рассмотрения можно заключить, что критическая частота собственных колебаний перекрытия лежит в диапазоне модулей деформации перекрытия от 0,19 до 0,35 от проектного модуля деформации бетона, что обеспечивает слишком консервативный характер результатов при расчете перекрытия на жесткой заделке. Решение для перекрытия на шарнирных опорах находится в лучшем соответствии с экспериментальным результатом, полученным из вибродиагностики в точке А. Ввиду этого итоговое значение критической частоты собственных колебаний для данного перекрытия составит 24,9 Гц при модуле деформации бетона 0,5 × 10⁷ кН/м² и при шарнирном опирании, что соответствует сценарию жб1, когда по мере деградации модуля деформации бетона от проектного до нулевого значения модуль деформации арматуры не претерпевает существенных изменений.
Следует отметить, что при колебаниях в упругой области изгибная жесткость железобетонного перекрытия определяется из расчета относительно нейтральной оси, проходящей через центр сечения, а при колебаниях в неупругой области нейтральная ось смещается, что оказывает влияние на результат. Опосредованный учет этого производится за счет рассмотрения в модальном анализе всех возможных жесткостей перекрытия в диапазоне от проектного до нулевых значений.
Для расширения методики, изложенной в [1], дополнительно рассмотрим расчет критической частоты собственных колебаний стены здания, которая также моделировалась прямоугольной пластиной. В расчетах автономной пластины учитывались два вида граничных условий – жестко защемленные и комбинированные (шарнирно опертые по контуру, жесткая заделка снизу). Применение комбинированных граничных условий обусловлено примыканием массивной фундаментной плиты к нижней части данной стены, что обеспечивает хорошее соответствие с результатами вибродиагностики.
Исходные данные для расчета имеют вид (материал 1):
– длина а1 = 21,8 м; ширина а2 = 4,7 м; толщина h1 = 2,1 м; h2 = 0,9 м;
– модуль Юнга Eпроект1 = 3 × 10⁷ кН/м² (проектный модуль деформации бетона класса В22,5);
– коэффициент Пуассона ν = 0,2;
– массовая плотность ρ = 2,4 т/м³.
Геометрические размеры стены приведены на рис. 5.
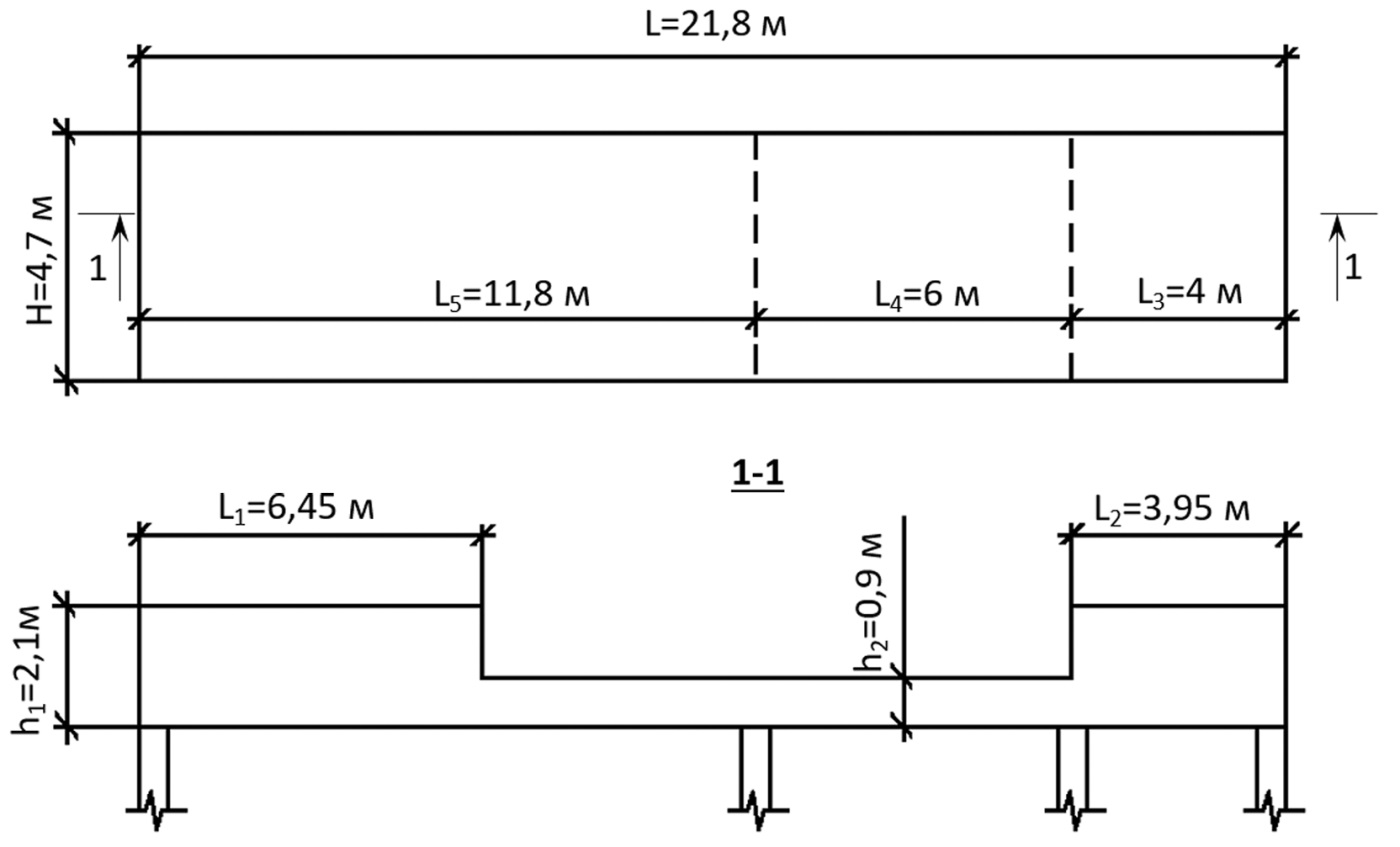
Рис. 5. Геометрические размеры стены
Fig. 5. Geometric dimensions of the wall
На рис. 5 пунктирной линией показаны места примыкания поперечных стен, которые учитывались наложенными связями в нормальном к стене направлении. Железобетонная стена моделировались с помощью многослойных КЭ, состоящих из пяти слоев, показанных на рис. 6 и 7.
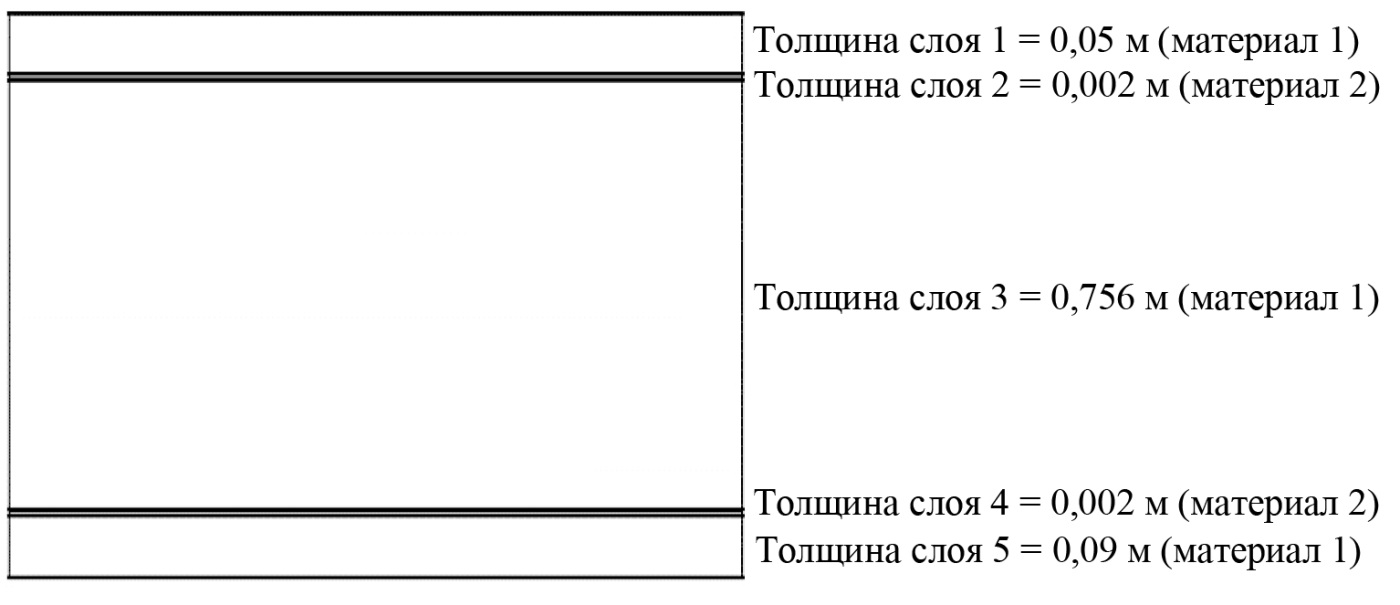
Рис. 6. Многослойный КЭ толщиной 0,9 м
Fig. 6. Multilayer finite element with a thickness of 0.9 m
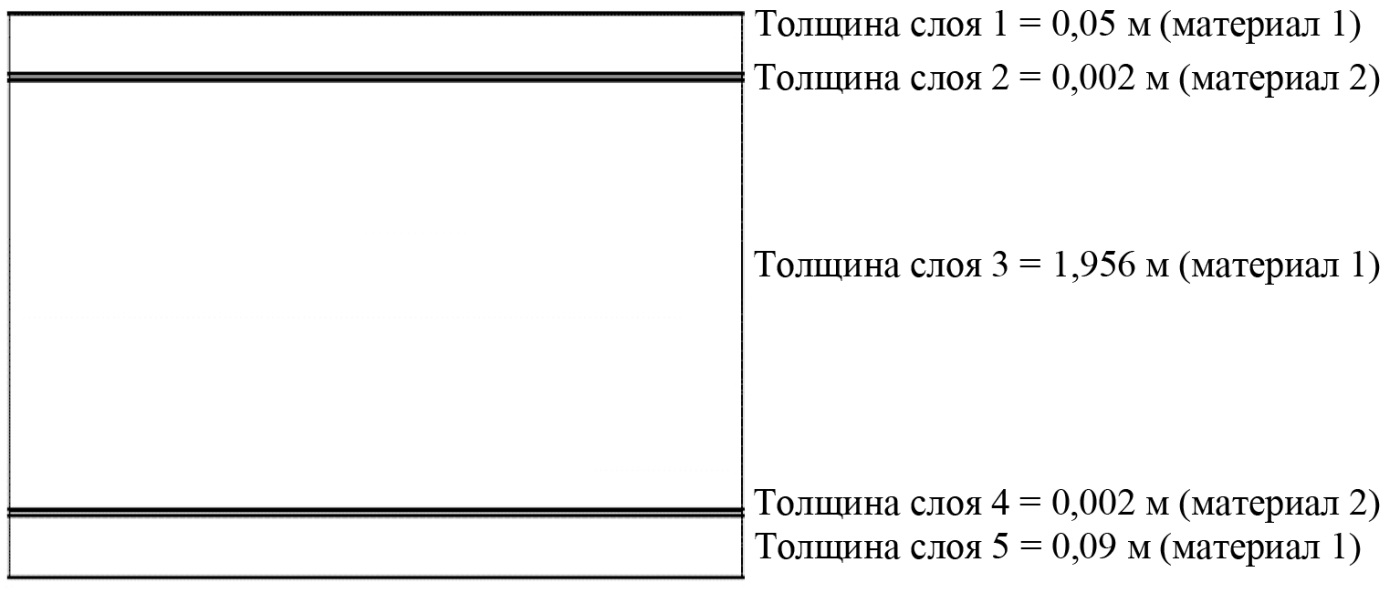
Рис. 7. Многослойный КЭ толщиной 2,1 м
Fig. 7. Multilayer finite element with a thickness of 2.1 m
На рис. 8 показан первый тон собственных колебаний стены для шарнирного опирания по контуру + жесткая заделка снизу.
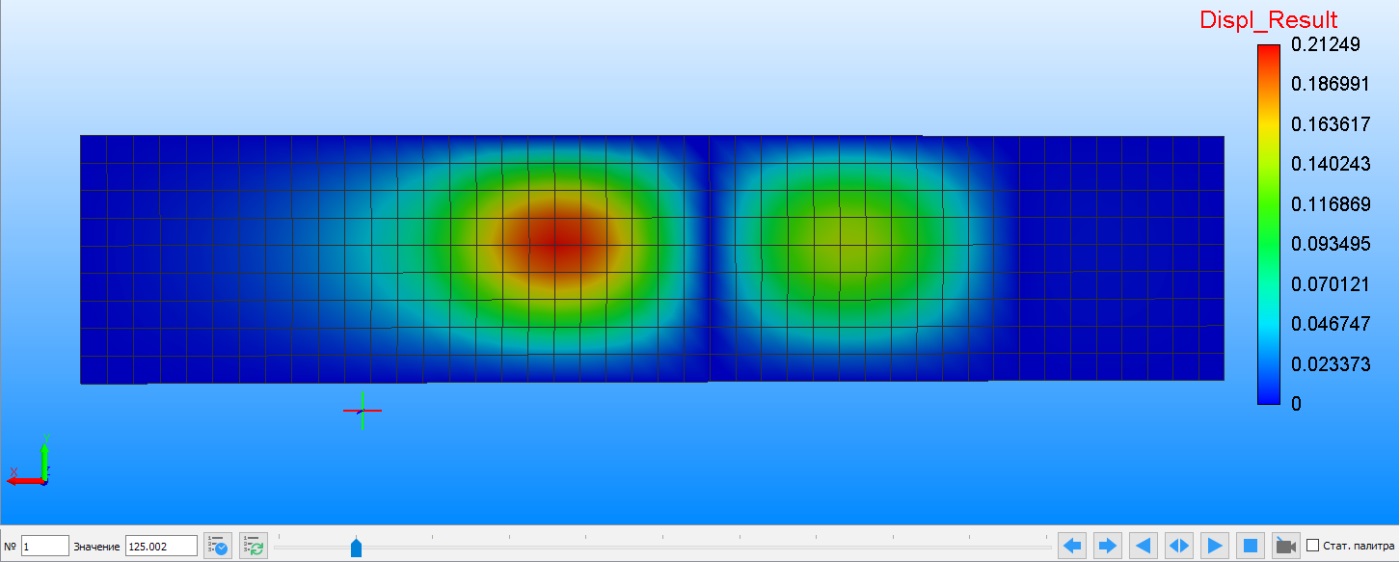
Рис. 8. Первый тон собственных колебаний стены для шарнирного опирания по контуру + жесткая заделка снизу
Fig. 8. First mode of the natural frequency of wall for hinged support along the perimeter + rigid fixing from below
В табл. 4 и на рис. 9 представлены графики зависимости частоты собственных колебаний стены от модуля деформации бетона и арматуры и их оцифровка.
Таблица 4
Сравнение частот собственных колебаний стены из бетона и железобетона (шарнирное опирание по контуру + жесткая заделка снизу)
Table 4
Comparison of natural frequencies of concrete and reinforced concrete walls (hinged support along the perimeter + rigid fixing from below)
№ п/п | Ебет = Еарм | Ебет, кН/м² | Еарм, кН/м² | fжб1, Гц | fжб2, Гц | fбет, Гц | fбет | fжб1 | fжб2 |
1 | 1,00 | 3,00 × 10⁷ | 2,00 × 10⁸ | 125,0 | 125,0 | 122,8 | 1,00 | 1,02 | 1,02 |
2 | 0,90 | 2,70 × 10⁷ | 1,80 × 10⁸ | 118,7 | 118,4 | 116,3 | 0,95 | 0,97 | 0,96 |
3 | 0,80 | 2,40 × 10⁷ | 1,60 × 10⁸ | 112,1 | 111,3 | 109,4 | 0,89 | 0,91 | 0,91 |
4 | 0,70 | 2,10 × 10⁷ | 1,40 × 10⁸ | 105,0 | 103,8 | 102,0 | 0,83 | 0,85 | 0,85 |
5 | 0,60 | 1,80 × 10⁷ | 1,20 × 10⁸ | 98,4 | 96,8 | 95,1 | 0,77 | 0,80 | 0,79 |
6 | 0,50 | 1,50 × 10⁷ | 1,00 × 10⁸ | 90,6 | 88,4 | 86,9 | 0,71 | 0,74 | 0,72 |
7 | 0,40 | 1,20 × 10⁷ | 0,80 × 10⁸ | 82,0 | 79,1 | 77,7 | 0,63 | 0,67 | 0,64 |
8 | 0,35 | 1,02 × 10⁷ | 0,70 × 10⁸ | 77,1 | 73,8 | 72,5 | 0,59 | 0,63 | 0,60 |
9 | 0,30 | 0,90 × 10⁷ | 0,60 × 10⁸ | 72,3 | 68,5 | 67,3 | 0,55 | 0,59 | 0,56 |
10 | 0,20 | 0,60 × 10⁷ | 0,40 × 10⁸ | 61,1 | 55,9 | 54,9 | 0,45 | 0,50 | 0,46 |
11 | 0,10 | 0,30 × 10⁷ | 0,20 × 10⁸ | 47,2 | 39,5 | 38,8 | 0,32 | 0,38 | 0,32 |
12 | 0,05 | 0,15 × 10⁷ | 0,10 × 10⁸ | 38,3 | 28,4 | 27,9 | 0,23 | 0,31 | 0,23 |
13 | 0,01 | 0,02 × 10⁷ | 0,05 × 10⁸ | 26,3 | 13,0 | 12,3 | 0,10 | 0,21 | 0,11 |
14 | 0,005 | 0,01 × 10⁷ | 0,01 × 10⁸ | 24,0 | 9,0 | 8,8 | 0,07 | 0,20 | 0,07 |
15 | 0,001 | 0,002 × 10⁷ | 0,005 × 10⁸ | 21,6 | 4,1 | 3,9 | 0,03 | 0,18 | 0,03 |
16 | 0,00 | 1,00 | 1,00 | 21,0 | 0,0 | 0,0 | 0,00 | 0,17 | 0,00 |
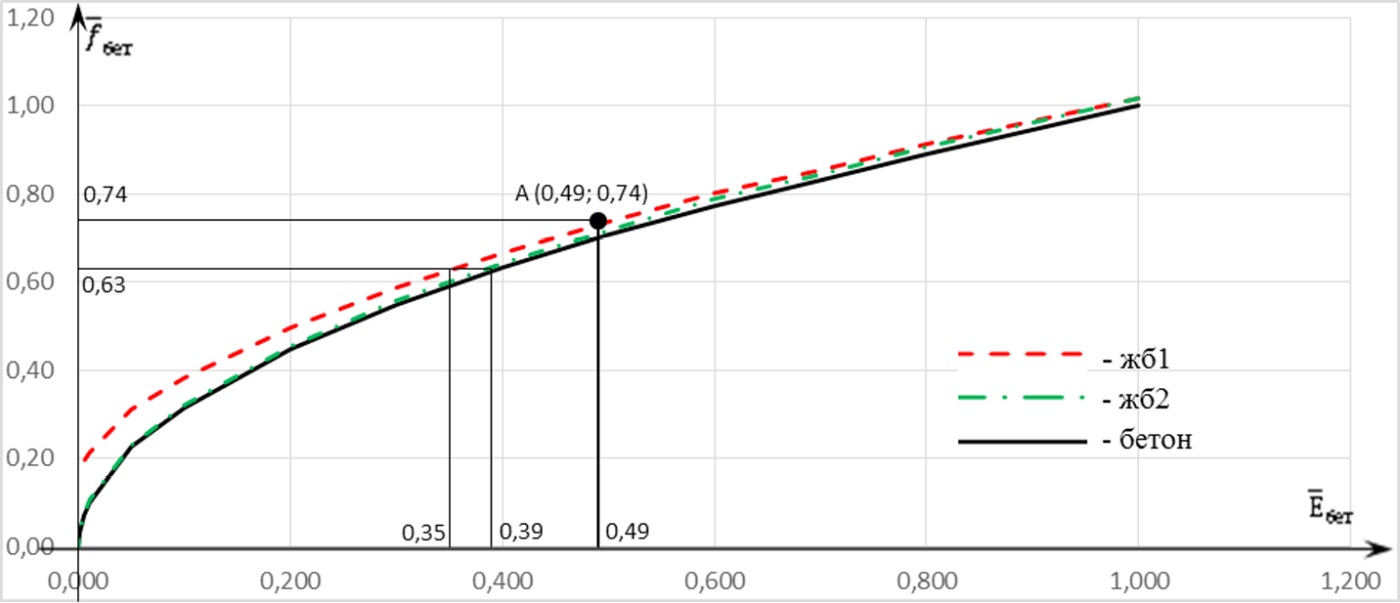
Рис. 9. Зависимость относительной частоты собственных колебаний от относительного значения модуля деформации стены (шарнирное опирание по контуру + жесткая заделка снизу)
Fig. 9. Relation between the relative frequency of natural frequency and the relative value of wall deformation modulus (hinged support along the perimeter + rigid fixing from below)
Для верификации представленного подхода необходимо провести нелинейный анализ системы «сооружение – грунтовое основание» с учетом работы железобетонного перекрытия.
Выводы
В работе представлено обоснование критерия для динамического мониторинга строительных конструкций, основанного на модальном анализе, на методике МЧС, разработанной для зданий, и на результатах вибродиагностики.
По результатам выполненных расчетов получили:
– для перекрытия на отметке +13,6 критическое значение частоты собственных колебаний составило 0,63 в долях от проектного значения, а экспериментальное значение – 0,95, что характеризует существенный запас по несущей способности; катастрофическое значение частоты для перекрытия составило 0,49;
– для стены критическое значение частоты собственных колебаний составило 0,63, а экспериментальное значение – 0,74, что также обеспечивает запас по несущей способности, так как превышает критическое значение; катастрофическое значение частоты для стены НВК составило 0,17;
– для критических значений частот собственных колебаний перекрытия и стены соответствующие значения модулей деформации составили 0,17 и 0,35 в долях от проектного значения модуля деформации бетона.
1. Пакет программ для ЭВМ «ЛОГОС», версия 5 (ЛОГОС-ПРОЧНОСТЬ), ФГУП «РФЯЦ-ВНИИЭФ», РФ.
Список литературы
1. ГОСТ 27751-2014. Надежность строительных конструкций и оснований. Основные положения. Москва: Стандартинформ; 2015.
2. ГОСТ Р ИСО 2394-2016. Конструкции строительные. Основные принципы надежности. Москва: Стандартинформ; 2016.
3. EN 1990:2002+A1. Eurocode – Basis of structural design [internet]. Brussels : Management Centre; 2002. Available at: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1990.2002.pdf.
4. СП 385.1325800.2018. Защита зданий и сооружений от прогрессирующего обрушения. Правила проектирования. Основные положения. Москва: Стандартинформ; 2018.
5. СП 296.1325800.2017. Здания и сооружения. Особые воздействия (с Изменением N 1) [интернет]. Режим доступа: https://docs.cntd.ru/document/555600219 (дата обращения: 09.03.2025).
6. <i>Zhi X., Li W., Fan F.,</i> [et al.]. Influence of initial geometric imperfection on static stability of single-layer reticulated shell structure. Spatial Structures. 2021;27:7. (In Chinese). https://doi.org/10.13849/j.issn.1006-6578.2021.01.009.
7. <i>Li H., Wang C., Han J.</i> Research on Effect of Random Initial Imperfections on Bearing Capacity of Single-Layer Spherical Reticulated Shell. Industrial Construction. 2018;48:23–27. (In Chinese).
8. <i>Liu H., Zhang W., Yuan H.</i> Structural stability analysis of single-layer reticulated shells with stochastic imperfections. Engineering Structures. 2016;124:473–479. https://doi.org/10.1016/j.engstruct.2016.06.046.
9. <i>Xin T., Zhao J., Cui C., Duan Y.</i> A non probabilistic time variant method for structural reliability analysis. Proceedings of the Institution of Mechanical Engineers. Part O: Journal of Risk and Reliability. 2020;234(5):664–675. https://doi.org/10.1177/1748006X20928196.
10. <i>Yang M., Zhang D., Han X.</i> New efficient and robust method for structural reliability analysis and its application in reliability_based design optimization. Computer Methods in Applied Mechanics and Engineering. 2020;366:113018. https://doi.org/10.1016/j.cma.2020.113018.
11. <i>Fu X., Li H.-N., Li G., Dong Z.-Q., Zhao M.</i> Failure Analysis of a Transmission Line Considering the Joint Probability Distribution of Wind Speed and Rain Intensity. Engineering Structures. 2021;233:111913. https://doi.org/10.1016/j.engstruct.2021.111913.
12. <i>Fu X., Wang J., Li H.-N., Li J.-X., Yang L.-D.</i> Full-scale Test and its Numerical Simulation of a Transmission tower under Extreme Wind Loads. Journal of Wind Engineering and Industrial Aerodynamics. 2019;190:119–133. https://doi.org/10.1016/j.jweia.2019.04.011.
13. Постановление Правительства РФ № 914 от 20 мая 2022 года «О внесении изменений в постановление Правительства Российской Федерации от 28 мая 2021 г. № 815 [интернет]. Режим доступа: http://government.ru/docs/all/141098.
14. Постановление Правительства РФ от 28 мая 2021 г. № 815 "Об утверждении перечня национальных стандартов и сводов правил (частей таких стандартов и сводов правил), в результате применения которых на обязательной основе обеспечивается соблюдение требований Федерального закона «Технический регламент о безопасности зданий и сооружений», и о признании утратившим силу постановления Правительства Российской Федерации от 4 июля 2020 г. № 985" [интернет]. Режим доступа: http://government.ru/docs/all/134485.
15. СП 20.13330.2016. Нагрузки и воздействия (с Изменениями № 1–4). Актуализированная редакция СНиП 2.01.07-85* [интернет]. Режим доступа: https://normativ.kontur.ru/document?moduleId=9&documentId=470938.
16. СП 28.13330.2017. Защита строительных конструкций от коррозии. Актуализированная редакция СНиП 2.03 (с Изменениями № 1–3) 11-85 [интернет]. Режим доступа: https://normativ.kontur.ru/document?moduleId=9&documentId=479525.
17. СП 131.13330.2020. Строительная климатология. Актуализированная редакция СНиП 23-01-99* (с Изменением № 1) [интернет]. Режим доступа: https://protect.gost.ru/document.aspx?control=7&baseC=101&RegNum=54&DocOnPageCount=15&page=5&id=239682.
18. СП 59.13330.2020. Доступность зданий и сооружений для маломобильных групп населения. Актуализированная редакция СНиП 35-01-2001 (с изменением № 1) [интернет]. Режим доступа: https://normativ.kontur.ru/document?moduleId=9&documentId=491916.
19. <i>Крупенина Д.С.</i> Надежность строительных конструкций на этапе проектирования. Молодой ученый. 2020;(14):93–94.
20. <i>Бармотин А.А., Дмитренко Е.А., Волков А.С., Машталер С.Н., Недорезов А.В., Казак К.А., Севостьянов Н.А.</i> Информационное моделирование при выполнении обследования зданий. Современное промышленное и гражданское строительство. 2024;20(2):93–109.
21. <i>Долганов А.В.</i> Оптимизация железобетонных сооружений и конструкций по критерию надежности [диссертация]. Москва; 2000.
22. <i>Rui X., Ji K., Li L., McClure G.</i> Dynamic Response of Overhead Transmission Lines with Eccentric Ice Deposits Following Shock Loads. IEEE Transactions on Power Delivery. 2017;32(3):1287–1294. https://doi.org/10.1109/TPWRD.2015.2501029.
23. <i>Сенькин Н.А., Филимонов А.С. </i>Взаимодействие конструктивных элементов в линейной цепи воздушной линии электропередачи. Жилищное строительство. 2024;(1-2):101–108. https://doi.org/10.31659/0044-4472-2024-1-2-101-108.
24. <i>Ведяков И.И., Еремеев П.Г., Одесский П.Д., Попов Н.А., Соловьев Д.В.</i> Расчет строительных конструкций на прогрессирующее обрушение: нормативные требования. Промышленное и гражданское строительство. 2019;(4):16–24. https://doi.org/10.33622/0869-7019.2019.04.16-24.
25. <i>Adam J.M., Parisi F., Sagaseta J., Lu X.</i> Research and practice on progressive collapse and robust ness of building structures in the 21st century. Engineering Structures. 2018;173:122–149. https://doi.org/10.1016/J.ENGSTRUCT.2018.06.082.
26. <i>Zheng L., Wang W., Li H.</i> Progressive collapse resistance of composite frame with concrete-filled steel tubular column under a penultimate column removal scenario. Journal of Constructional Steel Research. 2022;189:107085. https://doi.org/10.1016/J.JCSR.2021.107085.
27. <i>Перельмутер А.В., Криксунов Э.З., Мосина Н.В.</i> Реализация расчета монолитных жилых зданий на прогрессирующее (лавинообразное) обрушение в среде вычислительного комплекса «SCAD Office». Инженерно-строительный журнал. 2009;(2):13–18.
28. <i>Мущанов В.Ф., Оржеховский А.Н., Цепляев М.Н., Мущанов А.В.</i>. Комплексный подход к оценке надежности пространственных металлических конструкций. Строительство: наука и образование. 2024;14(1):6–23. https://doi.org/10.22227/2305-5502.2024.1.1.
29. <i>Мущанов В.Ф., Оржеховский А.Н., Кащенко М.П., Зубенко А.В.</i> Надежность пространственных стержневых конструкций усеченных большепролетных куполов. Металлические конструкции. 2023;29(1):47–61.
30. <i>Мущанов В.Ф., Оржеховский А.Н., Мущанов А.В., Цепляев М.Н.</i> Надежность пространственных стержневых металлических конструкций высокого уровня ответственности. Вестник МГСУ. 2024;19(5):763–777. https://doi.org/10.22227/1997-0935.2024.5.763-777.
31. <i>Миронов А.Н., Смирнова Н.С., Оленич Е.Н., Мущанов А.В.</i> Натурное освидетельствование арочных металлических конструкций покрытия спорткомплекса «Ильичевец», г. Мариуполь. Металлические конструкции. 2023;29(3):153–166.
Об авторах
В. А. КоротковРоссия
Владимир Анатольевич Коротков, канд. техн. наук, ведущий научный сотрудник отдела надежности строительных конструкций, ФБУ «НТЦ ЯРБ», Москва
ул. Малая Красносельская, д. 2/8, к. 5, г. Москва, 107140, Российская Федерация
e-mail: korotkov@secnrs.ru
П. А. Родин
Россия
Павел Александрович Родин*, научный сотрудник отдела надежности строительных конструкций, ФБУ «НТЦ ЯРБ», Москва
ул. Малая Красносельская, д. 2/8, к. 5, г. Москва, 107140, Российская Федерация
e-mail: prodin@secnrs.ru
Рецензия
Для цитирования:
Коротков В.А., Родин П.А. Определение критического значения частоты собственных колебаний и модуля деформации железобетонных строительных конструкций для динамического мониторинга. Вестник НИЦ «Строительство». 2025;46(3):62-74. https://doi.org/10.37538/2224-9494-2025-3(46)-62-74. EDN: IYVTTR
For citation:
Korotkov V.A., Rodin P.A. Calculating the critical value of the natural frequency and deformation modulus of reinforced concrete structures for dynamic monitoring. Bulletin of Science and Research Center of Construction. 2025;46(3):62-74. (In Russ.) https://doi.org/10.37538/2224-9494-2025-3(46)-62-74. EDN: IYVTTR


























